基于磁场梯度张量的拉索断丝监测方法

江胜华，孙伟贺

·农业生物环境与能源工程·

基于磁场梯度张量的拉索断丝监测方法

江胜华1,2，孙伟贺1

（1. 西南大学工程技术学院 重庆 400715；2. 大连理工大学土木工程学院 大连 116024）

针对目前兴起的拉索损伤磁记忆检测方法易受环境干扰磁场影响的问题，该研究基于磁场梯度张量和磁荷面积分理论研究温室拉索断丝监测方法，推导拉索钢丝的磁场梯度计算公式，提出拉索断丝位置和断丝数量的判定方法，并采用磁场试验进行对比验证。为了验证试验的可重复性，对于每一种测试工况均设定了2组试验。理论计算表明，3个方向的磁感应强度沿拉索长度方向的磁场梯度（B，B和B）曲线均在断丝位置（500 mm）出现突变，一束拉索中断丝2根与断丝1根时3个磁场梯度曲线突变处包围的面积的比值的平均值约为2。磁场试验结果表明，断丝位置为496 mm，与实际断丝位置（500 mm）的误差为0.8%，通过2次测量，一束拉索中断丝2根与断丝1根时3个磁场梯度曲线突变处包围的面积的比值的平均值约为2。2次测量结果的差别极小，验证了试验的可重复性和可靠性。实际工程中，取3个磁场梯度判断的断丝数量的平均值，可以有效减小三轴磁传感器探头位置带来的误差。该研究为拉索断丝监测提供了理论依据，且有效排除了环境磁场干扰。

温室；断丝；监测；磁场梯度张量；断丝位置；断丝数量

0 引 言

随着农业现代化、专业化和集约化的发展，传统节能日光温室的建设成本高，土地利用率低，室内空间小，机械化作业不便等缺点逐渐凸显[1-2]。为改善这些问题，提高温室空间的整体利用效率以及日光温室结构的机械化程度，日光温室逐渐向着大跨度大体量方向发展，由最早6～7 m的小跨度，已达到10 m多甚至20 m[3]。而大风、暴雪等偶然荷载对日光温室结构的安全影响极大，在极端天气影响下，大跨度日光温室经常发生倒塌事件，造成巨大财产损失及人员伤亡。而日光温室大棚倒塌的主要原因可归结为骨架或者承重墙失效[4]。在实际生产中，为确保大跨度温室结构在风雪等极端恶劣天气下的安全，通常采用跨间增加支撑的方式提高结构的承载能力和安全性能。但是盲目增加支撑会降低结构温室内部的有效空间，不利于日常生产使用[5]。为同时满足温室的力学性能及使用功能，抗风拉索、预应力拉索等拉索构件在温室中的应用也越来越多[3-4,6]，布置拉索可以大幅度提升原有结构的极限荷载[7]。

以拉索作为主要承载构件的大跨度温室，在长期荷载与环境的共同影响下，拉索内部的钢丝断裂是最频繁、最严重的病害，拉索断丝直接关系到温室结构的安全和剩余寿命，因此，需要进行大跨度温室结构的拉索断丝检测与监测。现阶段，拉索断丝监测方法主要分为人工检测法、超声导波检测、红外热成像检测、光学检测、模态分析法及近些年新兴的电磁检测法。传统的人工检测法效率低下，精准度较低，并且测量人员需要高空作业，消耗大量人力物力且严重威胁操作人员的安全。超声导波检测法依据导波在断丝处产生的回波来检测断丝，但是超声导波在应用中通常需要噪声分析及降噪处理，虽精度较高但是无法探测细小损伤且操作繁琐[8-10]。红外热成像检测法通过比较缺陷处与完好拉索的温度差来判断损伤，该方法受环境温度影响较大[11-12]。近年来，随着光学检测方法发展，基于灰度图像处理和模式识别的实时监测方法可以准确、迅速地识别损伤，但仅能监测无护套的索体[13-14]。模态分析法通过分析拉索的模态参数等动力特性检测拉索断丝，但精度较低[15-17]。

最近十年来出现的电磁检测方法主要包括：涡流检测（Eddy Current Testing，ECT）[18-20]、漏磁检测（Magnetic Flux Leakage，MFL）[21-25]及金属磁记忆检测（Metal Magnetic Memory，MMM）[26-28]。涡流检测法首先对拉索励磁，拉索表面及附近出现感生涡流，而感生涡流产生的磁场将会反作用于检测线圈，进而得到涡流检测信号，在拉索断丝处感应涡流和磁场会发生变化。漏磁检测法的依据是，断丝部位磁导率会发生变化，拉索内部磁信号会在断丝处泄漏到空气中，从而对断丝进行检测。涡流检测法和漏磁检测法是现阶段应用较多的无损检测技术，但需要事先使用其他手段判断拉索断丝的大致位置，然后对断丝部位进行励磁处理后监测断丝数量。也有学者沿着整个拉索长度上励磁，同时监测断丝位置和断丝数量。常规磁记忆检测法根据磁性体本身的磁感应强度信号在断丝位置的突变，来检测拉索断丝，但没有消除包含地磁场在内的环境磁场的影响，导致误差较大。

磁源体的磁场梯度张量与其磁矩及位置直接相关，不受磁传感探头朝向影响，且磁源体的磁矩与其几何形状、边界条件及磁化强度直接相关，所以磁源体的磁场梯度受地磁场等环境干扰磁场的影响较小，可更好地描述磁源体的边界、位置以及磁化形态等，提高了探测效率和探测精度[29-30]。

由于磁场梯度张量包含磁性体更多的信息，受环境磁场的影响小，且与磁源体的几何形态直接相关，而拉索断丝后其几何形态发生改变。本文结合磁场梯度张量和磁荷面积分理论推导拉索钢丝的磁场梯度计算公式，给出拉索钢丝断丝时的特征信息，提出拉索断丝位置和断丝数量的判断方法，并采用磁场试验进行验证。

1 基于磁场梯度的拉索断丝监测

1.1 磁场梯度计算

以单根拉索钢丝为对象，拉索钢丝长度为(mm)，半径为(mm)，如图1所示。

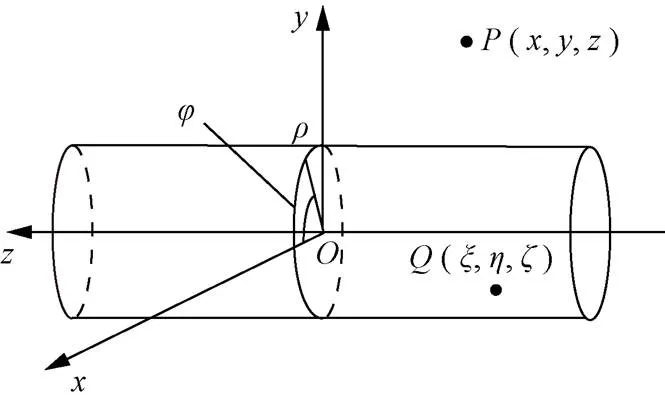
注：在笛卡尔坐标系Oxyz下，钢丝长度中部截面的圆心为坐标原点O，在水平面内且垂直于拉索长度方向为x轴，在铅锤面内且垂直于拉索长度方向为y轴，沿拉索钢丝长度方向为z轴。P (x, y, z)为磁传感器探头的测量位置，Q ( ξ, η, ζ)为拉索钢丝内任意一点。以原点O建立柱坐标系Oρφz。

在柱坐标系下，拉索钢丝沿长度方向轴的磁化强度为定值M(A/m)，沿径向方向的磁化强度在拉索长度的中部为0、在拉索两端的绝对值取最大值M(A/m)，在长度范围内呈线性变化，沿环向（方向）的磁化强度为0，则拉索钢丝的磁化强度为

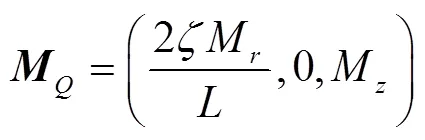
式中为磁化强度矢量，A/m。

将拉索钢丝的磁体元的磁位进行体积分求和，则一根拉索钢丝的磁位为[31]

式中为标量磁位，A。

根据散度公式和格林公式，式（2）可转化为

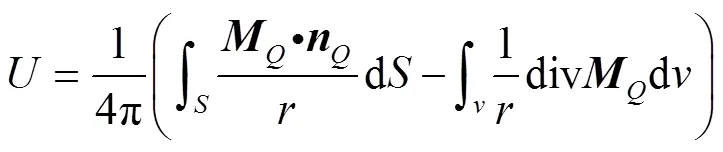
式中为测点到的距离，mm，为拉索钢丝表面的各面外法向方向的单位矢量。

拉索钢丝的磁位对磁位方向单位矢量求负导数，得到拉索钢丝磁感应强度矢量（nT）

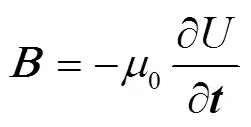
将式（3）代入式（4）可得

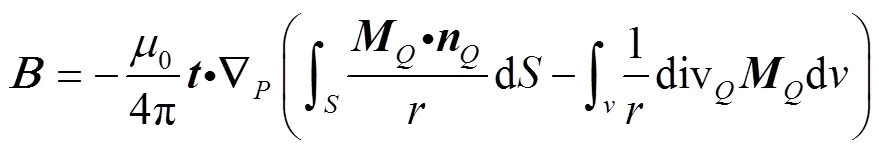
式中0为真空磁导率，0=4π×10-7T.m/A。

磁感应强度对求导，得到磁感应强度沿拉索钢丝长度方向（轴方向）的磁场梯度为

式（6）可展开为

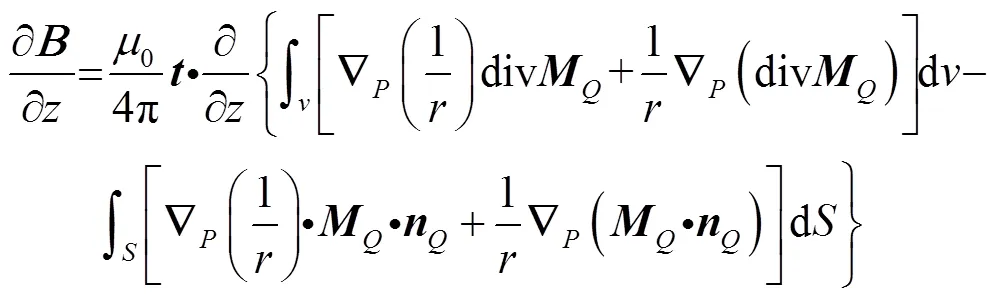
通过式（7）展开得到磁感应强度沿方向的磁场梯度、和（单位均为nT/mm）：

将式（8）～式（10）进一步展开得到：

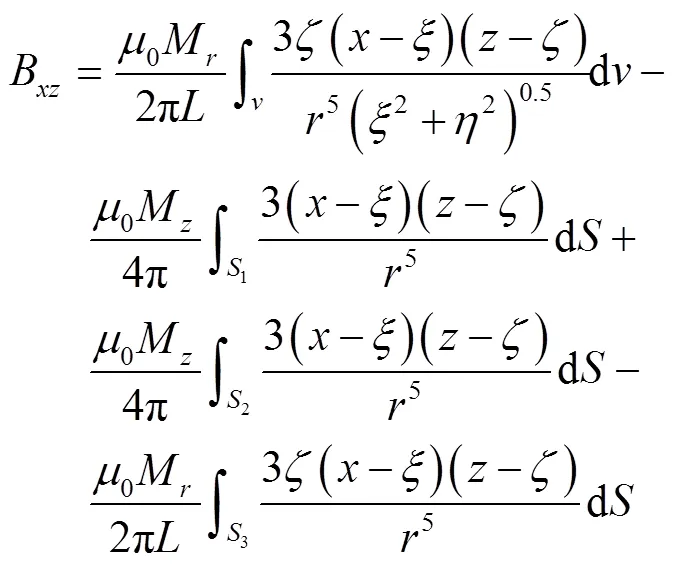
式中1、2、3分别为拉索钢丝的二个圆形端面和圆柱形侧面，其中，1和2的外法向方向的单位矢量分别为轴正向和负向。

一根钢丝断裂成为2根钢丝，其磁场梯度为2根断裂钢丝的磁场梯度的叠加，叠加的总磁场梯度在断丝处发生突变。在一束拉索钢丝中，若干钢丝断丝后，其磁场梯度视为未断丝的钢丝和断裂钢丝的磁场梯度的叠加。因此，可以根据断丝处磁场梯度突变的大小判断断丝位置和断丝数量。

1.2 磁场分析

一束（52根）直径为7 mm的热镀锌拉索钢丝，标准抗拉强度为1 570 MPa，排列方式如图2所示，拉索钢丝长度=1 000 mm，实测的磁化强度为M=40 040.435 A/m，M=2 870.756 A/m。在实际工程中，磁场传感器探头始终紧贴拉索表面，在拉索环向和长度方向2个方向移动；另一方面，拉索较长，磁场梯度曲线大部分平缓的中间部分，而两端磁场变化剧烈。因此，在理论分析及后续的试验中，选取靠近磁场传感器探头的24号和31号钢丝，断丝位置选择中间位置0.5处。根据式（11）～（13），可分别得到一束拉索钢丝无断丝的磁场梯度，一束拉索钢丝中1根断丝（31号，断丝位置为0.5处，即500 mm处）、2根断丝（24号和31号，断丝位置为500 mm处）的磁场梯度。完好的拉索与1根断丝、2根断丝的拉索的磁场梯度对比曲线如图2。

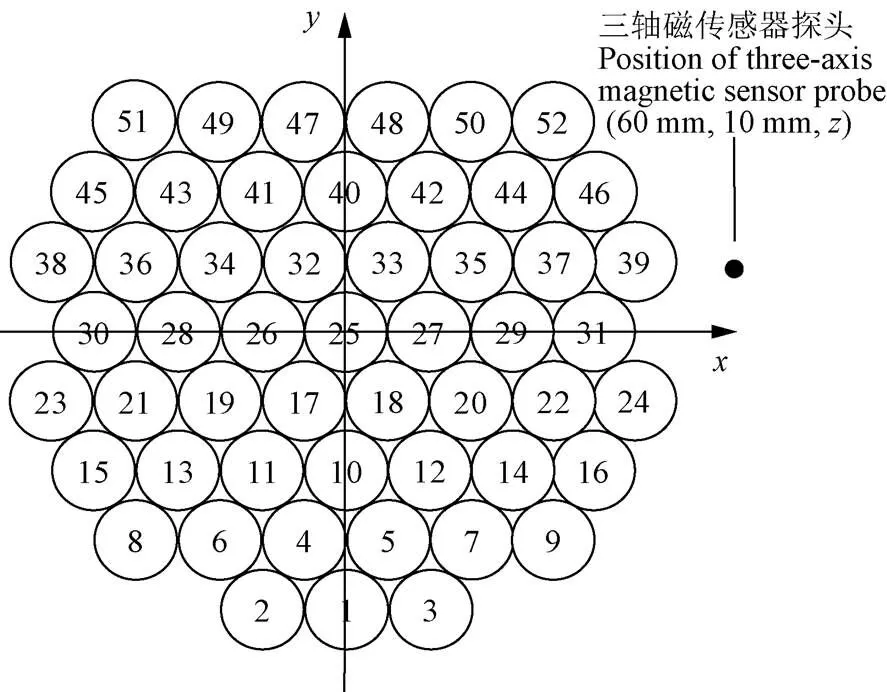
注：1～52为钢丝编号。

由图3可知，一束拉索钢丝无断丝时磁场梯度与曲线，呈平滑的M形，曲线呈平缓的N形。当一束拉索钢丝中出现断丝（24号和31号）时，拉索磁场梯度曲线在断丝位置出现较为明显的突变。具体而言，断丝位置（500 mm处）为磁场梯度、曲线波谷的谷底，曲线波峰与波谷之间的拐点。当一束拉索钢丝中断丝数量增加时，磁场梯度、和的突变形状一致，但突变幅度相应增大，即磁场梯度曲线在断丝处突变形成的波峰和波谷的深度增加，突变处包围的面积增加。

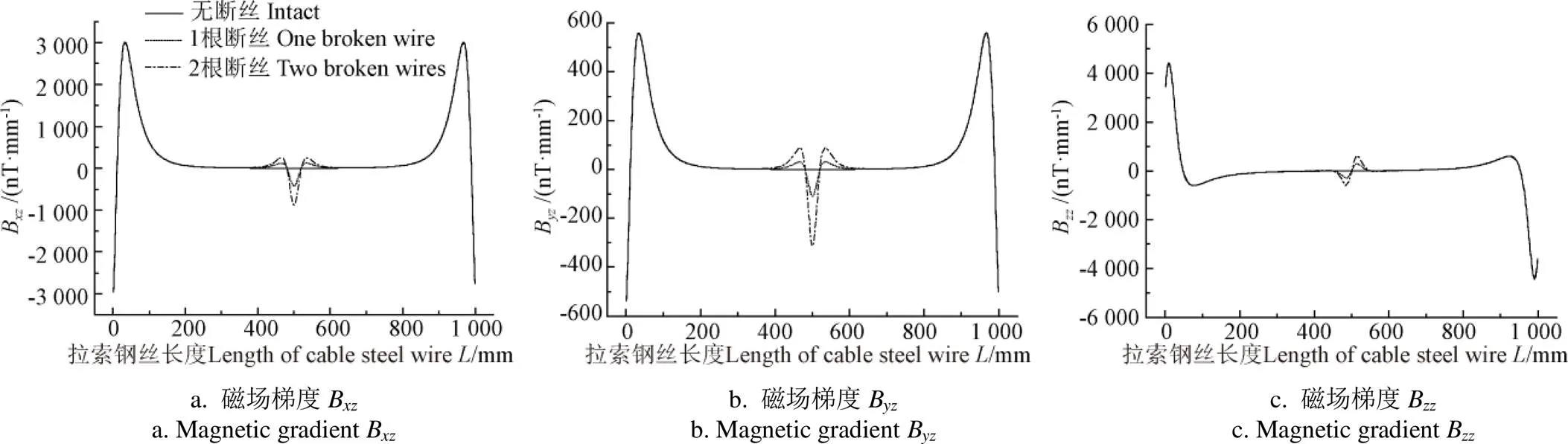
图3 一束拉索钢丝不同断丝数量时磁场梯度

磁场梯度与曲线突变处可近似为一个三角形；曲线突变处可近似为2个大小相同的三角形。、和曲线突变处包围的面积计算如下：

式中、分别为磁场梯度与曲线突变处波谷的宽度，mm，以突变处两个最高点的横轴距离为准；、分别为与曲线突变处波谷的深度，nT/mm，以波谷的谷底到突变处最高点的纵轴距离为准；为曲线波峰与波谷的宽度之和，mm；为曲线波峰与波谷的深度之和，nT/mm；、和分别为、和曲线突变处包围的面积，nT。

整束拉索（52根）中1根和2根断丝时，磁场梯度理论曲线在断丝处特征参数的比较见表1。

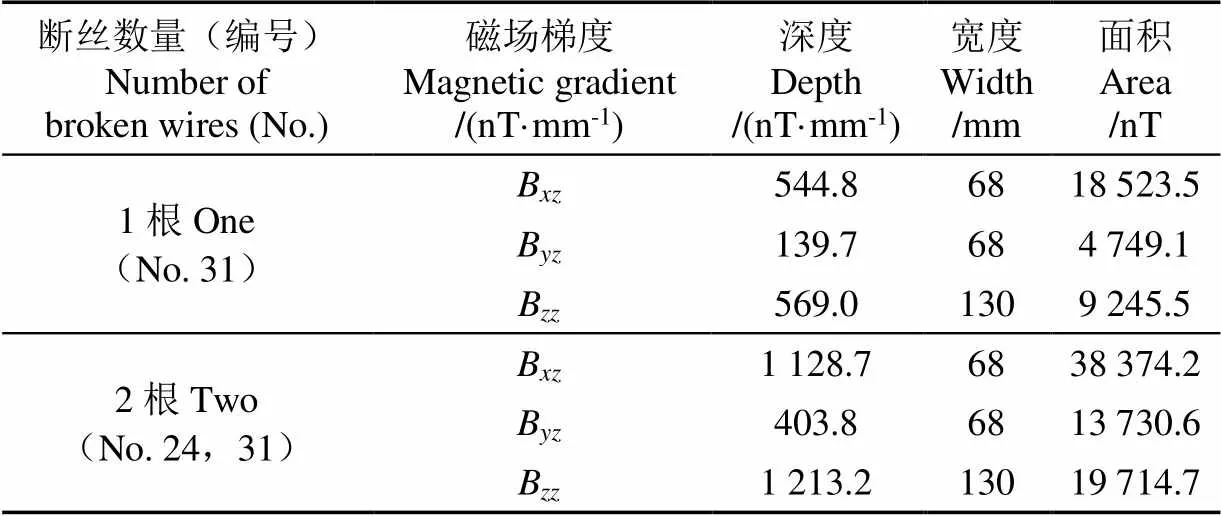
表1 断丝数量与磁场特征参数的关系（理论值）

一束拉索中1根（31号）断丝时，磁场梯度曲线、和突变处包围的面积分别为18 523.5、4 749.1和9 245.5 nT。一束拉索中2根（24号和31号）断丝时，磁场梯度曲线、和突变处包围的面积分别为38 374.2、1 3730.6和19 714.7 nT。2根断丝与1根断丝时三个磁场梯度曲线突变处包围的面积的比值分别为2.07、2.89和2.13，平均值为2.37。实际断丝监测时，此处突变处包围的面积的比值表示断丝数量的比值。以断丝1根时磁场梯度曲线突变处包围的面积为基准，比值2.37取整数为2，表示断丝为2根。

三轴磁传感器探头的测点坐标为（60 mm，10 mm，），在和轴方向，24号和31号钢丝与三轴磁传感探头的距离相差较小，而在轴方向，24号和31号钢丝距三轴磁传感探头的距离相差较大，导致2根（24号和31号）断丝时，24号和31号钢丝在测点处的磁场梯度和相差较小，而2根钢丝（24号和31号）在测点处的磁场梯度相差较大。因此，2根断丝与1根断丝时磁场梯度曲线突变处包围的面积的比值较大，且大于磁场梯度曲线和突变处包围的面积的比值，在实际工程中，为了考虑三轴磁传感器探头位置的影响，可取3个磁场梯度曲线突变处包围面积的平均值判断断丝数量。

随着拉索长度增加，磁场梯度曲线中间平缓部分的长度增加，但总体上，与曲线，呈平滑的M形，曲线呈平缓的N形，分布规律仍保持不变；磁场梯度曲线在断丝位置的突变幅度不会发生改变，拉索长度对突变幅度没有影响。本文通过突变的位置，进行断丝位置监测；通过突变处的深度和包围的面积来确定断丝数量。因此，拉索长度对断丝位置和断丝数量监测没有影响。

2 拉索断丝监测试验

2.1 试验装置与方法

2.1.1 试验装置

基于磁场梯度和磁荷面积分理论的拉索断丝监测试验系统包括磁场传感系统和运动控制系统，见图4。磁场传感系统包括三轴磁传感器探头、传输线、采集器、数据处理模块。磁场传感系统为德国DM050三轴磁通门磁力仪，量程为±1 000 000 nT，精度为0.002 nT。三轴磁传感器探头固定在铝合金延伸杆上，以排除电机和导轨的磁场干扰。菲林软尺承台为无磁装置，充分消除了试验装置自身的磁场干扰。拉索试件（与导轨平行，垂直于延伸杆）放置于菲林软尺承台上，紧贴磁传感器探头。三轴磁传感器探头沿拉索全长运动，采集拉索全长度的磁场信号。试验中拉索试件及相关参数与理论分析中相同。

图4 拉索断丝监测装置

2.1.2 试验方法

在菲林软尺承台上不放置拉索钢丝、处于空置状态，三轴磁传感探头扫描1 000 mm，得到环境磁场的磁感应强度（、、），并计算磁场梯度（、、）。

放置一束长度为1 000 mm的完好拉索钢丝（52根），扫描其长度范围内的磁感应强度，并计算磁场梯度。对于整束拉索，测得的磁场参数本质上为环境磁场和拉索磁场的叠加，即在整束拉索处，三轴磁传感探头直接测得的磁感应强度为环境磁场和拉索磁场叠加后的总磁感应强度，磁场梯度也为叠加后的总磁场梯度。

拉索断丝后，分别测量断丝1根（31号）和断丝2根（24号和31号）的整束拉索在其长度范围内的磁感应强度，并计算磁场梯度。为验证试验的准确性及可重复性，1根断丝和2根断丝的每种工况，均测量2次。

2.2 拉索断丝监测试验结果分析

2.2.1 环境磁场的影响

环境磁场和总磁场的磁场参数的变化范围及其长度范围内绝对值的平均值见表2。

由表2可知，在试验中，环境磁场的磁感应强度（、、）绝对值的平均值分别为37 131.0、13 178.7和29 144.0 nT；整束拉索和环境磁场叠加的总磁感应强度（、、）绝对值的平均值分别为259 117.4、87 165.7和121 184.2 nT。环境磁场的磁感应强度绝对值的平均值(|B|）、(|B|）和(|B|）分别占总磁感应强度的绝对值平均值的14.33%、15.12%、24.05%，且环境磁场的磁感应强度在长度范围内变化幅度较大。因此，当采用磁感应强度检测拉索断丝时，不可忽视环境磁场的影响，必须解决从总磁感应强度中分离环境磁感应强度的难题。

环境磁场的磁场梯度（、和）绝对值的平均值分别为2.04、3.38和1.39 nT/mm；整束拉索和环境磁场叠加的总磁场梯度（、和）绝对值的平均值分别为1 200.07、366.99和671.44 nT/mm。环境磁场的磁场梯度绝对值的平均值分别占总磁场梯度的0.17%、0.92%、0.21%，且环境磁场的磁场梯度在长度范围内变化幅度极小。因此，可以忽略环境磁场梯度的影响，认为测得的总磁场梯度等于拉索的磁场梯度，可采用磁场梯度为依据检测拉索断丝。

表2 环境磁场和总磁场的比较

2.2.2 断丝监测

一束拉索钢丝中1根断丝（31号）和2根断丝（31号和24号）的磁场梯度的两组曲线规律基本一致，仅给出1组试验结果，如图5。

由图5所示，磁场梯度和曲线波谷的谷底可得断丝位置分别为494和493 mm，zz曲线波峰与波谷之间的拐点可得到拉索断丝位置为495 mm，3个断丝位置的平均值为494 mm。2组试验断丝位置结果见表3。

图5 一束拉索钢丝中不同断丝数量时的磁场梯度

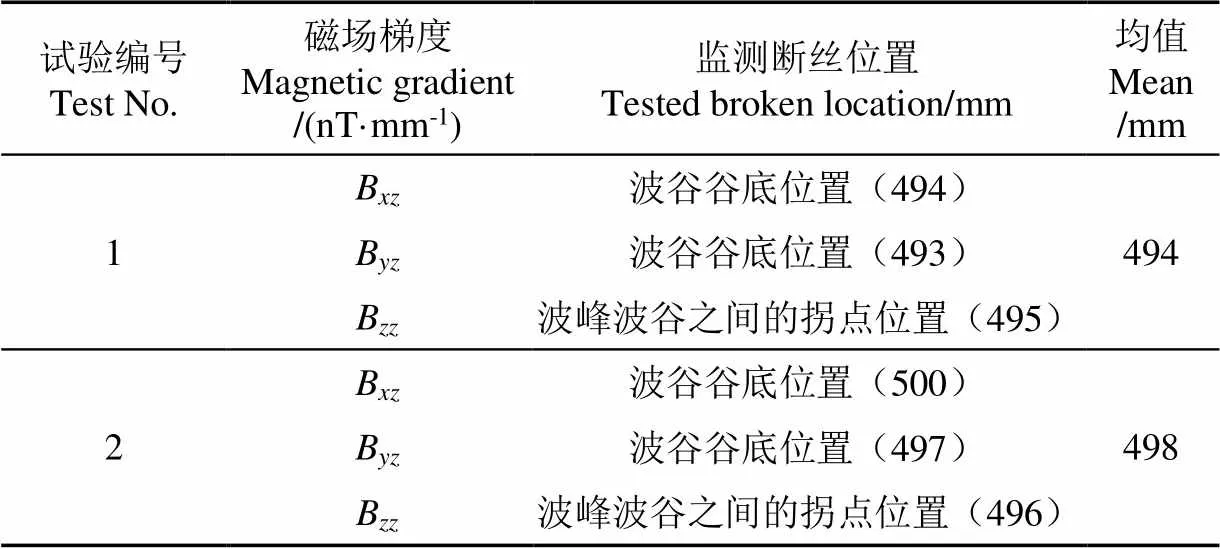
表3 拉索断丝位置判断

由表3可知，2组测量结果中，通过磁场梯度的突变判断得到的断丝位置分别为494和498 mm，与实际断丝位置500 mm相比，误差分别为1.2%、0.4%。2次试验的断丝位置测量结果的差别极小，验证了试验的可重复性和可靠性，测得的断丝位置的平均值为496 mm，与实际位置的误差为0.8%。

由图5的实测磁场梯度，分别计算1根断丝和2根断丝时的磁场梯度曲线中突变处波峰或波谷的深度、宽度及包围的面积，结果见表4。由表4可知，第1次试验中，一束拉索中1根（31号）断丝时，磁场梯度曲线、和突变处包围的面积分别为9 918.2、5 727.8和8 997.8 nT。一束拉索中2根（24号和31号）断丝时，磁场梯度曲线、和突变处包围的面积分别为14 610.8、10 173.2和12 015.0 nT。断丝2根与断丝1根时，磁场梯度曲线、和突变处包围的面积的比值分别为1.47、1.78和1.34，平均值为1.53。第2次试验中，2根断丝与1根断丝时，磁场梯度曲线、和突变处包围的面积的比值分别为1.48、1.84和1.31，平均值为1.54。2组试验取平均值，则断丝2根与断丝1根时，磁场梯度曲线、和突变处包围的面积的比值分别为1.48、1.81和1.33，平均值为1.54。以断丝1根时磁场梯度曲线突变处包围的面积为基准，比值1.54取整数为2，表示断丝为2根。2次试验的断丝数量测量结果的差别极小，验证了试验的可重复性和可靠性。

表4 磁场特征参数（实验值）与断丝数量的关系

在试验中，由于24号和31钢丝在轴方向与三轴磁传感器探头的距离相差较大，导致2根（24号和31号）断丝与1根（31号）断丝相比较时，磁场梯度曲线突变处包围的面积的比值较磁场梯度曲线和判断的比值大，与理论结果的规律相同。在实际工程中，建议3个方向的磁场梯度判断的断丝数量取平均值。

表4中，实测的2根断丝和1根断丝时磁场梯度突变处包围的面积的比值为1.54，表1中理论数据为2.37。以断丝1根时磁场梯度曲线突变处包围的面积为基准，比值均取整数为2，均表示断丝为2根，试验值和理论值判断的断丝数量一致。对于磁场梯度突变处包围的面积比值，理论计算值和试验测试值均与实际值（2.0）存在少许偏差，究其原因为：1）一束拉索包含52根钢丝，虽然出厂及施工时，通常情况下为同一批拉索钢丝，但每一根拉索钢丝的磁场特征存在少许的差别。而理论模型为偏于理想化的模型，假定每一根拉索钢丝的磁场特征完全相同。2）在试验中，由于拉索钢丝需要重复拆卸组装，没有组合成非常紧凑、密实的状态，导致和理论判断的断丝数量存在偏差。3）由于2根钢丝在轴和轴方向上与三轴磁传感器探头的距离并非相等，而钢丝与三轴磁传感器探头的距离直接影响磁场梯度的数值。

本文方法在监测断丝位置时，误差为0.8%，精度极高，在监测断丝数量时精度较高。对于拉索内部钢丝的断丝监测有待于进一步研究。

3 结 论

本文提出一种可有效排除环境磁场干扰的基于磁场梯度张量和磁荷面积分理论的拉索断丝监测方法。结合磁场梯度张量和磁荷面积分理论推导拉索钢丝的磁场梯度计算公式，提出拉索断丝位置和断丝数量的判定方法，并采用磁场试验进行对比验证，主要结论如下：

1）理论计算的磁场梯度曲线表明，当一束拉索中出现断丝时，磁场梯度曲线在断丝位置出现突变。磁场梯度曲线的拐点可作为判断断丝位置的依据。随着断丝数量的增加，根据叠加效应磁场梯度曲线断丝处突变形成的波峰和波谷的深度增加，突变处包围的面积增加。

2）试验中，磁场梯度曲线突变位置的平均值对应的断丝位置为496 mm，与实际断丝位置500 mm相比，误差为0.8%，断丝位置监测的精度极高。

3）由试验测得的磁场梯度曲线表明，一束拉索中2根断丝时，磁场梯度曲线、和突变处包围的面积与1根断丝时的比值的平均值，约等于2，与理论计算值判断的断丝数量一致。本文断丝监测方法可有效排除环境磁场干扰，断丝监测的精度较高。

[1] 鲍恩财，曹晏飞，邹志荣，等. 节能日光温室蓄热技术研究进展[J]. 农业工程学报，2018，34(6)：1-14.

Bao Encai, Cao Yanfei, Zou Zhirong, et al. Research progress of thermal storage technology in energy-saving solar greenhouse[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(6): 1-14. (in Chinese with English abstract)

[2] 徐航，李雄彦，徐开亮. 大型连栋温室的研究现状[J]. 建筑结构，2021，51(S2)：393-398.

Xu Hang, Li Xiongyan, Xu Kailiang. Research status and prospect of large multi-span greenhouse[J]. Building Structure, 2021, 51(S2): 393-398. (in Chinese with English abstract)

[3] 田兴运，何斌，朱雄伟. 日光温室结构优化现状与新思路探索[J]. 东北农业科学，2020，45(4)：58-62.

Tian Xingyun, He Bin, Zhu Xiongwei. Current situation and further discussion on the optimization of solar greenhouse structure[J]. Journal of Northeast Agricultural Sciences, 2020, 45(4): 58-62. (in Chinese with English abstract)

[4] 杨升华，刘雪迎，蒋秀根. 基于临时加固策略的日光温室极端风雪灾害对策[J]. 江苏大学学报(自然科学版)，2022，43(1)：45-53.

Yang Shenghua, Liu Xueying, Jiang Xiugen. Countermeasures against extreme wind and snow disasters to solar greenhouses based on temporary reinforcement[J]. Journal of Jiangsu University (Natural Science Edition), 2022, 43(1): 45-53. (in Chinese with English abstract)

[5] 齐飞，闫冬梅，魏晓明. 日光温室前屋面支撑位置对实腹式骨架安全性的影响[J]. 农业工程学报，2020，36(16)：174-181.

Qi Fei, Yan Dongmei, Wei Xiaoming. Influences of south roof support position change on the skeleton structure safety in solid belly solar greenhouse[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(16): 174-181. (in Chinese with English abstract)

[6] 白义奎，佟国红，姜传军，等. 预应力拉索拱结构在日光温室骨架设计中的应用[J]. 钢结构，2002(3)：14-15.

Bai Yikui, Tong Guohong, Jiang Chuanjun, et al. Application of prestressing arch structure with pulling cable in skeleton designing of solar greenhouse[J]. Steel Construction, 2002(3): 14-15. (in Chinese with English abstract)

[7] 张中昊，付强，范峰. 拉索加强式温室单层球面网壳稳定性分析[J]. 农业工程学报，2017，33(22)：233-240.

Zhang Zhonghao, Fu Qiang, Fan Feng. Stability analysis of cable-stiffened single-layer two-way grid reticulated domes of greenhouse[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(22): 233-240. (in Chinese with English abstract)

[8] Bang S S, Lee Y H, Shin Y J. Defect detection in pipelines via guided wave-based time–frequency-domain reflectometry[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70, 9505811

[9] Wu J, Cai J H, Wang Y, et al. Detection of arbitrary frequency ultrasonic guided wave signals based on the Time-Shift duffing oscillator[J]. IEEE Access, 2021, 9: 95823-95831.

[10] Xu Z D, Zhu C, Shao L W, et al. Damage identification of pipeline based on ultrasonic guided wave and wavelet denoising[J]. Journal of Pipeline Systems Engineering and Practice, 2021, 12(4): 04021051.

[11] Lu S L, Zhang J W. Quantitative nondestructive testing of wire ropes based on features fusion of magnetic image and infrared image[J]. Shock and Vibration, 2019, 2019: 2041401.

[12] 马晔，邹露鹏，张理轻. 无人机加载光学摄像及红外成像系统对海上特大桥塔索质量检测的运用技术[J]. 公路交通科技，2018，35(8)：89-93，105.

Ma Ye, Zou Lupeng, Zhang Liqing. Application technology of UAV equipped with optical camera and Digital infrared imagery in inspecting quality of pylon and stay cable of sea-crossing bridge[J]. Journal of Highway and Transportation Research and Development, 2018, 35(8): 89-93, 105. (in Chinese with English abstract)

[13] Zhou P, Zhou G B, He Z Z, et al. A novel texture-based damage detection method for wire ropes[J]. Measurement, 2019, 148: 106954.

[14] Yaman O, Karakose M. Auto correlation based elevator rope monitoring and fault detection approach with image processing[C]// 2017 International Artificial Intelligence and Data Processing Symposium (IDAP), Malatya, Turkey, IEEE, 2017: 1-5.

[15] Ni Y C, Alamdari M M, Ye X W. Fast operational modal analysis of a single-tower cable-stayed bridge by a Bayesian method[J]. Measurement, 2021, 174: 109048.

[16] 刘菁，梁栋. 拉索-惯质阻尼器体系减振分析[J]. 重庆交通大学学报(自然科学版)，2022，41(1)：76-83.

Liu Jing, Liang Dong. Damping analysis of cable-inertial damper system[J]. Journal of Chongqing Jiaotong University (Natural Science), 2022, 41(1): 76-83. (in Chinese with English abstract)

[17] 孙利民，狄方殿，陈林，等. 斜拉索-双阻尼器系统多模态减振理论与试验研究[J]. 同济大学学报(自然科学版)，2021，49(7)：975-985.

Sun Limin, Di Fangdian, Chen Lin, et al. Theoretical and experimental studies on multimode vibration mitigation of cable with two dampers[J]. Journal of Tongji University(Natural Science). 2021, 49(7): 975-985. (in Chinese with English abstract)

[18] 于小杰，李旭东，解社娟，等. 钢丝绳断丝缺陷涡流检测方法[J]. 中国机械工程，2019，30(22)：2757-2763.

Yu Xiaojie, Li Xudong, Xie Shejuan, et al. ECT method for wire breakage defects in wire ropes[J]. China Mechanical Engineering, 2019, 30(22): 2757-2763. (in Chinese with English abstract)

[19] Bernieri A, Betta G, Ferrigno L, et al. Multifrequency excitation and support vector machine regressor for ECT defect characterization[J]. IEEE Transaction on Instrumentation and Measurement, 2014, 63(5): 1272-1280.

[20] Kiselev E K, Gol’dshtein A E. Eddy-current system for testing inner diameter of pipes[J]. Russian Journal of Nondestructive Testing, 2019, 55(3): 210-216.

[21] Liu S W, Sun Y H, Gu M, et al. Review and analysis of three representative electromagnetic NDT methods[J]. Insight, 2017, 59(4): 176-183.

[22] Zhang J W, Peng F C, Chen J B. Quantitative detection of wire rope based on three-dimensional magnetic flux leakage color imaging technology[J]. IEEE Access, 2020, 8: 104165-104174.

[23] 辛荣亚，张启伟. 基于漏磁检测的桥梁拉索钢丝损伤评估[J]. 桥梁建设，2019，49(3)：51-56.

Xin Rongya, Zhang Qiwei. Assessment of steel wire damages in bridge cables based on magnetic Flux leakage examination[J]. Bridge Construction, 2019, 49(3): 51-56. (in Chinese with English abstract)

[24] 王翔. 桥梁拉索内部断丝电磁探测技术研究[J]. 桥梁建设，2020，50(6)：27-32.

Wang Xiang. Research on using electromagnetic detection technology to identify broken wires in bridge cables[J]. Bridge Construction, 2020, 50(6): 27-32. (in Chinese with English abstract)

[25] Ni Y C, Zhang Q W, Xin R Y. Magnetic flux detection and identification of bridge cable metal area loss damage[J]. Measurement, 2021, 167: 108443.

[26] Chen H L, Wang C L, Zuo X Z. Research on methods of defect classification based on metal magnetic memory[J]. NDT and E International, 2017, 92: 82-87.

[27] Villegas-Saucillo J J, Díaz-Carmona J J, Cerón-Álvarez C A, et al. Measurement system of metal magnetic memory method signals around rectangular defects of a ferromagnetic pipe[J]. Applied Sciences, 2019, 9: 2695.

[28] Xia R C, Zhou J T, Zhang H, et al. Experimental study on corrosion of unstressed steel strand based on metal magnetic memory[J]. KSCE Journal of Civil Engineering, 2019, 23: 1320-1329.

[29] 江胜华，侯建国，何英明. 基于磁场梯度张量局部模量的钢筋锈蚀监测方法[J]. 西南交通大学学报，2021，56(6)：1176-1184.

Jiang Shenghua, Hou Jianguo, He Yingming. Steel corrosion monitoring based on partial modulus of magnetic gradient tensor[J]. Journal of Southwest Jiaotong University, 2021, 56(6): 1176-1184. (in Chinese with English abstract)

[30] 江胜华，侯建国，何英明，等. 基于磁偶极子的磁场梯度张量局部缩并及试验验证[J]. 中国惯性技术学报，2017，25(4)：473-477.

Jiang Shenghua, Hou Jianguo, He Yingming, et al. Theoretical study and experimental verification of magnetic gradient tensor partial contraction using magnetic dipole[J]. Journal of Chinese Inertial Technology, 2017, 25(4): 473-477. (in Chinese with English abstract)

[31] 管志宁. 地磁场与磁力勘探[M]. 北京：地质出版社，2005.

Cable wire breakage monitoring method using magnetic gradient tensor

Jiang Shenghua1,2, Sun Weihe1

(1.,,, 400715,; 2.,,116024,)

A safety risk has often posed a great threat to large-span greenhouse structures with the cables in extreme weather, such as snow and wind. It is very necessary to detect the broken wires in the cables of large-span greenhouse structures. However, the environmental magnetic field can dominate the magnetic memory detection for cable damage. In this study, an effective detection was presented for the broken wires using magnetic gradient tensor and magnetic charge surface integral theory, in order to remove the influence of the environmental magnetic field. The magnetic gradient tensor was then combined with the magnetic charge surface integral to derive the calculation formula for the magnetic gradient of cable wires. The characteristic information of cable wires was given before and after the wires broke. The judgment was also proposed for the wire breakage position and number of broken wires. The magnetic test was carried out to verify the evaluation. Theoretical calculation results show that there was a sudden change in the magnetic gradient curve at the wire breakage position when a broken wire occurred in a cable. As such, the baseline was established for the position of wire breakage using the bottom of the trough and the inflection point between the peak and trough of the magnetic gradient curve. Once there were two broken wires in a cable, the areas enclosed by the abrupt changes of magnetic gradient curves were 2.07, 2.89, and 2.13 times those in one broken wire, with an average value of 2.37, according to theoretical calculation. There was no effect of the cable length on the amplitude of mutation in the magnetic gradient curve. The average values of the environmental magnetic gradient’s absolute values account for 0.17%, 0.92% and 0.21% of the total magnetic gradient respectively. The influence of the environmental magnetic gradient can be ignored and it can be considered that the measured total magnetic gradient is equal to the cable’s own magnetic gradient. The experimental results show that the theoretical and actual wire breakage positions were 496, and 500 mm, respectively, with an error of 0.8%, in terms of the average value of abrupt changes in the magnetic gradient curves. There was a great increase in the areas and peaks/troughs depths that were surrounded by the abrupt changes of magnetic gradient curves, as the number of broken wires increased, according to the superposition effect. In order to verify the repeatability of the experiment, measurement was conducted twice for each wire-breaking condition. As for the first test results, the areas surrounded by the abrupt changes of magnetic gradient curves in the two broken wires were 1.47, 1.78, and 1.34 times those in the one broken, with an average value of 1.53. As for the second test results, the area ratios were 1.48, 1.84, and 1.31, with an average value of 1.54. The very small deviation between the results of the two measurements verified the repeatability and reliability of the monitoring. Anyway, the number of broken wires should be judged by three magnetic gradients in the practical engineering application. This finding can provide a theoretical basis for cable wire breakage monitoring, and effectively eliminate the interference of the environmental magnetic field.

greenhouse; wire breakages; monitoring; magnetic gradient tensor; location of wire breakage; number of broken wires

10.11975/j.issn.1002-6819.2022.22.015

TM153

A

1002-6819(2022)-22-0141-08

江胜华，孙伟贺.基于磁场梯度张量的拉索断丝监测方法[J]. 农业工程学报，2022，38(22)：141-148.doi：10.11975/j.issn.1002-6819.2022.22.015 http://www.tcsae.org

Jiang Shenghua, Sun Weihe. Cable wire breakage monitoring method using magnetic gradient tensor[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(22): 141-148. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2022.22.015 http://www.tcsae.org

2022-04-28

2022-10-21

国家自然科学基金项目（51208078）；重庆市基础与前沿研究计划（cstc2015jcyjA30008）；重庆市技术创新与应用示范（社会民生类）项目（cstc2018jscx-msybX0028）

江胜华，博士，副教授，研究方向为基于磁场的结构健康监测等方面。Email：jiangsh@whu.edu.cn