基于ARIMA 模型的民航旅客运输量预测
2022-03-09李黎莎
李黎莎
(中国民用航空飞行学院民航监察员培训学院,四川 广汉 618307)
民航旅客运输量是反应我国航空公司、机场运行效率的重要指标,同时也反应了我国旅客出行的需求情况和先关企业经营管理水平,科学准确地对旅客运输量进行预测和分析能有利于对航空公司、机场等民航运行单位的保障能力配备及运力投放提供决策支持。目前,对交通运输领域的预测主要集中在公里、铁路等交通量、短时交通流、票价方面。童名荣等[1]在ARIMA 的基础上通过对比分析,推导出预测精度更高的具有周期的季节性ARI-MA 模型;李万等[2]将相关性分析得到的铁路营业里程、国家铁路客车拥有量、国内生产总值和年末总人口作为铁路客运量的影响因素并对铁路客运量进行预测,提出改进粒子群算法(IPSO)和将粒子群算法(PSO)与长短时记忆神经网络相结合的预测模型。在民航领域中也对航班延误量、机场运输量、空管保障架次、平台旅客订票需求等多方面进行了预测研究。丁松滨等[3]采用SARIMA-LSTM 模型对民航各类飞行保障架次的时间序列进行预测,验证了此预测模型对民航空管系统各单位保障架次有较好的预测效果;蔡文婷等[4]通过对民航运输客运量历史数据对所构建多元回归模型的预测值进行比较分析,验证了多元回归模型的预测值与历史数据的相对误差较小、预测精度较高。本文利用民航局2007 年1 月至2019 年6 月的连续序列建立了基于ARIMA 的预测模型,留用2019 年下半年运输量数据用于验证模型的准确性,并对民航旅客运输量进行分析预测。
1 民航旅客运输量概况
根据中国民用航空局月度旅客运输量统计数据[4],历年民航旅客运输量(2007.1-2019.12)。以年为x 轴,对应的月度旅客运输量为y 轴,单位为万人次,绘制时序图,如图1。
由图1 可知,2007-2019 年旅客运输量总体呈上升趋势,从2007 年1 月的月度旅客运输量1241.7 万人次,2019 年12 月达到5276 万人次,是初始数据月的4.25 倍。对比民航行业的建设发展情况:2007 年,北京首都机场扩建,民航运输机场数量为152 个,在册航空器1134 架。2019 年,北京大兴机场投入使用,民用运输机场数量达到238 个,是2007 年的1.57 倍;民航全行业运输飞机期末在册航空器3818 架,比上年底增加179架,是2007 年的3.36 倍。民航旅客运输量主要受我国国民经济发展水平、居民收入水平、机场建设水平及服务能力等方面因素的影响。从以上数据可以看出,旅客运输量的增速和民航行业建设发展情况一致。故对民航旅客运输量数据的预测和分析有助于把握民航发展趋势,为各民航单位合理安排新增运力、完善运行战略规划等具有重要指导意义。

图1 2007-2021 年民航旅客运输量时序图
根据时序图的规律性变化还可以看出,年度内旅客运输量保持有规律的季节性波动,年变化趋势基本呈现相同规律。民航旅客运输量在每年2 月和7-8 月受春运、暑运影响,处于一年中运量最大值;在春运、暑运后出行人次显著降低。
2 ARIMA 模型介绍
2.1 ARIMA 模型
差分自回归平移模型(Autoregressive Integrated Moving Average, ARIMA)模型是一种有效的时间序列预测模型,是20 世纪60 年代有美国学者Box 和英国学者Jenkins 提出的。如使用ARIMA 模型分析的时间序列具有趋势,则对其作差分后变为平稳随机序列,再用平稳时间序列去建立描述这一随机过程的模型。最后,运用最佳拟合的模型,过去、现在的时间序列观测值对未来数据进行预测[1]。ARIMA(p,d,q)中,自回归模型AR,p 为自回归项数;移动平均模型MA 为滑动平均,q 为滑动平均项数,d 为使之成为平稳序列所做的差分次数,即阶数。ARIMA(p,d,q)的模型为

式中:y(t)为时间t 的旅客运输量;λ(B)为自回归算子;d 为差分次数;B 为延迟算子;θ(B)=1-θ1B-θ2B2-,…,θqBq 为移动平滑系数多项式(q 为移动平均阶数);εt为零均值白噪声序列。
2.2 数据来源
本文以2007-2019 年旅客运输量为基础数据序列,数据来源于中国民用航空局年度民航行业发展统计公报和月度运输生产指标统计[4]。
2.3 建立模型
采用SPSS 统计分析软件, 建立了ARIMA预测模型,原始序列为连续139 个月的民航旅客运输量,以万人次为单位。由图2 原始序列的自相关(ACF)图可知原始序列是非平稳的,根据图3 原始序列偏自相关(PACF)图可知需对原始旅客运输量序列进行差分,将原始序列进行预处理使其变为平稳的时间序列,见图4-5。
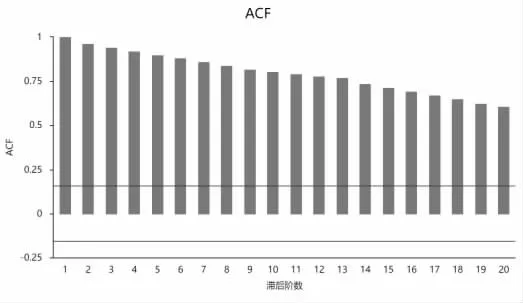
图2 原始序列自相关图

图3 原始序列偏自相关图

图4 差分序列自相关图
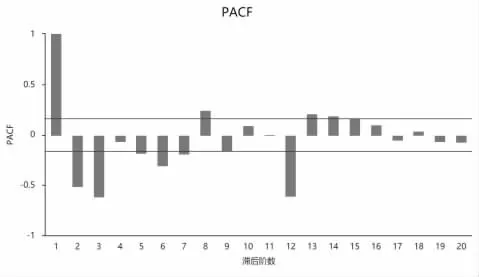
图5 差分序列偏自相关图
对于ARIMA 模型,若自相关函数在滞后数为p 后截尾和偏相关函数在滞后数为q 后截尾,则阶数分别为p 和q。利用SPSS 反复计算尝试后,基于最小信息量(AIC)原则,选择ARIMA(3,1,3)作为原始序列的最优模型,即p=3,d=1,q=3,其模型的其他参数如表1 所示。
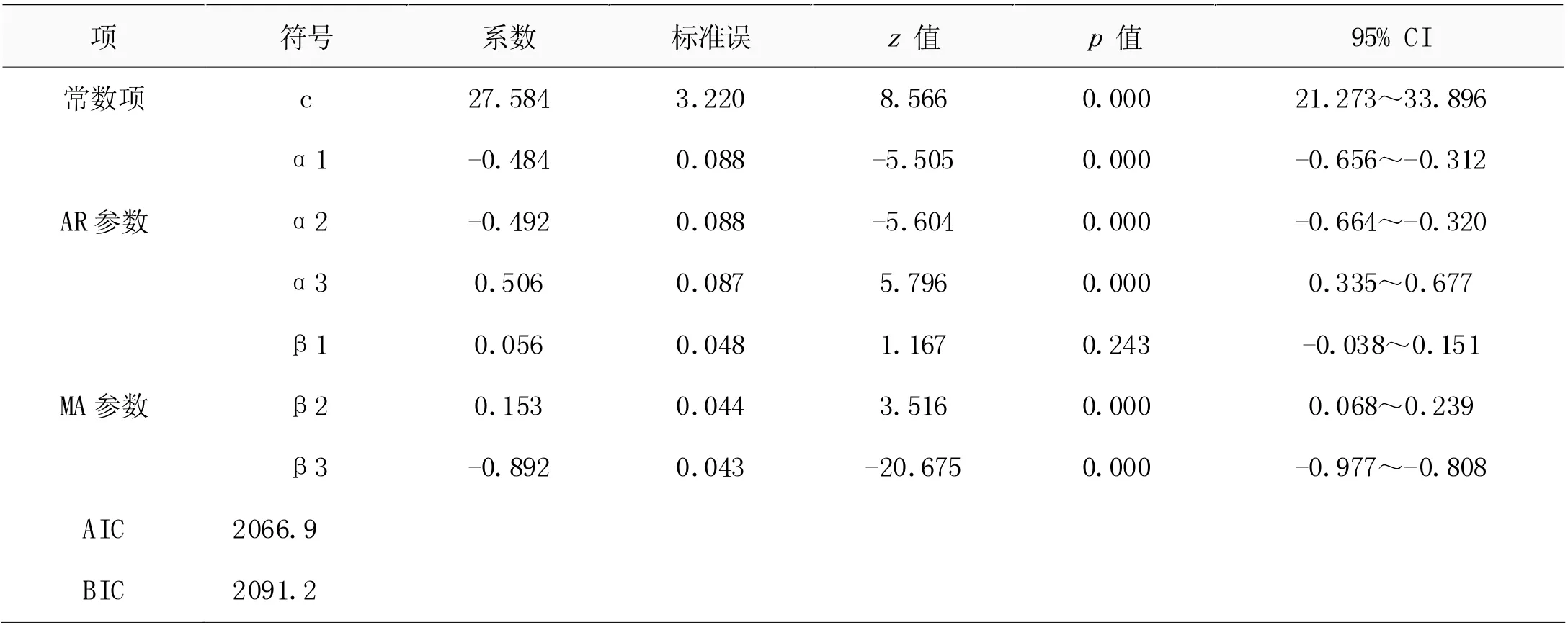
表1 旅客运输量预测ARIMA(3,1,3)模型参数表
模型在残差检验中P=0.614>0.05,满足残差的白噪声检验,不存在残差的自相关性,验证了该预测模型是可靠的,见表2。所以,可得出最优ARIMA 模型公式为:
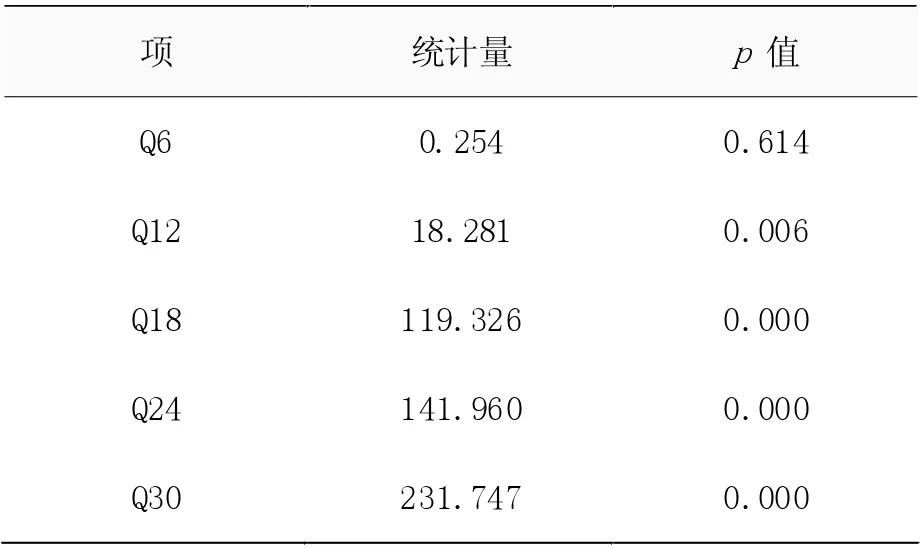
表2 模型Q 统计量表格
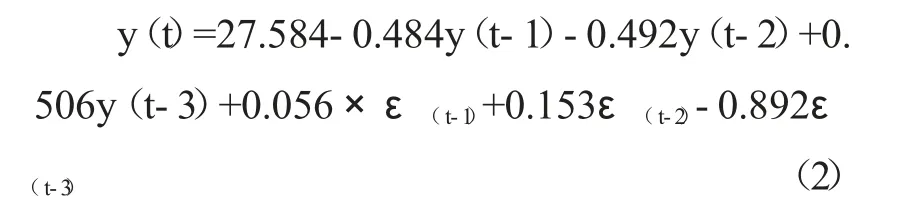
2.4 旅客运输量预测与验证
使用该模型进行旅客运输量预测,图6 为该最优预测模型ARIMA (3,1,3) 的拟合值与2007-2019 年真实数据的对比,由图可见该模型拟合良好。
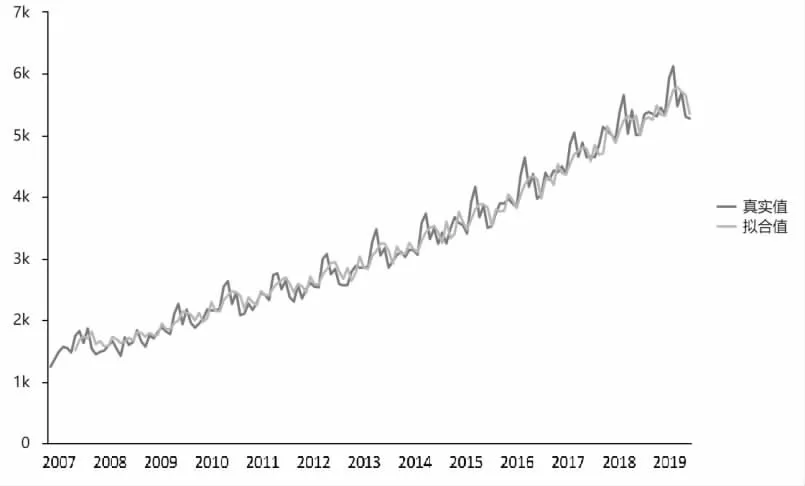
图6 2007-2019 年旅客运输量拟合
使用2019 年8 月-12 月的实际旅客运输量数据对该预测模型进行验证,误差值分别为1.22%、0.85%、0.92%、1.37%、1.36%,如表3。较小的预测误差值表明该模型的预测结果准确、预测精度较好,可用于后续民航旅客运输量的分析研究。在利用模型对2020 年12 个月的旅客运输量进行预测数据,结果如表4。由2020 年的预测结果可见,最大旅客运输量仍出现在元旦、春节及暑假期间,在节后呈现下降趋势,其波动情况与历史数据一致。

表3 2019 年8-12 月旅客运输量预测值与真实值的误差分析
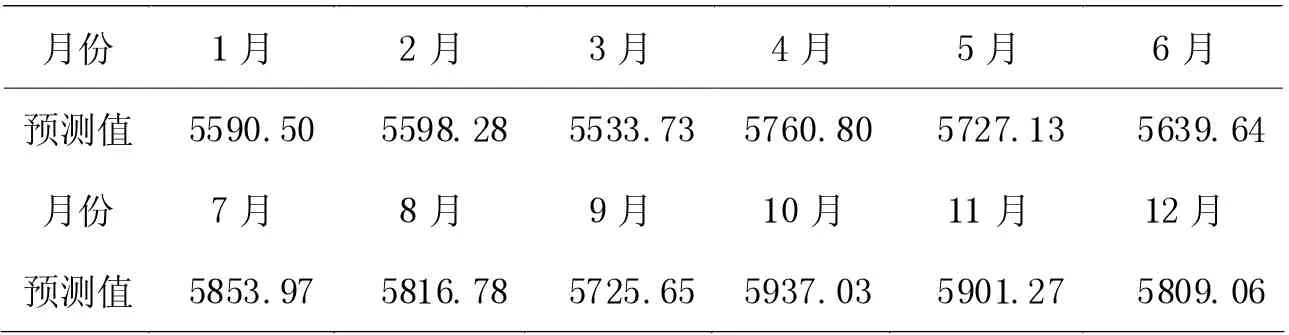
表4 2020 年旅客运输量预测
3 结论
本文选取了2007 年1 月至2019 年7 月连续139 个月的民航旅客运输量数据进行预测,建立了基于ARIMA 模型的旅客运输量预测模型,并使用2019 年8-12 月的真实数据进行验证,预测结果准确,说明了使用该模型进行建模预报是可靠的。但是,该模型未考虑突发事件对民航行业的扰动,在公共卫生事件、自然灾害、金融危机等情况下,该模型存在一定的局限性。在不考虑疫情的影响下,该模型能在民航正常运行的情况下较为准确地预测出旅客运输量,可供航空公司、机场等民航运行部门在资源保障和运力部署等方面提供决策支持。
