浮子获能评价指标研究与参数优化

王凯峰，张保成，苗 雨，邓子伟

(中国海洋大学 工程学院 机电工程系，山东 青岛 266100)

0 引 言

浮子是波浪能发电装置的重要组成部分。为优化浮子的结构参数，需要建立以浮子获能性能评价指标为基础的目标函数。传统上，一般以最大俘获功率、共振频率和俘获带宽作为评价指标。但是，这3个评价指标往往无法同时达到最优，需进一步确定最佳浮子参数组合。唐泽成[1]、SHAMI等[2]、SHADMAN等[3]在优化波浪能发电装置时采用最大俘获功率、共振频率和俘获带宽等3个评价指标计算不同尺寸参数的浮子对其的响应，再通过优化响应器(如minitab、taguchi)确定最佳参数组合。为解决各评价指标难以权衡的问题，可采用单一评价指标。史宏达等[4]、程正顺[5]、张亮等[6]、肖晓龙等[7]、RODRGUEZ等[8]用俘获宽度比(波浪能发电装置平均俘获功率与装置结构宽度范围内波浪入射功率的比值)来衡量波浪能装置俘获波浪能能力的强弱。何光宇[9]用响应幅值算子(Response Amplitude Operator,RAO)作评价指标来衡量浮子对波浪能的采集能力。PISCOPO等[10]以年效率作为波浪能发电装置获能性能的评价指标。SJÖKVIST等[11]用垂直方向浮子与波浪速度比来衡量浮子的获能性能。GOGGINS等[12]以有义速度为评价指标来优化浮子结构参数。SON等[13]使用浮子RAO与俘获宽度比作为评价浮子性能的指标。

可见，前人大多采用多目标优化方法或寻求有效的单一评价指标来开展该问题研究。然而，采用多目标优化的方式难以使多个评价指标同时达到最优，且所使用的评价指标中不包含海况信息，无法反映不同海况浮子的适用性。

本文基于前人的研究，利用浮子频域运动方程，推导一种能综合考虑海况与浮子俘获功率的浮子获能评价指标，以全面评价海况和浮子的结构参数对浮子获能的影响，为浮子的结构选型及参数优化提供目标函数。

1 浮子运动方程

浮子运动状态有垂荡、纵荡和纵摇等3种，垂荡运动[14]是浮子获能的主要方式，其他运动对获能贡献较小。为简化优化过程，只考虑浮子的垂荡运动。浮子与功率输出(Power Take Off，PTO)系统连接，PTO系统由弹性元件和阻尼元件组成。采用圆柱形浮子可忽略由波浪方向不同造成的差异。依据刚体动力学理论建立垂荡浮子运动的物理模型，如图1所示。

图1 单个装置结构示例

由于浮子垂荡运动范围远小于波长，因此基于微幅波理论建立浮子运动方程[15]为

(1)

式中：Ms为结构质量矩阵；Mh为波浪作用下的附加质量矩阵；X为RAO；C为系统总的阻尼矩阵；Ks为总的系统刚度矩阵；F为浮子受到的外部波浪力。

假定波浪能俘获装置的PTO阻尼为线性阻尼，且主要考虑浮子的垂荡运动获能，则垂向运动方程变为

(2)

式中：Ms为浮子质量；Mh为波浪附加质量；Z为垂荡运动幅值；RPTO为PTO系统阻尼系数；N为垂荡辐射阻尼系数；K为静水恢复力系数；Fe为物体所受垂荡方向上的波浪激励力。

因而浮子的垂荡频响为

(3)

式中：A为入射波波幅；ω为入射波频率。

浮子垂荡速度计算式为

(4)

2 能量俘获性能评价指标

2.1 评价指标推导

浮子吸收功率谱反映浮子在单位波幅(a(ω)=1)入射波激励下的动态响应特性。在随机波条件下，浮子系统的吸收功率PR为

(5)

俘获功率谱是指在单位波幅(a(ω)=1)入射波激励下的浮子获能功率，波幅a(ω)计算式为

(6)

把单位波幅条件a(ω)=1代入式(5)可求得在特定频率ωj下装置浮子俘获功率谱为

(7)

式(7)为能量俘获谱函数表达式，可建立浮子俘获功率谱以分析频谱参数(共振频率、共振带宽和最大俘获功率)。俘获功率谱为浮子自身属性，不包含海洋的波浪特征。

Ss(ω)为波浪动态速度响应谱，根据其定义，表达式为

Ss(ω)=(|H(iω)|ω)2S(ω)

(8)

式(8)包含波浪谱密度函数S(ω)。Ss(ω)可连接波浪参数与浮子获能性能。根据有义波高的物理意义，定义有义速度VS为

(9)

把式(8)代入式(9)，并将其离散化可得：

(10)

式(10)包含浮子的动态响应性能|H(iω)|ω和波谱信息S(ω)Δω，可更全面地分析俘获功率谱。但是，有义速度定义中不包括PTO阻尼系数，因此定义浮子获能评价指标f为

(11)

式中：D为水线处浮子结构的直径参数。

评价指标f的定义包含PTO阻尼系数和有义速度，分母中的浮子直径可用于比较不同尺寸浮子的获能特性。

为了更好地理解该获能指标的意义，把式(7)和式(10)代入式(11)可得：

(12)

由式(12)可知，该获能评价指标表征俘获功率谱和波谱在每个频率下乘积的总和，可较为全面地反映2个谱函数的匹配程度，更利于考察浮子获能能力。

2.2 评价指标与俘获宽度比的关系

俘获宽度比CW是评价波浪能发电装置获能效率的重要标准，其含义为

(13)

式中：Qw为装置结构宽度范围内入射波浪能量。根据式(11)、式(7)和式(13)，浮子获能评价指标、浮子俘获功率、俘获宽度比之间存在如下关系：

(14)

由式(14)可知，评价指标f与俘获宽度成正比，可将波能俘获效率转化为波谱与俘获功率谱的匹配问题，能更好地反映浮子获能能力，且采用单一的评价指标可以解决共振频率、共振带宽和最大俘获功率等3个优化目标难以权衡的困难。

3 新指标实例分析

以新型浮子获能评价指标为目标函数，采用AQWA-ISIGHT联合优化的方式对浮子的直径和吃水量进行优化。优化流程如图2所示。以批处理程序作为接口，实现ISIGHT对水动力分析软件AQWA的调用，在MATLAB中读取AQWA数据，实现对响应结果的计算[17]。

图2 浮子参数优化流程图

3.1 海况信息

选定青岛胶南市的斋堂岛东南海域为实际海况。杨忠良等[18]以该海域2013—2014年的实测波浪资料为基础，以JONSWAP谱为基础进行拟合，得到该海域波浪谱的表达式为

(15)

式中：α为无因次风区，其取值为0.006 2；ωp为谱峰频率；σ为峰形参量，当ω≤ω0时σ=0.07，当ω>ω0时σ=0.09。斋堂岛东南海域最大波高为5.3 m，最大周期为8.3 s，年平均有效波高为0.6 m，平均周期为3.3 s。

3.2 试验设计

试验设计是一种借鉴试验研究的思想进行数值求解的优化设计方法，可解决混合离散变量优化设计的问题。该方法利用正交试验安排搜索点，通过正交回归设计直接得到优化设计的搜索方向，所得方向与目标函数负梯度方向吻合，无须对目标函数求导，能大幅提高搜索效率，节省计算时间。以水动力学性能较好的圆柱形浮子为例，采用试验设计[19-20]的方法生成9组浮子尺寸。浮子尺寸范围如表1所示。

表1 浮子尺寸范围 m

利用试验设计思想，构造9组浮子结构尺寸的设计结果作为初始样本点，如表2所示，利用这9个样本点生成响应面模型(自变量的设计域)，之后在响应面模型上寻优。在ISIGHT的MATLAB组件中对这9组尺寸的浮子进行浮子响应计算。根据阻尼系数匹配理论选择各个外形尺度下的最优PTO阻尼系数，即当PTO系统与浮子处于共振频率时的辐射阻尼系数。

表2 响应面模型样本点

3.3 近似模型

响应面法(Response Surface Methodology,RSM)可利用多项式函数拟合设计空间。基于试验设计组的计算结果，采用RSM建立浮子的近似模型，流程如图3所示。对浮子响应的计算结果进行分析，得出响应面等量线图，如图4～图7所示。

图3 近似模型构建流程

图4 最大功率响应面等量线图

图5 共振带宽响应面等量线图

图6 固有周期响应面等量线图

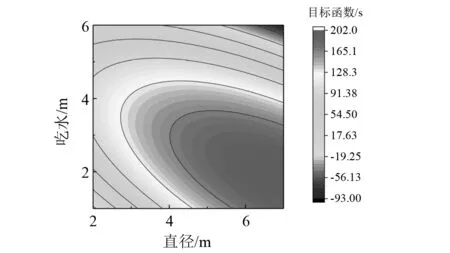
图7 目标函数响应面等量线图

3.4 参数优化

由响应面结果可知，浮子最大俘获功率与共振带宽无法同时达到最大，因此以所求得的评价指标f为目标函数求浮子参数的最优值。

NLPQL算法将目标函数以二阶泰勒级数展开，并把约束条件线性化，通过解二次规划得到下一个设计点，然后根据2个可供选择的优化函数执行一次线性搜索，其中Hessian矩阵由BFGS公式更新。将目标函数的响应面模型在ISIGHT中利用NLPQL算法进行优化，算法公式为

(16)

式中：DU和DL分别为直径D的上下限；LU和LL分别为吃水L的上下限。上述变量的值与表(2)中的值相同。最后，通过Optimization组件的计算，确定浮子在所设置范围内的最优参数为直径7.0 m、吃水1.8 m。

4 结 论

提出的浮子俘获性能评价指标以有义速度为基础，用每个频率下俘获功率谱和波谱乘积的总和来表征浮子获能能力，为浮子参数优化设计提供更能反映特定海域波浪条件下浮子获能综合性能的目标函数。进一步以斋堂岛东南海域海况为例，以该评价指标为目标函数，基于AQWA-ISIGHT联合仿真，对浮子的直径与吃水进行优化设计。由结果可知，以该评价指标作为目标函数进行浮子参数优化设计可更好地反映浮子对工作海域波况的适应性，验证了所提新型评价指标在理论上的合理性。