漂浮体系悬索桥拟静态纵向运动特性及其控制
2022-03-08梁龙腾封周权陈政清牛华伟华旭刚
梁龙腾,封周权,陈政清,牛华伟,华旭刚
(1.湖南大学风工程与桥梁工程湖南省重点实验室,湖南 长沙 410082;2.湖南大学汽车车身先进设计制造国家重点实验室,湖南 长沙 410082;3.广东省交通规划设计研究院集团股份有限公司,广东广州 510507;4.湖南大学重庆研究院 重庆 401133)
引言
随着我国交通建设事业的快速发展,一大批大跨度悬索桥相继建成。大跨度悬索桥多以漂浮体系或半漂浮体系为主,其优点是结构柔度大有利于抗震,缺点是纵向刚度小使得加劲梁容易在外部荷载作用下产生纵向运动[1-2]。因此学者们发现了大跨度悬索桥加劲梁纵向运动累积行程过大的现象[3-4],如矮寨特大悬索桥的加劲梁纵向运动单月累积行程超过4 km。加劲梁频繁的纵向往复运动会引起连接构件的性能退化和疲劳损坏[5-8],如润扬长江大桥通车5 年伸缩缝即部分部件疲劳损坏,江阴长江大桥的塔梁纵向流体粘滞阻尼器也因为漏油而性能退化[9]。这不仅提升了悬索桥的日常维护难度,也增加了地震防控的风险因素。明确漂浮体系悬索桥加劲梁纵向运动累积行程过大的成因,并找到有效的控制手段,对悬索桥健康安全运行十分必要。
国内外学者深入地研究了营运状况下悬索桥加劲梁纵向运动的成因问题。Ni 等[10]基于健康监测系统数据研究了汀九桥温度与主梁纵向位移之间的关系,研究发现加劲梁纵向运动位移与有效温度之间存在很强的比例相关性。邓杨等[11]研究了润扬长江大桥160 日梁端位移响应与钢箱梁温度实测数据的相关性,结果表明单日的梁端位移变化曲线变化趋势类似正弦曲线,而车辆荷载和风荷载引起的梁端位移运动表现为在位移变化趋势线上下浮动的现象。李光玲等[12]建立风-随机车流-钢桁悬索桥分析系统,研究了某钢桁悬索桥加劲梁伸缩缝在随机车流作用下的纵向位移时程响应,结果表明在随机车流作用下,加劲梁端伸缩缝处会产生不间断的往复运动,且其累积行程与交通流量存在线性关系。Guo 等[13]建立五峰山长江大桥有限元模型,研究发现漂浮体系悬索桥加劲梁在竖向活载作用下会产生纵向位移,且竖向活载位于加劲梁1/4跨时位移最大。万田保等[14]研究发现悬索桥加劲梁受到竖向非对称荷载会产生的纵向位移,且竖向荷载作用在加劲梁不同位置时梁端纵向位移相差悬殊,并指出主缆纵向刚度是大跨度悬索桥纵向刚度的重要来源,竖向荷载作用下引起的加劲梁纵向位移是悬索结构受力特征的体现。综上可知,目前针对漂浮体系悬索桥纵向运动的研究,主要是计算不同荷载下的纵向运动响应的正向问题,而基于实测位移时程研究各类荷载所产生的运动占比与贡献的逆向研究并不多见。且目前仅有少量文献关注纵向累积行程过大的问题。
学者们也对加劲梁纵向振动控制问题进行了相关研究。丁幼亮等[15]研究了风致抖振引起的主梁振动控制问题,采用液体粘滞阻尼器进行振动控制,减振效率可以达到50%左右。张宇峰等[16]在加劲梁梁端安装阻尼器降低车致振动振幅,对改善伸缩缝的工作状态起到了积极作用。张鑫敏等[17]提出在塔梁连接处设置静力限位-动力阻尼装置对虎门二桥坭洲水道桥的纵向运动进行控制,梁端位移幅值减小23.6%。可以发现,现阶段加劲梁纵向振动控制研究主要以振动幅值作为评估指标,而以累积行程作为评估指标的文献较为少见,实际上累积行程才是伸缩缝等梁端连接装置疲劳破坏的根源。
文中以未安装阻尼器状况下的江阴长江大桥24 h 加劲梁纵向运动时程为基础,采用EMD 和AMD 等信号处理方法将时程曲线分解为3 种不同频谱特性的位移成分,并基于雨流计数法研究各位移成分在循环次数和累积行程中所占比例;研究了在累积行程占比高的拟静态纵向运动成分的产生机理,并以产生机理为理论基础,反演得到了等效竖向荷载时程;研究了拟静态纵向运动的控制措施问题,提出了一种有效的控制方法。文中有助于进一步了解漂浮体系悬索桥纵向运动特性,也为漂浮体系悬索桥拟静态纵向运动分析和累积行程控制提供理论基础。
1 漂浮体系悬索桥纵向运动特性分析
1.1 研究背景
文中以江阴长江大桥作为研究对象。江阴长江大桥主跨跨径1 385 m,矢跨比1/10.5,主缆中心距32.5 m,吊索间距16 m。加劲梁形式为扁平闭口流线型钢箱梁,梁高3.0 m,梁宽36.9 m,是一座典型的漂浮体系悬索桥。健康监测系统在加劲梁南北两端的上下游两侧分别布置1 台,共4 台位移传感器采集加劲梁的纵向运动数据。上下游两台位移传感器的间距为12 m,采样频率1 Hz,数据采集时间为24 h,如图1 所示。该24 h位移时程数据为2006年3月30日未安装塔梁间纵向阻尼器时所采集。
从图1 可知,加劲梁同一端的两台位移传感器采集的位移时程曲线整体运动趋势基本一致。由于昼夜温差导致的加劲梁纵向变形趋势明显,当白天温度升高时加劲梁变长,南岸端往正向移动,北岸端往负向移动;而在晚上降温时加劲梁缩短,南岸端往负向移动,北岸端往正向移动,两端的整体移动趋势刚好相反。
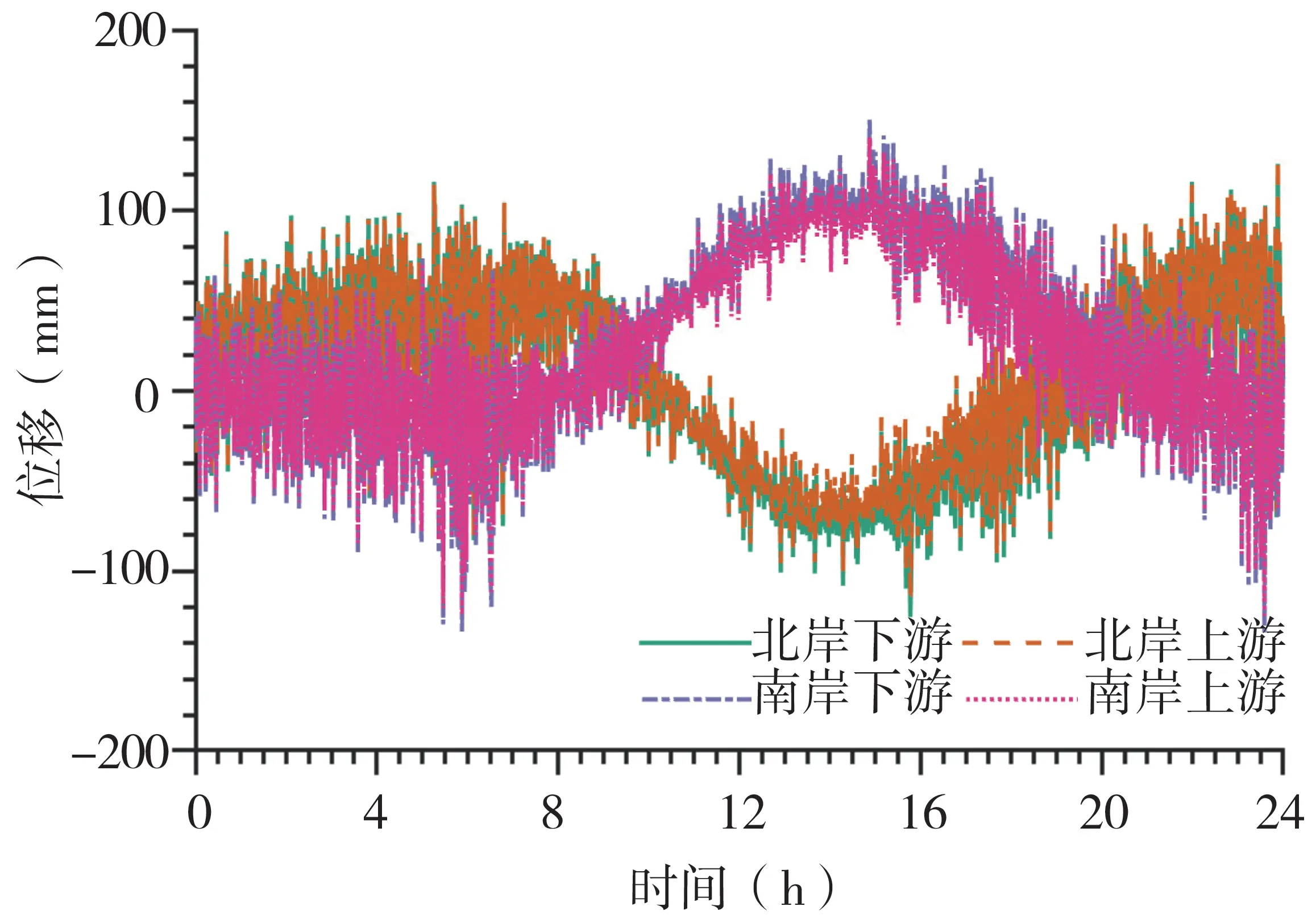
图1 加劲梁纵向运动24 h位移时程曲线Fig.1 24 h measured longitudinal displacement of stiffening girder
1.2 频谱特性
计算实测24 h加劲梁纵向运动位移时程曲线的功率谱密度(PSD)特性如图2所示。将图2中PSD曲线的纵向振动卓越频率与Brownjohn[18]和Zhou[19]实测的江阴长江大桥的卓越频率进行对比,验证文中采用的实测位移时程曲线的准确性。这两篇文献中进行了全桥振动响应的实测和模态识别,包含竖弯模态和侧弯模态。这里仅将与图2前三阶振动卓越频率对应的模态提取出来进行对比,如表1所示。结果表明,文中纵向位移时程曲线的卓越频率与文献中的数据吻合良好,从侧面证明文中的纵向运动时程曲线的真实性和准确性。

图2 加劲梁纵向运动24 h位移时程频谱特性Fig.2 Spectrum characteristics of 24 h longitudinal displacement of stiffening girder
结合图2 与表1 可以发现,加劲梁的纵向运动从频谱特性的角度可以分成3 个部分:第1 部分是昼夜温差引起的加劲梁伸缩变形(以24 h为一循环,频率为1/86 400 Hz=1.157×10-5Hz);第2部分是拟静态因素引起的频率远小于一阶纵向振动频率的纵向往复运动(卓越频率为0.005 9 Hz);第3部分为高于和等于一阶纵向模态频率的纵向振动响应(频率≥0.104 Hz),对应由风荷载和车辆荷载等动力因素激励引起的加劲梁纵向共振响应。为了控制加劲梁纵向运动,避免连接构件疲劳损坏,可以将位移时程按照频谱特性进行分解,针对性的研究其控制方法。

表1 实测卓越频率对比Table 1 Comparison of measured spectral characteristics
1.3 信号分解
由昼夜温度变化引起的加劲梁纵向运动,实际是材料热胀冷缩引起的纵向位移,不作为纵向运动控制目标,所以首先需要将其从运动时程曲线中剥离出来。以北岸下游的位移时程曲线为例,采用EMD 方法进行分解,将提取出来的残差与实测位移时程曲线对比,如图3(a)所示。EMD方法是一种时域数据处理手段,EMD 分解信号得到IMF这个过程完全是依赖于信号本身的,是一个自适应的过程,同时是后验的,并且能够避免基于傅里叶变换分析导致的能量扩散、泄露等问题[20]。从图3(a)可以发现,EMD 残差为纵向位移一天内的总体趋势,与温度变化产生的梁端位移变化特性相符合。而所有本征模函数(IMF)之和曲线,如图3(b),是移除了温度变化位移的时程曲线,其频谱特性曲线与实测时程曲线的频谱特性进行对比,如图3(c)所示。由图可知,温度引起的梁端位移变化可以视为周期是24 h的纵向运动,其频率为1/86 400 Hz,很明显可以看到该频率成分已经被剔除。

图3 加劲梁位移时程曲线的EMD分解Fig.3 Decomposition of displacement time history of stiffening girder with EMD method
由1.2节内容可知,IMF之和曲线中包含了纵向振动响应和拟静态纵向运动,为了分解两种成分,这里引入AMD方法进行截断处理,得到不同频率特性的数据曲线。AMD方法是基于HHT的时域信号处理方法,避免了频域加窗导致的信号失真的影响[21-22]。其基本原理为当信号x(t) =s1+s2,如果低频成分s1与高频成分s2的频谱不重叠,则存在截断频率ωb使得,

式中:ωb数值大于s1的最高频率且小于s2的最低频率;H为希尔伯特变换。利用AMD 方法可以快速地将信号分解为低频和高频两部分。
选择0.02 Hz作为截断频率,将IMF之和的时程曲线分成2个部分,如图4所示。观察图中的频谱特性可以发现,IMF之和曲线以截断频率为界线分成了2条频谱特性完全不同的位移时程曲线,分别对应加劲梁的拟静态纵向运动和纵向振动响应,如图5。

图4 加劲梁位移时程AMD分解后的频谱特性Fig.4 Spectral characteristics of displacement time history of stiffening girder after AMD
对图5 中由AMD 方法分解得到的加劲梁位移时程曲线的运动幅值进行统计。拟静态纵向运动位移时程中位移最大值为92.3 mm,最小值为-123.5 mm,行程范围(最大值-最小值)为215.8 mm,位移标准差为23.9 mm;纵向振动响应位移时程的位移最大值为16 mm,最小值为-14.3 mm,行程范围为30.3 mm,位移标准差为2.5 mm。可以发现,不同频谱特性的加劲梁纵向运动成分,其往复运动的位移幅值、标准差等特性区别很大,拟静态纵向运动的位移幅值和标准差均远大于纵向振动响应。为了针对性的找到对不同特性的纵向运动的控制措施,需要进一步的分析其特性和影响。

图5 AMD分解后的加劲梁位移时程Fig.5 Displacement time history of stiffening girder after AMD
1.4 特性分析
利用雨流计数法对图3(a)中实测位移时程曲线的峰峰值-循环次数特性进行统计。雨流计数法最早提出是在疲劳损伤领域,这个方法被用来统计随机载荷的分布,通过建立随机载荷的往复循环分布和其引起的结构应力-应变循环之间的关系,从而根据材料损伤理论分析应力-应变滞回曲线与结构损伤与破坏的关系。
统计位移时程曲线的峰峰值-循环次数特性的分布关系,如图6所示,这里峰峰值的定义为单个运动循环的波峰与波谷之差。图中将峰峰值以2 mm 作为单位区间进行统计,柱状高度对应各峰峰值区间的循环次数。由图可知,峰峰值在0~2 mm 区间的循环次数有8 034 次,数量最多;而随着峰峰值越大对应的运动循环次数越少。结合上一节中两种不同加劲梁纵向运动成分的特性,可以发现,拟静态纵向运动的位移行程大,但是循环次数少,而纵向振动响应的位移行程小,但是循环次数多。
为了定量地给出两种纵向运动成分所占比例,可将纵向振动响应位移时程曲线的行程范围值30.3 mm作为分界线,行程幅值小于30.3 mm 的计入纵向振动响应,行程幅值大于30.3 mm 而小于215.8 mm 的计入拟静态纵向运动。唯一幅值大于215.8 mm 的循环是由于温度变化引起的位移循环。统计出循环次数和循环累积行程的占比,如图6所示。可以发现,虽然纵向振动响应在循环次数中占据了95.91%,但是大幅值的拟静态纵向运动在累积行程中占据了76.34%。

图6 加劲梁实测位移时程的统计特性Fig.6 Statistical characteristics of measured longitudinal displacement of stiffening girder
由于随机风荷载和车辆荷载引起的纵向振动响应可以通过安装速度型阻尼器进行有效的控制,如梁龙腾等[23]提出用电涡流阻尼器进行悬索桥加劲梁纵向共振响应控制,收到了很好的效果。所以有效地控制住拟静态纵向运动是避免加劲梁连接件的疲劳损坏和性能退化的关键。
2 拟静态纵向运动成因分析
找到拟静态纵向运动的成因不仅有助于理解悬索桥纵向运动,也能够对后续的振动控制研究提供参考。本节通过建立江阴长江大桥的有限元模型,对拟静态纵向运动的成因进行探索研究,见图7所示。采用通用有限元软件ANSYS建立模型,主塔和加劲梁采用Beam4 单元进行模拟,主缆和吊杆则采用Link10 单元进行模拟,模型共有节点945个,单元948个。

图7 江阴长江大桥有限元模型Fig.7 Finite element model of Jiangyin Bridge
2.1 特性分析
车辆行驶在悬索桥加劲梁上,加劲梁受到车辆竖向荷载的作用。为了研究竖向集中力对加劲梁梁端纵向运动的影响规律,在加劲梁上1/4 处施加一个集中力如图8 所示。通过调整变形比例因子,可以发现在竖向集中力的作用下,加劲梁不仅产生了竖向的位移,也出现了纵向的位移,纵向位移的出现是主缆、吊杆和加劲梁共同作用的结果。这种存在于桥上的不对称竖向荷载就会引起加劲梁产生纵向运动,这与加劲梁的纵向共振位移响应的发生机制明显不同。

图8 拟静态纵向运动成因Fig.8 Cause of quasi-static longitudinal motion
进一步的,当一个2 000 kN 的竖向集中力荷载由北往南依次加载在加劲梁的节点上,此时加劲梁两端、跨中和南北1/4 跨5 个位置处的纵向位移,即5 个节点的影响线绘制如图9,图中负向为往北岸移动,正向为往南岸移动。由图可知,5个点的运动趋势基本一致,加劲梁在受到竖向的2 000 kN集中力的作用时出现整体的纵向移动;且当竖向集中力位于在1/4跨位置时,加劲梁的纵向位移最大。

图9 加劲梁节点的纵向位移影响线Fig.9 Longitudinal displacement influence line of stiffening girder nodes
悬索桥加劲梁上任意分布的竖向车辆荷载可以分解为正对称分布和反对称分布2 个部分,正对称分布荷载由于两者相互抵消不会产生加劲梁的纵向位移,文中所述的拟静态纵向运动则是由竖向车辆荷载的反对称分布部分造成的。为了简便起见,按照加劲梁梁端位移相等原则,将不对称车辆荷载因素简化为一个加在悬索桥加劲梁1/4 跨处的等效竖向集中力。因为文中关注的重点为加劲梁的梁端纵向位移,其他构件的变形并不在文中的考察范围,用一个竖向集中力进行等效,产生与实测数据相同的梁端拟静态位移,可以简化分析流程,且不影响分析结果。
同时,当一个集中荷载从桥的一端向另一端移动时,加劲梁完成一个纵向往复周期,周期与集中力过桥时间相等,当集中力以时速60 km 通过江阴长江大桥1 385 m 长的主跨时,加劲梁纵向运动频率为0.012 Hz,与采集到的拟静态纵向运动的卓越频率0.005 9 Hz 较为接近。实际上的不对称荷载分布是非常复杂的,可能由随机分布的多辆重车造成。1.3 节采用AMD 方法进行数据分解时,选择了0.02 Hz 作为截断频率,包含了时速100 km以下的不平衡竖向力运动,与实际情况相符。
2.2 等效集中力反演
虽然确认了拟静态纵向运动的成因,并采用AMD 方法分解得到了位移时程曲线,但是无法借鉴加劲梁的纵向振动响应时程,基于其卓越频率建立单自由度模型体系计算荷载时程曲线,从而进行振动控制评估的方法[18]。基于拟静态纵向运动的形成机理,反演出等效竖向集中力荷载时程曲线,可以避免求解随机车辆荷载过桥时程分析的难题,显著降低拟静态纵向运动控制研究的工作量。
以加劲梁南岸1/4 跨处作为加载点,施加大小为-3 000 kN 至3 000 kN 的竖向集中力,计算出竖向集中力与纵向位移的对应关系,如图10。由图10(a)可知,在竖向集中力作用下,加劲梁纵向运动趋势一致,数值基本相等,说明采用单点加载的方法能够很好的实现加劲梁的拟静态纵向运动,而且位移范围也涵盖了拟静态纵向运动-123.5 ~92.3 mm的行程范围。仍然采用北岸端点的数据来进行多项式拟合,如图10(b)。拟合计算得到多项式如式(2),

图10 加劲梁拟静态纵向运动的集中力-位移关系拟合Fig.10 Curve fitting of the relationship between vertical concentrated force and quasi-static longitudinal displacement

多项式拟合的R2系数为1,说明该多项式具有很高的拟合精度。
结合图5(a)中的拟静态纵向运动位移时程曲线和式(2)的集中力-位移关系式,就可以反演出加载在南1/4 跨处的等效竖向集中力荷载时程曲线,如图11 所示。将等效竖向集中力输入到悬索桥有限元模型进行时程分析,对比计算得到的有限元模型加劲梁北端节点的纵向位移时程曲线与实测得到的拟静态纵向运动时程曲线(第3.5 至5.5 h),如图11(b)。由图可知,采用等效竖向集中力加载的方法可以有效还原实测分解得到的拟静态纵向运动,采用该方法可以很方便地评估各类控制装置对拟静态纵向运动的控制效果。

图11 等效集中力的反演与验证Fig.11 Identification and verification of equivalent force
3 拟静态纵向往复运动控制分析
漂浮体系悬索桥加劲梁纵向运动中,温度变化产生的变形位移需要进行释放,避免出现巨大的温度内应力;纵向振动响应成分通过安装电涡流阻尼器提高阻尼系数可以进行有效的限制[18];文中对在累积位移中占比最大的拟静态纵向运动的控制措施进行分析。通过在加劲梁与主塔横梁的节点之间添加Combin37单元模拟速度型阻尼和极限摩擦力等控制措施,为了便于理解,这里定义控制率ρ,如式(3)来评估控制效果。

式中:DSUM为安装控制装置的累积行程;D0SUM为未安装控制措施的累积行程。控制率越高,说明控制效果越好。
首先考虑增加阻尼系数对拟静态纵向运动的控制效果,阻尼系数工况如表2,计算出各个工况下的加劲梁位移时程曲线,并计算出其累积行程,如图12所示。可以发现,增大阻尼系数对加劲梁拟静态纵向运动的控制效果并不理想,累积行程也没有显著的降低,阻尼系数提升到80 000 kN·s/m,累积行程的控制率也只仅为7.46%。这是由于阻尼系数和速度呈正比,当加劲梁运动保持低速度运动时,阻尼力也相对较小,无法有效的抑制拟静态纵向运动。如果阻尼系数过大,阻尼器及其连接构件很容易因为其循环往复运动而出现疲劳损坏问题,同时阻尼器及其连接构件的制造成本也将大增。

图12 阻尼系数对拟静态纵向运动的影响Fig.12 Influence of damping coefficient on quasi-static longitudinal motion

表2 阻尼控制工况表Table 2 Damping coefficient for different cases
这种现象在江阴大桥实际阻尼器的控制效果也得到了验证。通过对比江阴长江大桥安装阻尼器前后的位移时程曲线的频谱特性,可以评估速度型阻尼对加劲梁纵向运动的控制效果。2007 年2 月江阴长江大桥安装了4 台流体粘滞阻尼器(阻尼系数1 522 kN/(m/s)0.3,速度指数0.3,最大阻尼力1 000 kN)来控制大桥的纵向运动。将 北 岸 上 游 侧2007 年3 月30 日 和2006 年3 月30日的位移时程功率谱密度曲线绘制如图13 所示。由图可知,增加了粘滞阻尼器后,纵向振动响应部分得到了有效的控制,其卓越频率处的幅值明显下降;而拟静态纵向运动部分的卓越频率并没有明显的变化。这从实测的角度表明单独采用速度型阻尼器无法有效地控制悬索桥加劲梁的拟静态纵向运动。

图13 阻尼器安装前后位移响应功率谱对比Fig.13 Comparison of displacement PSD before and after damper installation
为了提高低速状况下的阻尼力,可以采用具有库伦阻尼形式的摩擦阻尼器来控制拟静态纵向运动,这里设计的极限滑动力Fs工况如表3,计算对应的位移响应时程,统计其累积位移如图14 所示。由图可知,摩擦阻尼能够有效地抑制加劲梁的拟静态纵向运动,随着极限滑动力的增大,拟静态纵向运动的累积行程逐渐减小;当极限滑动力为400 kN 时,对拟静态纵向运动的控制率达到67.08%,远优于提升阻尼系数的控制方法。同时发现,累积行程虽然随着极限滑动力的增大而逐渐减小,但是控制率的增加速度逐渐放缓。

图14 极限滑动力对拟静态纵向运动的影响Fig.14 Influence of limiting sliding force on quasi-static longitudinal motion

表3 极限滑动力工况表Table 3 Sliding force for different cases
进一步的,可将速度相关型阻尼和摩擦阻尼并联组合应用在悬索桥加劲梁的纵向减振控制中,这样可以同时具备高速时的速度相关阻尼特性和低速时的库伦阻尼特性。采用并联方案控制拟静态纵向往复运动,设计的工况如表4,对应的控制率绘制如图15所示。由图可知,在不同阻尼系数的情况下,增加极限滑动力都可以有效的抑制拟静态纵向运动的累积行程;同时,当极限滑动力确定,增大阻尼系数也在一定程度上能够抑制累积行程的增长。另一方面,速度相关型阻尼可以非常有效的降低纵向振动响应成分,这个结论已在另一篇论文中进行了充分的验证[23]。由此可见,速度相关型阻尼和摩擦阻尼并联组合控制具有良好的控制效果,是加劲梁纵向运动综合控制的有效方向。

图15 组合控制对拟静态纵向运动累积行程的影响Fig.15 Influence of combinational control method on cumulative stroke of quasi-static longitudinal motion
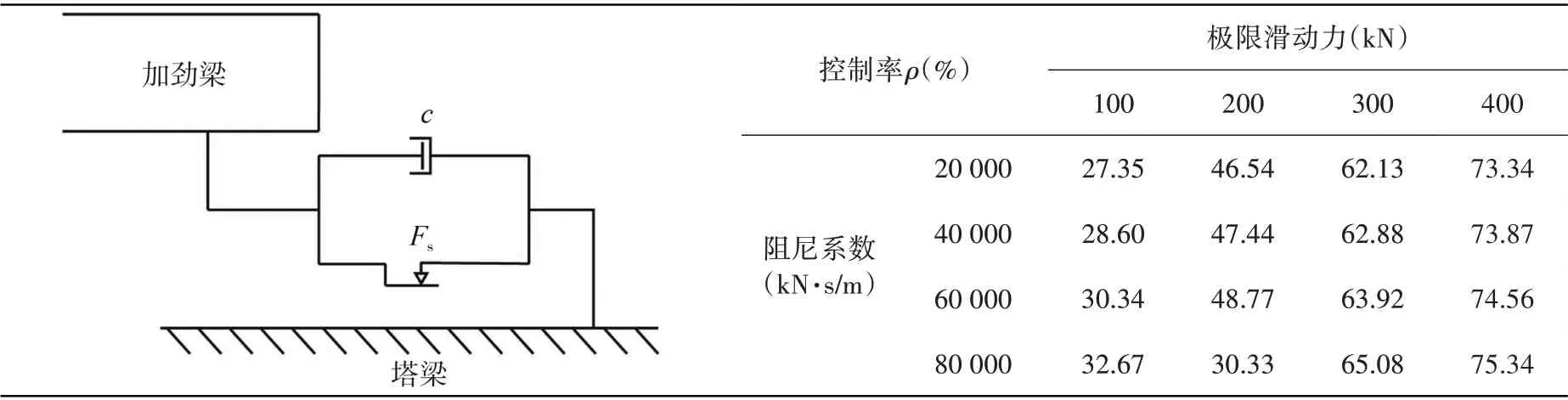
表4 组合控制工况表Table 4 Combination control method for different cases
对于采用刚度对拟静态纵向运动进行控制的位移型阻尼器,如软钢阻尼器等,由于无法释放因为温度变化加劲梁变形产生的温度内应力,所以采用该类型阻尼器进行纵向位移控制不是合理的选择。
结合上述分析,速度阻尼能够抑制高速度的振动,但是对低速的拟静态纵向往复运动的抑制效果较差;而摩擦阻尼器在低速时能够提供较大的阻尼力,从而非常适合用来抑制加劲梁拟静态纵向运动;二者并联组合方案是加劲梁纵向运动综合控制的有效方向。
4 结论
(1)对加劲梁纵向位移时程曲线的分析和分解表明,纵向位移可以分为温度变化引起纵向伸缩变形,拟静态纵向运动和低频振动共振3 个部分。拟静态纵向运动在累积行程中占比超过70%,进行纵向运动控制时不能忽略其影响。
(2)加劲梁的拟静态纵向运动是由于车辆荷载在悬索桥加劲梁上的不对称分布造成的。为了简便起见,按照加劲梁梁端位移相等原则,将车辆荷载简化为一个加在悬索桥加劲梁1/4跨处的等效竖向集中力进行处理。
(3)基于拟静态纵向运动的产生机理,反演得到等效竖向集中力,可以有效还原实测分解得到的拟静态纵向运动,且该等效集中力能够方便地评估各类控制装置对拟静态纵向运动的控制效果,并避免了采用随机车流模型模拟过桥的难题,简化了计算流程。
(4)采用速度型阻尼器与摩擦阻尼器组合的方式,可以有效的抑制加劲梁的拟静态纵向运动。
