基于随机森林的中小跨径公路梁桥双柱墩地震易损性模型
2022-03-08鲁冠亚王克海邱文华张秉哲
鲁冠亚,王克海,邱文华,张秉哲
(1.东南大学交通学院,江苏 南京 210096;2.交通运输部公路科学研究院,北京 100088)
引言
中小跨径梁桥是最常见的桥梁类型,是我国高速公路网络的重要组成部分。汶川地震震害显示中小跨径公路梁桥多采用双柱墩,桥墩易出现开裂、压溃和倾覆等破坏,导致交通系统的中断,对经济产生影响[1]。在对区域或线路中的每一座中小跨径梁桥进行建模和地震易损性评估是不可行的,因此,有必要参数化表征桥梁群组并建立数值分析模型进行易损性评估。近年来,报道的文献已经形成了不同区域的桥梁数据库,例如美国加州[2],欧洲土耳其[3]、希腊[4]、意大利[5]等,虽然这些研究成果建立了区域桥梁的桥墩和支座等构件的地震易损性曲线,但在建立过程中采用的主观分类和传统的分析方法存在诸多不足,例如:(1)采用方差或协方差分析不同桥梁类型的地震响应时,必须满足处理效应的独立性和方差齐次性假设[6];(2)采用概率地震需求模型时,地震需求的对数正态性假设和恒定离差假设是地震易损性分析的主要误差来源[7],并且在高强度地震动时,桥梁构件将经历非线性行为,导致其概率需求模型的回归效率降低。上述假定对桥梁地震易损性的准确性造成了一定的偏差,而没有假定则无法做任何经典统计推断;(3)传统方法以单参数(地震动强度(IM))为条件回归建立易损性,无法确定其他桥梁属性在地震易损性中的相对重要性。
随机森林(RF)是一种流行的机器学习技术,与其他机器学习技术相比,RF是依赖于一系列不等式规则的学习算法,不对映射函数进行任何强有力的假设,并且是非参数的[8]。近年来,在工程结构的地震响应分析和性能评估中已经有所应用。例如,Tesfamariam 等[9]研究了包括RF 在内的机器学习技术在过去地震对建筑物损伤状态分类中的应用。Jia 等[10]使用了汶川地震的桥梁数据,根据随机森林模型进行了结构、场地和支座类型等9 个特征的重要性排序,并判断了桥梁的地震损伤。Mangalathu 等[11]在为加州三跨和四跨桥梁建立了构件易损性曲线的过程中,采用随机森林建立了构件多维参数下的需求模型,但未考虑构件实际的能力模型,依然采用了传统的对数正态分布。吴晓阳[12]采用回归决策树方法建立了场地地震动预警参数指标,指出该快速评估方法的总体成功率达到90%以上。
文中提出了一种结合增量分析法和RF技术为特定线路中小跨径梁桥的双柱式桥墩建立地震易损性曲线的方法。基于上述文献,以下2 点值得关注:(1)已有研究采用RF 技术仅建立了构件的地震需求模型,未关注构件的抗震能力模型[11];(2)中国桥梁的结构体系、材料性质、构造设计与美国桥梁存在差异,直接引用推荐值是否会导致偏差[13]。文中以一条山区高速公路为研究对象,首先采用统计工具得到其桥墩的结构、几何和材料特性的概率分布,由拉丁超立方体抽样(LHS)为该线路中小跨径梁桥生成桥墩属性数据集,建立参数化的有限元模型。然后通过Pushover分析和基于非弹性需求谱的能力谱方法获取双柱墩的地震需求和抗震性能数据点,检验需求值和能力值的对数正态分布假设,进一步利用RF算法建立双柱墩的地震易损性模型,并与传统方法进行比较,说明RF建立易损性曲线的优点。
1 随机森林
随机森林是在决策树为基学习器构建套袋集成的基础上,进一步在决策树的训练过程中引入了随机属性选择[8]。在套袋中使用训练数据重复采样独立地构建每棵树,最终输出所有树结果的平均值进行预测,一般算法如下:
(1)随机且有放回地从训练集中的抽取nt个训练样本。
(2)随机选取包含k个属性子集,得到最佳分割,从每个样本生成决策树。
(3)通过nt个决策树的平均值预测新数据集的输出。
RF预测的输出可表示为:
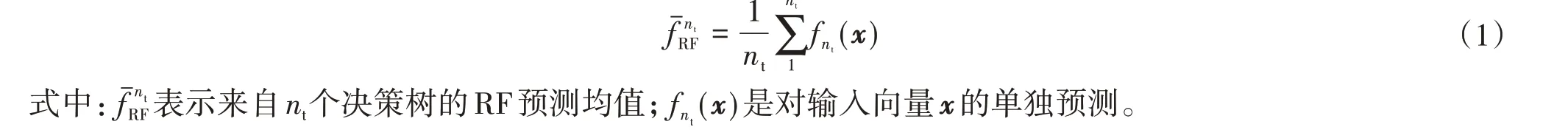
RF 依据计算袋外错误率(OOB)选择最优的特征子集,首先使用每次重复抽样得到样本的生长树,对每棵树的袋外样本进行预测,然后计算预测产生的OOB。
图1展示了采用2个变量x1和x2分配预测A,B,C,D或E的单颗树。树起初基于变量x1划分区域,若x1≥a1,则树的左支被激活,A,B或C的分配取决于x2的值a2和x1的值a4。若树的右支被激活,根据变量x2预测变量D或E。RF由随机选取特征创建了大量的决策树,由每个决策树的平均预测产生输出。

图1 单颗树二变量示意Fig.1 Illustration of a tree with two variables
在特征自变量的重要性判断中,RF 采用基尼指数(GI)的降低值作为分类问题中特征重要性排序的指标,式(2)计算数据集D的基尼指数,其意义为删除某个自变量后所有RF树中每个特征的节点分裂不纯度变化的平均值,该指标变化越大说明变量越重要。

式中:pv为数据集D中第v类样本所占的比例(v=1,2,…,V);Dv为属于第v类的样本子集;a和V表示离散特征a可能具有的V个取值。
2 双柱墩的属性统计和数值模拟
2.1 属性统计
文中采用新建汶川到马尔康高速公路中小跨径梁桥的589 个桥墩信息,该线路桥梁主要为桥面连续的预应力混凝土简支T梁桥和预应力混凝土连续箱梁桥,简支梁桥跨径一般为30 m或40 m,主梁宽度为12 m;连续梁桥主梁采用单箱多室,单跨跨径分布于20~40 m,主梁宽度分布于8.5~16.5 m。2种桥型的桥墩采用了不同的配置,前者为有盖梁的双柱墩,后者中墩采用无盖梁形式(排架墩),均为圆形截面。支座采用板式橡胶支座,基础均采用柱式桩基础,无承台。
简支梁桥在每片T梁下设置板式橡胶支座,连续梁桥在排架墩2个柱顶分别设置一个板式橡胶支座。由式(3)定义板式橡胶支座刚度几何系数,统计该值与跨径和主梁宽度的关系,简支梁30 m跨径时,为2.2~2.6;40 m跨径时,为2.6~3.2。连续梁的支座刚度几何系数与跨径和主梁宽度有一定的相关性,可按主梁宽度保守地取为每沿米主梁宽度的0.3~0.5倍。

式中:Ar为支座剪切面积;Σt为橡胶层的总厚度。
统计所调查线路中桥梁群组的双柱墩结构、几何和材料等属性,由于桥墩的设计指标会受其他因素的影响,需要对各指标的统计数据做相关性分析,计算各指标的Spearman 相关系数,该相关系数对变量的分布不作要求,可评估2个连续变量之间的单调关系,一般认为相关系数在0.5~0.8时,两变量显著相关[14]。统计桥墩的盖梁长度、柱间距与主梁宽度,结果表明,盖梁长度和主梁宽度具有较明显的相关性,通常二者相等;当主梁宽度为标准12 m 时,柱间距为7 m,遇到较陡横坡地形,柱间距采用4.75 m;当主梁宽度非12 m 时,柱间距为主梁宽度的0.4~0.55 倍。对跨径、柱高、横向柱高比、柱间距、柱径以及纵筋率和配箍率进行相关性分析,得出的相关系数矩阵,如图2所示,结果表明墩柱直径与跨径、柱高和柱间距存在较为明显的相关关系,不能作为独立变量,其他指标之间无明显相关性,可作为独立变量。

图2 桥墩各指标相关系数矩阵Fig.2 Correlation matrix of the pier indices
根据桩基设计参数(桩径与桩长)和土层信息,对统计的桥墩基础采用“m”法[15]计算其平动刚度和转动刚度,得到基础刚度的分布。
对于统计的离散型数据,生成相应属性的非参数概率质量函数;对具有连续型随机变量特性的桥梁属性,采用Kolmogorov-Smirnov(K-S)拟合优度检验经验分布是否符合某种理论分布,即通过比较理论分布和经验分布的累积密度函数之间的最大垂直距离Dn判断两分布是否一致,若Dn的p值大于显著性水平(工程中一般采用0.05),则认为两分布一致[14]。表1总结了可视为独立变量的桥墩属性的统计分布和K-S检验p值,材料等属性的统计分布直接应用规范或已有文献采纳的统计分布值。

表1 桥墩属性统计分布Table 1 Statistical distributions of the pier properties
由双柱墩的系梁设置发现,对于有盖梁桥墩,桥墩高度大于12 m 设置1 根系梁,大于20 m 设置2 根系梁。对于排架墩,第1根系梁顶部距离柱顶0.3~0.5 m,当墩高大于12 m时设置第2根系梁。以墩柱顶部(盖梁底部)到系梁顶部的距离与柱高的比值为指标表示系梁在墩柱的位置,该指标可满足正态分布,见表2。系梁采用矩形截面,高度一般小于柱径0.2 m,高宽比约为1.15。
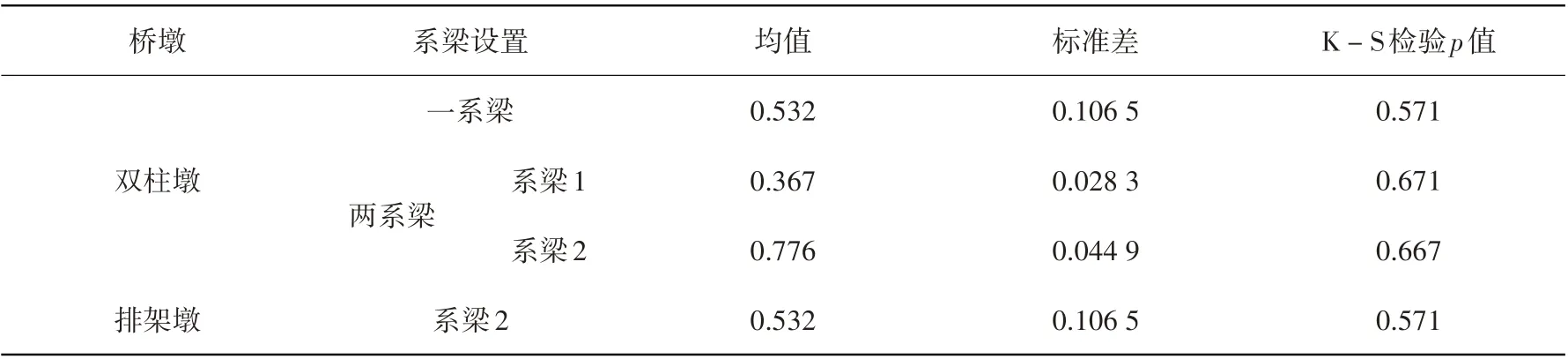
表2 系梁位置指标分布Table 2 Distributions of the tie beam location indices
2.2 建立总体和参数化有限元模型
根据统计的桥墩属性,采用LHS 模拟概率分布函数中的可能值生成桥墩总体。LHS 是一种分层随机过程,提供了一种从变量分布中抽样的有效方法[16]。在k个独立变量X1,X2,…,Xk中,LHS 对每个变量的累积分布分为N个等概率间隔,从每个间隔中随机选择一个值,每个变量获得的N个值再与其他变量随机配对,抽样生成样本。由LHS生成具有95%保证率的1 200个桥墩样本,基于有限元平台OpenSEES[17]建立参数化的双柱墩空间有限元模型。由弹性梁单元模拟盖梁和系梁,弹塑性纤维梁单元模拟墩柱。混凝土和钢筋纤维分别采用Mander 模型和双折线模型。由于仅研究双柱墩的易损性,所以,以集中质量点的形式考虑上部结构质量,各质量点之间以及质量点与支座顶部均采用刚臂连接,支座和桩基础采用线性弹簧模拟,有限元模型如图3所示。

图3 双柱墩数值模型Fig.3 Numerical models of double column piers
3 基于RF的双柱墩易损性模型
3.1 双柱墩的地震需求和能力分析
由于中小跨径梁桥主要以一阶振型控制为主,高阶振型对结构的影响可忽略不计,所以,在桥墩顶部位置施加固定荷载模式,采用位移控制的拟静力加载方法[18-19],即在桥墩顶部开始施加使墩顶产生逐级位移的单调递增侧向荷载模式,如图4所示。在整个Pushover的过程中,监测每级加载位移下混凝土和钢筋的应力应变、沿墩身各截面的曲率和桥墩顶部的位移,从材料和构件层面进行对应,使桥墩经历由弹性到屈服,进入塑性以及最终破坏的全过程,标记出控制桥墩各损伤极限状态的墩顶位移,表征双柱墩的地震需求和能力值。
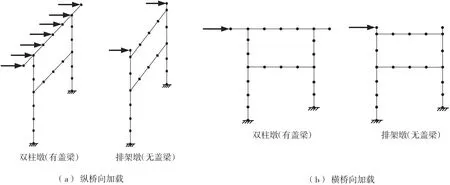
图4 Pushover加载模式Fig.4 Loading modes of Pushover
基于非弹性需求谱的能力谱方法[20]计算所需IM 下双柱墩的位移需求,以位移延性系数作为工程需求参数,需求谱阻尼比为5%。能力谱法的步骤如下:
(1)通过Pushover分析确定基底剪力Vb和顶部位移Dt曲线,按式(4)将Pushover曲线转化为能力谱。

式中:A和D分别为拟加速度谱和拟位移谱;M1*为基本振型的有效质量(模态质量);Γ1为基本振型参与系数;φ1为基本振型在顶部的振幅。
(2)将上步所得的力-位移关系转化为理想的弹塑性形式,理想化双线性系统的弹性周期T*为:

式中,Fy*和Dy*分别为屈服力和屈服位移。
(3)确定等效单自由度系统的地震需求。首先判断桥墩是否进入非弹性阶段,若交点的谱位移小于Dy*,说明桥墩处在弹性状态,该交点由式(4)返回求得需求点;若交点的谱位移大于Dy*,说明桥墩进入非弹性阶段,则按以下步骤对弹性需求谱进行折减:
1)计算等效弹性系统与弹性需求谱的交点得到Sae以及屈服点对应的谱加速度值Say,并求出延性折减系数Rμ=Sae/Say。
2)比较T*和Tc(地震动特征周期),按下式确定位移延性系数μ:

3)由式(7)得到非弹性需求谱。

式中:Sae和Sde分别是弹性谱中(伪)加速度值和位移值;Sa和Sd分别是非弹性谱的加速度值和位移值;T为周期。
4)计算非弹性需求谱与能力谱的交点,再由式(4)返回求出需求位移值。
为了检查桥墩地震需求的数据分布,进行了K-S检验,其原假设为各数据服从对数正态分布。图5给出了0.5 g时桥墩的位移延性需求值分布,可见,K-S检验的p值接近于零,因此数据不服从对数正态分布。
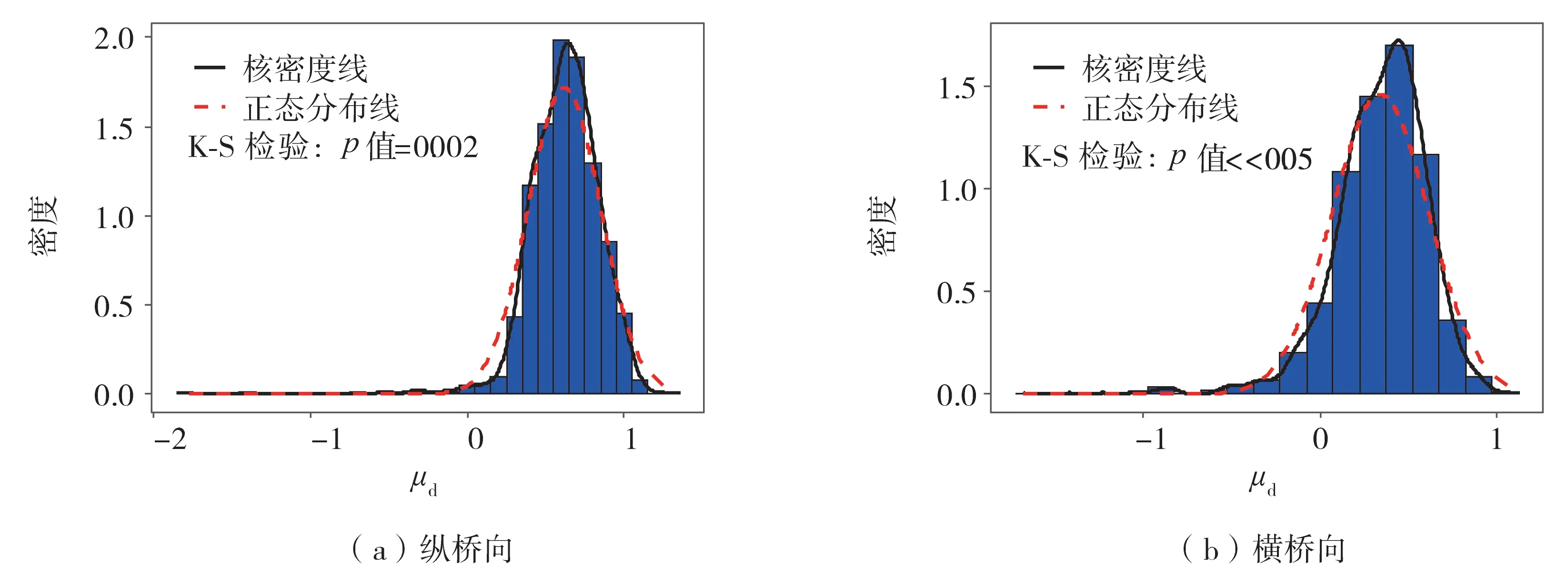
图5 PGA=0.5 g时桥墩的位移延性需求值分布Fig.5 Distributions of seismic demand for column displacement ductility at PGA= 0.5 g
传统方法通常采用Hwang 的建议以钢筋屈服、保护层混凝土剥落、钢筋拉断或核心混凝土压溃定义桥墩的损伤状态(DS),分别记为DS1、DS2和DS3,假定各损伤状态能力模型服从对数正态分布,对应的位移延性系数分别为1.0、1.76和4.76[21],其对数标准差取0.35[2]。表3显示了1 200个桥墩样本的屈服位移、各损伤极限状态位移延性系数的数据分布,采用K-S 检验桥墩的屈服位移和各位移延性系数是否满足对数正态假设,K-S检验结果表明,各损伤极限状态指标不能完全服从对数正态分布,且与建议值存在明显差异,倒塌状态位移延性系数明显低于建议值,且各位移延性系数的对数标准差随着桥墩损伤的变化而变化,未产生一致规律,更不是常值。所以,既有建议值是不适用于特定线路桥梁群组的桥墩性能。

表3 Pushover分析的桥墩损伤状态性能点Table 3 Performance points of pier damage states by Pushover analyses
3.2 双柱墩易损性分析
在传统的易损性方法中,地震动被缩放到相同的IM进行地震需求分析,得到构件需求值的概率分布,并与构件的能力模型进行卷积得到IM处的损伤概率,其易损性函数可写为:
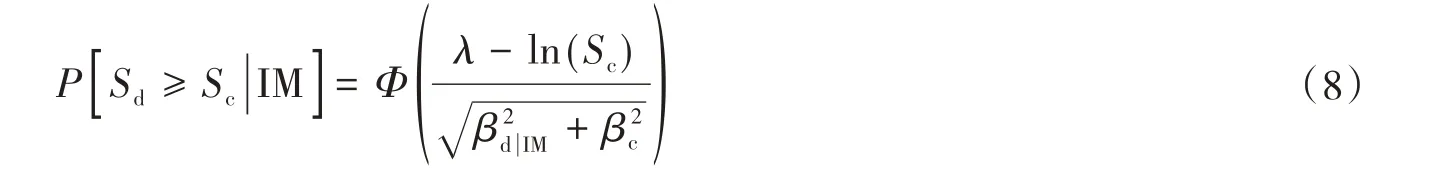
式中:P为在某级IM 下,指定损伤状态Sc下需求响应Sd的累积概率;λ为需求的对数均值。不确定性由需求响应的对数标准差(βd|IM)和损伤状态的不确定性(βc)决定。该方法能够计算每级IM 上的损伤概率进而生成易损性曲线。但是,该方法应在每级IM上的地震需求以及能力模型必须满足对数正态分布。考虑到传统方法中地震需求模型和能力模型的缺点,文中提出基于RF建立双柱墩易损性模型,步骤如下:
步骤1:使用LHS 生成双柱墩样本并建立有限元模型,对1 200 个样本在纵桥向和横桥向上分别进行Pushover分析。
步骤2:获取双柱墩的位移需求,以位移延性系数作为工程需求参数。
步骤3:训练RF 在对数空间中建立预测模型。将样本属性作为RF 的输入,比较步骤1 得到的各性能点对应的位移延性系数和步骤2 获得的位移延性系数,以找到桥墩所属的类,输出1 和0 的二进制向量分别表示桥墩响应超过和不超过各性能点阈值。
步骤4:基于输入变量的概率分布随机生成N个值(文中N取10万),使用各自的RF模型输出结果,计算失效概率P,即P=Nf/N,其中Nf为RF预测结果为1的个数。
步骤5:对各级IM重复步骤2到4建立易损性曲线。
文中采用PGA 作为地震动强度指标,输入RF 模型的桥梁属性包括主梁的跨径(L)和宽度(Dw),桥墩类型(Type),桥墩高度与截面直径之比(Ha·d)、横向柱高比(rh),系梁设置(Tieb),纵筋率(ρl)和配箍率(ρw),桩基的平动(KPT)和转动刚度(KPR),混凝土和钢筋的类型(Con、Ste)和强度(fcon、fste)以及上部结构质量系数(MF)。有盖梁桥墩和无盖梁桥墩分别记为A和B;根据系梁数量,将系梁设置记为a、b和c三类。由于桥墩的其他指标与上述指标具有相关性,所以,不作为RF模型的输入变量。
图6比较了使用传统方法和基于RF 的方法建立的桥墩易损性曲线,可以看出,对于DS1和DS2,与传统方法相比,RF 方法曲线在各级IM 上的斜率较大,说明易损性模型的标准差值较小,导致在地震动强度较小时,RF 模型的损伤概率小于传统方法的,但随着地震动强度的增大,传统方法将会低估桥墩的损伤概率;对于DS3,传统方法低估了桥墩的易损性。这说明直接采用对数正态分布假设和既有建议值建立特定线路桥梁群组的桥墩易损性模型会导致较大偏差,即传统方法对易损性模型的中值和标准差值均会产生偏差。

图6 传统方法和RF方法的易损性曲线比较Fig.6 Comparisons of fragility curves established by RF and traditional method
根据提出方法的步骤3,采用RF的分类精度表明RF算法准确分类的能力,精度定义为准确预测的数据与总数据的比[8]。由表4 得到,RF 易损性模型在各级IM 上的精度均在83%以上,具有较高的预测能力。此外,RF 并未对数据进行任何假设,相比于传统方法的对数正态性假设和能力模型的推荐值,RF 方法建立的易损性模型更具可靠性。

表4 RF模型的精度Table 4 Accuracy of RF models g
由于易损性函数在计算中比散点连成的折线更方便,可采用易损性均值和标准差值描述易损性模型。因此,使用正态累积分布函数拟合损伤概率点,获得特定损伤极限状态的平滑易损性曲线,拟合见式(9)。

式中,λ和β分别为桥墩达到指定损伤状态时,地震动强度(PGA)的均值和标准差。表5列出了3个损伤状态下桥墩易损性的均值和标准差值。可以看到,双柱墩横桥向的抗震性能优于纵桥向的,易损性均值和标准差值随着损伤的累积均增大。该易损性模型可直接用于研究线路桥梁中桥墩的损失估算。

表5 基于RF的双柱墩易损性模型Table 5 Fragility models of the double column piers using RF algorithm g
3.3 桥墩属性的相对重要性分析
分类模型除了计算特定IM下桥墩的损伤概率外,还可以用来快速识别损伤状态。若给出特定桥墩属性的参数值,则可以通过训练的RF模型快速判断桥墩在某地震动强度下的损伤状态,无须进行重复的有限元计算模拟。选择该线路中典型桥墩的参数配置,如表6 所示,RF 模型识别该桥墩在PGA 等于0.2、0.4、0.8 g时,分别处于桥墩屈服、保护层混凝土剥落和核心混凝土压溃状态。

表6 案例桥墩参数Table 6 Case pier parameters
根据式(2)计算RF 模型的GI降低值,由该值的最大最小归一化值[8]得出每个输入属性对桥墩易损性的相对重要性,图7 给出了各损伤状态3 种不同IM(PGA 分别为0.2、0.5、0.8 g)下输入属性的相对重要性,得到以下结论:

图7 桥墩属性对易损性的相对重要性Fig.7 Relative importance of the pier attributes on fragility
(1)桥墩的几何特性(Ha·d、rh)和类型对不同损伤状态的易损性有重大影响。
(2)属性的相对重要性随PGA 的变化而变化。例如,在DS1损伤状态,PGA 为0.2 g时,rh的影响重大,随着PGA的增大,Ha·d的影响更加明显。
(3)不同的损伤状态影响桥墩属性的相对重要性。由于桥墩非线性程度的发展,墩柱的类型、上部结构尺寸、配箍率等对易损性的影响会变大。
(4)纵、横桥向的重要属性具有差异。例如,DS3损伤状态,纵桥向的易损性对rh更敏感,横桥向则对Ha·d敏感。这主要是因为双柱墩在纵横向上产生损伤时的内力分布有关,在纵桥向,柱底是薄弱区;而在横桥向,不同类型的桥墩和系梁设置导致柱子的薄弱区的变化,双柱墩的盖梁根部以及系梁与柱子的节点区域是薄弱区,排架墩柱底的损伤则要远超于其他区域的损伤。
由于桥墩的类型、几何特性、上部结构尺寸、配箍率等是墩柱的内力分布以及损伤出现的位置和发展的显著影响因素,进而决定桥墩的易损性。
上述可见,基于RF的双柱墩易损性模型具有以下优点:(1)RF分类模型是非参数的,没有对桥墩的需求值和能力值进行任何假设;(2)在训练后的RF 模型输入特定桥墩的属性,可以快速识别桥墩的损伤状态;(3)在训练RF模型的过程中,可以确定影响易损性的重要属性。
4 结论
文中介绍了利用随机森林算法建立特定线路中小跨径梁桥群组的双柱墩的易损性模型的方法。考虑了桥梁的结构、几何和材料属性的不确定性,根据统计分布和拉丁超立方抽样对线路桥梁的双柱墩进行参数化表征,批量建立了有限元模型,并与传统条带方法对比,结论如下:
(1)提出基于RF建立双柱墩易损性模型的步骤。采用Pushover分析和能力谱法计算桥墩的地震需求和能力值,由随机森林建立输入的桥梁属性和输出1和0的二进制向量之间的易损性模型,该模型具有较高的预测能力,克服了传统方法中对数正态性假设和失实的能力模型建议值的应用。
(2)经过训练的RF 模型可快速地估计线路桥墩的损伤概率,并且在各级IM 上的精度均在83%以上。此外,若给定桥墩的属性参数值,则可以快速识别桥墩的损伤状态,避免重复的有限元计算,提高效率。
(3)相比于以单参数IM 建立的易损性曲线,在训练RF 模型的过程中根据GI 的降低可直接得出桥梁输入属性的重要性,结果表明几何特性和类型、上部结构尺寸、配箍率对本线路桥墩的易损性具有显著影响。
由于该模型是完全基于指定线路建立的,因此,文中之外的桥梁样本使用该模型时需要注意,应进一步根据提出的研究步骤训练和评估RF模型在其他线路桥墩中的性能。
