比对作战试验的定序指标考核研究*

薄 云，廖学军，白 宇

（1.航天工程大学研究生院，北京 101416；2.中国白城兵器试验中心，吉林 白城 137001；3.航天工程大学航天装备保障系，北京 102206；4.国防大学联合勤务学院，北京 100858）

0 引言

作为实战化导向在武器装备试验鉴定领域的具体体现，作战试验通过组织典型作战人员在模拟的作战行动中操控拟订购的武器装备，以实战的标准考察武器装备对于既定任务的完成程度和适用程度，为管理部门决策是否批量订购武器装备提供了最为公正客观的数据参考。已有的理论研究和工程实践一般认为作战试验应按如下过程组织，即：基于研制总要求和试验鉴定总案构建作战试验的指标体系和作战想定，并据此设计试验科目；通过执行这些科目采集数据；最后通过比对数据处理结果与指标体系中各指标的具体要求，以提供是否批量采购该武器装备的决策参考。简言之，该过程的组织逻辑是对照指标要求，考察作战表现。

然而，武器装备订购的初衷往往是为了更新换代现役装备。那么，必须明确的一个问题是：“相比于现役装备，拟订购的武器装备究竟能在多大程度上提高作战能力？”而回答该问题最自然的试验逻辑是直接比较两代装备在同等条件下的作战表现，也就是比对试验的试验逻辑。这在制药、医疗、工业、社会管理等多领域得到了广泛应用。虽然我军在作战试验领域还没有相关经验，但是美军已开展了大量的相关实践，比较有代表性的是Stryker 旅的作战试验。该试验在相同的作战条件下比较了Stryker 旅与轻型作战旅（被称为基线作战力量）几乎所有的考核指标，以最为直观的方式鉴定了Stryker 基于增强的移动性与态势感知能力而带来的作战能力的显著提升。

鉴于统计学对于试验鉴定工作的基础性支撑作用，并考虑到定量指标考核的相关方法，如t 检验、秩和检验、ANOVA 等在试验鉴定工作中已得到广泛应用，而定性指标考核还存在一些有待改进的方面，本文剖析了当前作战试验关于定性指标考核的普遍认识；讨论了基于ridit 统计方法考核定性指标的理论框架，并针对ridit 与分布无关，虽有利于操作和结果解释，但却不利于估算样本量的特性，研究了基于蒙特卡洛仿真的样本量估算方法；最后，通过算例演示了该理论框架和样本量估算的有效性，从而可为后续作战试验的组织实施提供有益参考。

1 作战试验定性指标考核现状

考虑到作战试验如何考核定性指标的过程实际反映了试验人员对于定性指标本质的认识。而该认识势必会影响到数据模型、统计技术与评估方法的选择。因此，本节概述当前作战试验考核定性数据的普遍做法，并指出可应用于比对试验的可改进的方面。

1.1 普遍做法

定性指标按其性质可分为3 类。其一是“是否”类指标，如“满意-不满意”、“适用-不适用”等，它的取值有两个，彼此之间有对立的关系；其二是“定序”类指标，如“差- 中- 良- 优”、“无效- 影响-轻伤-重伤-摧毁”等，它的取值一般有多个，彼此之间有程度的差别；其三是“名义”类指标，如弹药类型的“穿甲弹、破甲弹、爆破弹”等，它的取值一般有多个，彼此之间没有对立关系和程度差别。在当前作战试验中，应用最广的是是否定性指标和定序定性指标，简称为“是否指标”与“定序指标”。其考核的一般做法为：

在数据建模方面，主要将第一类定性指标转化为第二类指标，如：把“满意-不满意”转化为“满意度1-满意度2-…-满意度5”，其中，“满意度1”表示“最不满意”，“满意度5”表示“最满意”。然后，统一使用次序类指标的数据建模方式，通行的做法，是以1～5 或1～7 的自然数分别代表最低级别到最高级别的次序。

在数据采集方面，主要是以问卷调查的方式，问询作战试验中操控武器装备的作战人员。

在数据处理方面，主要是根据收回的问卷，对所有问询的结果进行加权平均，然后，以加权平均值作为该定性指标的考核结果。

在结果推断方面，主要是直接比对上述加权平均值与指标的规定要求。例如：指标要求满意度需大于80%，而问卷调查结果的加权平均值为82%，则认为该指标，即满意度达到规定要求。

1.2 可改进的内容

可以看出，该作战试验考核定性指标的过程尽可能真实地反映了作战人员关于被试武器装备的态度和评价，所以据此也能够比较公正客观地提出鉴定和采购的决策建议。但从数据科学的角度分析，该考核过程存在一定的改进空间。

一是以形如1～5 的连续自然数的方式将不同等级的定性数据定量化可能存在过度的人为界定。例如以1～5 分别代表“无效”、“影响”、“轻伤”、“重伤”、“摧毁”等5 个等级的打击效果。那么潜在地就认为“影响”到“无效”，“轻伤”到“重伤”的打击效果的跨度是一样的，或是“影响”是“无效”的打击效果的两倍。其他等级之间的跨度关系与倍数关系也与此类似。显然，这种界定往往是与现实不符的。

二是通过比较加权平均结果与指标规定以判定该指标是否通过考核的方式存在一定的出错概率，例如，被试武器装备的某定性指标实际水平低于指标规定，而作战试验中抽取的作战人员却普遍给出了该指标比较高的评价，那么根据其加权平均值得出该指标应通过考核的决策即是错误的。当然，对于任何决策来说，都存在出错概率，但以加权平均值判定考核结果的方式更为严重的问题是，它难以控制出错概率。

三是该考核过程通常只能依据试验资源的可用水平来估算样本量。而对于武器装备试验鉴定这样重要的工作来说，显然结论的重要性不言而喻，但是该考核过程却难以回答“为什么要试这么多次”，以及“如果多试××次，结论的可靠性将提高到××水平”等等这样的问题。

2 基于ridit 考核定性指标的理论框架

从数据科学的角度来分析，上述问题主要是当前过程未反映出试验的随机化本质，未从概率的角度考核指标。一般而言，可以把定性指标中的定序指标转化为是否指标，然后都以二分检验把定序指标转化为通过率的问题，可以实现上述改进。但某些定序指标非常难以转化为是否指标，例如：难以根据客观标准，把打击效果这个指标从“影响”到“摧毁”的5 个等级转化为“有”和“无”两个等级。另外，可以看出，当某些定序指标转化为是否指标之后，失去了更加细分的一些信息。因此，有必要研究如何为定序指标的考核实现上述改进。

2.1 原理概述

Ridit（relative to identified distribution unit）是一种非参数检验的分析方法，也即“参照指定分布单位的分析”。它的基本思想是把待考核的定序指标看作连续变量的一种近似，但这个连续变量无法直接测量，所以使用定序指标来反映该变量的各个级别，即以有序指标的各个级别对应该连续变量的各个区间。这些区间的长度未知，甚至各自的长度也有所不同，但认为其彼此相互衔接，如图1 所示。

图1 定序指标与对应连续变量的关系

正是由于这些区间的长度未知，所以当前作战试验使用连续自然数对其量化存在过度认为界定的问题。为避免该问题，Ridit 分析很巧妙地定义了一个ridit 得分的概念，它以参照分布的累计概率反映定序指标背后的连续变量本质。如图2 所示，假设定序指标的考核已经有了一个参照组，按照顺序计算各个级别的经验累计分布（empiricalcumulativedistribution），得到图2 中的阶梯曲线，然后认为每一阶梯的中点正好对应未知连续变量在该点累计概率的值，即图2 中的阶梯曲线与经验累计概率函数（ecdf）曲线正好在该点相交。该交点值即为ridit 值。以各级别指标在每组数据中的出现频率为权重，对ridit 值做加权平均，即可得到每组数据的ridit 均值。然后，利用该均值为基本依据，可作各组数据之间比较的假设检验，从而更进一步，避免当前定序指标考核无法控制决策风险的情况。最后，从控制假设检验出错风险的角度出发，可以科学计算出试验所需的样本量，从而避免了上述在当前定序指标考核中存在的第3 个问题。

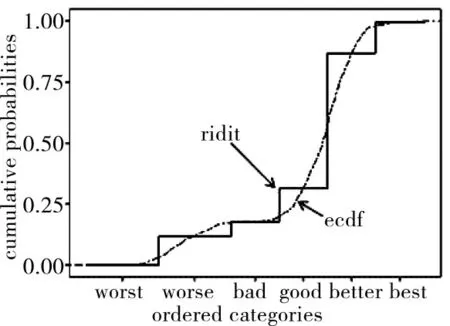
图2 ridit 值与连续变量累积分布的关系

另外，从ridit 均值的推导过程可以看出，任意两组结果的ridit 均值做差值并加上0.5 之后，如果结果为正数p，则表示前一组结果以概率p 由于后一组结果；反之则以概率p 劣于后一组结果。这就表ridit 分析不仅能够评断不同组结果的优劣，还以概率的形式明确反映了这种优劣的程度。这是当前定序指标考核方法难以做到的。

2.2 操作方法

Step 1：以参照组，也就是基线作战力量的定序指标考核结果计算ridit 值。具体计算过程如下页表1 所示，即（0）列出基线作战力量各级别的频数；（1）计算各级别频数的一半；（2）计算各级别之前的累积频数，其中最低级之前的累积频数为0；（3）计算（1）和（2）列对应值的和；计算ridit 值，即（3）列对应值除以频数总和，即基线作战力量关于该指标的问卷数总和。

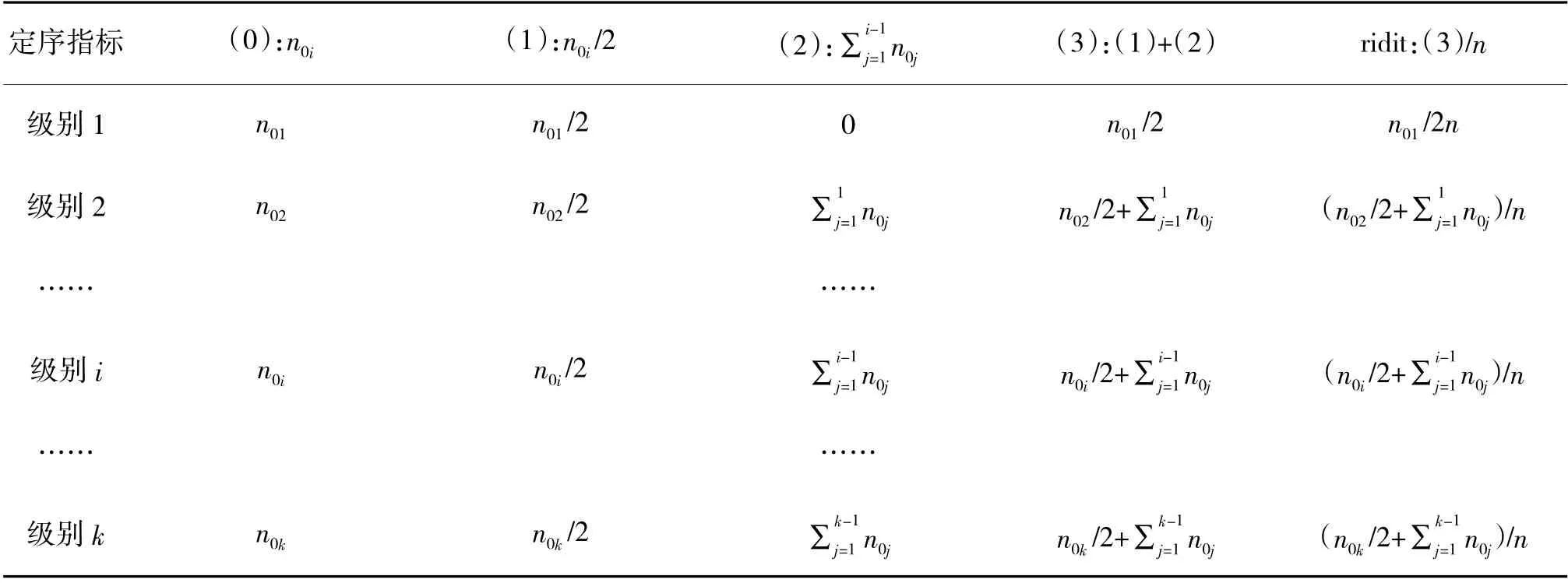
表1 ridit 值的计算过程表

Step 2：计算被试武器装备的ridit 均值，即：

Step 3：做假设检验：根据假设检验的一般原理，如果被试武器装备没有显著提升作战能力，那么被试武器装备该指标的问卷结果应与基线作战力量的没有显著差别，即二者的结果分布相同。而如果在此前提下，出现被试武器装备问卷结果或者更加极端的情况概率极低，那么这种前提条件就非常可疑，故认为二者分布有显著差别，即被试武器装备在该指标方面取得了显著提升。

参照文献［18］的论述，可按如下方法对该指标做假设检验为：

在0.05 的显著性水平下，当z 大于1.64 即认为被试武器装备在该指标方面得到了显著提升，否则，认为被试武器装备和基线作战力量在该指标方面没有差别。

2.3 样本量估算

从数据科学的角度估算试验的样本量，主要是从假设检验的原假设和备择假设的分布出发，以显著性水平和统计功效控制假设检验的两类错误为目的，从而以解析的方法精确求解试验样本量。可以看出，ridit 分析虽然有操作方便和结果解释性强的特点，但它与分布无关，因此，无法利用解析方法精确求解器样本量，只能使用蒙特卡洛等仿真的手段估算其样本量。具体可参照如下过程实施：

Step 1：根据历史数据或相近武器装备的数据，构建被试武器装备与基线作战力量的经验概率分布率，记定序指标的级别数为k；

Step 2：设定试验的显著性水平α、统计功效（1-β）和仿真的循环次数m；

3 算例演示

设待考核指标为毁伤效果，其级别数为7，根据基线作战力量的历史数据和被试武器装备在研制试验的相关数据如表2 中括号外数值所示。

表2 相关历史数据及其分布律

首先估算试验样本量：

Step 1：根据表2 计算基线作战力量与被试武器装备毁伤效果的经验分布律，如表2 括号内数值所示：

Step 2：设定试验的显著性水平α=0.05、统计功效（1-β）=0.80 和仿真的循环次数m=500；

Step 3：设定初始样本量n=7；

图3 样本量计算过程演示

然后，以n=16 为样本量，做毁伤效果的比对试验。假设得到数据结果如表3 所示。

表3 模拟试验数据及ridit 分析结果表

Step 1：以参照组，也就是基线作战力量的定序指标考核结果计算ridit 值，如表3 第2 列括号内数值所示；

Step 2：计算被试武器装备的ridit 均值，其结果如表3 合计栏中括号内第1 个数值所示；

Step 3：做假设检验并作结果解释：首先计算被试武器装备ridit 均值的标准差，其结果如表3 合计栏中括号内第2 个数值所示；其次计算统计量z的值为3.64，由于z 大于0.05 显著性水平下的临界值1.64，故得出结论“被试武器装备的毁伤效果指标在显著性水平为0.05 的情况下，显著优于基线作战力量；由于其ridit 均值为0.869，故被试武器装备在毁伤效果方面以0.869 的概率优于基线作战力量”。

4 结论

本文针对我军未来可能采用比对形式开展作战试验的实际情况，基于ridit 分析构建了作战试验比对试验中定序数据的考核框架，并给出了该类试验估算样本量的方法，通过算例演示可以看出：

1）相比较于当前定性指标考核中存在的人为过度界定的情况，基于ridit 分析的定序指标考核框架使用基线作战力量的累积概率分布作为定序指标的各级别赋值，更加科学严谨；

2）通过算例演示可以看出，基于ridit 分析的定序指标考核框架操作并不复杂，但利用显著性水平和统计功效可以很好地控制结论的出错概率，尤其是依据ridit 均值可以明确回答被试武器装备优于（或劣于）基线作战力量的概率水平，这是当前定性指标考核直接比较加权平均值与指标要求的做法无法比拟的；

3）通过算例演示同样可以看出，基于蒙特卡洛仿真估算该考核框架的试验样本量的核心在于构建经验概率分布率，因此，丰富的验前信息对于试验的组织是非常重要的，可以想见，验前信息越丰富越准确，样本量的计算会越准确，试验的综合效益也会越高；

4）本文论述的考核框架针对的是一对一的被试武器装备与基线作战力量，但稍作调整，该框架及其样本量估算方法可以扩充为一对多的被试武器装备与基线作战力量的比对试验，因此，可为我军未来该类型试验起到很好的决策参考；

5）本文讨论的是定序指标的考核问题，即关注如何评判武器装备单项指标的通过情况。当前作战试验在完成各单项指标考核之后，通常还需评估武器装备的总体或某一方面能力。很显然，前者是后者的基础，但两者并不完全等同。前者主要基于统计学中的假设检验，回答指标的“通过与否”；后者主要基于决策理论的效能评估方法，回答能力的“优秀程度”。在实践中，需加以把握。