45°特殊角的存在性处理策略

吴琼

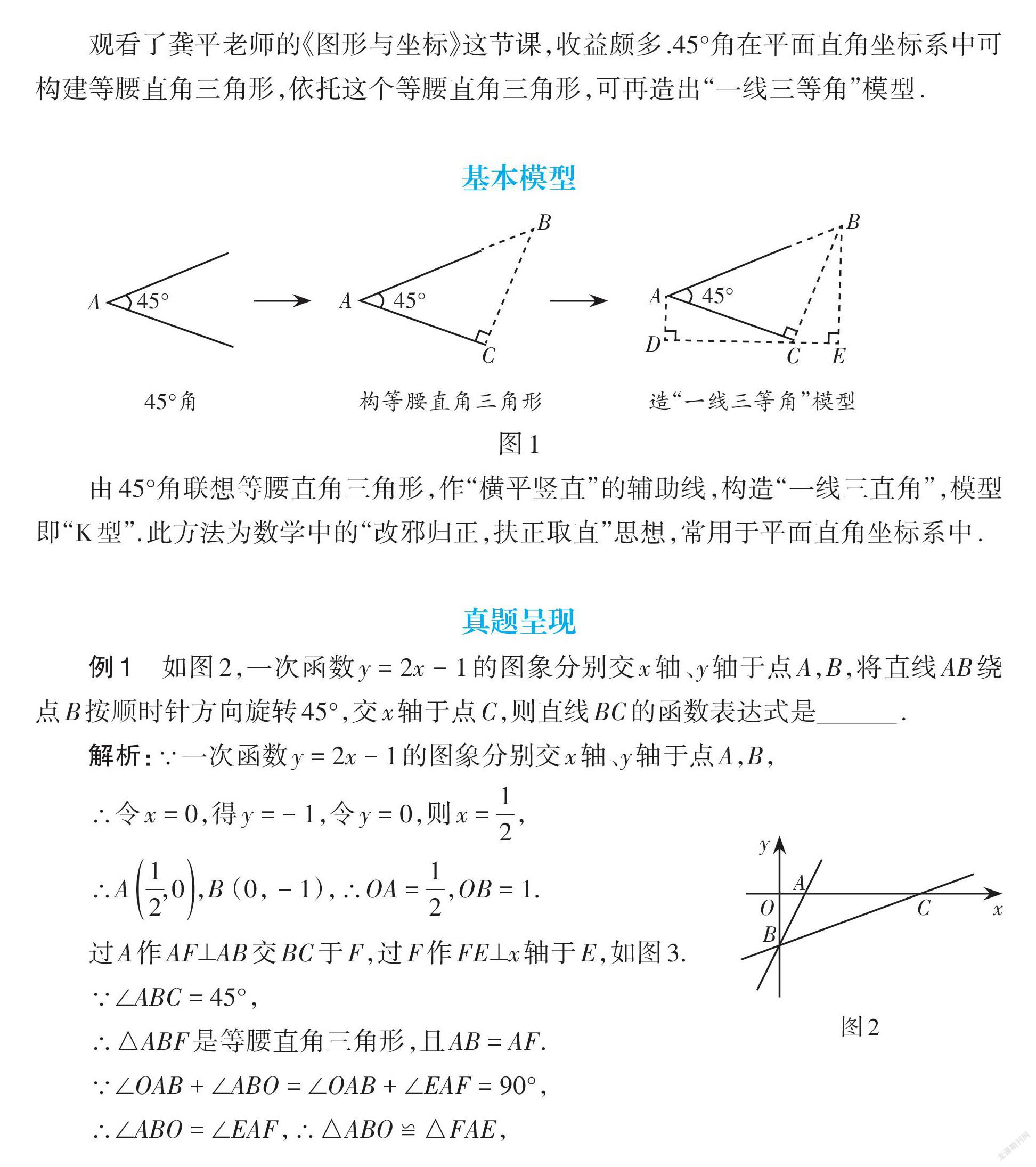
观看了龚平老师的《图形与坐标》这节课，收益颇多.45°角在平面直角坐标系中可构建等腰直角三角形，依托这个等腰直角三角形，可再造出“一线三等角”模型.

基本模型

由45°角联想等腰直角三角形，作“横平竖直”的辅助线，构造“一线三直角”，模型即“K型”.此方法为数学中的“改邪归正，扶正取直”思想，常用于平面直角坐标系中.

真题呈现

例1 如图2，一次函数y = 2x - 1的图象分别交x轴、y轴于点A，B，将直线AB绕点B按顺时针方向旋转45°，交x轴于点C，则直线BC的函数表达式是     .

解析：∵一次函数y = 2x - 1的图象分别交x轴、y轴于点A，B，

∴令x = 0，得y = - 1，令y = 0，则x = [12]，

∴A [12，0]，B （0， - 1），∴OA = [12]，OB = 1.

过A作AF⊥AB交BC于F，过F作FE⊥x轴于E，如图3.

∵∠ABC = 45°，

∴△ABF是等腰直角三角形，且AB = AF.

∵∠OAB + ∠ABO = ∠OAB + ∠EAF = 90°，

∴∠ABO = ∠EAF，∴△ABO ≌ △FAE，

∴AE = OB = 1，EF = OA = [12]，∴F [32，-12].

设直线BC的函数表达式为y = kx + b，

∴[32k+b=-12 ，b=-1，]∴[k=13 ，b=-1，]

∴直线BC的函数表达式为y = [13]x - 1.

故应填y = [13]x - 1.

变式延伸

例2 如图4，一次函数y =  - 2x  -  2的图象分別交x轴、y轴于点A，B，将直线AB绕点B按顺时针方向旋转45°，交x轴于点C，则直线BC的函数表达式是     .

解析：由题意可得A（ - 1，0），B（0， - 2），

∴OA = 1，OB = 2.

过A作AF⊥AB交BC于F，过F作FE⊥x轴于E，如图5.

∵∠ABC = 45°，∴△ABF是等腰直角三角形，且AB = AF.

∵∠OAB + ∠ABO = ∠OAB + ∠EAF = 90°，

∴∠ABO = ∠EAF.

∵∠AOB = ∠AEF，∴△ABO ≌ △FAE（AAS），

∴AE = OB = 2，EF = OA = 1，∴F（1，1）.

设直线BC的函数表达式为y = kx + b，

∴[k+b=1，b=-2，]解得[k=3，b=-2，]

∴直线BC的函数表达式为y = 3x - 2. 故填y = 3x - 2.

分层作业

难度系数：★★★  答题时间：10分钟

如图6，一次函数y = 2x + b经过M（1，3），它的图象与x轴、y轴分别交于A，B两点. 将该直线绕点A顺时针旋转45°至直线l，过点B作BC⊥AB交直线l于点C，求点C的坐标及直线l的函数表达式.

（答案见第33页）

（作者单位：辽宁省大连市第三十七中学）