永磁同步电机GWO-PID优化控制

张俊杰，李昕涛

（太原科技大学电子信息工程学院，山西太原，030024）

0 引言

永磁同步电机具有结构简单、响应速度快等优点，在电动汽车和工业设备等领域得到了广泛关注与应用。但PMSM的参数易受环境影响，如温度变化会引起定子电阻和磁链变化、磁饱和会引起dq轴电感变化等，从而导致 PMSM 驱动系统性能下降。因此，为了达到高性能电机控制的目的，获得精确的电机参数和数学模型对改善 PMSM 的控制性能至关重要[1]。

控制系统中传统参数辨识方法，通过文献分析可知，这些方法均有利有弊，其中突出的一个缺点是这些方法并未考虑PMSM本身的非线性因素，导致辨识精度受到一定的影响[2]。而群智能优化算法凭借其考虑到问题非线性影响的特点，在PMSM参数辨识中得到了广泛研究与应用。采用群智能优化算法进行参数辨识已成为目前重要的解决方案之一。

研究人员通过对大自然的观察仍在不断提出新的优化算法，例如学者Seyedali Mirjalili通过对大自然中肉食动物捕猎的观察提出灰狼优化算法(grey wolf optimization algorithm，GWO)。在函数优化方面，已经证明GWO的收敛速度和求解精度均优于PSO。因此，GWO算法广泛应用于无人作战飞行器路径规划、聚类分析、特征子集选择、经济调度指派、直流电机最优控制、多输入多输出电力系统等诸多领域[3]。由于GWO算法提出的时间不长，因此其理论研究尚未成体系，多数学者都是从特定角度，针对具体问题对GWO进行改进和应用研究。灰狼优化算法模型简便、可实现性强，在诸多领域的优化表现不亚于其他元启发式群智能算法。本文将选择该算法进行改进，并在多参数辨识中得到了实际运用。课题组以永磁同步电机系统转速为研究对象，将灰狼优化算法（GWO）与PID控制器互相结合，并在Simulink中由GWO-PID在线对系统进行辨识，根据辨识得到的灵敏度信息整定 PID 控制参数，最后通过仿真验证了该方法的有效性。

1 永磁同步电机模型

永磁同步电机主要的部件是定子、转子、端盖。定子部分由电枢铁心和三相对称电枢绕组二部分组成，通过叠片的方式来减少电机运行时的铁损，与普通感应电机无太大区别。其中铁心槽中嵌着电枢绕组。转子是由导磁轭、转轴、永磁体构成的。导磁轭往往是以圆筒的形状，并套在轴上的，与此同时紧贴着永磁体。在定子与转子之间存在一段气隙部分，转子在定子部分内的旋转运动所需要的空间由此气隙部分所提供。很多电磁过程和参数的研究主要发生在这一区域，所以该气隙部分作为一部分内部结构，其形状、长短均会影响永磁同步电机的力学、电磁性能，而且还与电机的杂散损耗与工艺装配相关。就永磁同步电机而言，转子中永磁铁因其安装部位的差异而产生的磁路结构也有差异，电机有类别主要有三种：内埋式、凸装式、嵌入式。

在d-q坐标系下的永磁同步电机系统，其数学模型为:

电压方程:

式中:Ud和Uq分别为d轴和q轴上定子电压分量，Rs为定子电阻，id和iq分别为d轴和q轴上定子电流分量，Ld和Lq分别为d轴和q轴上定子电感分量，ω为转子机械角速度，Øf为永磁体磁链，p为极对数。

电磁矩阵方程：

式中Te为电磁转矩。

电磁转矩方程在有负载的情况下与负载转矩还应满足:

式中:TL为负载转矩，J为转动惯量，B为摩擦因数。

为了实现d轴和q轴的电流静态解耦，矢量控制时 id= 0，所以式(5)可以简化为:

由上述式子可以看出，永磁同步电机的数学模型具有非线性，并且和负载转矩关联性强。在永磁同步电动机中，存在着一种具有电磁场的相互联系，其电磁场的微分方程一般为含有一系列可变因子的微分方程，而系数是以时间为变量的函数并根据转子与定子相对位置而变化。一方面，转子与定子的位置变化是非线性的，而且微分方程的变量包括定子电流、转子磁链等。永磁同步电机是非线性多变量系统的一种。另一方面，定子和转子之间的耦合关系由磁场决定，在一般坐标系中，电机定转子在电磁结构上的不对称性，使得电机数学模型可以从由转子瞬时位置所形成的非线性时变方程进行转变。所以在对同步电机控制系统进行精准分析与研究往往比较困难，需要对同步电机进行一些细节理想化处理，并根据不同的需求来选择应用其中一种模型或是结合每一种模型的优点综合化分析处理。

忽略以下干扰条件：（1）磁路饱和、磁滞、涡流；（2）永磁体的阻尼作用、转子中的阻尼绕组；（3）磁路中的高次谐波磁势。

遵循以下条件：（1）电动机的磁回路是线性的，利用叠加理论对电动机的磁力参数进行计算；（2）在各自的绕组轴线上有120的电角度差异的三相对称的定子绕组；（3）气隙磁路中定子电流仅发生正弦磁势，而定子电位为正弦形变化；（4）三相绕组采用Y形的定子绕组，并采用正弦波形的相绕组的感应电位；（5）定子气隙处的永久磁铁的磁场强度为正弦形；（6）铁芯具有无限大的磁导率，而转子永磁体的导电系数为0；（7）电机运行时所有绕组电感及电阻等参数恒定；（8）永磁体内部磁导率等于空气。

2 灰狼优化算法

GWO算法的灵感来源之一是狼群社会等级分布。狩猎灰狼群体一般为5～12只，为了体现出灰狼社会等级的分布，将最优解定义为ɑ狼，依次按β、δ、ω的顺序排列。整个灰狼群体由а狼指挥，它又称为领头狼，负责狼群各项事宜决策;β狼又称为副领头狼，听从ɑ狼命令，辅助ɑ狼进行决策，管辖除ɑ狼以外的其他狼；δ狼被称为普通狼，服从ɑ狼和β狼命令，在狼群中起到放哨、侦察等作用；ω狼被称为底层狼，它等级不高但数量多，听令于上面3个等级的灰狼。狼群位置主要由ɑ狼和β狼指挥，整个狼群的位置随ɑ狼的位置更新。灰狼狩猎分为3个步骤:首先，狼群搜索猎物；然后，ɑ狼带领狼群包围猎物；最后，在狼群慢慢靠近猎物过程中，逐步缩小包围圈，ɑ狼指挥其余狼发起攻击，不断更新包围圈里狼群位置。

灰狼围猎的数学模型为

式中:t为当前迭代次数;X为灰狼所处位置;Xp为猎物所处位置;A为包围步长;C为方向向量，计算公式为:

式中r1和r2为［0，1］之间的随机向量。灰狼捕猎的位置更新公式为:

式中:X1、X2和X3分别表示狼群中ω向α、β、δ移动的步长和方向;X(t+1)定义了最终位置即表示其余灰狼ω向猎物移动的方向。

灰狼能够识别猎物的位置并包围它们。当灰狼识别出猎物的位置后，β和δ在ɑ的带领下指导狼群包围猎物。在优化问题的决策空间中，我们对最佳解决方案（猎物的位置）并不了解。因此，为了模拟灰狼的狩猎行为，我们假设ɑ，β和δ更了解猎物的潜在位置。我们保存迄今为止取得3个最优解决方案，并利用这三者的位置来判断猎物所在的位置，同时强迫其他灰狼个体（包括ω）依据最优灰狼个体的位置来更新其位置，逐渐逼近猎物。狼群内个体跟踪猎物位置的机制。

GWO算法的优化从随机创建一个灰狼种群(候选方案)开始。在迭代过程中ɑ、β和δ狼估计猎物的可能位置（最优解）。灰狼根据它们与猎物的距离更新其位置。为了搜索过程中的勘探和开发，参数a应该从2递减到0。如果｜A→｜＞1，候选解远离猎物；如果｜A→｜＜1，候选解逼近猎物。GWO算法流程图如图1所示。

图1 灰狼优化算法的流程图

3 系统仿真

本节通过GWO算法在电机参数辨识中的辨识效果来验证融合后的算法相较于无算法的PID控制具有更高的精度和更快的速度。本次算法需将迭代次数设置为100，用以获得最优参数值，种群数量设置为50，故迭代一次系统需运行五十次寻求单次迭代最优值。在仿真实验中，使用Matlab中的Simulink，建立辨识仿真图，如图2所示。仿真实验空载情况下的转速曲线图如图3，转矩曲线图如图4，电流曲线图如图5。仿真实验结果带负载转速曲线图如图6所示，转矩曲线图如图7所示，电流图如图8所示。

图2 系统Simulink仿真模型

图3 空载转速曲线

图4 空载转矩曲线

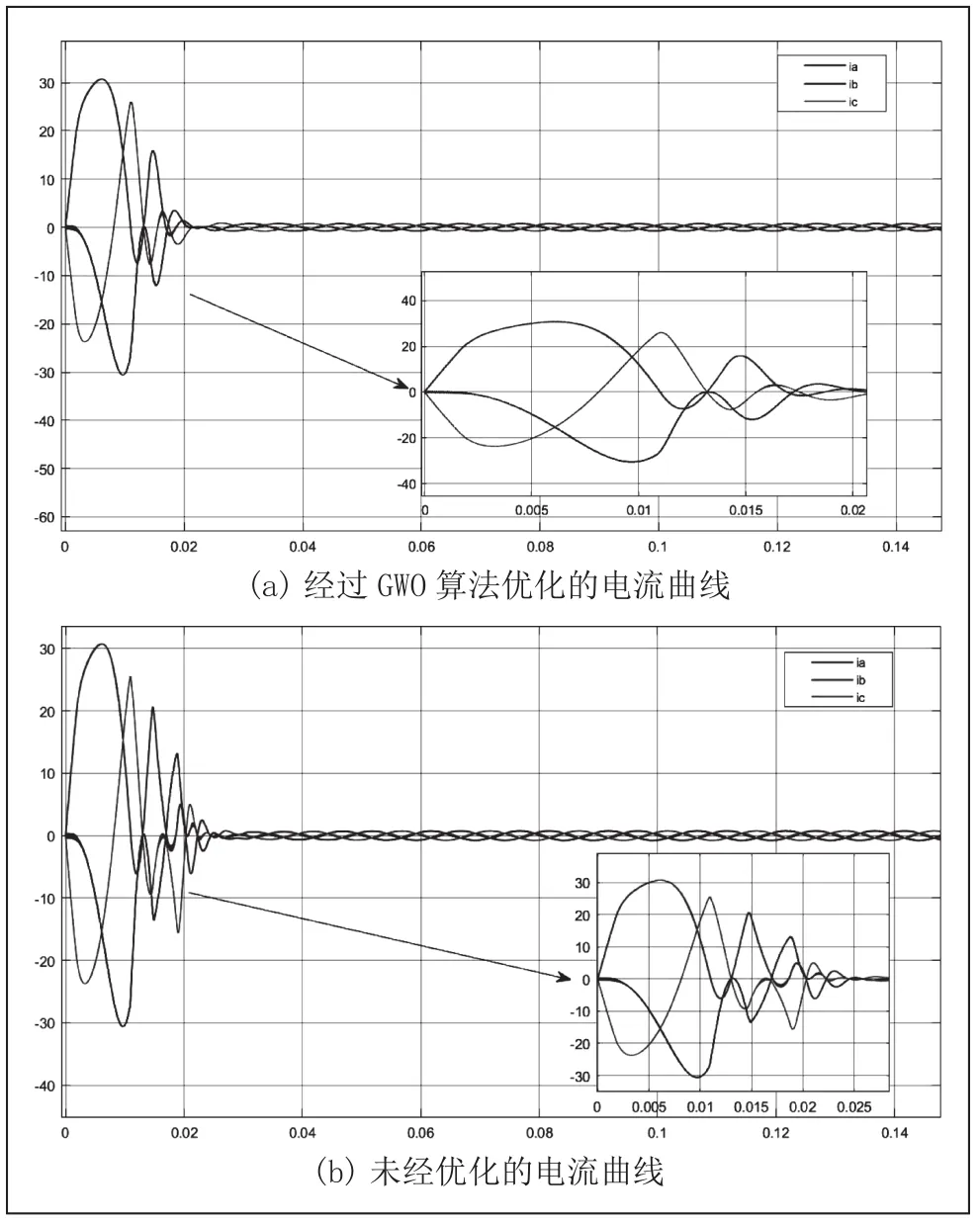
图5 空载三相电流曲线

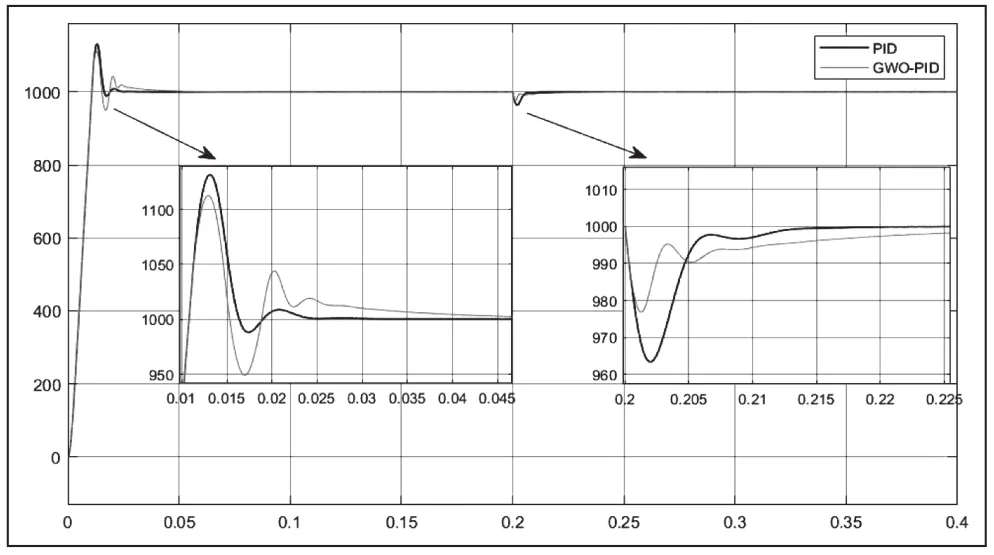
图6 带负载转速曲线

图7 带负载转矩曲线

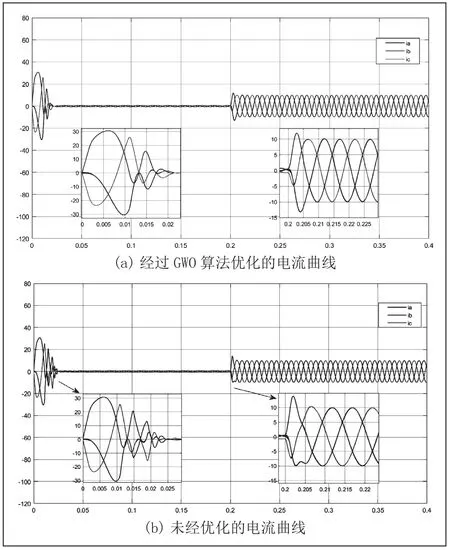
图8 负载三相电流曲线

4 结语

永磁同步电机控制系统由于其具有高效、简单、易控的特点在现代工业生产中应用得愈发广泛。另一方面，完整高效的控制系统的运行需要精准的参数以支撑，而永磁同步电机处于运行状态中其重要参数会因为某些不可抗拒的因素而有所偏差，所以选择适当的辨识方法来精准地估计此类变化的参数是非常有必要的。针对永磁同步电机矢量控制系统，课题组设计了基于灰狼优化算法(GWO)的 PID 控制器，根据优化算法的辨识的灵敏度信息对 PID 参数进行再整定，通过在 Simulink 中进行仿真验证基于GWO优化算法的 PID控制器控制效果更好。并且GWO算法的每次迭代的计算数量可以根据具体情况更改，算法复杂度较低，后续可以在嵌入式控制设备中进一步移植与应用。