数字信号处理技术在地基动力参数测试中的应用

2022-03-07孙锐

石油化工建设 2022年11期

孙锐

化学工业第一勘察设计院有限公司河北沧州 061001

动力机器的动荷载必然会引起地基及基础的振动，从而可能产生一系列不良影响。因此，动力机器基础设计应满足下列基本要求：不应产生影响机器正常使用的变形；基础本身应具有足够的强度、刚度和耐久性；不产生影响工人身体健康、妨碍机器正常运转和生产，以及造成建筑物开裂和破坏的剧烈振动；基础的振动不应影响邻近建筑物、构筑物或仪器设备等的正常使用。动力基础设计成功与否的关键步骤之一就是确定地基动力参数。

1 地基动力参数测试机理

对于实体基础振动计算，目前主要有质量- 弹簧-阻尼器模型理论及刚体- 半空间模型理论，我国目前工程多采用质量- 弹簧- 阻尼器的计算模型。质量- 弹簧- 阻尼器理论：假设基础为无弹性的质量，地基为无质量的弹簧，基础受垂直扰力Pssinwt 作用时，基础产生的惯性力与基础振动加速度成正比例，阻尼力与振动速度成正比例，地基的反力与振动位移成比例。其力学模型如图1 所示，公式见式（1）。

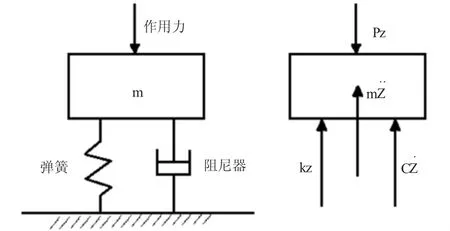
图1 质量- 弹簧- 阻尼器理论示意图

用质量- 弹簧- 阻尼器理论进行机器基础动力分析时，要提供地基土的地基刚度、阻尼比等动力参数，这需要在现场进行块体基础动力测试，以满足设计需要。一般做法是在现场浇筑模拟基础，在基础上安装激振器和拾振器，通过激振器对基础施加不同频率的激振力，通过拾振器测出对应的基础振幅。图2 为现场地基动力参数测试示意图。

图2 现场地基动力参数测试示意图

通过计算求出设计所需的动力参数。依据《地基动力特性测试规范》及《岩土工程勘察规范》及设计要求，数据处理应得到幅频响应曲线：竖向振动线位移随频率变化的幅频响应曲线；水平振动线位移随频率变化的幅频响应曲线，以及基础顶面测试点由回转振动产生的竖向振动线位移随频率变化的幅频响应曲线；基础顶面测试点在扭转力矩作用下的水平振动线位移随频率变化的幅频响应曲线。

2 行业现状

以往试验多采用仪器采集数据后人工量波的方法来获得幅频响应曲线。如果某一频率采集到的测试信号有8个极大值、8 个极小值，应该用8 个极大值的平均值减去8个极小值的均值，得到振幅；8 个极大值或极小值的长度即7 个波经历的时间，通过换算可以求得对应频率。当然也可用频谱分析方法求得频率。当频率改变，需要再重复这些步骤，依次获得幅频响应曲线。如果收集到的测试信号由更多数据形成，则数据处理量又会成倍增加。所以该手段费时、费力、误差大。另外，测试信号存在高频或低频干扰，如何准确确定频率及振幅也存在一些具体问题。再次，现场实际测试时，需要找到共振峰，但共振峰对应频率相对较高，测试基础振幅较大，数据较难获得。为减少人工量波数据计算中的劳动强度，提高计算精度和工作效率，需要通过数字信号处理技术来解决上述问题。

3 设计思路

数字信号处理主要包括数字滤波、数据截断、加窗、频域分析和奇异点剔除等。

3.1 滤波处理

对测试数据进行低频和高频干扰进行平滑滤波，提高有用信号的计算精度。

3.2 计算频率值

频率值计算的基本原理：利用信号傅立叶变换具有的信号时域与频域之间的对应关系，建立信号的DFT 与四种信号频谱之间的关系。

设时间域某一窗口宽度（采样数据个数）为N，采样频率为CYPL，则对该数据段作快速傅里叶变换，寻找幅度谱中的极值。设在N 个变换的数据中，第SK 值最大，则即可求得该数据段的振动频率，见式（2）。由式可知，频率域的采样精度与时间域的CYPL 成反比，与样本数N成正比。由于须满足采样定律，同时提高时间域的振幅精度，CYPL 不能太低，只能提高N 来提高频率域的频率精度，即在N 个采样数据两边补充0。假使将当前数据的频率精度提高10 倍，即需在N 个采样数据段前后各补充5N 个0。若对10N 个采样数据进行快速傅里叶变换，则计算量增加很多，降低了计算速度。因此，在程序设计时，先对N 个样本值作快速傅里叶变换，寻找极值SK。实际振动频率与SK 推算出的振动频率相差不大，只需对SK附近的几个数据作精确计算，作傅里叶变换，即可精确求得振动频率。这样即不影响计算速度，又提高了计算精度。

F=SK×CYPL/ N。 (2)

时间域窗口宽度N 相当于对信号进行加窗处理，即将信号乘以时域的有限宽矩形窗函数，采样后信号x(t)g(t)经截断成为x(t)g(t)w(t)，见式（3）。

由数值分析原理可知，信号截断会造成能量泄露问题，如余弦函数信号主频为f0，截断后经过傅里叶变换的幅度谱出现....- 3f0、- 2f0、- f0、f0、2f0、3f0……等多个极值用图形表示信号的截断、能量泄漏现象。提高截断信号长度，即提高矩形窗宽度可减小泄漏，此时sinc 函数主瓣变窄，旁瓣向主瓣密集，由于旁瓣衰减较快，故可减小泄漏。但显然采样点数随之提高，增加计算负担。此外，还可以采用其他窗函数。一个好的窗函数，其主瓣应尽可能窄（提高频率分辨力），旁瓣相对于主瓣尽可能小，且衰减快（减小泄漏）。几种典型窗函数的技术指标见表1。分析可知，汉宁窗是比较适宜的加窗函数，当然也可根据不同情况选择不同的加窗函数。

表1 几种典型窗函数的技术指标

3.3 计算振幅值

由已求出的该数据段振动频率，可求得振动周期。假使此数据段有n 个振动波段，分别对每个波段采用筛选法，寻找极大值、极小值和该振动波段的振幅；将n 个振动周期的振幅求平均值，即为该数据段的振幅值。

3.4 多窗口宽度

可将测试数据分为不同的数据长度：512 点、256 点、128 点和自动窗口宽度。自动窗口宽度是指在转换数据过程中窗口宽度并不固定，而是将上一数据段的10 个振动周期作为下一数据段的长度。此种方法的优点是在振动频率较高时，所获得的幅频响应曲线计算精度较高。

3.5 得到测试成果

依次对数据的各段作频率和振幅计算，从而得到幅频响应曲线，在幅频响应曲线上依据规范选取数值计算，即求得测试成果，如图3 所示。

图3 计算成果输出示意图

4 应用实例

应用以上思路编制了激振法测试数据处理系统软件，该程序于2001 年编制完成，先后在南京扬子乙烯扩建（桩基）、德州华鲁恒升大氮肥扩建（天然地基）内蒙神华煤液化（天然地基、桩基）和天津渤化石化有限公司60 万t/ a丙烷脱氢(桩基) 等工程中得到验证，取得良好的效果。2013 年，该软件通过国家版权局颁发的计算机软件著作权登记证书。