政府发展性支出、产业集聚与绿色能源效率

江 洪，李金萍，李秋雁

（辽宁工程技术大学工商管理学院，辽宁葫芦岛 125105）

一、引言

改革开放40 多年以来，中国经济持续稳步增长。在此过程中，为了发挥产业格局对经济增长的正外部性影响，中国区域经济尤其是工业行业呈现了不同水平的集聚性特征。Krugman（1991）和Fujita et al（1999）指出产业集聚对同一地区企业的正外部性影响主要通过技术外溢和知识扩散效应实现。然而，产业集聚并非单纯的市场行为，政府在此过程中发挥了不可替代的助力作用。O’Sullivan（2000）研究发现政府通过改善投资环境，吸引异地厂商投资，从而形成产业集聚。从能源利用角度，产业集聚过程中的技术外溢、基础设施共享等要素可以促进区域能源效率的提升。然而，长期以来中国经济的高速发展却伴随着能源消费的激增和环境负荷的加剧，产业集聚并未发挥节能减排的正面作用。

理论上以利润最大化为目标的产业集聚，如果在单纯的市场机制调节下应该能够实现优化配置，促进经济增长，提升能源效率。然而，在财政分权的体制下，由于地方政府目标异化导致旨单纯从地方政府利益出发而诱导企业投资行为的差异化政策租（信贷、补贴、税收减免等）的出现，进而诱发为追逐政策租而形成企业扎堆，而并非真正意义上的产业集聚。钱学锋等（2012）的研究发现，过度的政策租驱动会诱发重复建设和产业结构趋同，进而因资源配置扭曲导致市场分割，最终无法产生产业集聚应有的技术溢出和共享效应。政府在产业集聚中到底扮演怎样的角色，1936 年，凯恩斯（Keynes）在政府干预经济的理论中就阐述了政府对经济的干预行为在实现国家经济的稳健增长中的重要作用。后来，0orter（1990）利用钻石理论分析了产业集聚过程中政府行为的双重作用，政府的政策租行为会直接影响到钻石体系中的生产要素。一方面，适当的政策租可能成为产业发展的助力；另一方面，当环境发生变化时，政府行为可能成为产业集聚的阻力。

可见，过度的政府干预经济行为加速亦或扭曲了中国的产业集聚，为了实现产业集聚释放其应有的绩效，是否应该弱化政府干预，甚至让政府彻底退出。林毅夫（2008）认为，发展中国家最重要的制度便是政府，政府以外的其他制度及其质量均受政府政策的影响。中国经济高速增长和产业集聚过程中，政府是重要的推动力，政府干预有可能带来产业集聚应有的共享和外溢效应，推动能源效率的改善；但是，地方政府的目标异化及边界条件的模糊，也可能带来产业扎堆，无法发挥技术共享和外溢效应，阻碍能源效率的提升。解决政府干预与能源效率之间矛盾的最理想选择是，协调政府行为与市场机制之间的关系，使政府目标与其边界条件清晰化。

综上所述，本文尝试分析不同程度的政府发展性支出，是否会带来不同质量的产业集聚，进而以不同的方向和方式作用于能源利用效率，最终找到政府发展性支出的边界。以期进一步规范政府行为，实现真正意义上的产业集聚，发挥其技术外溢和共享效应，为区域能源效率提升提供政策启示。

二、文献综述

（一）能源效率评价的研究

国内外学者针对能源效率评价的研究主要从单要素和全要素两个视角展开。早期学者主要从能源强度、能源生产率等单要素视角着手，集中于偏要素框架，大部分研究都是分析能源消费与经济增长的关系（蒋金荷，2004；史丹，2006），而忽略资本、劳动等其他投入要素。为了完善能源效率评价指标体系和方法，Hu和Wang（2006）提出了全要素能源效率指标及其评价框架。该框架基于DEA（data envelopment analysis）数据包络分析模型，借鉴道格拉斯生产函数，将能源、劳动力、资本作为投入要素，GD0 作为产出要素，以能源消费实际值与目标值的比值作为能源效率的评价指标，在后来的能源效率评价研究中，该方法被广泛应用（Hu和Kao，2007；师博和沈坤荣，2013）。经济发展必然伴随着能源的消耗，而能源，尤其是传统化石能源消耗的过程中，必然带来污染物的排放，生态环境压力日益加重。鉴于此，众多学者尝试将能源消费过程中产生的污染物排放，纳入能源效率评价体系，保证能源效率的评价结果更加客观、科学（张三峰和吉敏，2014；江洪和纪成君，2020）。为了解释能源效率变动过程中内部因素的影响，部分学者运用DEA-Malmquist 指数法，将能源效率分解为纯技术效率、技术进步和规模效率，并进行跨时期比较（陈星星，2019）。能源效率变动不仅受内部因素的影响，外部环境因素也不可忽略。近年来，为了探索能源效率变动究竟是归因于内部管理还是外部环境，很多研究采用分阶段DEA 方法，先用传统DEA 方法测度能源效率，然后选取产业结构、人口密度、经济发展水平等外部环境因素，采用极大似然估计方法，对决策单元进行排序。通过调整能源的投入量，以达到决策单元处于同等外部环境，再用DEA 方法进行能源效率测算，最终解释能源效率变动归因于内部管理和外部环境的差异性（江洪和赵宝福，2015；吴江等，2019）。

（二）产业集聚对能源效率影响的研究

通过梳理以往的大量文献，大部分学者认为技术进步是能源效率提升的根本动因。技术进步主要通过直接作用（潘雄锋等，2017）和间接作用（钱娟和李金叶，2018）两种途径促进能源效率的提升。但也有一些学者认为短期内技术进步虽能够提升能源效率、促进经济增长，但长期看来，经济的快速增长将带来更多的能源消耗，从而对效率提升带来的延缓节约产生抵消作用，即技术进步的回弹效应（rebound effect）（胡秋阳，2014）。后来，部分学者开始研究产业结构变动对能源效率的影响。Denison（1969）和Maddison（1987）研究发现，能源要素根据生产率水平，从低水平行业或部门向高水平行业或部门转移，其在整个国民经济中的利用效率将得到提升，这也是“结构红利假说”的基本思想。该思想中，产业结构是通过外部性作用于能源效率，与产业外部性密切相关的现象就是产业集聚。关于产业集聚的研究早在20 世纪90 年代就开始兴起（Kim，1995），而外部性则被认为是产业集聚的重要诱因（Henderson，1974）。Marshall（1920）指出，产业地理集聚（agglomeration）的原因，很大程度上取决于其产生的外部性经济，包括技术外溢、娴熟的劳动力市场及专业的服务性中间行业。以此类推，生产尤其是工业生产过程中，能源是不可或缺的投入要素，本企业能源利用效率也可能受到其他企业能源利用技术的影响。王海宁和陈媛媛（2010）通过实证研究，验证了产业集聚的正外部性可以有效提高能源效率的假说。师博和沈坤荣（2012）研究发现，产业集聚借助规模经济、产业间的技术外溢及基础设施共享，为节能减排发挥积极效应。程中华等（2017）采用动态空间面板模型分析了产业集聚对能源效率的影响，发现无论是生产性服务业集聚，还是制造业与其共同集聚，都有利于区域能源效率的提升。师博和任保平（2019）研究发现，国有企业因政府有偏的干预目标而滋生道德风险，诱发地方政府和国有企业的双重预算软约束、导致资源错配，并且企业研发无法产生技术外溢以优化能源效率，抑制产业集聚释放节能减排潜力。邵帅等（2019）从理论和实证两个角度，分析了经济集聚对碳排放的影响，发现经济集聚通过其正外部性和能源强度，分别对碳排放产生直接和间接影响。

综上所述，国内外学者正对产业集聚如何影响能源效率进行了广泛的研究，并取得了丰富的成果，为本文的写作奠定了扎实的理论基础。然而，由于地级市层面能源消费量数据的缺失，前期关于能源效率测度的研究往往局限于省际层面；同时，能源效率影响因素研究过程中往往忽略政府行为，在财政分权和政绩考核背景下，政府行为已经成为影响资源配置的重要变量。为了弥补前期研究的不足，本文拟从以下几个方面寻求突破：其一，运用卫星夜间灯光数据，模拟测度地级市能源消费量，并将多种污染物作为非合意产出，运用SBM-Malmquist-Luenberger 指数法重新测算各地级市能源效率现状；其二，在产业集聚影响能源效率的分析中，加入政府发展性支出的门槛变量，探索政府行为在产业集聚影响能源效率过程中的边界，探索市场行为和政府行为共同提升区域能源效率的适当合力。

三、理论分析与研究假说

在长期的粗放型经济增长方式下，地方政府往往过度重视任期内的GD0 增速，而忽略经济可持续发展的长期增长因素，导致了经济短期内快速发展以过量的资源消耗和严重的环境负荷为代价。鉴于本文研究不同政府干预条件下产业集聚对能源效率的影响，参考Gowrisankaran et al（2015）模型的思想，首先将产业集聚纳入厂商短期生产函数：

其中：G和K分别表示产业集聚和资本投入，且二者正相关，即∂Q/∂K＞0；E表示厂商为提升能源效率所发生的投资，其与能源效率正相关。短期内，在厂商投资总额固定的前提下，其用于改善能源效率的投资和用于生产的投资必然互为消长。考虑到能源效率的提升对企业产出的增加具有一定的滞后效应。因此，短期内能源效率投资与产出呈负相关关系，即∂Q/∂E＜0；α表示弹性系数。

厂商获取资本用以购买机器设备，但同时需要支付利息。考虑到产业集聚正外部性中的共享效应，本文假设所有厂商共同承担支付给设备的报酬R=G-γ Kr。同时，机器设备的运行需要消耗能源为其提供动力，令动力成本C=E-β K。则考虑资本利息和动力成本后，厂商生产利润函数为

其中：r表示利率；γ表示产业集聚基础设施共享效应弹性，γ＞0；β表示能源效率投资的动力成本弹性，由于该指标存在不可逆约束。因此β＞1。

由公式（2）计算厂商利润最大化的一阶条件：

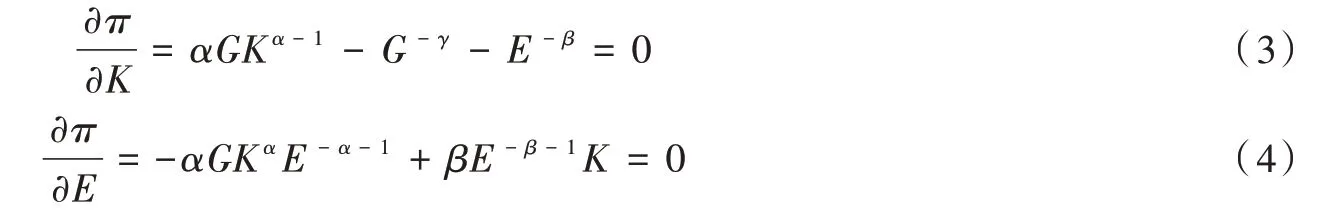
则均衡状态下最优资本存量为

最优能源效率投资为

进一步分析能源效率与产业集聚及利率的关系可知：

公式（7）显示，产业集聚与最优能源效率投资呈正相关关系，由于最优能源效率投资与能源效率也呈正相关关系，可以得到，产业集聚与能源效率同样呈正相关关系。

如前文所述，地方政府GD0 博弈竞争过程中，政策租是各级地方政府“引资大战”的重要工具，将政策租φ（G）纳入厂商利润函数：

经济发展水平直接影响市场规模，两者一般呈正相关关系，经济发展水平相对落后的地区往往不具备完善的市场结构和合理的市场规模，从而失去要素流动的吸引力，导致较低的产业集聚水平。这类地区的政府更倾向于使用政策租工具以吸引投资，拉动经济增长。从投资厂商的角度看，为了获得更多的政策租支持，可能会选择产业集聚水平较低的地区作为投资对象。因此，产业集聚可以作为内生变量处理。根据式（9）的分析结果，采用链式法可以推导出政策租对厂商能源效率投资的影响：

陈抗等（2002）研究发现，地方政府的干预行为可以解释为“援助之手”和“攫取之手”。从式（12）不难看出，地方政府用政策租工具干预经济带来的产业集聚并不能改善能源效率，相反，不合理的政策租工具更趋向于导致资源配置扭曲，最终抑制能源效率的改善。或者说，以短期利益为目标的政策租占据主导地位时，地方政府其更趋向于伸出“攫取之手”。

可见，在政治晋升博弈中，单纯基于政绩考虑提供政策租，往往带来的不是真正意义上的“产业集聚”，相反，其导致的资源扭曲配置效应抑制了产业集聚应有的绩效，无法改进能源效率。

基于此，本文提出假设1：

政府发展性支出在产业集聚影响能源效率过程中存在调节效应。

进一步分析，出于政绩考量的地方政府在政治晋升博弈中，更倾向于提供高额政策租以吸引企业投资，从而形成同质企业扎堆现象，难以实现产业集聚应该发挥的真实绩效，这种不合理的政策租最终使产业集聚产生扭曲效应。那么，为了发挥产业集聚应有的绩效，政策租数量应该控制在什么样的合理区间范围内呢？本文构建政府目标函数：

其中：W为政府目标；π表示辖区内企业利润水平；F表示财政收入；s表示国有企业所占比重；i表示预算外收入所占比重；u、v为大于零的参数。

鉴于地方政府需要同时考虑政绩和财政激励，对式（13）求偏导：

相对于民营企业，国有企业在就业、养老等方面更具优势。因此，地方政府政绩考量，更趋向于提高国有企业的占比。同时，地方政府为了降低其对显性收入的依赖，更倾向于增大预算外财政收入的占比。因此，对式（14）继续求二阶导数可得：

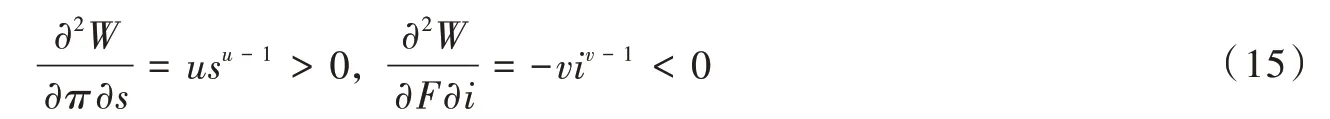
前文式（9）表明，企业利润与政策租呈正相关关系，企业为了获得正常利润以外的超额利润，更趋向于获得更多的政策租，假定：

企业要求的政策租越多，政府的财政盈余状况越趋于恶化：

加入政策租变量，政府目标函数可以改写为

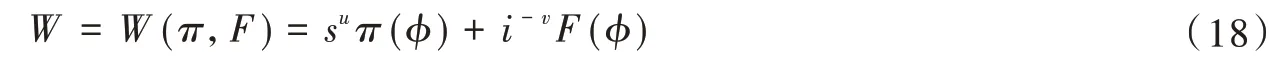
为了达到政绩和财政双重激励的均衡，地方政府可选择的政策租数量为

对式（19）求偏导可得：

式（20）表明，国有企业占比较高及预算外财政收入占比越高的地区，理论上伴随着更高的政策租。

进一步，将政府目标函数纳入式（12），求导可得：

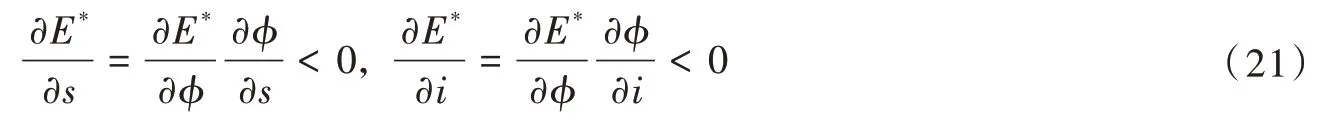
可见，国有企业和预算外收入占比均会对能源效率产生负面抑制作用。为了在政治晋升博弈中取胜，地方政府提供政策租的初期，受额外利润的诱导，不同类型的企业开始集聚，异质企业的集聚并不能发挥产业集聚应有的溢出效应，能源利用效率降低；随着政策租力度的加大，同质企业集聚数量增加，产业集聚的溢出效应显现，能源效率得到提升；然而，过多的政策租将引发地方政府的财政预算约束软化、资源配置扭曲，进而使能源效率恶化。可见，产业集聚对能源效率的影响伴随着政策租数量的不断增加，呈现先抑制、后促进、再抑制的作用路径。

鉴于此，本文提出假说2：

产业集聚影响能源效率的过程中伴随着政府发展性支出不断加强，呈现先抑制、后促进、再抑制的倒“N”型作用路径。

四、计量模型和数据说明

（一）基准回归模型

如前文所述，地方政府目标异化和边界模糊化可能对产业集聚产生正向或负向影响，进而作用于能源效率和经济增长。本文首先构建静态面板数据模型，分别从能源效率和能源强度两个角度验证政府发展性支出是否对产业集聚具有调节效应，为了减弱异方差对模型的影响，对所有变量去对数处理：

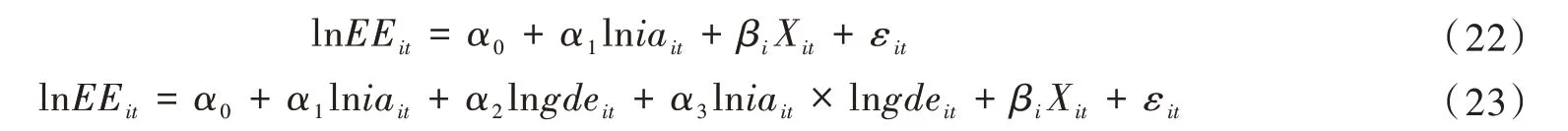
其中：i、t分别表示城市和年份；εit为随机扰动项；能源效率和产业集聚水平分别用EEit和iait表示；Xit表示一组控制变量。式（22）为基准回归模型，只分析产业集聚对能源效率的影响。为了验证政府发展性支出对产业集聚的调节效应，将模型（22）进行扩展，加入政府发展性支出与产业集聚的交互项。式（23）中，gdeit表示政府发展性支出；lniait ×lngdeit表示政府发展性支出与产业集聚的交互效应。

（二）面板门槛回归模型

如果政府发展性支出对产业集聚产生调节效应，促进或抑制产业集聚应有的外溢效应，进而作用于能源效率，那么，政府发展性支出的合理区间应该如何确定。为了回答这个问题，本文构建面板门槛回归模型，考察政府发展性支出对产业集聚不同调节效应的门槛值：

与式（22）、式（23）相比，式（24）中响应变量的含义有所变化。其中，d(*)为示性函数；gdei为门槛变量；α11和α12分别表示在q≤gdei和q＞gdei时产业集聚对能源效率的弹性系数。如果门槛选择合理，α11和α12的估计值或符号应显著不同。公式（24）仅分析了单门槛效应，考虑到多重门槛的分析过程与单门槛类似，不再赘述，在实证分析部分本文将进行多重门槛验证和分析。

（三）变量数据说明

1.被解释变量：绿色能源效率（EE）

本文借鉴史丹和李少林（2020）的研究成果，采用卫星夜间灯光指数，模拟测算各地级市能源消费量，并将资本（2004 年为基期）、劳动、能源作为投入变量，将GD0（2004 年为基期）作为期望产出，工业二氧化硫、工业烟粉尘和工业废水作为非期望产出，运用SBM-Malmquist-Luenberger 指数法测算得到各地级市绿色能源效率。具体计算过程如下：

鉴于本文测算的是地级市绿色能源效率，首先需要构建包含期望产出和非期望产出的生产可能性集。为了弥补传统DEA方法和SFA方法的不足，借鉴Oh和Heshmati（2010）的研究成果，采用序列DEA技术构造生产可能性集。假设决策单元k(k=1，2，…，K)在每个时期t(t=1，2，…，T)有I种投入要素x(x=1，2，…，I) ∈，M种期望产出y(y=1，2，…，m) ∈和N种非期望产出b(b=1，2，…，N) ∈，绿色能源效率的生产可能性集可表示为

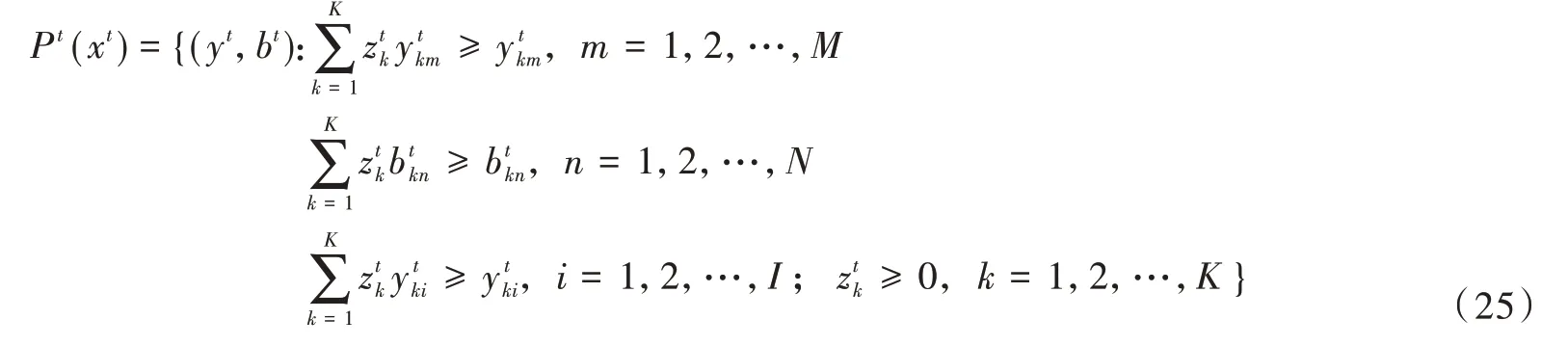
在公式（25）的基础上，基于产出导向的方向距离函数可表示为

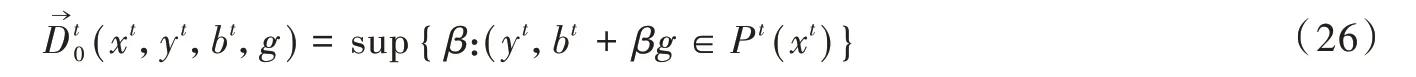
其中：g=(gy，gb)为产出扩张的方向向量，由于本文测算的是绿色能源效率。因此，希望增加期望产出，减少非期望产出。假定期望产出与非期望产出的增减比例相等，即g=(gy，-gb)。β为期望产出与非期望产出增减比例的最大可能值。

运用DEA 求解方向性距离函数相当于求解如下线性规划：

在式（27）的基础上，借鉴Oh和Heshmati（2010）的研究，构建基于产出导向的SML（sequential Malmquist-Luenberger）指数并将其分解为规模效率变化指数（SEC）、技术进步变化指数（TC）和纯技术效率变化指数（PEC）：

其中：SML指数表明了(xt+1，yt+1，bt+1；gt+1)相对于(xt，yt，bt；gt)生产率的变化，SML＞1 表示生产率水平提高了，反之，生产率水平降低了；TC表示不同时期相同投入的最优产出比，TC＞1 表示生产技术有进步，反之，生产技术衰退；EC表示相邻两期技术效率变化对绿色能源效率的贡献程度，EC＞1 表示能源效率有所改善，反之，能源效率下降。

2.核心解释变量：产业集聚（ia）

目前，针对产业集聚的研究较为丰富，产业集聚代理指标的选取也各有不同。鉴于制造业对能源效率的影响程度，本文借鉴王佳和陈浩（2016）的研究，选取制造业集聚作为产业集聚的代理指标，采用区位商计算得到：

其中：Iij表示i城市制造业的从业人员数；Ii表示i城市的总就业人数；Lj表示全国制造业从业人员数；L表示全国总就业人数。

3.门槛变量：政府发展性支出（gde）

鉴于中国地方政府在要素流通、地方基础设施供给和政策租提供等方面的重要作用，本文借鉴赵勇和魏后凯（2015）的研究，采用非公共财政支出比重作为政府发展性支出的代理指标：地方政府非公共财政支出比重=（地方政府财政支出-教育支出-科学支出-社会保障与就业支出）/地方政府财政支出。

4.其他控制变量

技术进步水平（tpit），技术水平的提升将带来生产设备的效率提高，节约生产过程中的能源消耗，进而直接作用于能源效率。同时，技术水平的提升有利于提高生产者的素质和节能意识，进而间接作用于能源效率，本文选取各地级市历年发明专利申请数作为技术进步水平的代理指标。产业结构（strit），鉴于第二产业对能源依赖性更强，本文选取第二产业增加值占GD0 的比重作为代理变量。工业结构（indstrit），以限额以上工业总产值占GD0 比重衡量。经济发展水平（pgdpit），以人均地区生产总值（2004 年为基期）衡量。人口密度（pdit），以各地级市人口数除以行政区面积衡量，表示各城市人口活动规模的差异影响。对外开放度（openit），本文选取地区进出口贸易总额与国内生产总值的比重作为对外开放度的代理指标。人力资本水平（hcit），理论上，受教育水平越高，节能减排的意识就越强，本文选取各地级市历年普通高校在校生人数和地区年末户籍人口数的比值作为人力资本水平的代理指标。

由于部分地级市新设或撤销及相关变量数据缺失，本文选取2004—2017 年中国268 个地级市作为研究对象。同时，鉴于本文主要分析中国内陆地区城市能源利用问题。因此，未考虑港澳台地区的城市。本文数据主要来自《中国统计年鉴》（2005—2018）、《中国城市统计年鉴》（2005—2018）、《中国能源统计年鉴》（2005—2018）、《中国环境统计年鉴》（2005—2018）具体指标、数据说明及统计性描述见表1。

表1 变量选取及数据来源

为了避免计量分析过程中变量内生性问题的干扰，本文在基准回归模型验证的基础上选取工具变量，采用两阶段最小二乘法（2SLS）来解决内生性问题对计量回归结果的偏误性影响。为了保证计量回归结果的稳健性和可信性，本文借鉴已有研究的基础上，选取制造业就业密度（edit）及其滞后一期L.edit作为工具变量，以检验基准计量模型中产业集聚是否存在内生性问题。其计算公式为

其中：i表示省份；t表示年份；Mit表示t年i省制造业的就业人数；Sit表示t年i省的土地面积。

五、实证结果及分析

（一）能源效率、产业集聚、政府干预的核密度分析

根据上文表1 中的指标说明，运用Stata 软件，根据Epanechikov 核函数选取最佳带宽，选取2004 年、2006年、2008 年、2010 年、2012 年、2014 年和2017 年绿色能源效率、产业集聚和政府发展性支出数据，描述三者的动态变化特征，如图1 所示。

图1 绿色能源效率、产业集聚、政府发展性支出的核密度分布

观察能源效率核密度分布图，从峰度上看，2004—2017 年，中国绿色能源效率分布均呈单波峰分布且高度逐渐下降，尤其在2006 年以后下降幅度非常显著，这说明中国各地区能源效率的差异性在不断缩小，各地区能源效率分布趋于收敛。从偏度上看，2008 年以前，绿色能源效率整体呈现左拖尾，说明低能源效率地区占比较大，2008 年以后，尤其是2017 年，能源效率核密度分布呈现显著的右拖尾，说明中高能源效率地区的占比明显增加。从绿色能源效率波峰对应的效率值看，样本期内，该值在持续右移，说明大部分地区能源效率值在持续上升。

同样，观察产业集聚的核密度分布图，从峰度上看，样本期内，各地区产业集聚的核密度分布呈现单峰分布且峰度变化不显著，说明不同地区产业集聚水平的差异较大。从偏度上看，2004—2014 年间，产业集聚核密度均呈左拖尾分布，说明这段时期，各地区低产业集聚地区占比较大。2014 年以后，产业集聚核密度均呈显著的右拖尾分布，说明2014 年以后，高产业集聚地区占比在显著增加。从核密度波峰对应的产业集聚数值可以看出，2004—2017 年间，中国各地区产业集聚核密度波峰对应的产业集聚值呈左右微小波动变化，说明整体产业集聚水平比较平稳。

与能源效率、产业集聚相比，政府发展性支出的核密度分布呈现了不同的特征。从峰度上看，样本期内，各地区政府发展性支出整体上呈现不严格的单峰或双峰分布，说明部分地区政政府发展性支出存在不合理状况。从偏度上看，2004—2017 年间，各地区政府发展性支出均呈现显著的右拖尾分布，说明大部分地区都处于高政府发展性支出状态。从核密度波峰对应的政府发展性支出数值可以看出，样本期内，该值在不断右移，说明大部分地区的政府发展性支出力度仍在持续上升。

综上所述，样本期内，能源效率与产业集聚呈现相似的分布特征。而与二者相比，政府发展性支出的分布特征差异较大。那么，政府发展性支出在产业集聚与能源效率提升过程中扮演什么样的角色？该问题在下文的计量分析中予以解答。

（二）基准回归结果及分析

为了解答上文提到的问题，本文构建静态面板数据模型，分析产业集聚和政府发展性支出对能源效率的作用机理。根据Hausman 检验结果分别采用固定效应模型和随机效应模型进行分步回归，得到模型1～模型5，分析结果见表2。

表2 基准估计结果及分析

模型1 中未加入政府发展性支出和其他控制变量，仅检验产业集聚对绿色能源效率的影响，结果显示，产业集聚对能源效率产生负向抑制作用且在1%的显著水平下通过检验。同理，模型2 显示，政府发展性支出对能源效率产生正向促进作用，但是未通过显著性检验。模型3 中加入政府发展性支出变量及二者的交互项，结果产业集聚对能源效率的影响系数从负号变为正号，但未通过显著性检验；政府发展性支出对能源效率的作用系数从正号变为负号，且在1%的显著水平下通过检验；政府发展性支出与产业集聚的交互项显著为正，且在1%的显著水平下通过检验。对模型1、模型2 进行扩展，加入其他控制变量，得到模型4。政府发展性支出与产业集聚的系数均显著为负，但是，相比模型1，产业集聚的系数从-0.0675下降为-0.0373，说明样本期内，政府发展性支出对产业集聚产生了正向的调节作用。为了验证该结论，对模型4 进行扩展，加入政府发展性支出与产业集聚的交互项，得到模型5。从计量结果不难发现，产业集聚对能源效率的影响系数方向发生变化，从-0.0373 变为0.0142。虽然政府发展性支出对能源效率的影响系数显著为负，但是交互项对能源效率的影响系数显著为正，达到0.0296 且在1%的显著水平下通过检验。这就验证了模型4 的结论，也验证了前文的理论假说1，政府发展性支出在产业集聚影响能源效率过程中产生调节作用。

综合看来，政府发展性支出在产业集聚影响能源效率的过程中产生了显著的调节效应，那么这种调节效应的作用程度和方向如何确定，即政府发展性支出的边界在哪里。为了回答该问题，本文将政府发展性支出作为产业集聚影响能源效率的门槛变量，构建面板门槛模型，分析不同政府发展性支出水平下，产业集聚对能源效率影响的异质性。

（三）内生性问题讨论

上述基准计量回归结果可以看出，政府发展性支出在产业集聚影响能源效率过程中存在调节效应，尽管这种调节效应在统计意义上具有显著性，但不具有稳定的显著性意义。仍然存在内生性问题干扰计量回归结果稳健性的可能。对此，本文采用工具变量法对基准回归结果进行计量检验。鉴于制造业与其他行业相比，对能源的消耗更大，对能源效率的影响更加敏感。因此本文采用制造业的就业密度（ed，制造业从业人数/面积）及其之后一期（L.ed）作为产业集聚的外生工具变量，采用两阶段最小二乘法（2SLS）对模型1、模型3～模型5 进行检验得到模型6～模型9，结果见表3。

用工具变量法进行两阶段最小二乘（2SLS）回归时，必须对外生工具变量的有效性进行检验。表3 汇报了工具变量的系列检验结果。首先，模型6～模型9 中，不可识别检验Anderson canon corr.LM 均在1%的显著水平上拒绝原假设，表明选取的外生工具变量与内生解释变量相关且可识别；其次，模型6～模型9 中，弱工具变量检验Cragg-Donald WaldFstatistic 的值分别为46.123、32.170、78.727、38.522，均显著大于10%显著水平下的临界值19.93，拒绝弱工具变量的原假设；再次，过度识别Sargan 检验结果显示，模型6～模型9 中，Anderson canon.corr.LM statisticP值分别为0.9149、0.9486、0.4440 和0.6146，均在1%的显著水平下接受原假设，所有工具变量均有效。并且，回归结果中，核心解释变量和各控制变量的系数大小、符号、显著性也与基准回归基本相符，故认为回归结果在统计上不存在内生性问题。

表3 工具变量回归结果

（四）政府发展性支出门槛估算

借鉴Hansen（1999）的研究成果，本文采用Stata14.0 软件进行实证研究，首先对变量门槛效应进行检验，结果见表4。

表4 显示，以政府发展性支出（gdeit）作为门槛变量，在5%的显著水平下通过了单一门槛和双重门槛检验，而三重门槛没有通过显著性检验。门槛效应自抽样检验之后，需要对双门槛模型的门槛值估计结果进行检验，如表5 和图2所示。

表4 门槛效应自抽样检验

图2 双门槛估计值和置信区间

表5 显示了两个门槛估计值和95%置信区间。借助图2 绘制的似然比函数图，可以更加直观、清晰的理解门槛值估计和置信区间的构造过程。门槛变量的估计值为似然比检验统计量LR为零时的取值，在本文的双重门槛模型中分别为0.2517 和0.2946。图2 中的虚线表示两个门槛值95%置信区间在所有LR 值小于5%显著水平下的临界值7.35。因此，可以根据两个门槛值将268 个地级市分为低政府发展性支出(gde≤0.2517)、中等政府发展性支出(70.2517 ＜gde≤0.2946)和高政府发展性支出(gde＞0.2946)三种类型，不同政府发展性支出类型中产业集聚对能源效率的影响见表6。

表5 门槛值估计结果

表6 的回归结果显示，产业集聚影响能源效率的过程中，存在政府发展性支出水平的双重门槛效应。从回归系数看，在不同的政府发展性支出水平下，产业集聚对能源效率的影响存在显著的差异性。具体的，在低政府发展性支出水平区间(gde≤0.2517)内，产业集聚对能源效率产生显著的抑制作用，其回归系数为-0.0371，且在1%的显著水平下通过检验；在中等政府发展性支出水平区间(0.2517 ＜gde≤0.2946)内，产业集聚对能源效率的影响系数从负数变为正数，其回归系数为0.0244，且在10%的显著水平下通过检验，说明产业集聚对能源效率产生正向促进作用；在高政府发展性支出水平区间(gde＞0.2946)内，产业集聚对能源效率的作用方向再次发生改变，其回归系数为-0.1416，且在1%的显著水平下通过检验，产业集聚再次对能源效率产生负向抑制作用。可见，以政府发展性支出作为门槛变量，产业集聚与能源效率存在显著的先抑制、后促进、再抑制的倒“N”型关系，这也验证了前文理论分析中的假说2。之所以产生这样的结果，是因为产业集聚可能促进地区能源效率的提升，但产业集聚质量受地方政府发展性支出的影响。具体分析如下：在低政府发展性支出水平下，经济主体在约束条件下追求目标最优化行为所形成的集聚是由市场化引发的，少量的政策租并不能吸引技术水平尤其是节能技术水平较高的企业形成集聚。技术水平相对较低的企业形成的表面集聚并不能发挥产业集聚应该发挥的技术外溢效应，能源效率并不能得到提升。在中等政府发展性支出水平下，经济主体的集聚是由市场化和政府共同引发的。对于经济主体而言，集聚的内涵在于能够借助外部性经济降低交易成本，使得平均成本整体下降。经济主体之间可以通过技术外溢和共享，提升能源利用技术，提高能源效率。同时，政府可以通过能源价格杠杆，刺激经济主体提升能源利用技术，推动能源要素不断从低效率部门向高效率部门流动。因此，在此过程中，政府发展性支出行为可以促进能源效率的提升。在高政府发展性支出水平下，地方政府为了在“GD0”竞赛中获胜，产生依靠政府发展性支出推动经济增长的动机。单纯以经济增长为目的的地方政府，更加关注投资辖区企业的规模和数量，忽略了企业之间的关联性及投资行为的合理性，进而推出大量只处于推动经济增长的“政策租”。为了追逐“政策租”，不具备关联性甚至是性质相悖的企业形成表面上的产业集聚（企业扎堆），这种表面的产业集聚难以对能源效率产生正向影响，甚至产生负面作用：一方面，政府发展性支出诱导下企业表面上的产业集聚导致低水平竞争过程中的过度投资、重复建设和资源浪费，由此引发的资源配置扭曲，无法发挥真正意义上产业集聚应有的技术溢出效应，相反，使能源利用效率更加恶化；另一方面，环境作为公共产品，具有非竞争性和非排他性。政府加大环境规制力度则会增加企业污染治理成本，然而单纯以经济增长为目标的政府，为了吸引企业投资，会降低对企业的环境规制力度，甚至对本地区高污、高排企业持纵容态度，从而损失了包含环境信息的能源利用效率。因此，在此过程中政府发展性支出行为抑制了能源效率的提升。

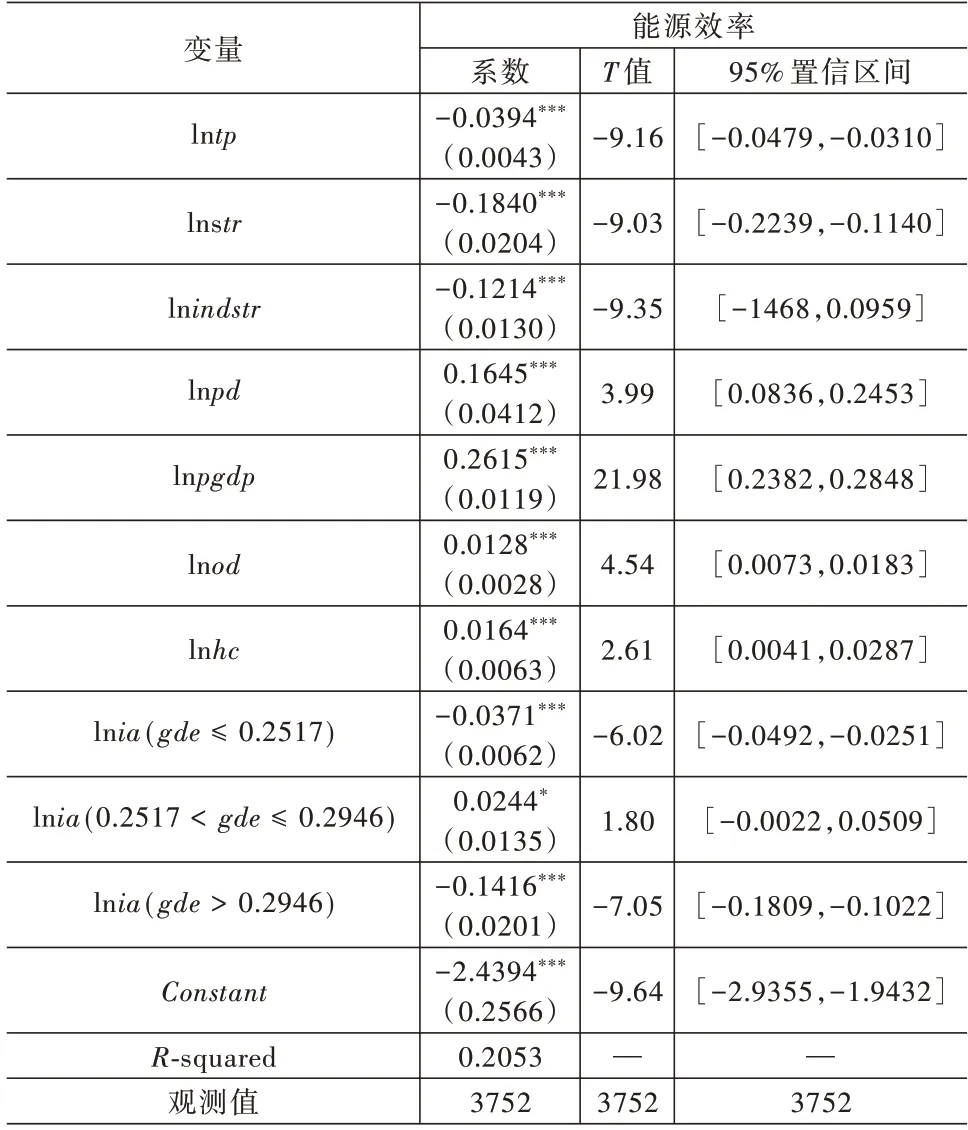
表6 政府发展性支出双重门槛参数估计结果

其他控制变量的回归结果与基准回归结果的系数基本一致，所有变量估计结果方向和显著性没有显著差异，只是具体数值发生微小变化。可见计算结果是稳健的，说明本文的实证结果具有可靠性。

六、结论和政策建议

为了探索政府发展性支出在产业集聚影响能源效率过程中的边界，本文以2004—2017 年中国268 个地级市为研究对象。首先，从理论上阐明政府发展性支出在产业集聚影响能源效率过程中存在调节效应，伴随着政府发展性支出的不断增加，产业集聚对能源效率的影响呈倒“N”型作用路径。表明过低或过高的政府发展性支出都不利于产业集聚正外部性作用的发挥，进而抑制能源效率的改善，只有适度的政府发展性支出才能发挥产业集聚应有的绩效，有助于能源效率的提升。其次，通过固定效应模型和工具变量法，验证了上述理论假说。最后，采用面板门槛模型研究发现，产业集聚影响能源效率的过程中存在政府干预的双重门槛效应，门槛值分别为0.2517 和0.2946，对政府发展性支出分组进行的计量回归结果，也验证产业集聚对能源效率的影响路径与倒“N”型相吻合。研究表明，过高或过低的政府发展性支出行为将抑制能源效率的提升，适度的政府发展性支出有利于改善能源效率。基于以上研究结论，本文提出如下政策启示：

第一，积极营造良性的产业竞争环境，实现真正意义上的产业集聚。产业集聚需要通过技术外部性来实现对能源效率影响的正外部性，而良性竞争的集聚环境是技术外部性得以实现的前提条件。市场竞争规范性缺失，将导致产业过度竞争，进而抑制产业集聚正外部性效应的发挥。所以，各级地方政府应该通过知识产权、专利等措施保护创新成果，引导产业良性竞争，营造良性的产业集聚环境。第二，硬化地方政府财政支出约束，明确地方政府的行为边界。地方政府建立公开透明的财政预算监管体系，进一步完善财政预算制度。将公共支出以外的财政支出逐渐纳入预算体系，规范其使用范围，矫正公共支出以外财政支出的使用目的。从根本上规范地方政府行为，引导其指定合理的长期发展规划。第三，遵循市场规律，减少地方政府利用“政策租”而对经济的直接干预。各级地方政府应有效控制针对外来企业的税收优惠和财政补贴，不断增加公共产品（科学研究、基础设施、人力资本培训等）供给，尤其对于企业研发投入的财政补贴。不断克服由于企业研发投入不足导致的技术溢出正外部性难以实现问题，诱发产业集聚的外溢和共享效应，实现能源效率的提升。