面向鲜食葡萄无损采运的果穗系统振碰复合动力学建模

2022-03-07刘继展阳开雨

江苏大学学报（自然科学版） 2022年2期

刘继展，阳开雨

(江苏大学农业工程学院，江苏镇江 212013)

我国葡萄生产在近40年得到了极大的发展，据统计，2017年我国葡萄总产量1 316.1万t，其中85%为鲜食葡萄，其产量和消耗量均占全球的1/2.生产中鲜食葡萄必须以成串的形式完成摘取、夹送、夹放、躺放和产后的分选、装箱、运输等采运全周期的作业.在此过程中，果穗因为振动、碰撞而掉落、腐烂的损失高达20%～30%,而果串完整性和果粒无损性是鲜食葡萄品质评价的两大指标[1].显然，落粒与伤粒问题已经成为了鲜食葡萄产运全过程中的瓶颈.

近年来，国内外学者对葡萄果实采运过程中因为振动和碰撞造成的落粒与伤粒的问题展开了一系列的研究.针对葡萄果穗的振动问题，文献[2]发现了葡萄果穗在夹持移送启停与加持部位不同的情况下，振动影响果粒脱落率的规律；文献[3]利用低频运输试验台进行试验发现，40 Hz振动频率对巨峰葡萄的损伤最大；文献[4]试验发现了5～10 Hz振动对包装鲜食葡萄果穗的落粒率影响最大；文献[5]将果梗离散为5 mm小圆柱并以Bush连接实现柔性化、果粒与果柄之间采用弹簧阻尼模型建立了三维葡萄果穗模型.针对葡萄果穗系统中果粒碰撞的问题，文献[6]通过试验发现葡萄果粒的跌落冲击对生理品质有显著影响；文献[7]利用电子果实对机械采收和运输过程中葡萄果粒的碰撞进行了研究.但是，对葡萄果穗内果粒碰撞，以及对其振碰复合模型的研究较少.

为探明鲜食葡萄产运全过程中果穗振动与果粒碰撞的内在规律，文中开展葡萄果穗振碰复合动力学模型的研究，揭示产运过程中振碰导致的脱粒和伤粒规律，为实现高效低损的鲜食葡萄作业提供参考.

1 激励异质性与振碰复合性

在采运全周期，鲜食葡萄经受摘取、夹送、躺放、运输时，分别从主穗轴，底部输入夹剪偏差激励、启停激励、冲击激励、周期激励，如图1所示，并引起果穗具有明显分布差异的自由振动、强迫振动和并发的果粒碰撞.果穗的振碰对果穗的落粒和果粒的伤粒有促进作用，所以探明果穗振碰规律对于解决落粒、伤粒问题有重要的意义.

图1 鲜食葡萄采运全周期的多级异质激励

2 模型基本假设与结构说明

2.1 基本假设

葡萄果穗振碰复合动力学模型的基本假设如下：① 假设果粒碰撞时不考虑果粒与果粒之间的摩擦效应；② 假设主穗轴、果粒材质分别具有各项同性，忽视果皮、果肉材质不同的影响；③ 假设只有果粒之间发生碰撞；④ 假设果梗和支梗均可由单个刚体圆柱或多个圆柱组成的刚体表示.

2.2 结构说明

葡萄果穗系统属于典型的带约束碰撞的非线性黏弹性体多体系统.为此，采用刚柔耦合建模的思路，在文献[8]提出的方法上进一步改进，提出了“柔性杆—铰链—刚性杆—柔性球”的方法，如图2所示.即主穗轴为柔性杆，支梗与果梗为刚性杆，果粒是柔性球，主穗轴与支梗之间以及支梗与果梗之间连接由黏弹性铰链定义，果梗与果粒之间固定连接.

图2 葡萄果穗振碰复合模型

3 葡萄果穗系统振动动力学模型

3.1 主穗轴和果粒的动力学方程

文中建立的葡萄果穗振碰模型中的主穗轴和果粒是柔性体，与目前商用多体动力学软件相似，都是采用的绝对节点坐标法对柔性体进行处理，能够有效地处理葡萄果穗系统在多源异质激励情况下的振碰复合仿真.采用绝对节点坐标法对柔性体划分三维实体单元.三维实体单元常采用的标准形式有梁单元、四面体单元、五面体单元等.由于农作物形状不规则的性质，文中采用比较简单的四面体单元来说明.从主穗轴和果粒中选取一颗果粒作为研究对象，由于柔性果粒离散的四面体单元过多，文中选取果粒上一点P所在的实体单元来进行说明，如图3所示.

图3 果粒四面体单元

在图3b中全局坐标系下，单元的节点坐标可表示为

exy=[(exy1)T(exy2)T… (exyn)T]T，

(1)

式中：exyn为第n个单元节点坐标.

带果梗约束的果粒在外部激励下做振碰运动的过程中，实体单元会发生变形，变形会引起单元内任意一点P的移动，所以对于移动的描述，单元内点P的绝对坐标r可由单元节点e来表示：

rxy=Nxyexy，

(2)

式中：Nxy为四面体单元的形函数，不同的实体单元具有不同的形函数.

根据式(2)，葡萄果粒实体单元的动能为

(3)

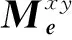
根据连续介质力学理论，果粒实体单元的势能为

(4)

式中：εxy为Green应变张量；σxy为第二Piola-kirchhoff应力张量.

果粒实体单元的Green应变张量εxy以位移的线性和非线性部分来表示：

(5)

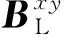
由式(5)，可得到虚应变为

(6)

由虚功原理，结合式(6)，可推出：

(7)

将式(5)代入式(7)，可以得到单元的弹性力为

(8)

由虚功原理，可得到柔性体果粒单元的动力学方程：

(9)

即

(10)

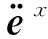
3.2 支梗和果梗的动力学方程

传统的多体系统动力学软件使用的绝对节点坐标法对于刚柔耦合的多体系统的刚性物体也要划分单元，这样导致纯粹的绝对节点坐标法较难处理葡萄果穗系统支梗果梗这种刚体比较多的模型.文中建立的葡萄果穗振碰复合模型中，支梗和果梗都是刚体，都是由不同尺寸的圆柱刚体或多个圆柱刚体组合而成的，如图4所示.

图4 支梗和果梗示意图

对刚体使用两基点的绝对坐标矢量描述刚体的位置和方向：

(11)

式中：dz为包含基点A和B的圆柱体的非独立坐标矢量(见图5).

图5 两基点圆柱刚体

A和B两基点具有刚体距离约束：

(12)

由式(11)、(12)，可得到刚体的动力学方程：

(13)

3.3 果穗系统振动动力学方程

由式(10)、(13)，可得葡萄果穗系统的振动动力学方程：

(14)

式中：C为刚体与柔体之间的约束方程；Cp为刚体与柔性体对广义坐标p的Jacobi矩阵.

4 葡萄果穗系统振碰复合动力学模型

4.1 果粒实体单元应力的计算

在果穗振碰复合模型中，果粒均为柔性实体，而且农作物普遍具有黏弹性的特点.假设果粒材料各向同性，所以根据文献[10]，可知三维分数阶导数黏弹性本构方程为

(15)

式中：h、d分别代表应力或应变的球量和偏量；G0为剪切松弛模量；G∞为初始弹性剪切模量；K0为体积松弛模量；K∞为初始体积模量.

依据分数阶导数算子的定义以及由Green应变张量E表示的应变矢量与第二Piola-kirchhoff应力张量S表示的应力矢量，代入式(15)，可得到黏弹性体的应力表达式[11]：

(16)

式中：Ni=τ0(h)-αAi；(D0D1D2)∈R6×6；[D0]=3K0Th+2G0Td；[D1]=3K∞Th+2G∞Td，[D2]为单位矩阵；

由式(16)可知：t时刻葡萄果粒的应力σ与该时刻的应变ε和t时刻之前的应力和应变都相关，这充分体现了黏弹性材料的遗传性质.同时，根据分数阶导数算子的离散过程可知，显然Nj>Nj+1，表明t时刻葡萄果粒的应力与t附近时刻的应力、应变关系远远大于非t附近时刻的应力、应变，这充分体现了黏弹性材料的衰退记忆性质.

4.2 碰撞检测

文中研究的碰撞问题主要是针对果粒之间的碰撞，所以假设碰撞只发生在葡萄果粒之间，忽视主穗轴、支梗、果梗之间的碰撞.因为要完成果粒碰撞阶段的仿真计算，所以判断果粒是否发生碰撞成为了关键点.碰撞示意图如图6所示，M、N两颗果粒发生相对运动时，如果碰撞发生，会产生碰撞接触点，没有发生碰撞则没有碰撞点.图中:

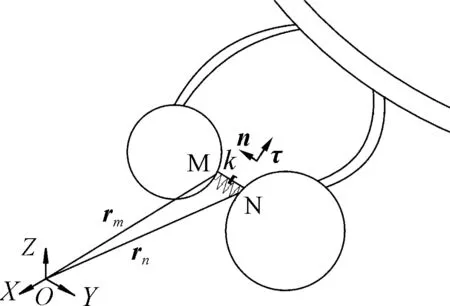
图6 葡萄果粒碰撞示意图

n为接触面单位法向量；τ为接触面单位切向量；K为等效弹簧弹性模量.

可能发生碰撞的点的碰撞侵入深度：

v=nT(rn-rm)，

(17)

检测可能发生碰撞的点是否发生了碰撞，发生碰撞的判据式：

v<0.

(18)

4.3 碰撞力计算

确定果粒发生碰撞后，进行接触力的计算.因为葡萄表皮一般来说比较光滑，所以假设忽略摩擦的影响.根据Hertz接触理论可知，此时接触力的数值大小就等于碰撞力的数值.果粒是黏弹性材料，因此葡萄果穗振碰耦合模型采用Kelvin模型来求解图6中所示的M和N两颗果粒之间碰撞力的大小.Kelvin模型是由开尔文元件一个理想弹簧和一个理想勃壶并联而成的[12]，碰撞力可根据Kelvin模型算出：

(19)

根据虚功原理，作用在果粒上任一点处的碰撞力可转化为单元广义力：

(20)

4.4 动力学方程求解

由式(14)、(16)、(19)、(20)，可得鲜食葡萄果穗系统振碰复合的动力学方程：

(21)

式中：Mx为柔性系统的质量矩阵；Mz为刚体系统的质量矩阵；q为柔性系统的广义坐标列阵；d为刚性系统的广义坐标列阵；λ为拉格朗日乘子列阵；C(qx,dz,t)为系统的约束方程；p=[qxTdzT]；Cp为约束方程对p的偏导数矩阵；Q为系统的广义外力；Fx为柔性系统当前时刻的弹力；σ为黏弹性体的应力.

(22)

式中：αi为BDF中的积分系数；k为积分阶数,具体形式可以参考文献[13].

通过积分方法可以得到式(21)的非线性方程组，然后采用牛顿迭代法在迭代过程中求解方程式和C(qx,dz,t)=0的Jacobi矩阵.至此，非线性方程组得以求解.

由式(21)可知，质量矩阵Mx、Mz为常数矩阵，该式中不存在非线性科式力和离心力项[14]，不仅可以避免坐标系转换的麻烦，还可以得到果穗系统振碰动力学方程.通过代入数值计算，便能得到果穗系统状态变量对时间的微商为核心项的描述状态变量随时间变化的等式[15]，从而达到从数值上描述果穗系统力与运动之间关系的目的.因为支梗果梗采用的自然坐标法来描述，所以建立的动力学方程在一定程度上相比传统的动力学软件仿真能减少计算量，提高仿真计算效率，对于葡萄果穗这样特殊的刚体、柔性体过多的系统能够达到较快仿真运算速度的效果.