平面应变条件下基于Lade-Duncan强度准则中主应力条件的土压力及其适用性

孟天一 张玉 刘瑾 赵阳 杨倩 丁潇 范特佳

摘 要：针对实际工程中大量存在的挡土墙、基坑开挖等平面应变问题，考虑中主应力对强度的影响，将平面应变条件下Lade-Duncan强度准则的中主应力关系代入SMP、Lade-Duncan、AC-SMP和广义Mises强度准则中得到新的平面应变强度准则。据此建立基于各强度准则的主、被动土压力计算公式，进而推广至黏性土，并将主、被动土压力理论计算值与实测值进行对比分析。结果表明，Mohr-Coulomb强度准则因其未考虑中主应力的影响，致使计算结果相比实测情况偏保守;SMP强度准则、Lade-Duncan强度准则考虑到中主应力对土压力大小的影响，计算结果相比Mohr-Coulomb强度准则更接近实测情况;AC-SMP强度准则、广义Mises强度准则在一定内摩擦角范围内可以描述挡土墙的土压力大小，但超出适用范围时，二者均不再适用于描述挡土墙的土压力大小;广义Mises强度准则在适用范围内的计算结果相比SMP强度准则、Lade-Duncan强度准则更接近实测数据。

关键词：平面应变;强度准则;中主应力;土压力

中图分类号：TU432   文献标志码：A   文章编号：2096-6717（2022）01-0020-08

收稿日期：2020-06-19

基金项目：国家自然科学基金（11802218）;陕西省科技计划（2019JQ-432）;陕西省黄土力学与工程重点实验室项目（LME201801）;陕西省教育厅专项科研计划（19JK0399、20JK0670）

作者简介：孟天一（1997- ），男，主要从事黄土力学研究，E-mail：312570571@qq.com。

张玉（通信作者），男，博士，副教授，E-mail：153673438@qq.com。

Abstract： In the engineering practice， the retaining wall and foundation pit could be regarded as a plane strain condition. Considering the influence of intermediate principal stess on the strength， we obtained the new plane strain strength criterions by substituting the intermediate principal stress relationship of Lade-Duncan strength criterion into SMP and Lade-Duncan， AC-SMP and the generalized Mises strength criterion. Based on these modified strength criterions， active and passive earth pressure models were established， and then extended to cohesive soil. The theoretical and measured values were compared and analyzed. The results show that the effect of intermediate principal stress on earth pressure is significant. The Mohr-Coulomb strength criterion fails to consider the influence of intermediate principal stress， and therefore the calculation results are more conservative than measurement. Considering the influence of the principal stress， the results of SMP and Lade-Duncan strength criterion are much closer to measurement than MC. The AC-SMP and generalized Mises strength criterion can describe the earth pressure of the retaining wall only within a certain range of friction angle， but when it exceeds the applicable range， both are no longer suitable. The calculations of the generalized Mises strength criterion， within the applicable range， are closer to actual data compared with the SMP and Lade-Duncan strength criterion.

Keywords：plane strain; strength criterion; principal stress in Lade-Duncan; earth pressure

擋土墙、基坑开挖等问题常可简化为平面应变问题，在平面应变条件下，中主应力对土压力有显著影响。Rankine土压力理论是基于Mohr-Coulomb 强度准则提出的，二者沿用至今，但均未考虑中主应力对土体本身强度的影响，与实测结果相比，计算出的主动土压力偏大，被动土压力偏小，这已被众多试验结果证实[1]。学者们通过不断的试验和研究已取得一定成果[2-4]：通过广义虎克定律计算出了中主应力表达式，结合双剪统一强度理论主应力型表达式推导出了Rankine主、被动土压力计算式;在平面应变条件下，结合Lade-Duncan强度准则和等效内摩擦角求解出了土体的主动土压力，提出了计算土压力的新公式;基于SMP强度准则中主应力条件，计算出了各强度准则下的主、被动土压力。SMP强度准则、Lade-Duncan强度准则、AC-SMP强度准则、广义Mises强度准则等考虑到中主应力对土强度的贡献[5-8]，在描述同一土体强度时，各种强度准则均能在其各自的适用范围内有效描述土的强度大小，但选取的中主应力表达式不同，计算结果与实测数据存在一定差异[9]。根据以上研究发现，SMP强度准则适用于无黏性土，Lade-Duncan强度准则是根据砂土真三轴试验成果的曲线拟合得到的，AC-SMP强度准则和广义Mises强度准则更适用于黄土[10]。Lade-Duncan强度准则中主应力条件与实际情况最为相符，笔者依据Lade-Duncan强度准则下的中主应力条件推导了几种平面应变强度准则，提出了无黏性土和黏性土平面应力状态下的主、被动土压力计算公式，并将其与实测数据进行对比分析，验证了基于各个平面应变强度准则所推导的主、被动土压力计算公式的适用范围及准确性。

1 土的常用強度准则

土的强度准则实质上反映的是土单元在破坏时的应力条件与土性参数之间所满足的关系。目前，针对土建立的强度准则包括Mohr-Coulomb准则、SMP准则、Lade-Duncan准则、广义Mises准则、轴对称压缩空间滑动面（AC-SMP）准则[11]。

1）Mohr-Coulomb强度准则

3 基于各强度准则的无黏性土主、被动土压力系数分析

3.1 主动土压力系数分析

依据将Lade-Duncan强度准则下的中主应力代入不同强度准则得到的大、小主应力关系，可以得出基于各强度准则的主动土压力系数Ka。整理各强度准则得到的主动土压力系数Ka随内摩擦角φ的变化规律，如图1所示。

由图1可以看出，依据平面应变条件下各强度准则得到的主动土压力系数随着内摩擦角的增大呈非线性减小趋势，主动土压力系数从小到大依次为AC-SMP强度准则、广义Mises强度准则、Lade-Duncan 强度准则、 SMP强度准则、Mohr-Coulomb 强度准则，基于各强度准则得到的主动土压力系数均小于 Mohr-Coulomb强度准则计算得到的主动土压力系数。当φ>40°时，广义Mises强度准则所计算出的主动土压力系数趋近于0，且随着内摩擦角的增大，主动土压力系数会有小于0的情况出现，此时该强度准则不适用于计算土压力。当0<φ<20°时，AC-SMP强度准则能够有效描述土压力大小。当φ>20°时，AC-SMP强度准则所计算出的主动土压力系数变化速率较大，且随着内摩擦角的增大，主动土压力系数会有趋于0的情况出现，此时该强度准则不适用于计算土压力。由此可以看出，各强度准则在考虑了中主应力影响的条件下计算出的主动土压力系数均小于Mohr-Coulomb强度准则。这表明Mohr-Coulomb强度准则在应用中趋于保守，未完全发挥出土体自身的强度特性。其余准则在其各自的适用范围内更趋近于实际情况，土体自身强度得到了有效的发挥。

3.2 被动土压力系数分析

与主动土压力系数计算方法相同，可得出基于各强度准则的被动土压力系数Kp。整理各强度准则得到的被动土压力系数Kp随内摩擦角φ的变化规律，如图2所示。

由图2可以看出，依据平面应变条件下各强度准则得到的被动土压力系数随着内摩擦角的增大呈非线性增大趋势，基于各强度准则得到的被动土压力系数均大于Mohr-Coulomb强度准则计算的被动土压力系数，被动土压力系数从小到大依次为Mohr-Coulomb 强度准则、SMP强度准则、Lade-Duncan强度准则、广义Mises强度准则、AC-SMP强度准则。当φ>30°时，广义Mises强度准则所计算出的被动土压力系数随着内摩擦角的增大而快速增大，

此时该强度准则不适用于计算土压力。当0<φ<20°时，AC-SMP强度准则能够有效描述土压力大小。当φ>20°时，AC-SMP强度准则所计算出的被动土压力系数随着内摩擦角的增大而快速增大，显然，AC-SMP强度准则在φ>20°时不适用于计算土压力。其余各强度准则的被动土压力系数计算结果增长速度均较为平缓，且未出现明显偏差，能较好地反映出被动土压力。

根据主、被动土压力系数与内摩擦角的关系可以看出，Mohr-Coulomb强度准则、SMP强度准则、Lade-Duncan强度准则均能较好地描述挡土结构上土压力的大小;当φ>30°时，广义Mises准则所计算的主、被动土压力系数已出现较大偏差，不再适用于文中条件下的土压力计算;当φ>20°时，AC-SMP强度准则所计算出的主动土压力系数已出现较大偏差，且被动土压力系数随着内摩擦角变化的斜率发生转折，显然已偏离实际情况，不再能准确反映该条件下的土压力。

4 平面应变条件下基于各强度准则的黏性土主动与被动土压力

基于以上各强度准则得到的无黏性土的平面应变主、被动土压力公式，其主应力状态经式（21）的变换，即可将不同平面应变土压力从无黏性土推广至黏性土，建立黏性土的土压力计算公式。

5 平面应变土压力理论算例与分析

5.1 无黏性土土压力验证

试验采用无黏性的松散砂土[15]，内摩擦角φ=34°，容重γ=19.56 kN/m3。挡墙由杂木板制成，厚5 cm、高1 m、宽1 m，并用两肋加强，以满足刚度要求。图3给出了试验时测得的主动土压力值，其中，h为墙高，Pa为墙体水平土压力。将砂土土性参数带入基于各个强度准则得到的主动土压力表达式，即可计算出各强度准则条件下挡墙不同深度处的主动土压力值，其与实测土压力曲线的比较如图3所示。

从图3可以看出，依据平面应变条件下各强度准则计算的主动土压力值随着深度的增加均线性增大，主动土压力计算结果从小到大依次为广义Mises强度准则、Lade-Duncan强度准则、SMP强度准则、Mohr-Coulomb强度准则，规律明显。

实测主动土压力值远小于基于Mohr-Coulomb强度准则的计算值，说明Mohr-Coulomb强度准则的计算结果过于保守，不利于提高工程经济性。开挖深度越深，基于各强度准则的主动土压力值差异越大，当开挖深度小于0.5 m时，Lade-Duncan强度准则、SMP强度准则的计算结果与实测值较为吻合;随着开挖深度继续增大，SMP强度准则的计算结果和实测值较为接近。基于广义Mises强度准则的计算结果在整体上和实测值最为接近;基于Mohr-Coulomb强度准则计算的主动土压力值最大，在应用于设计时过于保守，未能充分发挥土的自身强度;基于Lade-Duncan强度准则、SMP强度准则、广义Mises强度准则得到的主动土压力均体现了平面应变条件下中主应力对土强度的贡献，能较好地反映挡墙上的应力状态，与实测土压力值更为接近，其中基于广义Mises强度准则得到的主动土压力与实测土压力值最为接近。

5.2 黏性土土壓力验证

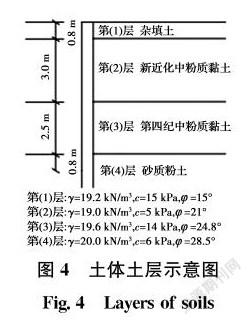
某基坑深7.1 m，采用桩径为800 mm的悬臂桩支护，桩长12.70 m。坑深内土层分布及各土层的土性指标见图4[16]。

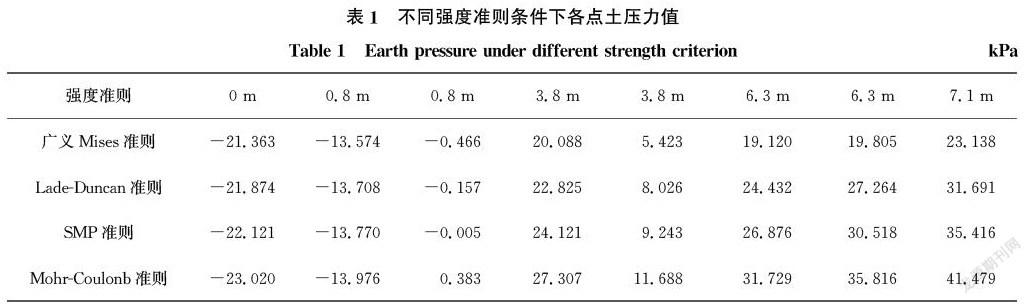
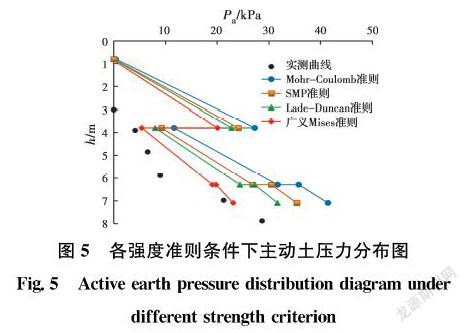
依据黏性土的主动土压力计算公式和各个土层的土性参数，可计算出基于各强度准则的不同土层深度处的主动土压力，将其整理后列于表1，沿基坑各土层上、下界面的土压力变化曲线见图5。

由表1和图5可知，基于广义Mises强度准则 计算出的主动土压力值与实测结果最为接近，基于Lade-Duncan强度准则、SMP强度准则计算的主动土压力值在整体上与实测结果较为接近，并均小于基于Mohr-Coulomb强度准则计算的主动土压力值。以3.8 m处不同强度准则条件下土压力计算值与实测值为例，如表2所示，广义Mises强度准则土压力计算值与实测值的比值为1.306、Lade-Duncan强度准则土压力计算值与实测值的比值为1.933、SMP强度准则土压力计算值与实测值的比值为2.241、Mohr-Coulomb强度准则土压力计算值与实测值的比值为2.815。计算结果表明，广义Mises强度准则、Lade-Duncan强度准则、SMP强度准则均能表现出中主应力对土体强度的影响，其中，广义Mises强度准则更能体现中主应力对土强度的贡献。

6 结论

1）在平面应变条件下，依据Lade-Duncan强度准则中主应力条件，得到基于不同强度准则下大、小主应力关系，推导出不同强度准则下主、被动土压力计算公式，并推广至黏性土。

2）各强度准则均有其适用范围，Mohr-Coulomb强度准则、SMP强度准则、Lade-Duncan强度准则在不同的内摩擦角条件下均能很好地描述挡土结构主、被动土压力;广义Mises强度准则适用于内摩擦角小于30°时的土压力计算;AC-SMP准则适用于内摩擦角小于20°时的土压力计算。

3）Mohr-Coulomb强度准则计算时未考虑中主应力的影响，导致计算结果偏于保守;基于广义Mises强度准则计算的主、被动土压力值与实测值最为接近。在考虑中主应力的条件下，各强度准则在其各自的适用范围内均能有效地描述土的主、被动土压力。

4）针对实际情况，在确保安全的前提下，选择合适的强度准则进行土压力计算，可充分发挥土的强度，达到节约成本、提高经济效益的目的。参考文献：

[1] 顾慰慈. 挡土墙土压力计算手册[M]. 北京： 中国建材工业出版社， 2005.

GU W C. Calculation of earth pressure on retaining wall [M]. Beijing： China Building Material Industry Publishing House， 2005. （in Chinese）

[2] 李广信. 实用主义与土力学[J]. 岩土工程学报， 2018， 40（10）： 1897-1904.

LI G X. Pragmatism and soil mechanics [J]. Chinese Journal of Geotechnical Engineering， 2018， 40（10）： 1897-1904. （in Chinese）

[3] 路德春， 梁靖宇， 王国盛， 等. 横观各向同性土的三维强度准则[J]. 岩土工程学报， 2018， 40（1）： 54-63.

LU D C， LIANG J Y， WANG G S， et al. Three-dimensional strength criterion for transverse isotropic geomaterials [J]. Chinese Journal of Geotechnical Engineering， 2018， 40（1）： 54-63.（in Chinese）

[4]  LI Z W， YANG X L. Active earth pressure for retaining structures in cohesive backfills with tensile strength cut-off [J]. Computers and Geotechnics， 2019， 110： 242-250.

[5]  SATAKE M. Stress-deformation and strength characteristics of soil under three different principal stresses [J]. Proceedings of Japan Society of Civil Engineers， 1976， 23（2）： 59-70.

[6] 罗汀， 姚仰平， 松冈元. 基于SMP准则的土的平面应变强度公式[J]. 岩土力学， 2000， 21（4）： 390-393.

LUO T， YAO Y P， SONG G Y. Soil strength equation in plane strain based on SMP [J]. Rock and Soil Mechanics， 2000， 21（4）： 390-393.（in Chinese）

[7]  WOODWARD P K. Earth pressure coefficients based on the Lade-Duncan failure criterion [J]. Engineering Structures， 1997， 19（9）： 733-737.

[8]  READES D W， DANIEL A W， GOLDSCHEIDER M. Cubical triaxial tests on cohesionless soil. Discussions of paper by P.V. Lade and J.M. Duncan， J. Soil Mech. Found. Div. Oct. 1973： 1F， 10R. J. Geothech. Engng. Div. V100， GT9， Sept. 1974， P1065-1069 [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts，1974， 11（12）： 241.

[9] 张玉， 邵生俊， 赵敏， 等. 平面应变条件下土的强度准则在黄土工程问题中的应用研究[J]. 土木工程学报， 2018， 51（8）： 71-80.

ZHANG Y， SHAO S J， ZHAO M， et al. Application research of soil strength criterion under plane-strain condition for loess problems [J]. China Civil Engineering Journal， 2018， 51（8）： 71-80. （in Chinese）

[10] 张玉， 邵生俊， 王丽琴， 等. 平面应变条件下土的强度准则分析及验证[J]. 岩土力学， 2015， 36（9）： 2501-2509.

ZHANG Y， SHAO S J， WANG L Q， et al. Analysis and verification of soil strength criteria in plane strain state [J]. Rock and Soil Mechanics， 2015， 36（9）： 2501-2509. （in Chinese）

[11] 陈昌禄， 邵生俊， 罗爱忠， 等. 土的静态空间滑动面及其强度准则适应性研究[J]. 地下空间与工程学报， 2015， 11（5）： 1185-1192.

CHEN C L， SHAO S J， LUO A Z， et al. Study on the static spatially mobilized plane and its strength criterion adaptability [J]. Chinese Journal of Underground Space and Engineering， 2015， 11（5）： 1185-1192. （in Chinese）

[12] 邵生俊， 張玉， 陈昌禄， 等. 土的3σ空间滑动面强度准则及其与传统准则的比较研究[J]. 岩土工程学报， 2015， 37（4）： 577-585.

SHAO S J， ZHANG Y， CHEN C L， et al. Strength criterion based on 3σ spatially mobilized plane of soils and its comparison with conventional criteria [J]. Chinese Journal of Geotechnical Engineering， 2015， 37（4）： 577-585. （in Chinese）

[13] 王骑虎. 岩土材料破坏准则基本特性分析[J]. 中国矿业， 2015， 24（12）： 142-146.

WANG Q H. Study on the basic characters of failure criterions of geotechnical material [J]. China Mining Magazine， 2015， 24（12）： 142-146. （in Chinese）

[14] 郑剑岳， 朱建明， 祝恩阳. 基于SMP准则的土压平衡盾构刀盘扭矩计算研究[J]. 地下空间与工程学报， 2017， 13（4）： 995-1000.

ZHENG J Y， ZHU J M， ZHU E Y. Torque calculation method of shield cutterhead in earth pressure balance based on SMP failure criterion [J]. Chinese Journal of Underground Space and Engineering， 2017， 13（4）： 995-1000.（in Chinese）

[15] 周应英， 任美龙. 刚性挡土墙主动土压力的试验研究[J]. 岩土工程学报， 1990， 12（2）： 19-26.

ZHOU Y Y， REN M L. An experimental study on active earth pressure behind rigid retaining wall [J]. Chinese Journal of Geotechnical Engineering， 1990， 12（2）： 19-26. （in Chinese）

[16] 谢群丹， 何杰， 刘杰， 等. 双剪统一强度理论在土压力计算中的应用[J]. 岩土工程学报， 2003， 25（3）： 343-345.

XIE Q D， HE J， LIU J， et al. Unified twin shear strength theory for calculation of earth pressure [J]. Chinese Journal of Geotechnical Engineering， 2003， 25（3）： 343-345.（in Chinese）

（编辑 黄廷）