基于改进的Legendre小波方法的期权定价

李钰 吕会影

(安徽机电职业技术学院 公共基础教学部，安徽芜湖 241000)

股票期权定价是金融衍生工具中的重要问题之一，在金融市场中广泛而成功地应用于风险对冲。因此，交易者可以通过使用期权调整交易策略和投资组合[1-3]。看跌期权是一种合同，给予持有者以行权价格E出售部分标的资产的权利(而非义务)。同样，给予持有者购买部分标的资产的权利(而非义务)是看涨期权。欧式期权和美式期权是两种常见的期权合约类型。欧式期权只能在到期日t=T执行，而美式期权可以在日期t≤T执行。

Black和Scholes(1973)提出了一个评估欧式期权的模型[4]，该模型至今仍被广泛应用于金融市场。该模型是在期权必须是无风险利率、标的资产的波动性已知且为常数、标的资产的收益遵循几何布朗运动等假设条件下建立的。在Black Scholes模型中，得到了欧式期权值V(S,t)作为以下偏微分方程(PDE)的解：

(1)

其中S为t时刻的股价，r为无风险利率，σ为标的资产的波动性。这个PDE给出了t时刻的看涨期权和看跌期权的价值，但Black-Scholes PDE很少可以有解析解的情况，如欧式期权情况。在欧式看涨期权中，支付函数是V(S,T)=max(S-E,0)，V(S,T)=max(E-S,0)是欧式看跌期权的支付函数。Black和Scholes(1973)给出了欧式看涨期权的解析解：

V(S,t)=SN(d1)-Ee-r(T-t)N(d2)，

(2)

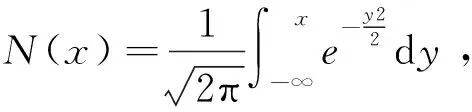
给出了欧式看跌期权的解析解：

V(S,t)=Ee-r(T-t)N(-d2)-SN(-d1).

(3)

然而，经过数次变量变换后，Black-Scholes PDE(1)变成了扩散方程，Wilmott 等人(1995)提出了另一种计算Black-Scholes PDE解析解的格式[5]。此外，通过使用Millen变换[6]，推导了求解Black-Scholes偏微分方程的直接方法。另一种推导Black-Scholes公式的方法是使用风险中性估值论证[3]。

正交函数族如正弦-余弦函数、块脉冲函数、勒让德(Legendre)多项式、切比雪夫(Chebyshev )多项式和卢盖尔(Luguerre)多项式被广泛应用于动态系统的近似解。使用正交基的主要优点是这个问题简化为求解代数方程组的问题。这可以通过截断正交基函数的级数来解决潜在问题，并使用算子矩阵来完成。如果我们用某些奇异的Sturm-Lioville问题(如Legendre或Chebyshev多项式)的特征函数来近似任何平滑函数，就会出现谱精度现象[7]。

小波分析是数学研究中的一个新兴领域，在数学、工程和金融等领域得到了广泛的应用。小波的重要性质是紧支持性、正交性、正则性、标准正交性、对称性和良好的逼近精度。小波是由称为母小波的单个函数的扩张和平移构成的函数族[8]。在基于小波的逼近方法中，有两个重要的改进方法:增大小波族的阶数和增大小波的分辨率。当函数或其导数有不连续点时，小波逼近方法比傅里叶变换方法具有更高的阶收敛性。具体来说，Legendre小波是定义在经典Legendre多项式上的一种特殊小波[9]。由于Legendre小波的优点，它们被广泛地应用于求解偏微分方程和积分微分方程[10-11]。

在Black-Scholes模型中，股票价格的风险中性概率密度函数(PDF)是对数正态的。通过对从期权价格中提取风险中性PDF的研究，现有的方法主要可以分为参数和非参数两大类。参数化方法需要对变量之间的关系或资产收益分布的统计性质做一定的假设。显然，Black-Scholes模型就属于这一类。在非参数模型中，对基础资产价格的随机过程、期权定价函数或收益分布没有事先的限制。关于参数和非参数方案的完整综述，见Liu等人(2019)[12]。期权被认为包含风险中性PDF或风险中性矩生成函数(MGF)的独特信息。在文献中，已经提出了几种风险中性PDF估计方法，例如，基于傅里叶的数值积分[13]、高斯变换[14]、小波方法[15]，并在其中引用。Liu等人(2019)对风险中性MGF的小波方法进行了实证研究，并与各种成熟模型进行了比较[12]。然而，非参数模型比参数模型更灵活，但在许多情况下，它们需要(大量)交易期权价格样本。

风险中性测度是一种数学结构，通过期望算子对所有或有权益进行定价。这些可能的措施对应一个PDE，其中支付函数是相应PED的初始条件。然而，大多数期权定价问题在执行价格处存在非平滑支付或不连续的导数，但可以采用适当的数值方法求解相应的偏微分方程。由于数值PDE方法的优点是可以很容易地考虑复杂和奇异的收益。Black-Scholes偏微分方程的数值解通常采用有限差分方法[16]。在有限差分方法中，通过采取足够小的步长来保持方法的稳定性，解决问题的计算成本大大增加。因此，近年来，人们开始考虑时间或空间的半离散技术来计算Black-Scholes偏微分方程的数值解，如基于空间(或时间)有限差分的方法和基于时间(或空间)函数逼近的方法。例如，基于有限差分和三次B样条函数的方法[17]、拉普拉斯变换有限差分法[18]、紧致有限差分法[19]。

本文提出了一种基于有限差分和Legendre小波逼近格式的组合方法来求解Black-Scholes PDE(1)。将空间离散成等网格，并使用空间导数的有限差分公式，然后，采用Legendre小波逼近时间。本文推导了Legendre小波积分算子的矩阵结构，该算子迄今为止被广泛使用，但没有可靠的证明[11]。另外，为了使用到期时t=T的支付函数，求得了另一个运算矩阵，它是由已知上限的Legendre小波的不定积分得到的。利用有限差分、截断的Legendre小波级数展开和相应的积分运算矩阵，将求解偏微分方程问题简化为求解Sylvester方程。通过两种算法对欧式看涨期权和看跌期权的估值进行了简化。算例结果表明，与文献方法相比，该方法易于实现，具有较高的执行速度。本文还证明了所得到的Sylvester方程具有唯一解。数值结果表明，该方法具有较高的精度。此外，为了得到一个合适的解，不需要选择非常小的步长，并且只需要在Legendre小波序列中少量的基函数。

1 函数逼近

1.1 Legendre多项式

著名的Legendre多项式Pm(x)是奇异Sturm-Liouville问题的特征函数[7]：

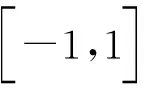
其中，P0(x)=1，P(x)=x。

关于勒让德多项式的一些性质如下：

Pm(±1)=(±1)m，

(4)

对于m=-1，P-1≡0，对于m=0,1,…,

(5)

1.2 Legendre小波

小波是由母小波的扩张和平移构成的函数族。当膨胀参数a和平移参数b连续变化时，有如下连续小波族[20]:

函数Ψk,n(t)形成L2(R)的小波基。当a0=2，b0=1时，函数Ψn,m(t)形成标准正交基。

ψn,m(t)=

(6)

系数cn,m为

如果式(6)中的无穷级数被截断，则可表示为

矢量C和Ψ(t)为

(7)

2 Legendre小波的积分算子矩阵

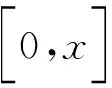
根据式(5)，可以验证，

因此，

因此，Legendre小波Ψn,m(t)可以写成

(8)

和Legendre多项式相似，Ψn,-1(t)=0。

P为2k-1M×2k-1M的积分算子矩阵，如下:

(9)

其中L和F是M×M的矩阵，如下所示:

证明

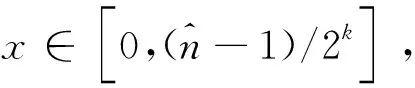
(10)

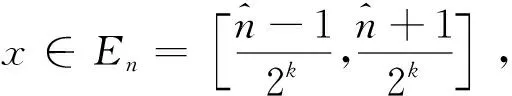
(11)

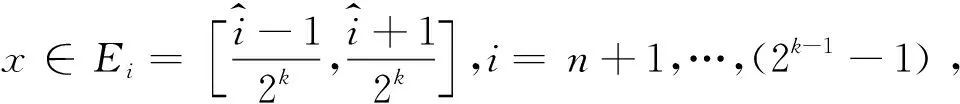
(12)

因此，结合式(10-12)可得

(13)

使m≠0，已知

(14)

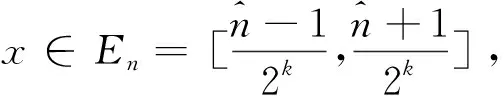
结合式(8)，可得

(15)

另外，通过式(4)，可得

(16)

因此，结合式(15)和式(16)，可得

(17)

(18)

因此，对于m>0，结合式(14),(17)和(18)，可得

(19)

采用式(13)和(19)，可得

⋮

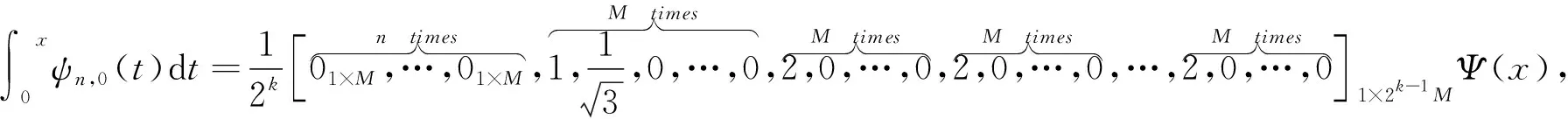
同样，根据式(19)可得

(20)

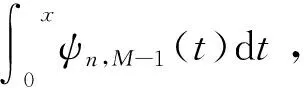
那么，

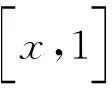
(21)

其中L和F是M×M的矩阵，如式(22)所示:

(22)

F的定义如定理1所示。

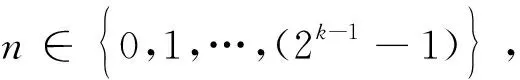
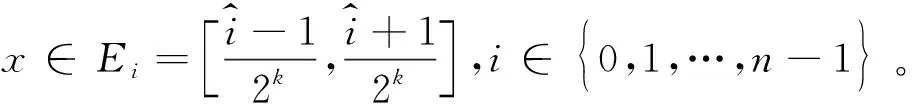
(23)

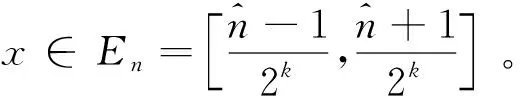
(24)

(25)

因此，结合式(23-25)可得

(26)

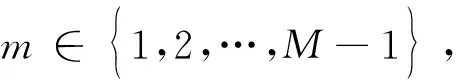
(27)

结合式(8)，可得

(28)

另外，通过式(4)，可得

(29)

因此，结合式(28)和(29)可得

(30)

而且，明显的是

(31)

因此，对于m>0，结合式(27)，(30)和(31)可得

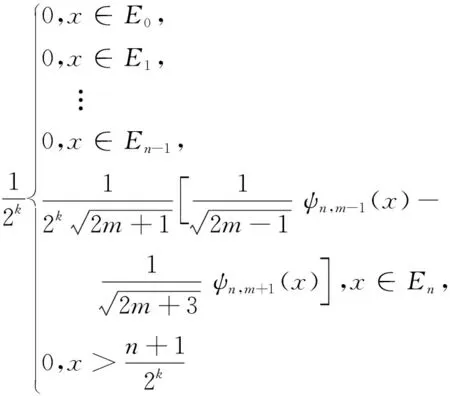
(32)

通过式(26)和(32)可得，进一步地，从式(32)可知

(33)

对于用基向量ψ(x)，必须消除式(33)中的项ψn,M(x)。因此，

可得

…

下面，我们利用有限差分和Legendre小波方法的组合方法，得到了计算欧式看涨和看跌期权的Black-Scholes微分方程的数值解。

3 欧式期权定价

在本节中，我们得到满足以下Black-Scholes PDE的欧式期权的值：

(34)

其中，r为无风险率，σ为股票价格S的波动率，V(S,t)为t时刻和股票价格S的期权价值，设E为行权价格。已知看涨期权的收益函数是

V(S,T)=max(S-E,0)，

(35)

看跌期权的收益函数为

V(S,T)=max(E-S,0)，

(36)

式(37)给出了欧式看涨期权的边界条件，

V(0,t)=0 ，

V(S,t)～S-Ee-r(T-t),S→∞，

(37)

式(38)给出了欧式看跌期权的边界条件，

V(0,t)=Ee-r(T-t)，

V(S,t)=0,S→∞，

(38)

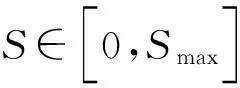
将Si代入式(34)，可得

为简化，设置Vi(t)=V(Si,t)，并且通过利用一阶导数∂V/∂S和二阶导数∂2V/∂S2的有限差分公式，对于i=1,2,…,N-1，可得

(39)

使

那么，将式(39)转化为常微分方程(ODE)组

(40)

其中，

(41)

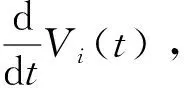
(42)

通过积分式(42)，可得

(43)

结合式(40),(42),(43)可得

(44)

其中，

R(t)=AV(1)+b(t),

(45)

并且，

接下来考虑式(44)分别来评估看涨期权和看跌期权。

3.1 看涨期权

对于欧式看涨期权，式(45)中的右侧向量R(t)可由式(35)和式(37)通过设置得到

Vi(1)=V(Si,1)=max(iΔS-E,0),

V0(t)=V(S0,t)=V(0,t)=0,

(46)

VN(t)=V(SN,t)=V(Smax,t)=Smax-Ee-r(T-t).

(47)

设定，

R(t)=(R1(t),R2(t),…,RN-1(t))T,

(48)

那么，通过Ri(t)的Legendre小波展开，可得

(49)

因此，结合式(44)和式(49)可得下列Sylvester方程

(50)

其中，

通过求解sylvester方程(50)，再结合式(43)，欧式看涨期权的近似值为

(51)

算法 1：t时刻欧式看涨期权

InputN,M,k

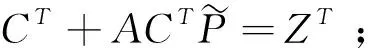
3：for i=1,2,…,N-1 do

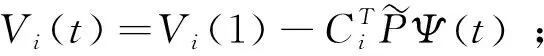
5：end for

算法1表明，该方法易于实现，具有较高的执行速度。

算例1考虑式(34)Black-Scholes PDE在r=0.2,σ=0.25,E=10和Smax=20下的欧式看涨期权定价。对于ΔS=1和2，在k=2，M=3时用本文提出的方法求解了这个问题。图1给出了看涨期权V(Si,0)的近似解和精确解式(2)。

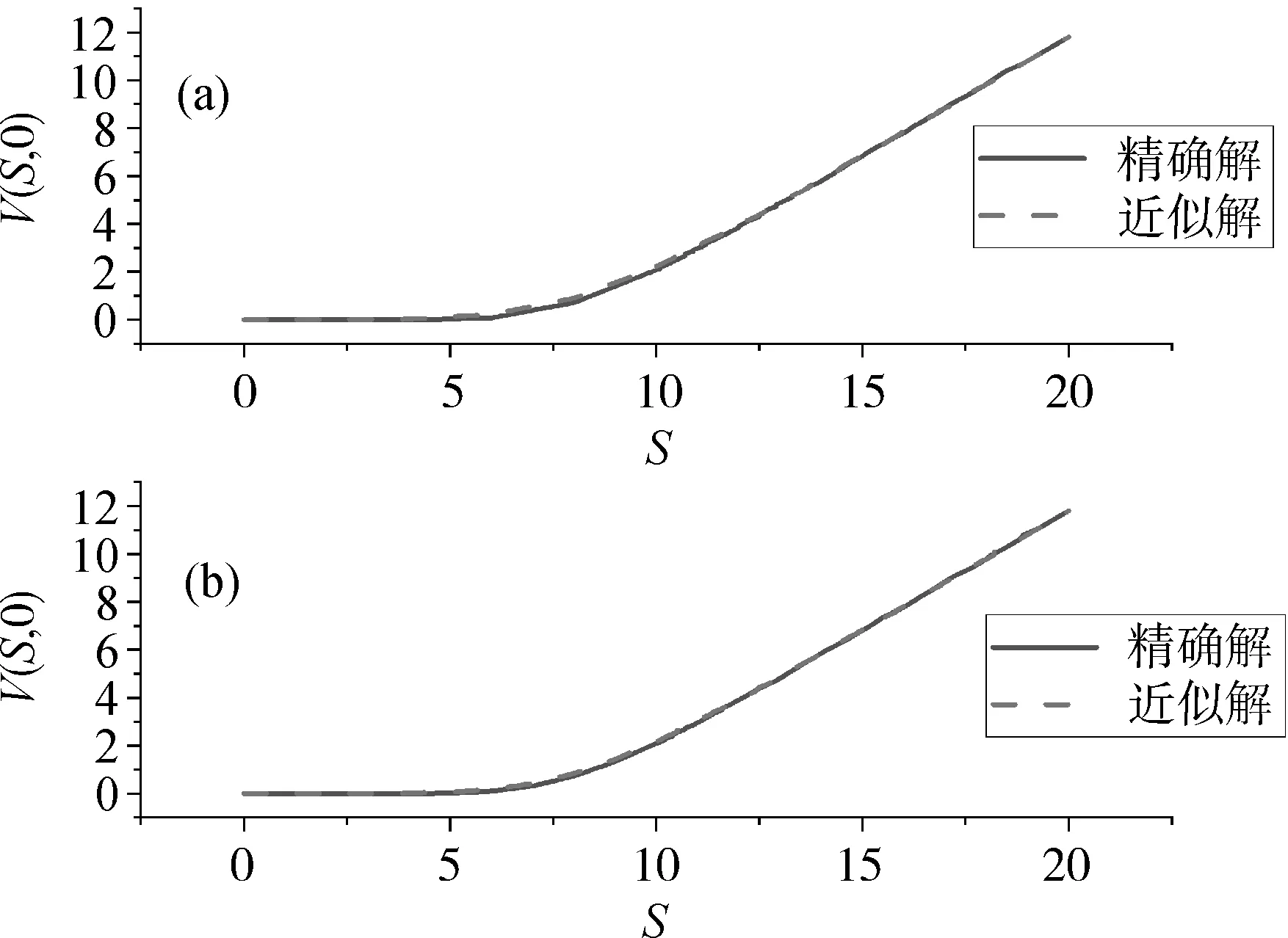
图1 对于空间步长(a) ΔS=2和(b)ΔS=1，算例1中采用本文所提方法时Black-Scholes PDE在M=3和k=2下精确解和近似解的比较

从图1中可以看出，尽管有其他方法，如有限差分法，ΔS并不需要非常小。而且，在Legendre小波的近似中，k和M不需要很大，这样可以减少计算成本。为了表明所提方法的数值稳定性，空间步长ΔS对计算精度的影响如图2所示。

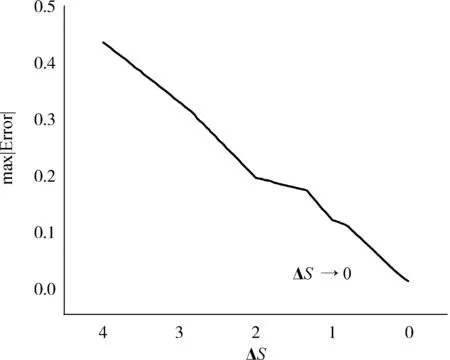
图2 在不同的空间步长ΔS下，例1中在M=3和k=2下采用本文所提方法时，Black-Scholes偏微分方程的精确解与近似解之间的最大绝对误差

3.2 看跌期权

对于欧式看跌期权，式(45)的右边向量R(t)可由式(36)和(38)通过设置得到

Vi(1)=V(Si,1)=max(E-iΔS,0),

V0(t)=V(S0,t)=V(0,t)=Ee-r(T-t),

(52)

VN(t)=V(SN,t)=V(Smax,t)=0,

(53)

使

R(t)=((R1(t),R2(t),…,RN-1(t))T,

(54)

那么，可得

(55)

因此，根据式(44)和式(55)，可得Sylvester方程式

(56)

其中，

通过求解式(56)，并根据式(43)，可得欧式看跌期权在时间t的近似值

(57)

算法2给出了欧式看跌期权的评估方法，如下所示:

算法2：t时刻欧式看跌期权

InputN,M,k

Output European put optionV(Si,t)

3：for i=1,2,…,N-1 do

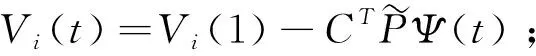
5：end for

算例2考虑Black-Scholes PDE式(34)在r=0.2,σ=0.25,E=10和Smax=20下的欧式看跌期权定价。对于ΔS=1和2，在k=2，M=3时用本文提出的方法求解了这个问题。图3给出了看跌期权V(Si,0)的近似解和精确解。

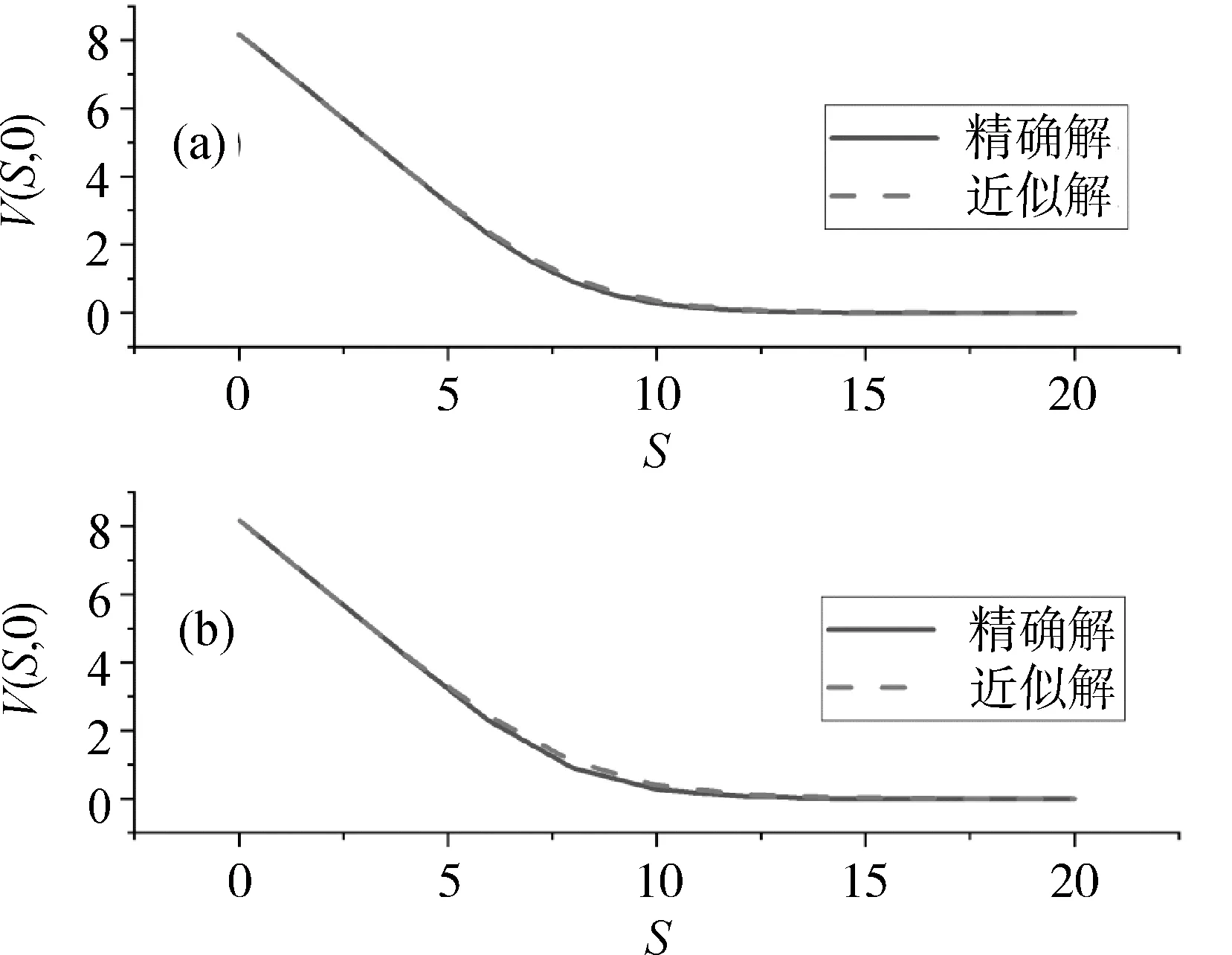
图3 对于空间步长(a)ΔS=2和(b)ΔS=1，算例2中采用本文所提方法时Black-Scholes PDE在M=3和k=2下精确解和近似解的比较

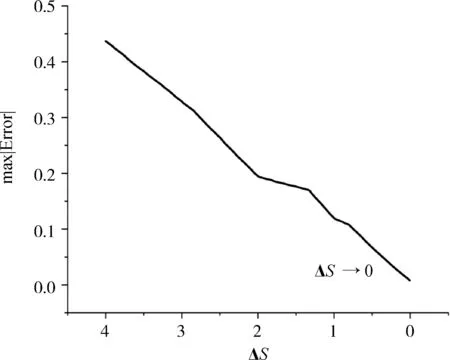
图4 在不同的空间步长ΔS下，例2中在M=3和k=2下采用本文所提方法时，Black-Scholes偏微分方程的精确解与近似解之间的最大绝对误差

3.3 所得Sylvester方程解的存在唯一性

接下来，证明了Sylvester方程式(50)和(56)有唯一解。

定理3给出了在(Veselic 1979)[22]中证明的某三对角矩阵的惯性。

定理3对于三对角矩阵

其中，ak，bk，ck是实值，l是虚数单位，a1≠0，akck≠0，k=2,…,n。那么，ln(T)=ln(D)，其中，D=diag(a1,a1a2c2,a1a2a3c2c3,…,a1…anc2…cn)。

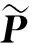
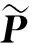
引理1定义式为(41)的A的所有特征值都是不同的实数，且大于或等于无风险率r。

证明对于三对角矩阵A，如式(41)所示，由于γiαi+1>0，i=1,2;…,N，A的特征值λA是不同的实数[22]。而且，通过Gershgorin圆定理[23]可以很容易地证明，λ(A)≥r。

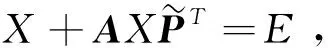
证明

(58)

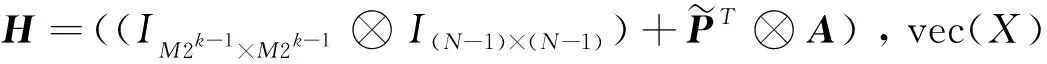
推论2欧式看涨期权和看跌期权的近似如式(51)和(57)所示，存在并且是唯一的。

证明定理4的一个推论是Sylvester方程式(50)和(56)，用所提方法得到的近似欧式看涨期权和看跌期权都有解，且解是唯一的。

4 结语

股票交易者广泛使用股票期权定价来对冲金融市场中的风险，利用期权来调整交易策略和投资组合。欧式看涨期权和看跌期权是两种主要的期权定价问题，可由布莱克-斯科尔斯偏微分方程(Black-Scholes partial differential equation, PDE)推导。本文研究了Black-Scholes偏微分方程的数值解。给出了Legendre小波积分算子的矩阵结构。另外，为了采用到期时的支付函数t=T，得到了另一个运算矩阵，它是由已知上限的Legendre小波的不定积分得到的。利用有限差分、截断的Legendre小波级数展开和相应的积分运算矩阵，将Black-Scholes微分方程简化为Sylvester方程。本文通过两种算法对欧式看涨期权和看跌期权进行了评估。算法表明，与文献方法相比，该方法易于实现，具有较高的执行速度。同时证明了所得到的Sylvester方程具有唯一解，数值结果表明所提出的方法具有较高的精度。与文献方法相比，为了得到一个合适的解，该方法不需要选择非常小的步长，而且只需要Legendre小波序列中少量的基函数。