直觉模糊环境下概率优势粗糙集的增量式更新算法
2022-03-05苑红星
苑红星
(安徽大学网络信息中心,安徽 合肥 230601)
1 引言
粗糙集是集理论对研究信息不足和不完整智能信息系统的一种扩展,最早于1982年由波兰学者Pawlak提出[1]。作为一种新的数学工具来处理数据的模糊性和不确定性,粗糙集理论已成为数据挖掘的重要方法和工具。针对实际环境下各种应用数据类型,近年来学者们不断地对粗糙集理论进行扩展和改进。
为了解决信息系统属性值的排序问题,Greco等学者[2]根据优势关系建立了一种粗糙集方法。具体来说,通过考虑描述对象的优先级或通过个体属性进行选择,用偏好关系来描述优势关系的粗略近似。目前,基于优势关系的粗糙集方法受到了学者们的广泛关注和研究[3-7]。Wang等[8]学者针对直觉模糊数据环境构造了概率优势关系,并提出一种称之为直觉模糊概率优势粗糙集的模型,理论分析证明了该模型具有更高的近似性能和更广泛的泛化性能,进一步提升了优势关系粗糙集模型的应用范围。
然而,现实应用中产生的数据通常不是静态的,而是随着时间的推移逐渐演变,其中信息系统的对象增加和减少是信息系统最为常见的变化形式。例如,在电子医疗记录系统中,新增患者的记录使得信息系统的对象增加,康复出院的患者从记录中删除使得信息系统对象减少。由于信息系统的这种动态更新特性,传统的静态方法对更新后的数据进行模型再训练,难以满足实际的时效性需求。针对粗糙集各种理论与模型,学者们提出了多种的增量式方法来解决这种信息动态更新的问题。例如,刘桂枝[9]提出了一种不完备混合型数据的增量式属性约简;Kumar等[10]学者提出了一种基于模糊粗糙近似方法的增量式特征选择算法;Huang等[11]学者构造出条件熵的增量式策略,提出多源数据的属性约简更新;闫振超等[12]学者针对混合型数据提出一种属性约简的增量式更新;Yang等[13]学者提出了属性组的增量式属性约简算法,同时也提出了一种增量式属性约简的统一模型[14],使得增量式属性约简的研究形成了完备的框架体系。在模型的增量式更新方面,Yang等[15]学者提出了模糊概率决策粗糙集的三支决策更新模型;袁路妍等[16]学者提出了双论域数据环境下决策粗糙集的增量式更新;薛占熬等[17]学者在其基础上,进一步地提出了双论域模糊概率粗糙集的增量式更新;梁艳玲等[18]学者在区间值信息系统下提出了一种决策粗糙集的增量式更新;Ge等[19]学者在不完备混合型信息系统下研究了增量式概率近似粗糙集模型,同时进一步研究了不完备邻域信息系统的决策粗糙集三支决策的增量式更新[20]。总之,目前粗糙集的增量式研究受到了学者们越来越多的关注。
然而,Wang等[8]学者提出的直觉模糊概率优势粗糙集模型,仅适用于静态的数据集,因此本文将针对该模型,提出一种增量式的更新方法。矩阵是设计增量式学习的常用工具[11,16,20],本文将采用矩阵的架构来构造模型的增量式更新。文中首先通过关系矩阵重新表达了直觉模糊概率优势关系,并通过相应的矩阵运算得到了直觉模糊概率优势粗糙集的特征向量形式;然后基于矩阵的更新策略,分别提出了对象增加和减少情形下,直觉模糊概率优势粗糙集的增量式更新。理论分析结果表明,该增量式更新基本上依赖于变化的对象集,而对原始的数据有很少的依赖,因此具有较高的增量式更新效率,实验分析结果同样证明了该方法的有效性。
2 基本理论
在本章节,主要介绍直觉模糊集和直觉模糊环境下的概率优势粗糙集模型[8]。
定义1[21]设U为一个论域集,那么对于论域子集Y⊆U下的直觉模糊集定义为
定义5[8]设直觉模糊信息系统定义为IFIS=(U,AT=(C∪D),V),其中U为直觉模糊信息系统的论域,C,D分别为直觉模糊信息系统的条件属性集和决策属性集,V为值域且属性值均为直觉模糊集。定义B⊆C确定的直觉模糊概率优势关系为
其中δ称为直觉模糊概率优势关系的优势可信度。
定义6[8]设直觉模糊信息系统IFIS=(U,AT=(C∪D),V),B⊆C确定的直觉模糊概率优势关系为,∀x∈U在下确定的概率优势类为
定义7[8]设直觉模糊信息系统IFIS=(U,AT=(C∪D),V),决策对象集划分为为信息系统的上联合优势决策集,属性子集B⊆C,定义φ⊆U在概率优势关系下的概率优势下近似集和上近似集分别为
文献[8]提出的直觉模糊环境下的概率优势粗糙集模型进一步丰富了优势粗糙集的拓展与应用。
3 直觉模糊概率优势粗糙集的矩阵表示
矩阵在表示和重构粗糙集模型方面发挥了很重要的作用[11,16,20],在本节,将基于矩阵的方法去重新构建直觉模糊概率优势粗糙集模型。
定义8设直觉模糊信息系统IFIS=(U,AT=(C∪D),V),|U|=n,B⊆C确定的直觉模糊概率优势关系为,定义对应的直觉模糊概率优势关系矩阵为
下文中,在不引起混淆的情形下,我们使用MU×U简单表示
定义9设直觉模糊信息系统IFIS=(U,AT=(C∪D),V),|U|=n,对象集X⊆U的特征向量XU定义为
基于定义8和定义9,可以得到如下性质:
(3)根据定义6和定义9可直接证明成立。
定义10给定对象集X⊆U的特征向量XU=(α1,α2,…,αn)T,“T”表示转置,那么定义
通过定义10可以看出,|MU×U|是一个n×1矩阵,其中|MU×U|的第i个元素为MU×U第i行所有元素值的累加和。
根据定义8至定义10,我们可以进一步得到概率优势下近似集和上近似集的矩阵形式表达。
定义11给定对象集X⊆U的特征向量XU=(α1,α2,…,αn)T,定义XU的向下取整函数IntDown和向上取整函数IntUp分别为
证毕。
通过定理1可以看出,利用矩阵的方法计算直觉模糊概率优势粗糙集的上下近似集,具有很强的系统性和很好的便利性,这为直觉模糊概率优势粗糙集的增量式计算奠定了良好的基础。
4 直觉模糊概率优势粗糙集的增量式更新
在第3节中,我们提出了直觉模糊概率优势粗糙集的矩阵表达形式,本节中,将利用矩阵的形式提出信息系统对象变化时直觉模糊概率优势粗糙集的增量式更新方法。
对于对象动态变化的直觉模糊信息系统,设变化前的信息系统为IFIS=(U,AT=(C∪D),V),上联合优势决策集为φ,属性子集B⊆C确定的概率优势关系为,如果在某个时刻,信息系统增加了对象集U+,那么更新后的信息系统表示为IFIS'=(U',AT=(C∪D),V),这里的U'=U∪U+,对应的上联合优势决策集更新为φ'=φ∪φ+,φ+⊆U+,此时属性子集B⊆C确定的新概率优势关系表示为.如果在某个时刻,信息系统删除了对象集U-,那么更新后的信息系统表示为IFIS'=(U',AT=(C∪D),V),这里的U'=U-U-,φ-⊆U-,对应的上联合优势决策集更新为φ'=φ-φ-,此时属性子集B⊆C确定的新概率优势关系表示为
4.1 对象增加时直觉模糊概率优势粗糙集的增量式更新
定理2设变化前的信息系统为IFIS=(U,AT=(C∪D),V),上联合优势决策集φ对应的特征向量为,当增加对象集U+更新至IFIS'=(U',AT=(C∪D),V),此时新的上联合优势决策集φ'=φ∪φ+对应的特征向量增量式更新为
这里的表示φ+在对象集U+下的特征向量。
证明:根据定义9可以直接得到定理2成立。
接下来将研究直觉模糊概率优势关系矩阵的增量式更新。
定理3设直觉模糊信息系统IFIS=(U,AT=(C∪D),V),|U|=n,属性集B⊆C确定的直觉模糊概率优势关系为,对应的关系矩阵为MU×U,当信息系统增加对象集U+更 新 至IFIS'=(U',AT=(C∪D),V),|U+|=n+,不 妨 设U+={xn+1,xn+2,…,xn+n+},新的直觉模糊概率优势关系为,那么对应的关系矩阵MU'×U'增量式更新为
这里的
在定理2和定理3关于优势决策集特征向量和直觉模糊概率优势关系矩阵增量式更新的基础上,接下来可以进一步得到概率优势下近似集和上近似集的增量式更新。
证毕。
4.2 对象减少时直觉模糊概率优势粗糙集的增量式更新
定理5设变化前的信息系统为IFIS=(U,AT=(C∪D),V),上联合优势决策集φ对应的特征向量为,当删除对象集U-,这里不妨设U-={xn-n-+1,xn-n-+2,…,xn},更新后的信息系统为IFIS'=(U',AT=(C∪D),V),U'=U-U-,此时新的上联合优势决策集φ'=φ-φ-对应的特征向量即为删除的第n-n-+1,n-n-+2,…,n个元素,即
证明:根据特征向量的定义可以直接得到定理5成立。
接下来将研究直觉模糊概率优势关系矩阵的增量式更新。
定理6设直觉模糊信息系统IFIS=(U,AT=(C∪D),V),|U|=n,属性集B⊆C确定的直觉模糊概率优势关系为,对应的关系矩阵为MU×U,当删除对象集U-更新至IFIS'=(U',AT=(C∪D),V),其中U-={xn-n-+1,xn-n-+2,…,xn},新直觉模糊概率优势关系为,那么关系矩阵MU'×U'为删除MU×U的 第n-n-+1,n-n-+2,…,n行 和 第n-n-+1,n-n-+2,…,n列,即
证明:根据直觉模糊概率优势关系的定义,对于1≤i≤n-n-,1≤j≤n-n-,若,那 么,因此定理6成立。
在定理5和定理6关于优势决策集特征向量和直觉模糊概率优势关系矩阵增量式更新的基础上,接下来可以进一步得到概率优势下近似集和上近似集的增量式更新。
定理7设直觉模糊信息系统IFIS=(U,AT=(C∪D),V),|U|=n,属性集B⊆C确定的直觉模糊概率优势关系为,对应的关系矩阵为MU×U,上联合优势决策集φ对应的特征向量为,并且φ的上下近似集特征向量对应的
5 非增量式算法与增量式算法
在第3节中,我们通过矩阵的形式去重新表示了直觉模糊概率优势粗糙集,针对信息系统对象增加和减少的情形,接下来将提出矩阵形式直觉模糊概率优势粗糙集的更新算法,也称之为非增量式更新算法。
算法1:对象变化时基于矩阵形式的直觉模糊概率优势粗糙集非增量式更新算法。
输入:直觉模糊信息系统IFIS=(U,AT=(C∪D),V),上联合优势决策集φ,属性子集B⊆C,优势可信度δ;增加或减少对象集后新信息系统为IFIS'=(U',AT=(C∪D),V),新的上联合优势决策集φ'.
(1)计算φ'对应的特征向量.
(2)计算新信息系统下属性子集B⊆C概率优势关系对应的关系矩阵MU'×U'.
(3)计算
话说事情发生在老家镇的农资集贸市场里。秋播前夕,政府要调整市场经营格局:现有的农药农资、渔药渔需商店不再发散设置,按照新规划方案进行统一集中,形成一个“客买堆货”的农用渔业生产物资集贸区,利于经营,利于管理,方便农户。
在算法1所示的非增量式更新算法中,设|U'|=n+n+和|B|=b,那么算法1中步骤1的时间复杂度为O(n+n+),步骤2的时间复杂度为O(b·(n+n+)2),步骤3的时间复杂度为O((n+n+)2),步骤4和步骤5的时间复杂度为O(n+n+),因此整个算法1的时间复杂度为O(b·(n+n+)2).
在第4节中,我们通过矩阵的方法提出了直觉模糊概率优势粗糙集的增量式更新机制,接下来将针对信息系统对象增加和对象减少的情形,分别提出矩阵形式的直觉模糊概率优势粗糙集增量式更新算法。
算法2:对象增加时基于矩阵形式的直觉模糊概率优势粗糙集增量式更新算法。
输入:直觉模糊信息系统IFIS=(U,AT=(C∪D),V),上联合优势决策集φ,对应的特征向量,属性子集B⊆C,优势可信度δ,直觉模糊概率优势关系对应的关系矩阵;增加的对象集U+,新信息系统为IFIS'=(U',AT=(C∪D),V),新的上联合优势决策集φ'=φ∪φ+.
(1)计算φ+在对象集U+下的特征向量.
(2)在新信息系统IFIS'=(U',AT=(C∪D),V)下基于属性子集B⊆C计算优势关系矩阵MU×U和.
在算法2中,设|U|=n、|U+|=n+和|B|=b,那么步骤1的时间复杂度为O(n+),步骤2的时间复杂度为O(b(n·n++n+·n+)),基于定理4,步骤3的时间复杂度为O(n·n++n+·n+),步骤4和步骤5的时间复杂度为O(n+n+),因此整个算法2的时间复杂度为O(b(n·n++n+·n+)).
算法3:对象减少时基于矩阵形式的直觉模糊概率优势粗糙集增量式更新算法。
输入:直觉模糊信息系统IFIS=(U,AT=(C∪D),V),上联合优势决策集φ,对应的特征向量,属性子集B⊆C,优势可信度δ,直觉模糊概率优势关系对应的关系矩阵;删除的对象集U-={xn-p+1,xn-p+2,…,xn},新信息系统为IFIS'=(U',AT=(C∪D),V),新的上联合优势决策集φ'=φ-φ-.
(1)计算φ-在对象集U-下的特征向量.
(2)通过定理6基于MU×U增量式计算出新的关系矩阵MU'×U'以及.
(3)在新信息系统IFIS'=(U',AT=(C∪D),V)下基于属性子集B⊆C计算优势关系矩阵MU'×U-和.
在算法2中,设|U|=n和|U-|=n-,那么步骤1的时间复杂度为O(n-),基于定理6,步骤2和步骤3的时间复杂度为O(1),基于定理7,步骤4的时间复杂度为O((n-n-)·n-+n-·n-),步骤5和步骤6的时间复杂度为O(n-n-),因此整个算法3的时间复杂度为O((n-n-)·n-+n-·n-).
6 实验分析
为了证明本文所提出增量式更新算法的有效性,本节将通过对动态数据集增量式更新计算概率优势近似集来进行实验测试。表1所示的是本实验所使用的UCI数据集,这些数据集均为数值型类型,在实验时需要将数值型进行标准化至[0,1]。本文所研究的对象为直觉模糊集信息系统,为了构造这一数据类型,本实验将表1中数据集的属性值v作为隶属度,在[0,1-v]范围内随机选择数值作为非隶属度,这样可以完成数值型数据集的直觉模糊化。本实验所有实验算法通过matlab2015b进行编程实现,编码运行的硬件环境为英特尔i5 6500、3.2GHz处理器和8GDDR4内存的个人主机上。

表1 实验数据集
6.1 实验设计
在本文的实验中,类似于文献[16,17]的方法,需要将表1中的静态数据集进行动态化。我们将表1中每个完整的数据集按照对象集大致平均分成10等份,随机选择两份作为增量式增加更新的初始数据集,每次从剩余部分中选择一定份数添加至初始数据集,则构造出数据集的动态增加的变化环境,如果将完整数据集作为初始数据集,每次从中移除一定份数的数据集,便构造出数据集的动态减小的变化环境。然后分别将本文提出的非增量式算法与增量式算法进行概率优势近似集的动态更新,通过更新的时间来证明本文增量式算法的有效性。在本文所提出的增量式更新算法中,概率优势关系属性子集和可信度δ都是固定的量,本实验将属性子集设置为属性全集,可信度设为δ=0.7进行实验。
6.2 相同数据量变化时算法效率的比较
本节将进行直觉模糊信息系统对象等量动态变化时非增量式算法与增量式算法更新近似集的计算用时比较。对于等分的10份数据集,从随机的两份开始,每次更新时从剩余中只选择一份数据集进行添加,这样可以构造出8次等量动态增加。从原始数据集开始,每次选择一份进行依次删除,这样可以构造出8次等量动态减少,即数据集的更新变化量为原始数据集的10%。图1和图2分别所示的是数据集等量增加和等量减少时非增量式算法与增量式算法的概率优势粗糙集更新用时比较结果。

图1 各个数据集等量动态增加时更新效率比较
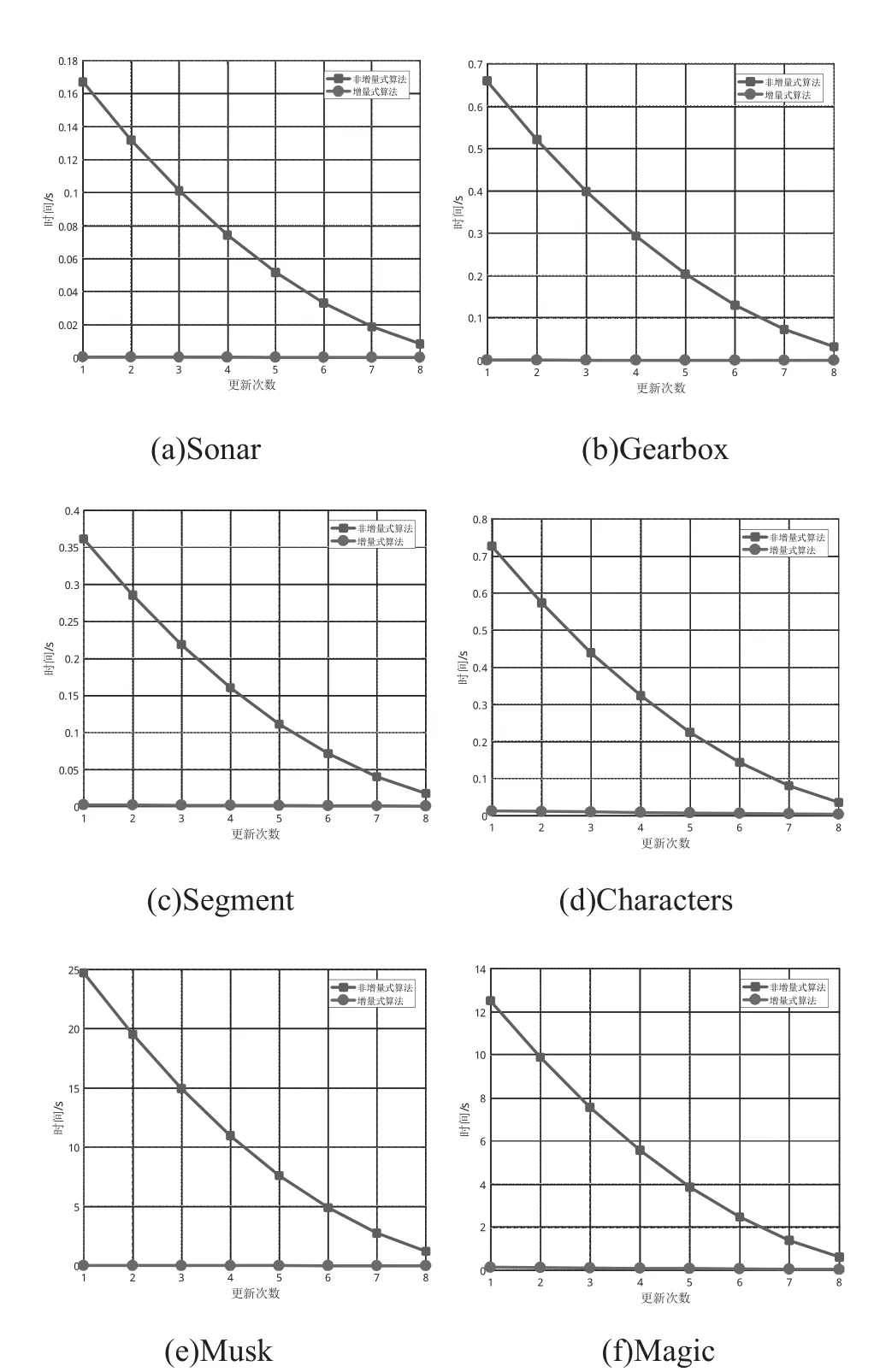
图2 各个数据集等量动态减少时更新效率比较
观察和分析图1和图2的实验结果,可以看出:
(1)随着数据集对象的等量逐渐增加,非增量式算法的更新用时迅速增加,而增量式算法的更新用时增加缓慢,且大幅度小于非增量式算法。
(2)随着数据集对象的等量逐渐减少,非增量式算法的更新用时从比较高的水平迅速减少,而增量式算法的更新用时很少,几乎可以忽略不计。
图1和图2表现出的实验结果,主要是由于非增量式算法基于当前数据集直接进行处理计算,其计算量与当前的数据量强相关,因此更新用时随数据变化很大,而增量式算法基于更新前数据集增量式计算,主要计算量集中在变化的数据上,因此数据集等量变化时,其所需的计算时间较少,并且变化得较为缓慢。
6.3 不同数据量变化时算法效率的比较
本节将进行直觉模糊信息系统对象非等量动态变化时非增量式算法与增量式算法更新近似集的计算用时比较。对于等分的10份数据集,随机选择两份开始,每次更新时分别从剩余中选择依次递增份数的数据量进行添加,例如,第一次添加一份数据集,第二次添加两份数据集,第三次添加三份数据集,依此类推,这样可以构造出8次非等量动态增加。从原始数据集开始,每次分别选择递增份数的数据集进行删除,例如,第一次删除一份数据集,第二次删除两份数据集,第三次删除三份数据集,依此类推,这样可以构造出8次非等量动态减少。图1和图2分别所示的是数据集非等量增加和非等量减少时非增量式算法与增量式算法的概率优势粗糙集更新用时比较结果。
观察和分析图3和图4的实验结果,可以看出:

图3 各个数据集非等量动态增加时更新效率比较

(1)随着数据集对象的非等量地逐渐增加,即每次增加的数据量越来越多,非增量式算法和增量式算法的更新用时都大幅度地增加,但是增量式算法更新用时少于非增量式算法。
(2)随着数据集对象的非等量地逐渐减少,即每次减少的数据量越来越多,非增量式算法的更新时间从开始比较高的时间量逐渐减小。而增量式算法的更新时间整体处于一个比较低的水平,大幅度小于非增量式算法,并且有逐渐增加的趋势。
图3和图4表现出的实验结果,主要是由于随着增加的数量越来越多,增量式算法对变化的数据进行更新计算,因此每次的计算量也越来越多,但是由于是增量式计算,因此每次的计算时间仍然小于非增量式算法。同理,对于数据集的非等量减少,每次减少的数量越来越多,因此图3增量式算法呈现出时间增多的趋势,但是整体大幅度小于非增量式算法。
6.4 实验总结
综合图1和图2数据集等量变化与图3和图4数据集非等量变化的实验结果,展现出了本文所提出的增量式算法在更新直觉模糊信息系统概率优势粗糙集上具有更高的更新效率,其更新用时大幅度少于非增量式算法,证明了本文所提出的增量式更新算法的有效性。
7 结语
直觉模糊概率优势粗糙集模型是粗糙集理论的重要扩展和泛化,然而,该模型仅适用于静态的数据集,为了满足现实应用数据的动态性,本文提出一种增量式的更新方法。文中首先通过矩阵的形式重新表达了直觉模糊概率粗糙集模型;然后利用矩阵的增量式更新策略,分别提出了对象增加和减少时直觉模糊概率优势粗糙集的增量式更新;最后提出了对应的增量式更新算法,实验分析结果证明了该方法的有效性。在接下来的研究中,我们将进一步探索直觉模糊概率优势粗糙集模型的增量式属性约简问题。
