基于双边滤波-BM3D算法的GPR图像去噪

王惠琴, 吕佳芸, 张 伟

(兰州理工大学 计算机与通信学院, 甘肃 兰州 730050)

地质雷达(ground penetrating radar,GPR)是利用电磁波对隧道、公路、桥梁等存在不同缺陷进行检测的一种无损检测技术,具有高分辨率、高效率、无损性以及雷达图像更直观等诸多优势[1].地质雷达在探测过程中,由于被探测地势可能存在着明显电性差异的局部不密实、空洞、厚度不足、钢筋缺失等缺陷[2],导致在图像中形成波形反射.然而,这些缺陷目标体形成的反射波不可避免地受到各类噪声和杂波的干扰,使缺陷目标体的细节信息被噪声掩盖,造成图像质量下降,从而影响图像的解译.因此,如何获得高质量的地质雷达图像成为地质雷达信号处理亟需解决的关键性问题.

目前,常见地质雷达图像去噪方法主要分为三大类,即空间域去噪、频率域去噪和空频域去噪[3].其中,空间域去噪利用目标像素领域特性进行去噪,常见方法有中值滤波[4]、非局部均值滤波(non-local mean,NLM)[5]、维纳滤波[6]、双边滤波[7]和形态学去噪法[8]等.采用空间域去噪算法虽然可以很好地保留地质雷达图像的边缘信息,但其中的细节信息会变得模糊,造成图像不够清晰.频率域去噪利用图像中的有用信号和噪声分布在不同频段的特点进行去噪,常见的方法主要有KL变换[9]和小波变换[10]等.虽然采用频率域方法可以有效去除地质雷达图像中的噪声,保留图像边缘和纹理信息,但它们也引入了由吉布斯现象[11]造成的振铃效应,严重影响了图像的主观视觉质量[12].空频域去噪是两种不同域中去噪算法的结合,其中最为典型的是三维块匹配(block matching 3D,BM3D)去噪算法[13].BM3D算法是一种在转换域中加强稀疏表达的图像去噪方法.虽然它在处理图像细节及高斯白噪声时效果较好,但在处理具有高对比度图像的边缘时,由于匹配块不能完整表示图像细节,致使图像的边缘会产生边缘振铃效应[14].

为了获得高质量的地质雷达图像,需要将噪声掩盖的缺陷目标体比较清晰地呈现.如果单一采用空间域、频率域以及空频域中的任意去噪方法,其去噪效果并不理想,或者可能会造成细节信息丢失以及目标体边缘模糊等.因此,所提算法充分利用双边滤波能够保持缺陷目标体边缘的优势,将其与BM3D算法相结合,提出了一种融合去噪算法,达到增强地质雷达图像的目的.

1 基本原理

1.1 双边滤波

(1)

其中：F(i,j)为领域像素点(i,j)的灰度值；Z为所选滤波器尺寸,滤波领域大小为(2Z+1)×(2Z+1)；W(a,b,i,j)为滤波器的权重系数,通常定义为

W(a,b,i,j)=U(a,b,i,j)R(a,b,i,j)

(2)

U(a,b,i,j)、R(a,b,i,j)分别为空域核函数和灰度核函数：

(3)

εU、εR分别为空间邻近度因子和灰度相似度因子;F(a,b)为中心像素点(a,b)的灰度值.

从式(2)可以看出,双边滤波的权重系数是式(3)的非线性组合.其中,εU、εR是影响滤波器效果的关键性因素.当两个影响因子取值过大时,双边滤波就会转换为均值滤波；反之,当取值过小时,达不到平滑图像的效果[16].

1.2 BM3D算法

BM3D算法是将噪声图像分割成尺度相同的图像块,并利用图像块间的相似性进行去噪的一种三维滤波算法.该滤波算法主要分为基础估计和最终估计两个阶段.这两个阶段都包含相似块匹配、三维协同滤波、聚合3个基本步骤,二者不同的是协同滤波分别使用硬阈值滤波和维纳滤波.

1) 基础估计

(4)

因此,可依据式(4)定义的匹配块与参考块间欧式距离判断该匹配块是否为相似块.当匹配块与参考块的距离小于固定阈值时,认为该匹配块为相似块,否则,不是相似块.依据该判断准则,并选取相似块间的最大欧式距离λht为阈值,则可得到参照块O的匹配块集合为

(5)

其次,对式(5)中的匹配块集合进行排序得到大小为Ω×Ω×Sht的三维矩阵OSht,并对该三维矩阵进行三维小波硬阈值变换.由于硬阈值滤波不仅能加强相似块的稀疏性,而且能降低相似块的噪声,因此通过对变换域系数进行硬阈值收缩处理来大幅度降低相似块中的噪声.将小波硬阈值变换后的矩阵再经三维逆变换后即可得到图像匹配块组的估计:

(6)

由于在图像块匹配过程中每个匹配块组的相同像素点都有多个估计值,因此需对图像中的每个像素点进行加权平均,即进行聚合处理.假设基础估计阶段图像匹配块组中第il个图像块在(i,j)位置上的像素估计为Ηil-ht(i,j),经过加权平均处理后,得到其基本估计为

(7)

其中:χil(i,j)为图像相似块的特征函数;Εht为每个匹配块组中相似块的个数;Wht为硬阈值变换后矩阵中所有非零元素权重的大小,即

(8)

σ2为噪声方差;Ψh为硬阈值变换后矩阵中所有非零元素的个数.

2) 最终估计

(9)

其中:λwie为设定的最大欧式距离阈值;Owie×Owie为图像尺寸.

将式(9)中匹配块集合进行排序得到大小为Owie×Owie×Swie的三维矩阵OSwie,经三维变换后,再采用维纳滤波将噪声图像形成的三维矩阵进行系数放缩.由于维纳滤波具有统计特性,使得滤波后形成的三维矩阵与噪声图像形成的三维矩阵在统计意义上的误差最小,因此,采用维纳滤波对三维矩阵进行点对点的系数收缩即可达到还原图像细节纹理的目的.在此基础之上,再将该矩阵经三维逆变换即可得到匹配块集合的估计值为

(10)

其中:WSwie为维纳滤波的收缩系数.在该部分引入维纳收缩的方法,其实质上是根据基础估计图像上变换系数的功率谱来对原始有噪声图像的变换系数进行收缩.因此,能够较好地滤除低频系数中的噪声能量,并最大限度地保留原本属于无噪声图像的那部分高频系数.依据文献[17],其表达式为

(11)

和基础估计相似,在完成三维协同滤波之后需要对其进行聚合处理.只是此时的加权权重取决于维纳滤波的权重系数和噪声方差,即权重系数为

(12)

依据文献[18],经加权平均处理后最终估计结果为

(13)

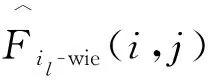
BM3D算法通过基础估计和最终估计后的增强图像达到了很好的去噪效果,尤其是图像中的细节纹理得到了很好的还原.

2 联合去噪算法

实际检测目标中可能存在的空洞、不密实及钢筋缺失等缺陷主要以反射波的形式呈现在地质雷达图像中.但是,在实际探测过程中由于背景噪声等因素的影响,使图像中的反射波被噪声掩盖,难以准确判断反射波的位置,因此,需对采集到的图像进行去噪处理.双边滤波能达到保边去噪的目的,但对高斯噪声的去除并不理想.BM3D去噪算法具有保留图像细节、有效去除高斯白噪声的优点,然而在处理高对比度的图像时,会使得图像边缘出现振铃现象.基于此,本文将双边滤波和BM3D算法相融合，提出双边滤波-BM3D联合去噪算法,并将该算法用于地质雷达图像去噪,具体去噪流程如图1所示.

由图1可见,首先,将含噪的地质雷达图像按式(1)进行双边滤波处理.由于双边滤波具有良好的保边特性,所以处理后图像的边缘特征得到了较好的保留,但此时图像中的高斯白噪声依然存在.因此,为了消除噪声和保留图像中的细节纹理信息,将双边滤波后的图像再经BM3D算法进行去噪.具体算法步骤如下.

第一步：基础估计.双边滤波后的图像被分割成大小相同的图像块(本文设定为3×3),在以上图像块中以最大距离阈值λht进行相似块搜索.将搜索到的图像块按式(4)与参照块进行匹配分组.其中,最大距离阈值λht的选取是一个关键,本文通过反复实验得到其最佳最大距离阈值.然后分别将匹配的二维图像块和参照块自身整合成三维矩阵,图1中用白色R表示,并依据式(6)进行三维硬阈值滤波.将滤波后的信号再经三维逆变换后,依据式(7)进行聚合处理.此时基础估计阶段完成,图像中的噪点得到有效去除.

第二步：最终估计.第二步与第一步的不同之处在于块匹配时得到两个三维矩阵,其中一个是噪声图像形成的三维矩阵(图1中用白色R表示),另一个是由基础估计得到的三维矩阵(图1中用黑色R表示).将上述三维矩阵依据式(11)进行系数放缩得到相似图像块组,然后对其按式(13)进行聚合完成最终估计,从而还原了更多原始图像的细节纹理.

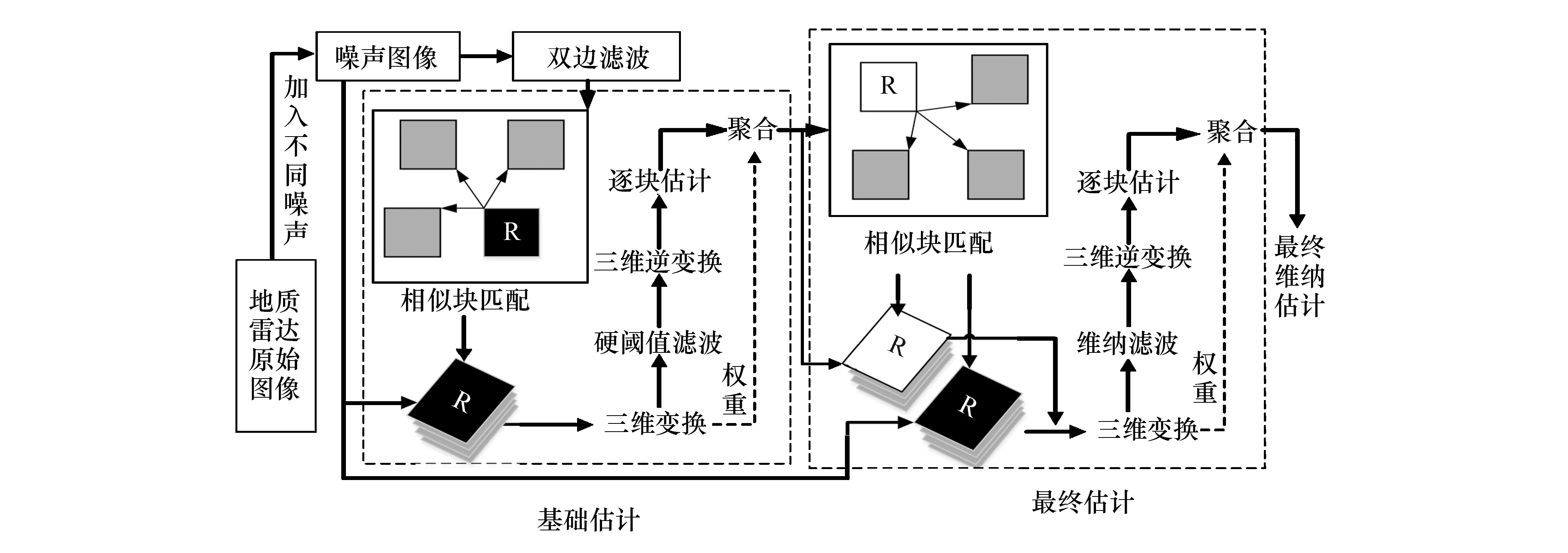
图1 双边滤波-BM3D算法去噪流程Fig.1 Denoising process of bilateral filtering BM3D algorithm

最后,将双边滤波保留的图像边缘特征、BM3D算法滤除的高斯白噪声和保留的图像细节纹理特征相融合,再经重构后得到最终的地质雷达去噪图像.

3 噪声滤除评价指标

为了更准确地评价地质雷达图像的去噪效果,本文选取峰值信噪比、结构相似性对不同去噪算法的去噪效果进行客观评价.

1) 峰值信噪比(peak signal-to-noise ratio,PSNR)

由于PSNR是噪声图像与去噪图像的对比,那么PSNR可被定义为

(14)

2) 结构相似性(structural similarity,SSIM)

由于PSNR是噪声图像与去噪图像的对比,并没有与原始图像进行对比,所以难以准确地说明去噪效果.因此,本文引入图像结构相似性来衡量去噪图像与原始图像的相似程度,并对参考图像的亮度、结构信息、对比度进行比较.两幅图像k和s的结构相似性定义为

(15)

4 实验结果分析

为了较好地说明双边滤波-BM3D算法对地质雷达图像的去噪效果,在无干扰的安静环境中,采用瑞典MALA系列地质雷达及800 MHz屏蔽天线对如图2所示的实测场景进行了检测,得到原始图像如图3所示.其中,实测场景1为某路边10 m墙,实测场景2为某隧道内8 m右拱腰.其次,将获得的原始图像作为纯图像,并在大小为512×256的原始图像中分别加入方差σ为1、5、10、20、30、40、50的高斯白噪声产生带噪图像.最后,对带噪图像分别采用双边滤波、BM3D算法以及双边滤波-BM3D算法进行去噪处理,其结果如图3、图4及表1所示.

图2 实验采集的缺陷场景

对图3a和图4a的实测场景图分别加入σ=10的高斯白噪声,获得带噪图像,其结果如图3b和图4b所示.

对图3b和图4b分别采用双边滤波处理,得到的结果如图3c和图4c所示.其中双边滤波的主要参数为：滤波领域大小取值为5×5,εU取值为2，εR取值为0.2.由图3c和图4c可见,图像中缺陷目标体的边缘得到了很好的保留,但此时图像中高斯白噪声的去除效果不佳.

图3d和图4d为图3b和图4b经过BM3D算法后的处理结果.经多次实验可得BM3D算法的主要参数为：λht取值为2 500,硬阈值取值为2.5.此参数下,BM3D算法对地质雷达图像的增强效果达到了最佳.由图3d和图4d可见,图像中高斯白噪声的去除效果较好,但是地质雷达图像中缺陷目标体变得模糊.

图3e和图4e表示对图3b和图4b经过双边滤波-BM3D算法后的处理结果.经多次实验可得该算法的主要参数为：滤波领域大小取值为3×3,εU取值为3，εR取值为0.2,λht取值为4 000,硬阈值取值为3.0.此参数下,该算法对地质雷达图像的增强效果达到了最佳.与双边滤波和BM3D算法的处理结果对比可知,所提算法不仅有效滤除了地质雷达图像中的高斯白噪声，而且在基本消除图像边缘振铃现象的情况下，较好地保留了图像边缘和细节纹理特征.

为了更好地说明本文所提方法的增强效果,对图3a和图4a分别加入σ为1、5、10、20、30、40、50的高斯白噪声,并计算与其对应的PSNR,其结果如表1所列.

从表1可见,随着σ的增加,所提联合去噪算法优于双边滤波和BM3D算法,特别是在小信噪比情况下,不仅有较高的PSNR值，而且SSIM值得到明显提升.同时,还发现所提算法的SSIM的最大值为0.858 8,即增强图像与纯图像的相似度约为86%.结合表1、图3e和图4e可以看出,双边滤波-BM3D算法去噪效果已经非常接近图3a、图4a的纯图像,这就说明所提算法可以有效去除噪声,较好地增强地质雷达图像.

图3 不同算法对地质雷达图像1去噪的效果

图4 不同算法对地质雷达图像2去噪的效果Fig.4 Denoising effect of different algorithms on GPR image 2

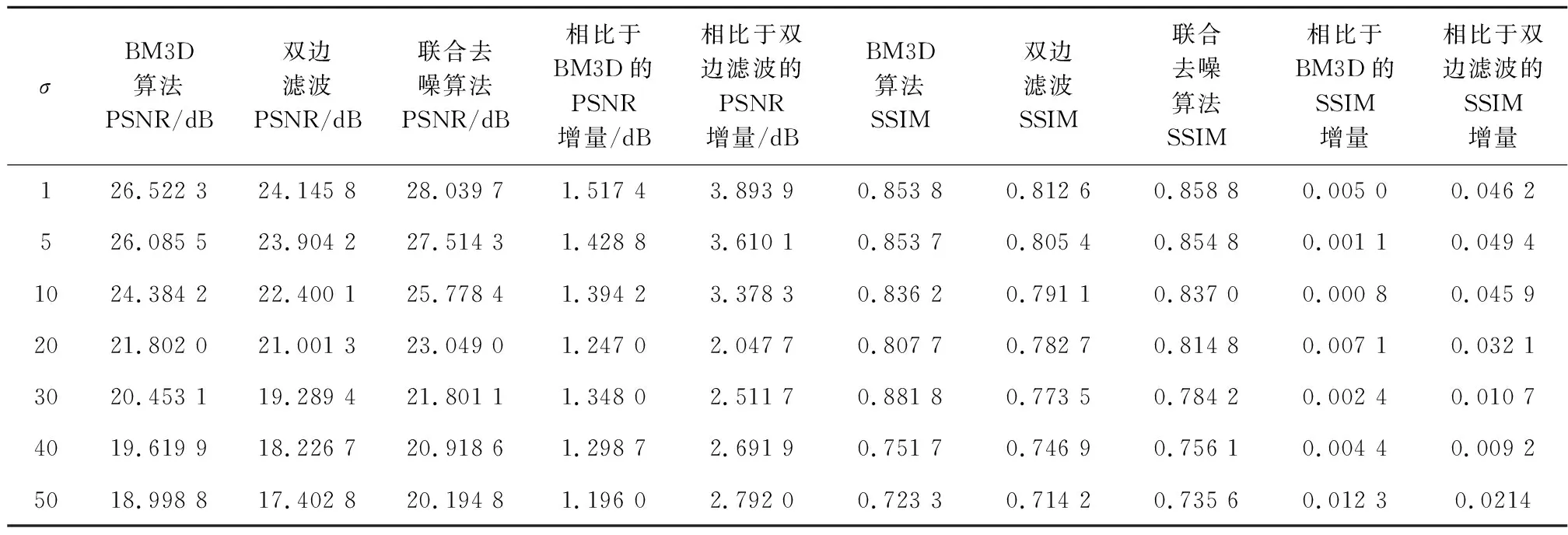
表1 不同σ值对应的PSNR和SSIM

5 结论

依据带噪地质雷达图像的特点,将双边滤波和BM3D算法相结合提出了一种联合去噪算法,并以实测的地质雷达图像为研究对象进行了验证.研究结果表明,与双边滤波、BM3D算法相比,联合去噪算法有效地保留了BM3D算法和双边滤波算法的优势,即保留图像细节纹理和去除高斯白噪声的同时,具有良好的边缘保持特性.从客观数据可以看出,较单一去噪算法,联合去噪算法的PSNR和SSIM的值都得到了较大提高；从主观视觉图像可以看出,联合去噪算法图像中缺陷目标体的边缘基本未出现振铃现象，细节纹理特征更加明显，并且噪点也得到了较大程度的滤除.