钻孔施工围岩破坏过程模拟研究

2022-03-05孔维库陈陆望李蕊瑞任星星

合肥工业大学学报（自然科学版） 2022年2期

孔维库, 陈陆望, 李蕊瑞, 任星星

(合肥工业大学资源与环境工程学院,安徽合肥 230009)

钻孔,尤其是竖直/垂直钻孔,被广泛应用于岩土和地质行业。随着钻头向深部钻进,围岩原位地应力增加,在孔壁处出现局部应力集中现象。当应力超过岩体屈服强度时,钻孔围岩进入塑性状态,开始产生塑性变形,裂纹开始发育[1]。随着深度增加,塑性区范围和塑性变形不断增大,围岩持续破坏,其稳定性降低。这将可能造成塌孔、卡钻、挤毁套管等工程事故,导致钻孔报废,造成严重经济损失[2-3]。近年来,随着钻探工程的施工深度逐渐加大,相关工程事故多有发生。因此，研究钻孔围岩的破坏机理及动态发育过程对于预测、评价深部钻孔围岩稳定性和减少工程损失显得尤为重要。

针对钻孔围岩稳定性问题,研究者通过现场探测、室内试验、理论分析和数值模拟等方法进行了大量研究。

理论方面,主要是基于不同假设和一些常用屈服准则,如MohrCoulomb准则[1,4]、Drucker-Prager准则[5-6]和统一强度理论[3-7]的围岩弹塑性解;还有研究进一步考虑围岩的损伤、应变软化等效应,建立了更具有针对性的围岩弹塑性模型[8-11]。数值模拟方面,通过设置不同应力加载条件,对钻孔围岩的应力和位移等变化规律进行模拟研究,发现孔周应力及位移随深度增加呈现出幂指数关系,且钻孔围岩破坏形式以剪切破坏为主;同时对一些影响钻孔围岩稳定性的因素进行了研究分析[12-18]。相关理论分析和数值模拟结果的准确性主要取决于是否选择能准确描述围岩力学性质的本构模型,从而求解围岩应力-应变特征和塑性区发育范围等。需要指出的是,岩石材料在应力达到峰值后,随着变形的继续增加,其强度将下降至较低的水平,进而发生明显的应变软化现象[19]。针对岩石这一特性,研究者通过试验研究、理论分析和数值模拟等方法研究了围岩的稳定性发现,相较于以往把岩石强度当成常数的方法,应变软化模型更符合围岩力学特征[11,20-23]。

试验方面,通过研究中间主应力对钻孔围岩变形和强度性质的影响,发现随着中间主应力系数增大,围岩强度先增大后减小,并基于修正Lade准则分析了塑性区的发育特性[24-25];通过研究高温高压下花岗岩钻孔围岩的变形失稳和力学特性,发现不同埋深下,围岩变形经过了微弱阶段、快速增长阶段和平稳阶段[26-27];通过模拟煤层钻进过程,得出不同试验条件下的孔周应力变化及孔壁、孔底破坏特征[28]。现场探测方面,超声波探测法、钻孔触探法及钻孔剪切法等[29]能够较为直观准确测得围岩原位强度,可为围岩稳定性评价提供可靠的参数。此外钻孔电视作为一种可视化技术,可直观地获得围岩的完整性、裂隙发育及破坏情况,在围岩稳定性分析及评价中得到广泛应用[30-32]。

这些研究手段各有优点,但也都具有一定的局限性。理论分析和数值模拟手段往往基于诸多假设,并把复杂的原位地质条件进行简化;模拟试验不一定能真实反映实际工程中复杂的钻孔围岩条件;现场探测成本较高且无法在施工前进行预测。以往围岩稳定性的研究往往采取单一方法,未能将多种手段结合综合研究钻孔围岩稳定性问题,研究结果相对较为片面。此外现有的研究多集中于讨论特定应力条件下围岩的破坏,不能很好地表现钻头钻进这一动态施工过程中应力条件改变下的围岩破坏过程。

结合已有的研究手段和研究成果,本文从钻孔物理模型试验出发,根据围岩材料在应力达到峰值后承载能力大幅下降这一特性,采用FLAC3D中的应变软化模型进行数值模拟,研究地下均匀应力场中竖直钻孔钻进过程的围岩破坏机理,揭示随载荷增加过程中围岩不同塑性变形阶段特征,并与淮北青东矿839工作面钻孔电视观测结果进行对比验证。研究旨在为地下钻孔工程顺利施工,降低工程损失提供一定的参考。

1 物理模型试验

1.1 物理模型试件

围岩的力学特征分析是开展数值模拟研究的前提,因此需要对围岩主要力学参数进行合理赋值。本研究团队前期选用石英砂、石膏、水泥、水等配制了相应的物理模型材料,并开展了大量力学加载试验研究,进而获得了材料的相关力学参数[33-34]。鉴于此,本次模拟选择该物理模型材料作为目标围岩,模拟过程中涉及到围岩的力学参数主要包括弹性模量、泊松比、抗压强度和抗拉强度。分析材料的岩石单轴压缩试验应力-应变曲线如图1所示。单轴抗压强度σc选取轴向应力应变曲线的峰值,即σc=8.43 MPa;弹性模量E选取σc/2处轴向应力-应变曲线的斜率,即E=2.5 GPa;泊松比μ选取σc/2处径向应变与轴向应变的比值,即μ=0.21。此外,由劈裂试验得到材料的抗拉强度σt=0.75 MPa。物理模型材料的制作及力学加载试验结果详见文献[33]。

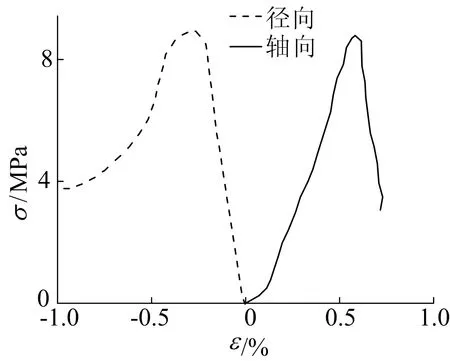
图1 模型材料单轴压缩应力-应变曲线

用上述物理模型材料制作尺寸为800 mm×800 mm×200 mm(长×宽×厚)、中心φ160 mm的钻孔物理模型试件,并在中国科学院武汉岩土力学研究所大型真三轴模型试验机上开展平面应变模型试验,如图2所示。在钻孔模型试件四周(即图2中试件上下左右4个面)施加相同大小的荷载,以模拟地下均匀应力场。试验荷载从2.50 MPa开始加载,以0.18 MPa/min的速度增加,从而模拟竖直钻孔钻进过程中随天然应力增加条件下围岩的破坏过程。在整个试验加载过程中对模型孔壁进行内窥摄影观测。物理模型试验流程参见文献[33-34]。

图2 钻孔模型试件及真三轴试验机

1.2 试验过程及结果

试验过程的钻孔内窥摄影照片如图3所示。由图3可知:当试验应力加载到3.88 MPa时,孔壁左上角出现肉眼可见的微小裂纹,这表明围岩进入塑性状态,产生了塑性变形;在3.94 MPa时,孔壁裂纹迅速扩展,贯通到整个孔壁,且伴随着一定的碎片剥离;之后的一段应力范围内,围岩未表现出新的破坏特征,破坏过程出现相对稳定期;然而当应力加载至4.44 MPa时,围岩突发显著破坏,裂纹快速扩张,孔壁大范围内出现碎屑和碎块的崩塌、垮落;之后应力加载至4.88 MPa的过程中,围岩未发生明显破坏,破坏过程再次进入相对稳定期。

图3 不同应力下模型试验钻孔壁破坏内窥摄影照片

2 数值模拟

2.1 模型建立

根据图1的物理模型材料室内单轴试验应力-应变曲线,应力达到峰值后,模型材料承载能力迅速降低。这表明随着塑性应变的增加,模型材料将发生显著的应变软化效应。因此可选取FLAC3D中的应变软化模型模拟钻孔围岩的破坏过程。该模型是基于与剪切流动法则不相关联而与拉力流动法则相关联的MohrCoulomb模型,围岩塑性屈服后,黏聚力c、内摩擦角φ、剪胀角γ

和抗拉强度σt发生弱化[35]。

为得到相关计算参数,首先通过数值试验确定模型材料强度参数随塑性应变弱化的线性关系。基于室内试验基本参数,采用应变软化模型进行单轴压缩数值试验,得到了与室内单轴试验应力-应变曲线相似性较高的数值试验曲线。选取此时的强度参数c、φ、γ与剪切软化参数εps、σt与拉伸软化参数εpt的关系作为数值模型的计算参数[36],如图4所示。

由图4可知,当塑性应变超过0.1,围岩强度便下降为残余强度值。

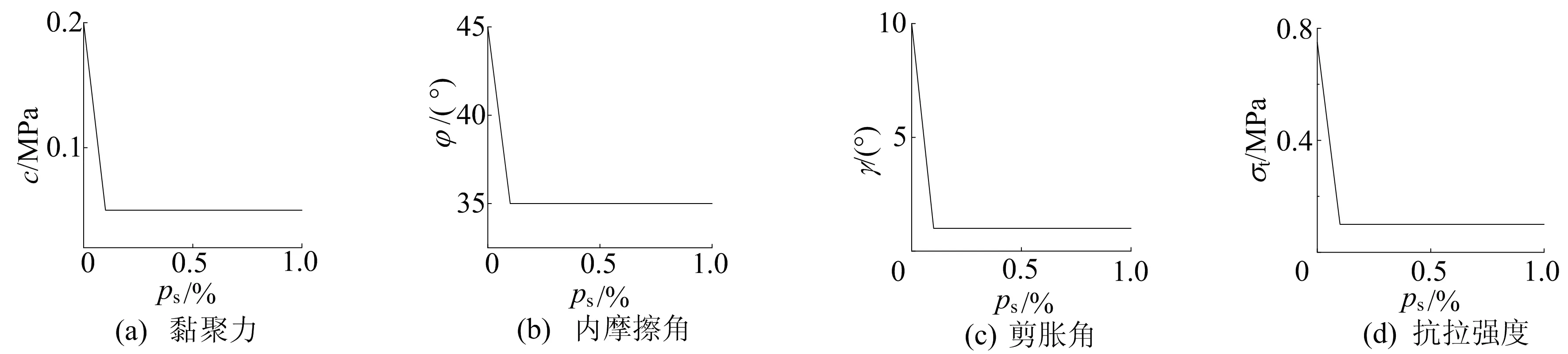
图4 应变软化模型计算参数

数值模型的几何尺寸、边界条件及加载条件与物理模型试验一致,模型及网格划分如图5所示。

图5 数值模型及其网格划分

2.2 模拟结果

模拟得到应力增加过程中钻孔围岩单元塑性区的发展过程如图6所示。

从图6可以看出：应力为3.88 MPa时,围岩已进入塑性状态,孔壁周围出现较小范围塑性区,结合物理模型试验过程中围岩的破坏特征,这一阶段可称之为塑性变形初始阶段;应力从3.88 MPa到3.94 MPa的低幅度增加过程中,围岩单元的塑性区扩展较快,范围明显增加,称之为塑性变形敏感阶段;此后应力到4.38 MPa的过程中,塑性区发展缓慢,变化不大,称之为塑性变形稳定阶段;当应力达到4.44 MPa时,围岩塑性区再次迅速扩展,范围显著增大,具有明显的突发性,称之为塑性变形突发阶段;而后应力增加过程中,塑性区发展却表现为速度减缓,增大不明显,可称之为塑性变形后期缓增阶段。

从图6的模拟结果可以看出,钻孔围岩单元主要处于shear-p(过去剪切)和shear-n(现在剪切)状态,因此剪切破坏是钻孔围岩的主要破坏形式。

图6 数值模拟围岩单元塑性区发展过程

数值模拟得到的各应力下围岩单元塑性区体积变化如图7所示。

由图7中各段折线斜率可看出,围岩单元塑性区体积的变化并不是随应力增加而线性增加的。

塑性变形初始阶段(应力为3.88 MPa),围岩开始出现塑性区;塑性变形敏感阶段(应力为3.94 MPa),塑性区体积在较短应力增幅内增长较快;塑性变形稳定阶段(应力为4.38 MPa),塑性区体积在较长应力范围内增长较缓;塑性变形突发阶段(应力为4.44 MPa),塑性区体积在较短应力增幅内迅速增加;塑性变形后期缓增阶段(应力为4.88 MPa),塑性区体积在较长应力范围内增长缓慢。

图7 数值模拟围岩单元塑性区体积变化

由图4可知,当围岩塑性应变大于0.1,其强度下降为残余强度值,这一区域称之为残余区[5-24]。模拟可进一步得到应力增加过程中,钻孔围岩单元残余区的发展过程,如图8所示。

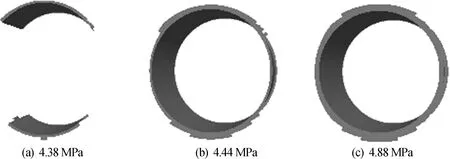
图8 数值模拟围岩单元残余区发展过程

在经历较长的塑性变形发展后,围岩在塑性变形稳定阶段后(应力为4.38 MPa)开始出现未连通的残余区;并且在塑性变形突发阶段(应力为4.44 MPa),残余区迅速扩展贯通,且范围明显增加;在之后较长的塑性变形后期缓增阶段(应力为4.88 MPa)，围岩残余区发展缓慢,变化并不明显。

2.3 模拟结果对比及分析

采取围岩应变软化模型得到的数值模拟结果,清晰地展现了钻孔围岩塑性区、残余区的发展变化过程,从塑性应变的角度定量地表现了钻孔围岩的破坏过程,较好地对应了物理模型试验中定性描述的围岩破坏过程。

从图3可以看出,物理模型试验中,应力达到4.44 MPa时,围岩较大范围出现碎屑和碎块,破坏程度突增,但在其他应力过程中,围岩整体的破坏程度变化并不是很明显。在围岩塑性区中,残余区的塑性应变最大,其破坏程度也最大,因此可以从围岩残余区的发展过程来解释这一现象。试验前期围岩残余区未出现或范围较小,故围岩整体破坏不明显;但应力达到4.44 MPa时,残余区迅速扩展,故围岩破坏程度显著增大;之后的过程中残余区变化较小,围岩未发生明显破坏。

对数值和物理模拟中钻孔围岩的破坏过程进行分析可知，开始施加荷载后,孔壁的应力集中最大,但在较低应力状态下,整体呈现弹性状态;当应力加载至3.88 MPa时,孔壁处的应力超过了围岩屈服极限,围岩进入塑性状态,开始产生塑性变形,塑性区开始发育,孔壁出现微小裂纹;随着应力持续增大,塑性变形和塑性区范围不断增加,孔壁的破坏程度和范围也持续增大。

根据图1,该材料在应变达到一定值时承载力明显下降,即抵抗变形的能力下降,因此围岩的变形不仅与应力有关,还受先前的应变所制约。围岩的变形和破坏不仅仅是简单地随应力增加而加剧,而是当应力超过一定阈值后,其变形和破坏可能表现出一定的突发性和稳定性。

当应力为3.94 MPa时,由于先前加载过程中积累的应变,较小范围内围岩的承载能力迅速下降,塑性区范围迅速增加,孔壁裂纹迅速扩展贯通;当应力达到4.44 MPa时,更大范围的围岩承载能力迅速下降或下降到更低水平(即残余区范围显著增加),故而塑性区范围和围岩的破坏程度都表现为突发性增大。在以上2次围岩发生显著破坏后的一段应力过程中,围岩承载力下降不大,同时围岩应力也得到了调整和释放,故围岩变形破坏特征不明显。

3 工程实例验证分析

青东矿位于安徽省淮北市濉溪县。该矿839工作面位于三采区东部,近年来开展了大量的补勘工程。为了探究补勘钻孔围岩破坏情况,采用钻孔彩色电视对839工作面典型补勘钻孔进行了观测,收集到部分埋深及对应的原位地应力处砂岩钻孔照片,如图9所示。

图9 砂岩钻孔电视照片

从图9可以明显地看出:埋深280 m处(应力8.7 MPa),岩石原生裂隙发育,完整性一般;从埋深331 m处开始(应力10.7 MPa),在原生裂隙的基础上,少数孔壁裂隙得到了扩展、贯通,对应模拟中的塑性变形初始阶段;之后一段埋深内孔壁裂隙继续发育、贯通,在埋深377 m处(应力12.4 MPa)孔壁出现多条贯通的裂隙,对应模拟中的塑性变形敏感阶段;在埋深389 m处(应力12.9 MPa),孔壁破坏情况与377 m处相近,对应模拟中的塑性变形稳定阶段;在埋深413 m处,此时应力高达13.8 MPa,钻孔围岩出现严重破坏,被分裂成较大、较多的碎块,部分崩落后孔壁出现较大缝隙,对应模拟中的塑性变形突发阶段。

由于钻孔观测深度的限制,本研究未能进一步观看到围岩塑性变形后期缓增阶段的钻孔电视照片。

根据钻孔围岩的破坏程度及围岩的稳定性,可以把其破坏过程分为2个部分、埋深389 m之前,围岩裂隙逐渐发育贯通,围岩破坏程度较小,且过程相对稳定,对围岩稳定性影响较小;在389 m之后的有限埋深范围内,孔壁周围的围岩被显著分裂,破坏严重,表现出一定的突发性破坏特征,钻孔的围岩稳定性大幅下降。

综上所述,由工程实例观测得到的钻孔围岩破坏过程及其特征与数值和物理模拟研究结果相一致。