VDW在框架结构中的减震性能分析及工程应用

王扬帆, 陈道政，2

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.中国地震局工程力学研究所 地震工程与工程振动重点实验室,黑龙江 哈尔滨 150080)

地震发生时,地面的振动引起建筑物产生相应的地震反应,当建筑物某些结构部分(如梁、柱等)的地震反应超过一定限值时就会引起结构部件的严重破坏,甚至失效倒塌,因此现代结构物的消能减震技术愈发受到人们的重视。黏滞阻尼墙(viscous damping wall,VDW),是一种安装在结构层间的墙式减震装置,属于被动控制减震部件。它能在不影响原结构周期振型的前提下,通过高分子黏滞材料产生阻尼力来耗散地震作用或风振作用下输入结构的大部分能量,具有良好的消能减震效果。相比于传统的消能装置,VDW具有以下特点:① VDW黏滞材料接触面积大,提供阻尼力效果更可观;② 安装及后期维修保养费用低,且材料简单,施工误差对VDW减震性能影响较小;③ 布置更加灵活,可设置在墙体中,不影响建筑美观,达到“隐形”的效果;④ 适用范围广,在框架、框剪及多高层结构中均可以使用[1]。本文通过在一栋框架结构中设置普通杆式阻尼器及VDW,来对比分析VDW在多种地震情况下的反应,探索总结VDW的实际耗能减震效果,为后续关于VDW布置、模拟设计及减震效果分析提供参考。

1 VDW减震原理

VDW装置构造主要由黏滞体容器(外钢板)、阻力板(内钢板)、黏滞体(高分子黏滞液体材料)3个部分组成[2],根据阻力板的数量又分为单层型和双层型阻尼墙,如图1所示。

图1 VDW构造图

VDW主要通过楼层间的相对水平位移来产生阻尼力,属于速度相关型消能器,其工作原理如图2所示。

图2 VDW工作原理

外钢板组成黏滞体容器,固定于楼层下部梁顶面,内钢板嵌固在楼层上部梁底并置于填满黏滞性液体的容器中,在地震作用或者风振作用使结构产生侧层间位移时,内、外钢板在黏滞液体中产生相对位移从而产生黏滞阻尼力,以此来部分抵消输入结构的外部能量。VDW由于内、外钢板并没有直接接触,因此本身不存在可以计算的刚度,减震作用主要是依靠阻尼提供。

2 VDW力学模型及计算公式

VDW往往采用精确的Maxwell计算模型[3],这与SAP2000软件中Damper黏滞阻尼单元[4]采用的计算模型相同,该模型是由1个阻尼器单元与线性弹簧单元串联而成,如图3所示。

图3 阻尼单元示意图

假设阻尼器与线性弹簧单元的位移分别为uc及uk,其力学计算公式如下:

u=uc+uk

(1)

fd=kuk=cvcα

(2)

其中:fd为VDW产生的抵抗力;k为弹簧常数;c为阻尼系数;α为速度指数;vc为阻尼器变形速度。

3 工程概况及布置方案

3.1 工程概况

六安市某便民服务中心纯框架结构,底层层高4.2 m,其余层层高3.6 m,建筑总高度为25.8 m,共7层。柱混凝土采用C35混凝土,梁、板混凝土采用C30混凝土,受力钢筋及箍筋均采用HRB400级钢筋。底层柱、二至五层柱、六至七层柱截面尺寸(宽×高)分别为600 mm×600 mm、500 mm×500 mm、400 mm×400 mm,主梁尺寸为300 mm×600 mm,次梁尺寸为250 mm×500 mm及200 mm×500 mm,板厚100 mm。该工程抗震设防烈度为7度(0.10g),丙类抗震设防,设计地震分组第一组,Ⅱ类场地,场地土特征周期为0.4 s。现拟采用普通杆式阻尼器和VDW 2种不同方案进行加固设计。

3.2 布置方案

结构底层平面布置图如图4所示(单位为mm)。

结构的减震耗能效果与VDW的布置位置有很大关系,一般需要将阻尼墙布置在层间位移较大及楼层加速度较大的部位。经对原结构建模分析发现,结构在底层及顶层的层间位移较小,且楼层越高楼层加速度反应越明显。考虑建筑物房间用途以及尽量减少对开窗部位的影响,拟在二至六层布置阻尼墙,其中每层Y方向分别在① 轴、⑧ 轴上的B～C轴之间及D～E轴之间布置阻尼墙,X方向分别在B轴、E轴上的② ～③ 轴之间及⑥ ～⑦ 轴之间布置阻尼墙。为对比杆式阻尼器与阻尼墙减震效果,杆式阻尼器布置位置同VDW布置方案。

3.3 阻尼器参数选取

普通杆式阻尼器参数见表1所列,VDW参数见表2所列。

表1 普通杆式阻尼器参数

表2 VDW参数

4 有限元模型的建立与分析

4.1 阻尼器模拟原则

在现有的SAP2000软件中并没有VDW连接单元,但前述提及阻尼墙常用计算模型与SAP2000中的Damper杆单元计算模型相同,因此可以设法利用Damper杆单元连接来模拟VDW工作模式[5]。实际上,VDW利用层间相对水平位移以面剪切的方式产生阻尼力进行耗能,而且在实际工程中,VDW的设计也仅考虑阻尼墙水平方向的阻尼力,忽略竖向位移产生的阻尼力,故可以采用在楼层上、下梁中间布置多个竖向Damper连接单元的方法来近似模拟VDW的面剪切工作原理。在本工程中,采用3个竖向Damper连接单元进行VDW模拟,由于主要考虑水平方向层间位移影响,故需设定其U2、U3方向非线性[6],单个Damper阻尼器内部刚度为(200/3)MN/m,阻尼系数为500 kN/(mα·s-α),VDW立面示意图与模拟图如图5所示。

图5 VDW立面示意图与模拟图

普通杆式阻尼器同样采用Damper连接单元模拟,但其主要是靠杆中轴力作用于阻尼器上产生阻尼力,故须设置其沿杆端方向非线性,阻尼系数为800 kN/(mα·s-α)。

4.2 模型建立与地震波的选取

为对比VDW减震效果,拟根据条件建立3个方案模型。方案1为原框架结构模型,方案2为增设普通杆式阻尼器后的框架模型,方案3为增设VDW后的框架模型。有限元模型通过SAP2000软件建立,采用线单元定义框架梁、柱,采用壳-薄壳单元定义楼板并忽略横向剪切,并赋予结构荷载及各种分析下的工况[4]。3个方案下的SAP2000模型如图6所示。

图6 3个方案下的SAP2000模型

采用时程分析法时,为了考虑地震波的随机性,应按建筑场地类别和设计地震分组选用实际强震记录和人工模拟的加速度时程曲线,其中实际强震记录的数量不应少于总数的 2/3[7]。根据本工程场地土及地震信息等条件,拟采用El Centro天然地震波、Tangshan SN天然地震波以及上海人工波作为地震波能量输入,3条地震波原加速度峰值分别为341.70、55.49、35.00 cm/s2,需调整比例系数来控制时程函数整个时间范围内的函数值大小,以满足抗震规范所规定加速度有效峰值的要求。3种地震波时程曲线如图7所示。

图7 3种地震波时程曲线

4.3 模态分析

对3个方案中的模型进行模态分析,结果显示,在不考虑杆式阻尼器与VDW的自重因素前提下,方案2、方案3中结构周期振型与方案1相同。这表明普通杆式阻尼器与VDW均具有“静刚度”的特点,即在静力线性分析时支撑不体现刚度作用,不影响原结构的周期及振型。模态分析结果见表3所列。

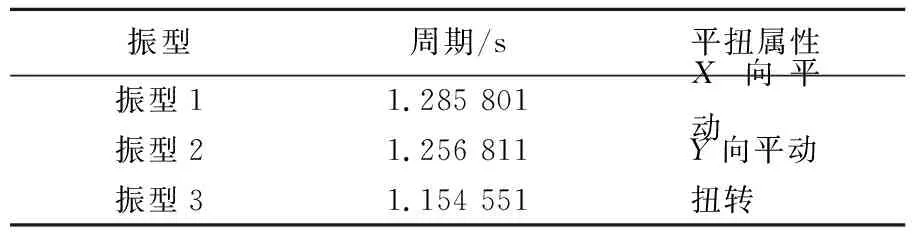
表3 结构前3个振型周期特点

4.4 反应谱分析

SAP2000软件对于反应谱分析方法,给出了多种组合方法,为更接近于实际工程情况且考虑阻尼引起的振型间的静态耦合效应,本文采用以随机振动理论为基础的完全平方根组合(complete quadratic combination,CQC)方法[4]。3个方案反应谱分析下的层间位移角如图8所示。

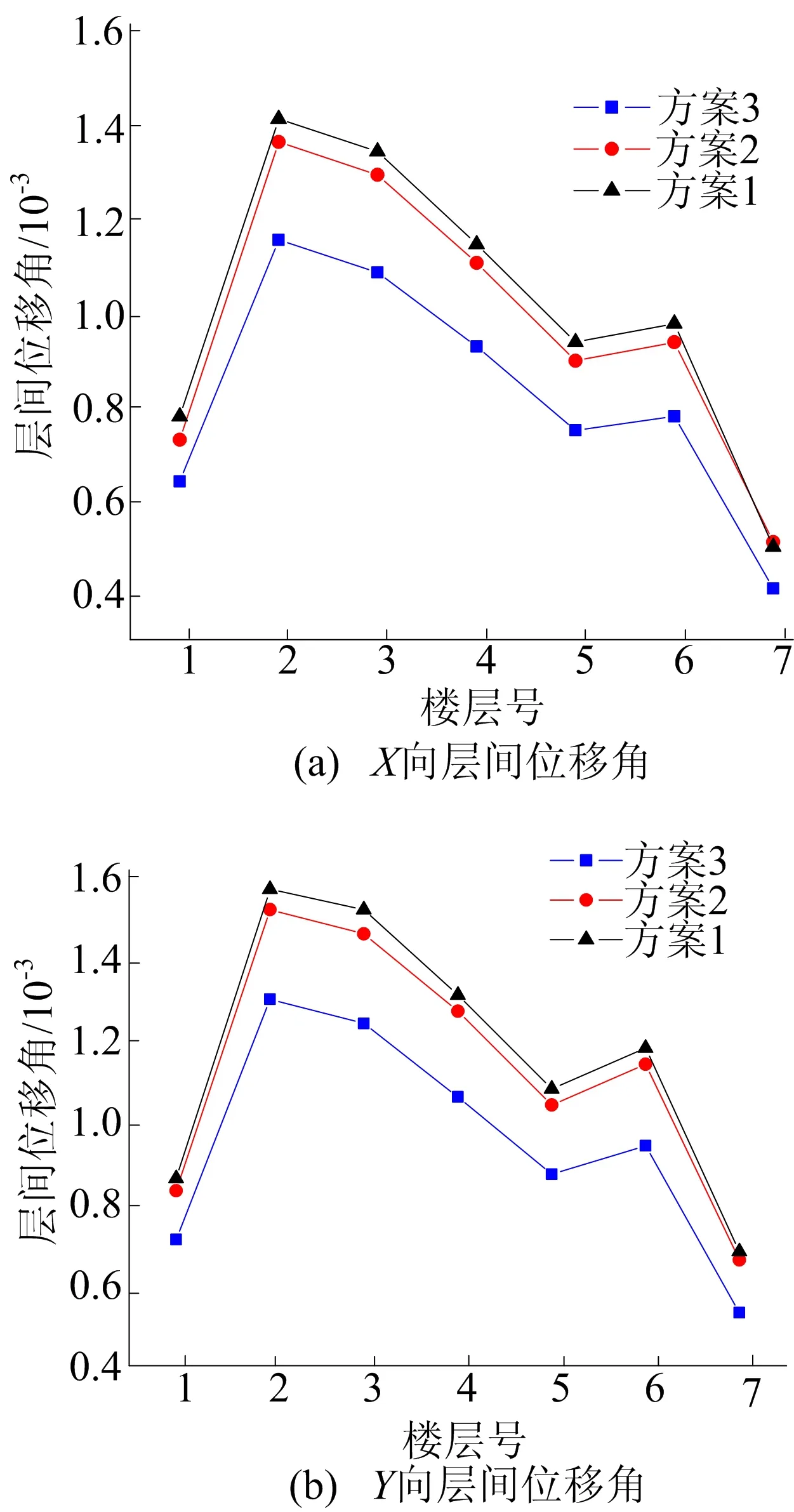
图8 3个方案反应谱下位移响应

由图8可知:① 在反应谱分析下,3个模型在Y方向的层间位移角普遍都比X方向的大,且在第2层、第6层层间位移角产生突变,这主要与原框架结构布置形式有关,原结构Y向刚度要远小于X向刚度,且在第2层、第6层处柱截面发生了变化,因此竖向构件的抗侧刚度发生较大变化,产生较大层间相对位移;② 方案2及方案3的层间位移角比方案1均有所降低,但明显方案3降低的幅度更大,减缓位移反应效果更明显,其最大层间位移角(第2层)从1/636降到1/769,降幅达17%,这说明普通杆式阻尼器在拟动力分析下减震效果并不是很明显,而增加VDW虽然不能增加结构的刚度,但可以通过黏滞材料产生黏滞阻尼力来达到减小振动反应的目的。

4.5 多遇地震下位移及加速度响应

3个方案在不同波形、峰值地震波下的最大加速度amax及其平均降幅、最大位移等信息见表4所列。

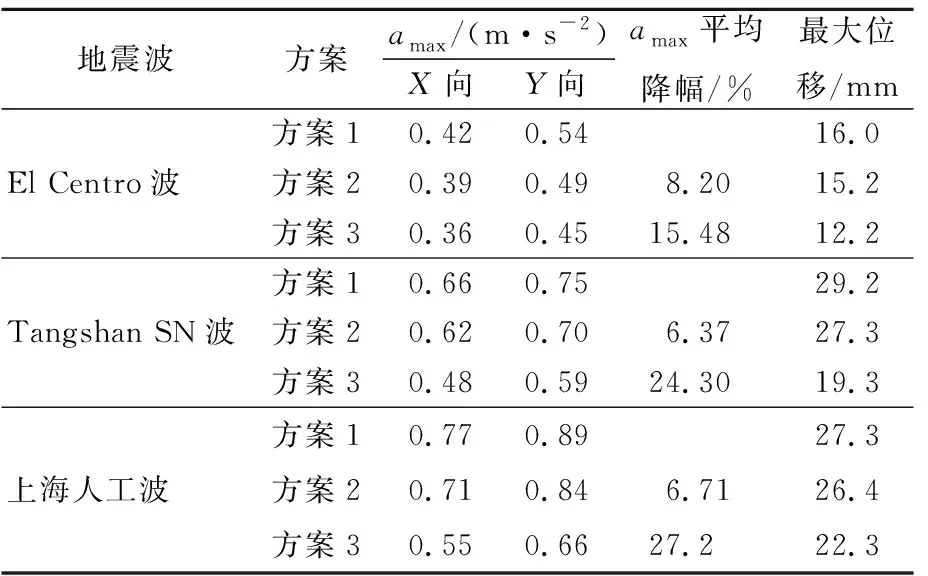
表4 结构在3种地震波下的加速度、位移响应

在地震或者风振等水平力作用于建筑物上时, 结构会发生振动响应[6],当振动响应过大时在其中活动的人就会产生不舒适的感觉而引起恐慌不安心理,这种情况在多、高层结构中尤为常见,因此舒适度分析也是结构性能好坏的重要评价指标,而结构最大加速度又是舒适度分析的关键衡量因素。

由表4可知:① 布置普通杆式阻尼器及VDW的结构,其最大加速度及最大位移均得到了有效控制,结构Y向加速度略大于X向加速度,位移变化均低于文献[7]的层间位移角限值(1/550),特别在Tangshan SN波下方案3最大位移从方案1的29.2 mm降至19.3 mm,控制结构位移反应的效果显著; ② 方案2最大加速度平均降幅在6.37%～8.20%之间,方案3最大加速度平均降幅在15.48%～27.21%之间,相比之下VDW减震降速效果更为理想;③ 方案3结果还表明,在峰值加速度不同、波形不同的地震激励下,VDW对加速度及位移减小的效果存在一定的差异,这主要与不同地震波下VDW阻尼器变形速率有关(速度型阻尼器特点),地震波峰值变化越快,引发楼层剪切变形速率越大,消能器产生的阻尼力也越大。

在小震的情况下,杆式阻尼器及VDW作用位移及相对运动速度均较小,但是相同激励条件下VDW的阻尼板移动所能提供的剪切面积更为可观,故VDW在小位移时产生大阻尼力,能更有效地降低楼层加速度和位移。

4.6 罕遇地震作用下的时程分析

4.6.1 各地震波下位移响应

输入3种不同波形并调整峰值加速度的地震波作为激励后,结构的层间位移角变化趋势如图9所示。

由图9可知:在罕遇地震下方案2、方案3均能控制改善框架结构的位移反应,但总体上VDW结构在大震中的减震效果更佳;在各地震波下,最大层间位移角仍出现在第2层,也即柱变截面刚度变化处。

结构总位移及最大层间位移角见表5所列。

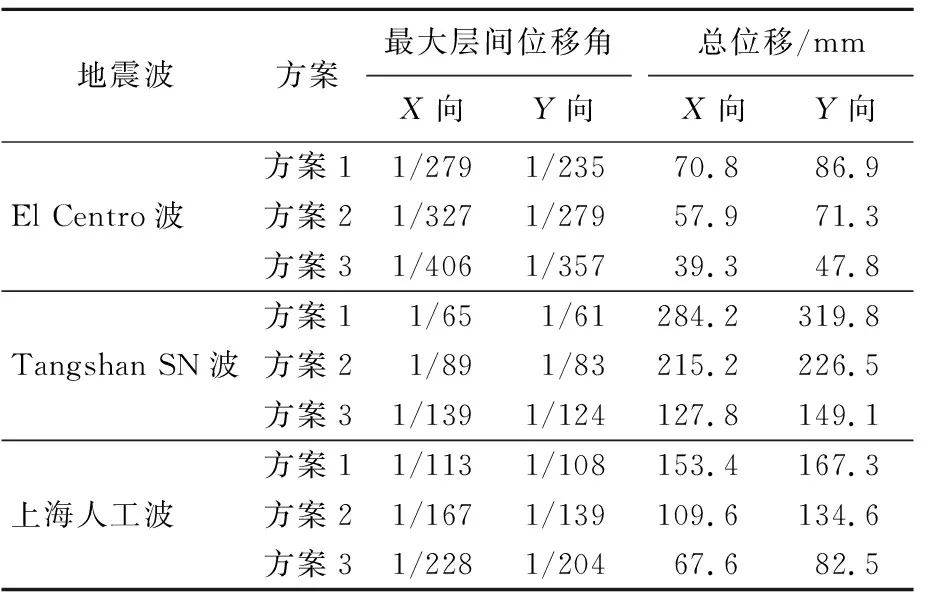
表5 3个方案下的最大层间位移角、总位移

由表5可知:方案1在El Centro波、Tangshan SN波、上海人工波下层间位移角最大值分别为1/235、1/61、1/108,尤其在Tangshan SN波下接近于罕遇地震下弹塑性层间位移角的国家规范限值(1/50)[7],结构抗震安全储备不是十分充足;但增加杆式阻尼器后,结构最大层间位移角在各地震波下分别降至1/279、1/83、1/139,分别为原结构位移角(方案1)的84.20%、73.5%、77.7%,而增加VDW后,结构最大层间位移角在各地震波下分别降至1/357、1/124、1/204,分别为原结构位移角(方案1)的65.8%、49.2%、52.9%。由此可见,VDW结构在大震下控制薄弱层变形方面效果突出,最大可以实现50%左右的层间位移降幅,这也与VDW结构在大位移、高加速度情况下能提供更大阻尼力密切相关。

由图9、表5可知:加普通杆式阻尼器后各楼层层间位移角比原结构降幅在14%～35%之间,在3种地震波下总位移分别为71.3、226.5、134.6 mm,为方案1总位移的82.0%、70.8%、80.5%;增加VDW后,各层间位移角比原结构降幅在26%～64%之间,在3种地震波下总位移分别为47.8、149.1、82.5 mm,为方案1总位移的55.0%、46.6%、49.3%。从整体层间位移变化趋势可以看出,大震时VDW在其他层位移的控制改善上也有显著效果,在不同峰值及波形的地震波下可基本达到50%左右的位移控制效果,杆式阻尼器所提供的阻尼效果不如VDW结构的阻尼效果可观。

罕遇El Centro波下方案3与方案1相比，层间位移角降幅比例见表6所列(经计算,罕遇Tangshan SN波及上海人工波下变化趋势同El Centro波下情况,这里不再列出)。各楼层层间位移角降幅比例为:(方案1数值-方案3数值)/方案1数值。

表6 罕遇El Centro波下层间位移角降幅比例 单位:%

VDW降低楼层位移能力与其所布置楼层的高度呈正比例的关系,布置VDW的楼层越高(底层及第7层未设置VDW),其降低楼层位移的能力越强,这也恰恰体现了阻尼器作为速度型耗能构件的特性。因为楼层越高,其瞬时速度及加速度等地震响应越大,而VDW阻尼力与阻尼器速度呈正相关,所以随楼层号增加,产生的阻尼力也递增。

4.6.2 加速度响应及层间剪力响应

3个方案在罕遇地震下的最大加速度(amax)及基底剪力(Fs)见表7所列。与多遇地震下的加速度反应相同,在大震的情况下最大加速度仍出现在第7层。

3种地震波下层间剪力变化如图10所示。

由表7可知:方案2、方案3均有效降低了楼层加速度以及基底剪力,很好地发挥了杆式阻尼器和VDW的耗能减震作用;其中方案3中的最大加速度要远小于方案2及方案1,在不同波形、峰值的地震波下方案3相对于原结构最大加速度减少了31.8%～48.6%,方案2相对于原结构减少了17.4%～27.5%,说明VDW在大震中更能有效降低混凝土框架结构的加速度反应,吸收耗散更多的地震能量;增加杆式阻尼器后的结构,基底剪力比原结构下降23.4%～27.8%,而增加VDW后结构基底剪力降幅能达34.7%～50.8%。

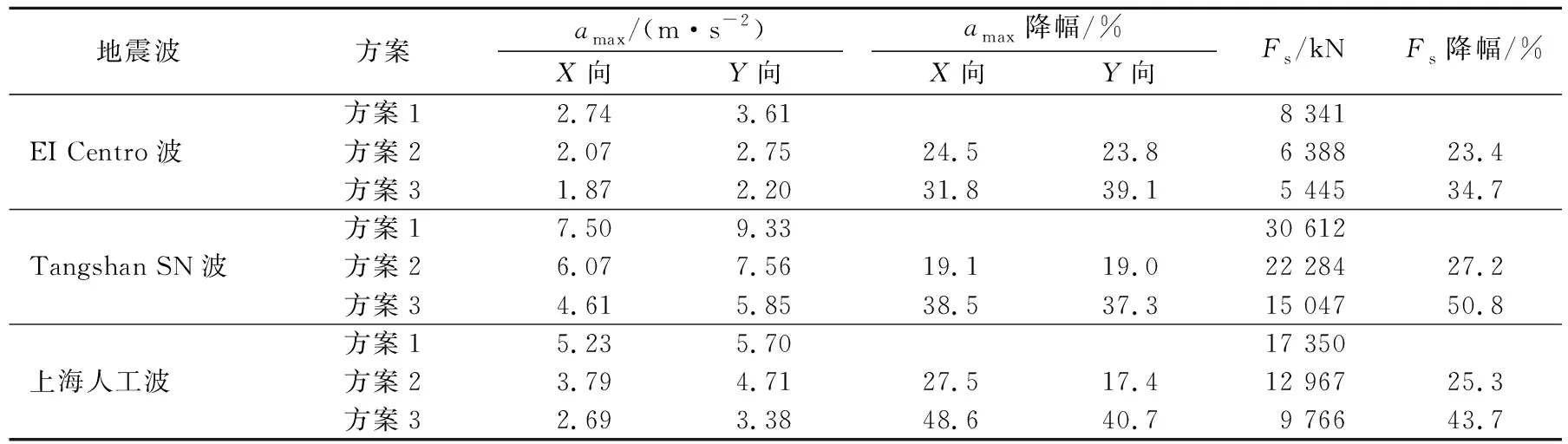
表7 3个方案下的加速度与基底剪力

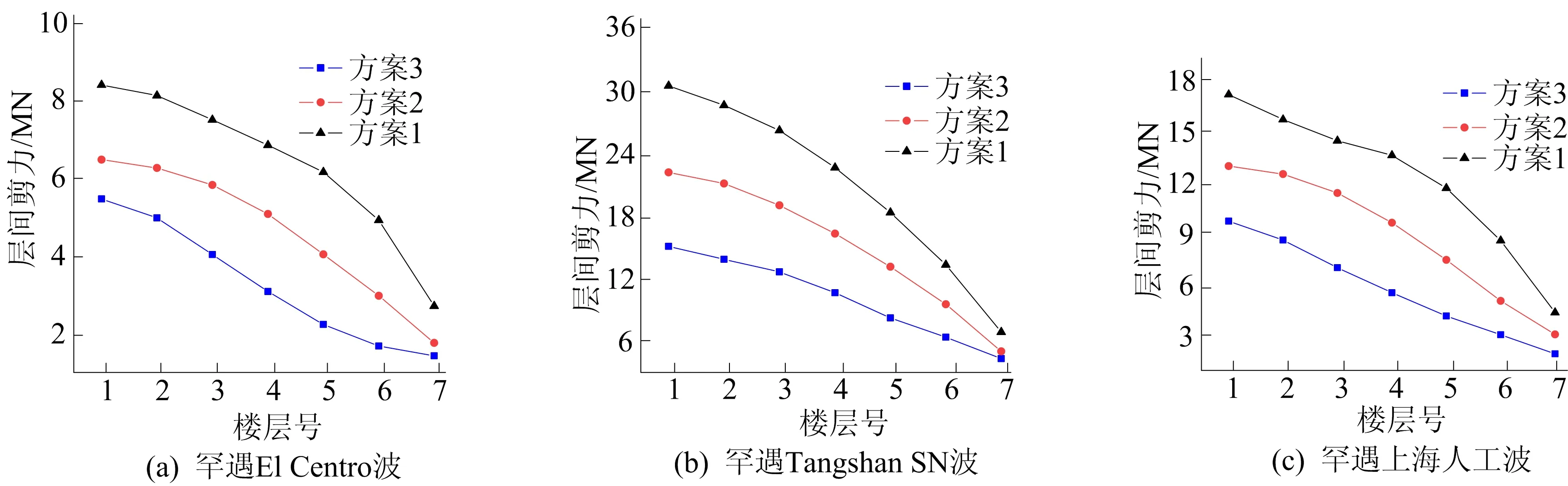
图10 3种地震波下层间剪力变化

由图10可知,3个方案按层间剪力从小到大排序依次为方案3、方案2、方案1。从图10可以看出,设置在高楼层的VDW减少层间剪力的幅度更大,达到30%～50%,在同样的地震波下VDW相较于普通杆式阻尼器结构能提供更大阻力面积,可以吸收耗散更多输入结构的地震能量,从而保护框架柱等主要构件,大大降低柱的剪力,达到大震不倒及强柱弱梁的目的。

4.6.3 地震能量耗散及滞回曲线

罕遇上海人工波下方案2、方案3结构能量耗散情况如图11所示。

罕遇地震下地震波输入结构的地震能量极大,结构会产生大位移、高加速度等地震响应[8]。从图11可以看出,VDW在这种大位移、高加速度的情况下能够产生更可观的阻尼力来抵消地震能量。地震传入结构的95%以上能量都被结构自身振动耗能和连接阻尼器构件耗能所抵消,在理想状况下(不考虑杆式阻尼器及VDW行程破坏的情况),同数量、同位置布置的普通杆式阻尼器仅能耗散抵消15%左右的地震能量,VDW构件则能耗散抵消40%左右的地震能量。由图11可知,VDW耗能能力在大震下远大于普通杆式阻尼器,能更好地保护主体结构的安全,防止主体结构承受过多地震能量而过早出现严重破坏。

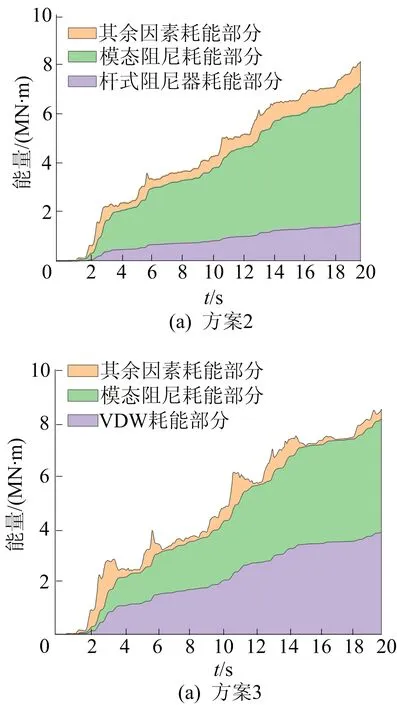
图11 罕遇上海人工波时2个方案下结构能量耗散情形

结构在地震作用下的耗能能力与滞回曲线的形状及面积密切相关[9],一般认为构件耗散抵抗地震作用的大小与滞回曲线的面积和滞回环的饱满程度呈正相关。方案2、方案3在Tangshan SN波下同一位置处杆式阻尼器与VDW的滞回曲线如图12所示。

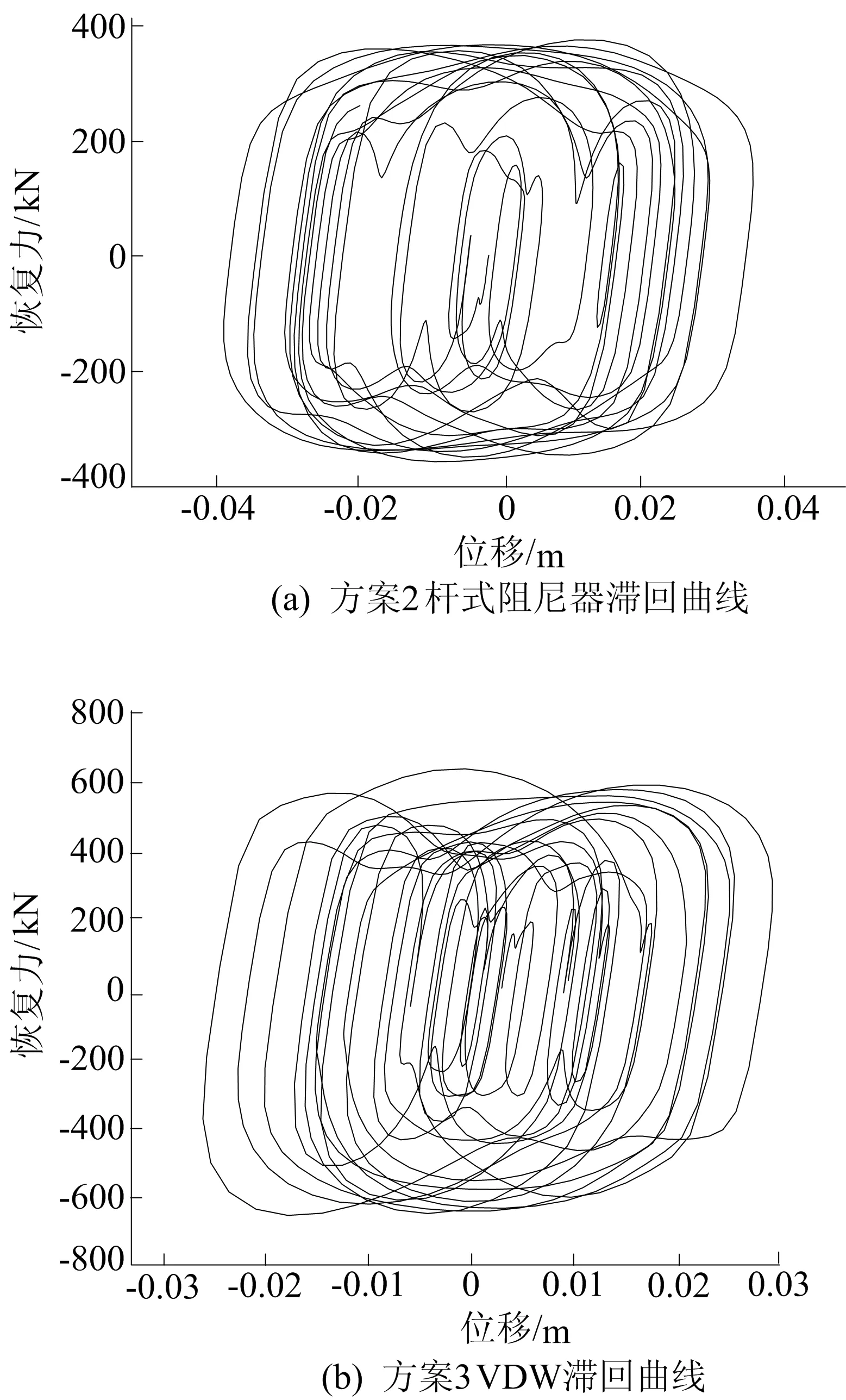
图12 Tangshan SN波下2个方案的结构滞回曲线

由图12可知:方案2耗能单元的最大恢复力为374.15 kN,方案3耗能单元的最大恢复力为632.78 kN,接近于方案2的1.7倍;方案2、方案3滞回曲线均呈现近似斜椭圆曲线,这也证明阻尼减震结构有在动力作用下产生“刚度”的特点;VDW结构的滞回曲线面积明显比杆式阻尼器结构面积大,耗能能力强于杆式阻尼器,且在小位移的情况下VDW结构明显比杆式阻尼器结构的滞回曲线更加饱满,这也验证了在小位移的情况下杆式阻尼器的减震耗能效果不明显,而VDW在大位移、小位移下均能保持良好的耗能能力。

5 结 论

本文通过分析对比设置杆式阻尼器和VDW后结构的消能减震效果,得到以下结论:

(1) VDW的减震耗能效果与布置位置和形式有关,一般需要结合建筑及房屋用途,将阻尼墙布置在层间位移或剪切变形速度较大的地方,并尽量避免对开窗的影响。

(2) 根据VDW工作原理与实际情况中仅考虑阻尼墙水平方向的阻尼力而忽略竖向位移产生的阻尼力的特点,可以采用多个竖向Damper阻尼器模拟VDW工作模式。

(3) 杆式阻尼器与VDW结构均体现出静刚度特点,在静力时几乎不体现刚度作用,主要依靠阻尼力来耗能减震。在小震作用下,杆式阻尼器结构所能提供的阻尼力比VDW结构要小,减震效果较弱;在大震时,杆式阻尼器结构与VDW结构均能很好地控制框架结构的地震反应,但VDW吸收耗散地震力的能力更显著,特别是VDW结构在大震下控制薄弱层变形方面效果突出,最大可以实现50%左右的层间位移降幅,最大加速度相对于原结构降低了31.8%～48.6%,层间剪力降幅能达到30%～50%。