一种新型非对称摩擦阻尼器力学性能研究

2022-03-05李梦如袁苗苗朱华年卢文胜

合肥工业大学学报（自然科学版） 2022年2期

方鑫, 李梦如, 袁苗苗, 朱华年, 卢文胜

(1.同济大学土木工程学院,上海 200092; 2.同济大学机械与能源工程学院,上海 201804)

结构抗震的传统方法在于提升结构本身的强度和变形能力,但由于地震与风作用及结构特征的不确定性,仅考虑提升结构抵抗力和变形能力可能并不经济,而通过增加结构阻尼以耗散地震与风作用能量、减小结构的响应和破坏是更合理的技术方向。近几十年来,结构抗震抗风研究发展中,许多减震(振)耗能技术被研发并应用于结构工程[1-3],其中阻尼器是一类非常有效的减震(振)元件,根据不同的阻尼机制耗散所输入的能量,从而有效降低结构在地震及风作用下的反应。

黏滞阻尼器、摩擦阻尼器及金属阻尼器等常见的阻尼器[4]在外力或者位移作用下常保持力学性能的对称性。因此,文献[5]尝试将阻尼器有效地应用于某些双向异性构件;文献[6]研发了非对称黏滞阻尼器，并对其进行力学性能试验及分析;文献[7]提出以耗能钢片与释压装置组成的无压力支撑系统,在钢框架试验中展现了良好的耗能与恢复性;文献[8-9]提出一种仅提供拉力的金属屈服耗能装置用于摇摆墙和支撑等构件,并对该装置进行性能试验及参数分析,表明可作为附加阻尼装置为系统提供更好的耗能能力。

考虑到柔性结构具有长周期、低速度和大位移等特征,本文研发一种新型非对称摩擦阻尼器,其受拉与受压2个方向力学性能不同,建立简化力学模型,并进行力学性能试验,验证了所提出的力学模型能较好地模拟其非对称力学性能。

1 新型非对称摩擦阻尼器力学模型

摩擦阻尼器一般通过滑动部件之间的摩擦将动能转化为热能来耗散能量[10]。作为一种类位移型阻尼器,摩擦阻尼器通常用非线性的力-位移模型来描述其力学性能[11],常见有刚塑性模型和弹塑性模型[12]。考虑将其应用于具有双向异性受力特征的构件(如柔性拉杆或支撑),其拉伸屈服与回缩屈曲或松弛性能不同,这就需要设法使该类型阻尼器的2个方向具有非对称性能,本文将其定义为“非对称摩擦阻尼器”,类似于机械工程中使用的单向减震器[13]。

新型非对称摩擦阻尼器是基于摩擦板间相对滑动的摩擦机理,但设置了具有非对称力学性能的构造而产生的。采用棘轮这一间歇性机构,可使阻尼器在一个方向运动时,棘轮能够传递运动,可产生阻尼力;而在相反方向运动时,棘轮空转无法传递运动,基本上不产生阻尼力,从而实现2个方向差异的力学性能。

基于经典库伦摩擦理论的纯摩擦机构的力学模型为理想刚塑性,而考虑实际非对称摩擦阻尼器中其他装置部件及连接件自身的附加刚度贡献,可用弹塑性模型表征其力学性能,即模型具有一定的初始刚度。2种阻尼器的滞回曲线如图1所示,其力学模型见表1所列。其中:F为阻尼力;Fmax、Fmin为摩擦阻尼力双向峰值;d(t)为阻尼器位移;弹塑性模型中kd为阻尼器弹性刚度;dy、dmax分别为弹性极限位移和峰值位移。由此可见,非对称摩擦阻尼器在2个方向上产生的摩擦阻尼力完全不同。

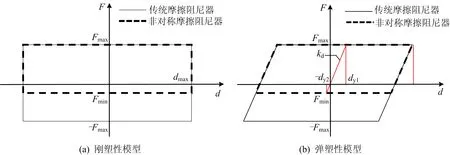
图1 2种摩擦阻尼器滞回曲线

表1 2种摩擦阻尼器力学模型

2 新型非对称摩擦阻尼器的设计制作

新型非对称摩擦阻尼器通过设置棘轮使阻尼器在摩擦板之间一向运动时棘轮卡死,产生稳定的摩擦力;而反向时则棘轮空转,摩擦片趋于不滑动,几乎不产生摩擦力。文献[8-9]提出的一种仅提供拉力的单向耗能装置采用直线设计,在行程中无法复位。而采用可旋转的单向棘轮与特定行程的摩擦片组合,可适应单向受力且可轻松复位的大变形需求,通过调节两侧高强度螺栓及预紧弹簧的预紧力可以改变摩擦板之间的正压力,从而获得双向不同的摩擦阻尼力。

设计制作的阻尼器示意图如图2所示,样品如图3所示,主要构件尺寸见表2所列,定义阻尼器两端产生相离位移时为正(即阻尼器受拉),产生相向位移时为负(即阻尼器受压)。在最大预紧力情况下,设计受拉方向峰值阻尼力最高可达30 kN,而受压方向峰值阻尼力接近于0。

图2 新型非对称摩擦阻尼器示意图

图3 新型非对称摩擦阻尼器样品

表2 阻尼器主要构件尺寸及材料单位:mm

3 新型非对称摩擦阻尼器性能试验

3.1 低周往复加载试验

为研究该阻尼器滞回性能,并验证上述提出的力学模型,对研制的非对称摩擦阻尼器样品进行相关力学性能试验。该阻尼器两端连接板分别与固定于地面的反力墩、作动器相连,在作动器与连接板的中间设置量程为100 kN的力传感器。试验装置如图4所示。

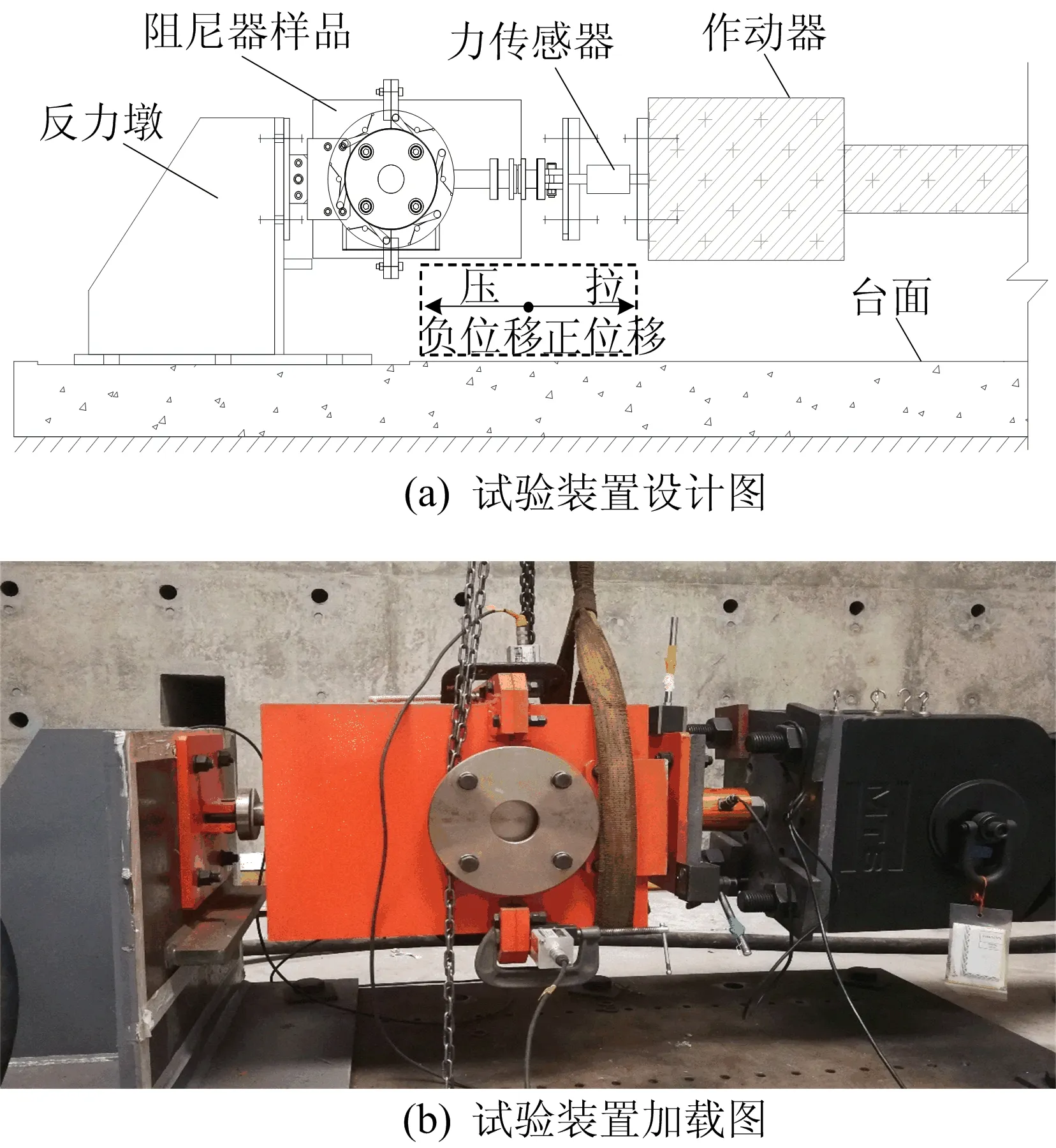
图4 非对称摩擦阻尼器性能试验

试验过程中采用位移控制的低周往复加载方案,位移按照正弦函数规律变化,具体如下:

d(t)=dsin(ωt)=|dmax|sin(2πft)

(1)

其中:f为频率;dmax为峰值位移。

加载时的力和位移数据通过相应传感器记录并由试验装置采集输出。

试验时,通过调节预紧弹簧的压缩量以改变摩擦板之间的预紧力,从而实现摩擦阻尼力的变化,同时改变阻尼器峰值位移,对阻尼器样品进行多组试验。

试验结果达到了预期的非对称力学性能。在所有工况中,非对称摩擦阻尼器整体上出力稳定,阻尼器受拉时稳定为正值,而受压时阻尼力几乎为0。每个工况进行3个循环,每个循环的滞回曲线中的阻尼力都比较平稳,3条曲线也比较接近。试验中可看出阻尼器带有一定的初始刚度,其滞回曲线非常饱满,表明其耗能性能良好。

3.2 试验结果分析

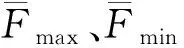
表3 非对称摩擦阻尼器性能试验结果

选取不同预紧力下典型工况的滞回曲线如图5所示。从图5可以看出,试验阻尼器在受拉时出力远远大于在受压时出力,Fmax最大值为22.0 kN,而Fmin约为-0.5 kN,且在相同预紧力、不同峰值位移时,Fmax都十分接近,说明峰值位移对峰值阻尼力的影响不大。在所有预紧力不为0的工况中,受拉峰值阻尼力均远远大于受压峰值阻尼力,验证了阻尼器的非对称性。

图5 典型工况的滞回曲线

试验结果表明,非对称阻尼器力学性能满足预期的需求。但在所有工况中,都会出现“空程”情况，即阻尼器位移到达负向峰值而向0位移处移动时,阻尼力并未随位移变化而增大,而是保持在0左右,空程大小在0～10 mm之间,与棘轮齿距有关。分析认为,棘轮顺时针旋转时,阻尼器处于受压状态,阻尼力几乎为0;但当棘轮改变为逆时针旋转时,棘轮的外齿不一定正好卡住内齿,因此无法立刻带动内齿运动,需要外齿经过一小段的空转才能与内齿啮合,然后带动内齿运动,即会产生相应的“空程”现象,这在一定程度上影响了阻尼器的耗能能力,不利于阻尼器发挥最优性能。

部分工况中,当阻尼器结束空程部分时,阻尼力迅速增加到较大的数值,然后又下降到比较稳定的值。例如在工况11中(图4b),阻尼力增加到20 kN,然后又下降了约1.5 kN,之后在受拉阶段均稳定维持在18.5 kN。上述现象与棘轮反向转动时,摩擦副由动摩擦转变静摩擦再转变动摩擦的过程相关。文献[14]表明,不同摩擦材料接触面间静摩擦力与滑动摩擦力差别大,选用滑动摩擦力衰减小、性能良好的材料有利于保证摩擦耗能系统稳定性以及抗震性能的发挥。