岩石地球化学数据挖掘及弱异常识别——以新疆阿舍勒铜矿为例

郑超杰, 刘攀峰, 2, 罗先熔*, 文美兰, 黄文斌, 刘 刚, 吴晓贵, 邱 炜, 陈泽粟, 肖 辉, 魏超城

岩石地球化学数据挖掘及弱异常识别——以新疆阿舍勒铜矿为例

郑超杰1, 刘攀峰1, 2, 罗先熔1*, 文美兰1, 黄文斌3, 刘 刚4, 吴晓贵5, 邱 炜6, 陈泽粟7, 肖 辉7, 魏超城7

(1. 桂林理工大学 地球科学学院, 广西 桂林 541006; 2. 桂林理工大学 环境科学与工程学院, 广西 桂林 541006; 3. 中国建筑材料工业地质勘查中心 广西总队, 广西 桂林 541002; 4. 宁夏回族自治区地质矿产 勘查院, 宁夏 银川 750021; 5. 新疆维吾尔自治区地质矿产勘查开发局, 新疆 乌鲁木齐 830000; 6. 青海省地质调查院, 青海 西宁 810012; 7. 新疆哈巴河阿舍勒铜业股份有限公司, 新疆 阿勒泰 836700)

勘查地球化学找矿工作的重点在于正确解译地球化学数据, 以便从冗杂的地质信息中精准提取与成矿有关的异常信息, 指导找矿研究。然而, 地球化学数据属于成分数据, 具有闭合效应, 只有对数据进行正确的预处理才能应用多元统计分析方法, 还原元素真实的空间分布。本文在阿舍勒铜锌矿区外围南侧区域共收集1009件地表原生晕样品, 对样品中的13种微量元素进行测试, 并对原始数据、对数及ilr变换后的数据进行EDA分析, 对比数据空间分布及内部结构特征。运用(稳健)主成分分析, 结合成分数据双标图及第一主成分点位图, 解译三类数据指示的元素组合与成矿信息之间的关联。随后运用多重分形滤波技术, 对以ilr变换为基础的稳健主成分得分数据分解元素组合异常和背景分布特征。结果表明: ①经过对数及ilr变换后的数据相比原始数据空间尺度更均匀, 数据近似正态分布; ②三类数据双标图表明, 仅ilr变换后的数据消除了“闭合效应”, 且其第一主成分元素分组揭示了研究区铜矿化与铅锌多金属矿化组合; 以对数变换与ilr变换为基础的第一主成分点位图表明, 后者主成分得分异常能够较好指示研究区地质找矿信息; ③结合研究区地质找矿信息、元素组合异常及背景空间分布特征, 最终圈定3个有利找矿靶区。

成分数据分析; 多重分形; 深边部找矿预测; 新疆阿舍勒

0 引 言

在复杂的地质成矿作用过程中, 元素地球化学分布模式受多成因、多期次地质活动影响, 元素异常场与若干地质背景场反复叠加, 进而矿致异常呈现弱缓复合的叠加信息, 在空间尺度常表现为多元素共生组合关系(成秋明, 2001a; 韦导忠等, 2018)。准确了解元素的地球化学分布模式, 有效识别和分离元素地球化学数据“异常”及“背景”分布成为找矿工作的重点研究课题; 如何解译和分解这项复杂的工程, 要求地质学家不仅要对研究区的地质背景了如指掌, 也需要他们具备精湛的数据处理分析能力。成秋明等人指出: 运用分形、多重分形分析方法处理地球化学数据, 能够快速有效地从冗杂的地质信息中分离出地球化学背景和异常, 提取找矿或污染(异常)信息, 了解元素的地球化学分布模式(成秋明, 2001b; 成秋明等, 2009a)。

自Mandelbrot (1983)在《自然分形几何》中引入分形概念后, 分形理论逐渐步入大家的视线, 并被广泛应用于自然科学的众多领域中。在这之前, 地球化学家对元素在自然界的分布仅停留在其满足正态或对数正态分布(Ahrens, 1954)。随后, 国内外学者对元素地球化学场分布机制进行研究后认为, 元素含量具有尺度不变性, 地质过程包括矿化过程均可形成具有自相似性或统计自相似性的场——多重分形场(Bölviken et al., 1992; Claude et al., 1995; Cheng, 1999; 龚庆杰等, 2001); 成秋明在对非线性和复杂性理论研究的基础上, 率先提出基于分形多重分形理论的“奇异性‒广义自相似性‒分形谱系”非线性矿产资源定量预测模型, 用于开展矿产资源综合预测和定量评价工作(成秋明, 2003)。此外, 基于分形多重分形理论构建的异常、背景分离模型也不断被学者提出, Cheng et al. (1994, 2000)提出含量面积多重分形模型(concentration-area,-)和能谱面积多重分形模型(spectrum-area,-), 对地球化学数据进行异常识别和提取; 李长江等(1999)对径向密度律函数进行研究后, 将函数中的密度参数替换为距离, 使其遵循分形幂律函数, 进而提出含量距离多重分形模型(concentration-distance,-), 用于分离复杂地质背景中与成矿作用相关的异常; Afzal et al. (2011) 提出含量体积多重分形模型(concentration-volume,-), 用于识别元素异常背景分布。上述多重分形模型均为基于频率与空间分布的地球化学数据处理方法, 不同于基于频率分布的常规方法, 前者在处理地球化学数据时, 同时考虑了数据的地理位置和统计学特征(Zuo et al., 2013)。长期以来, 该理论及方法技术在国际上被广泛运用于勘查找矿(Cheng et al., 1996; 成秋明等, 2009b; Zuo, 2011, 2016b; 成秋明, 2012)及环境地球化学(Lima et al., 2003, 2005, 2008; Albanese et al., 2007)工作中。

地球化学数据属于成分数据, 具有闭合效应, 空间类型为Aitchison几何空间, 其样本空间为单形空间(simplex)。成分数据的特点表现为各组成部分的总和为一定值(定和问题), 且各部分数据相对整体具有相对性(Lloyd et al., 2012; Filzmoser et al., 2018)。由于这种效应, 因此在处理地球化学数据时, 样品中某一元素含量增减会伴随着其他各元素含量的改变, 这种改变可能导致元素间的相关性发生逆向转变(正相关‒负相关)。通常情况下, 为了快速有效的了解地球化学数据的结构及分布情况, 统计学方法是必要手段。然而, 运用统计学方法进行数据处理的前提是数据属于欧式空间, 处理成分数据若不对数据进行相应变换, 则无法得出理想的结果, 甚至会是错误结果。Aitchison (1982)在对成分数据进行研究后, 提出对数比变换方法, 旨在将Aitchison空间的数据以对数比坐标系表示进而将其转换至Euclidean空间, 该变换克服了成分数据的闭合效应, 使数据可以应用多元统计学方法进行分析。大量研究实例表明, 运用基于成分数据的多元统计方法对地球化学数据进行分析, 能够更有效揭示元素真实空间分布模式, 进而准确识别、分解元素背景及异常信息(Li et al., 2003; Carlos et al., 2010; Drew et al., 2010; Wang et al., 2017; Liu et al., 2019a, 2019b, 2020; Lin et al., 2019)。

阿尔泰造山带是世界上著名的火山成因块状硫化物(VMS)铜多金属成矿带之一(杨富全等, 2016), 阿舍勒铜锌矿床则位于该造山带西南缘阿舍勒盆地之中。前人对该矿床含矿火山岩形成的构造环境、岩相学、地球化学、矿床特征、矿物学、成矿流体、成矿物质来源、年代学、成矿机制和成矿预测进行了详细的研究工作, 并取得了一系列重要成果(陈毓川等, 1996; 吴玉峰等, 2015), 但鲜有对矿床原生晕做过系统研究。由于阿舍勒铜矿埋藏深、开采难度大、维护成本高, 并伴随着矿山开采对已探明的资源储量不断消耗, 矿体品位下降, 对阿舍勒铜锌矿床深部及外围找矿任务已迫在眉睫。在常规找矿工作效果不理想的情况下, 笔者在新疆地矿局四队的帮助下, 首次在阿舍勒矿区, 以成分数据分析视角, 对矿区外围南侧地表原生晕数据进行多元统计分析, 运用-能谱面积多重分形模型, 对地球化学元素的空间分布模式进行分离,圈定有利成矿前景区, 为矿区深部及外围找矿提供了依据。

1 研究区地质背景

1.1 区域地质背景

阿舍勒铜锌矿区位于阿尔泰地槽褶皱系琼库尔阿巴宫褶皱带西段之阔勒德能复向斜南西冀, 阿尔泰造山带南缘阿舍勒火山‒沉积盆地内。大地构造位置属于中亚造山带阿尔泰南缘晚古生代弧间拉张盆地。区域出露上志留统‒下泥盆统康布铁堡组、下泥盆统托克萨雷组、中泥盆统阿勒泰组、中泥盆统阿舍勒组、上泥盆统齐也组及下石炭统红山嘴组(杨富全等, 2013; 郑义等, 2015)。区内地质构造复杂, 主要发育NW向阔勒德能复向斜及加曼哈巴复背斜等大型褶皱, NW-SE向玛尔卡库里断裂及别斯萨拉大断裂(图1; 杨富全等, 2016)。阿舍勒盆地岩浆岩活动强烈, 发育火山岩、侵入岩和脉岩等。区域矿产资源丰富, 以有色金属、贵金属、稀有金属和白云母著名。矿产分布与区域地层构造关系密切, 以玛尔卡库里大断裂为界, 北东侧归克兰成矿带, 南西侧属额尔齐斯成矿带。沿琼库尔‒阿巴宫褶皱带中发育阿舍勒铜锌矿、喀音布拉铜锌矿、铁木尔特铅锌矿、恰夏铜矿、蒙库铁矿和可可塔勒铅锌矿等矿床, 构成克兰海西期Cu-Pb-Zn-Au- Ag-Fe成矿带(Zheng et al., 2020, 2021)。

1.2 矿区地质特征

矿区内主要出露中泥盆统阿舍勒组(D2), 上泥盆统齐也组(D3)和第四系沉积物(Q), 局部出露少量中下泥盆统托克萨雷组(D1-2)(图2)。其中, 中泥盆统阿舍勒组为赋矿地层, 主要分布于矿区中部、南部及东北侧区域。根据岩性差异可将阿舍勒组分为2个岩性段: 第一岩性段以凝灰岩为主, 局部夹结晶灰岩。第二岩性段与第一段岩性呈整合接触, 为中酸性火山碎屑岩夹少量基性熔岩。依据岩石组合又可将第二岩性段分为三个亚段, 分别为下亚段(D22a)的中酸性火山碎屑岩, 以变凝灰岩、角砾凝灰岩为主, 为本区第一个含矿层; 中亚段(D22b)的中酸性火山碎屑岩和火山‒沉积碎屑岩类, 为本矿区第二个含矿层, 其中, 矿区一号铜锌矿体及Ⅰ号蚀变带则赋存于此; 上亚段(D22c)为玄武岩夹少量沉凝灰岩及金属硫化物薄矿层。

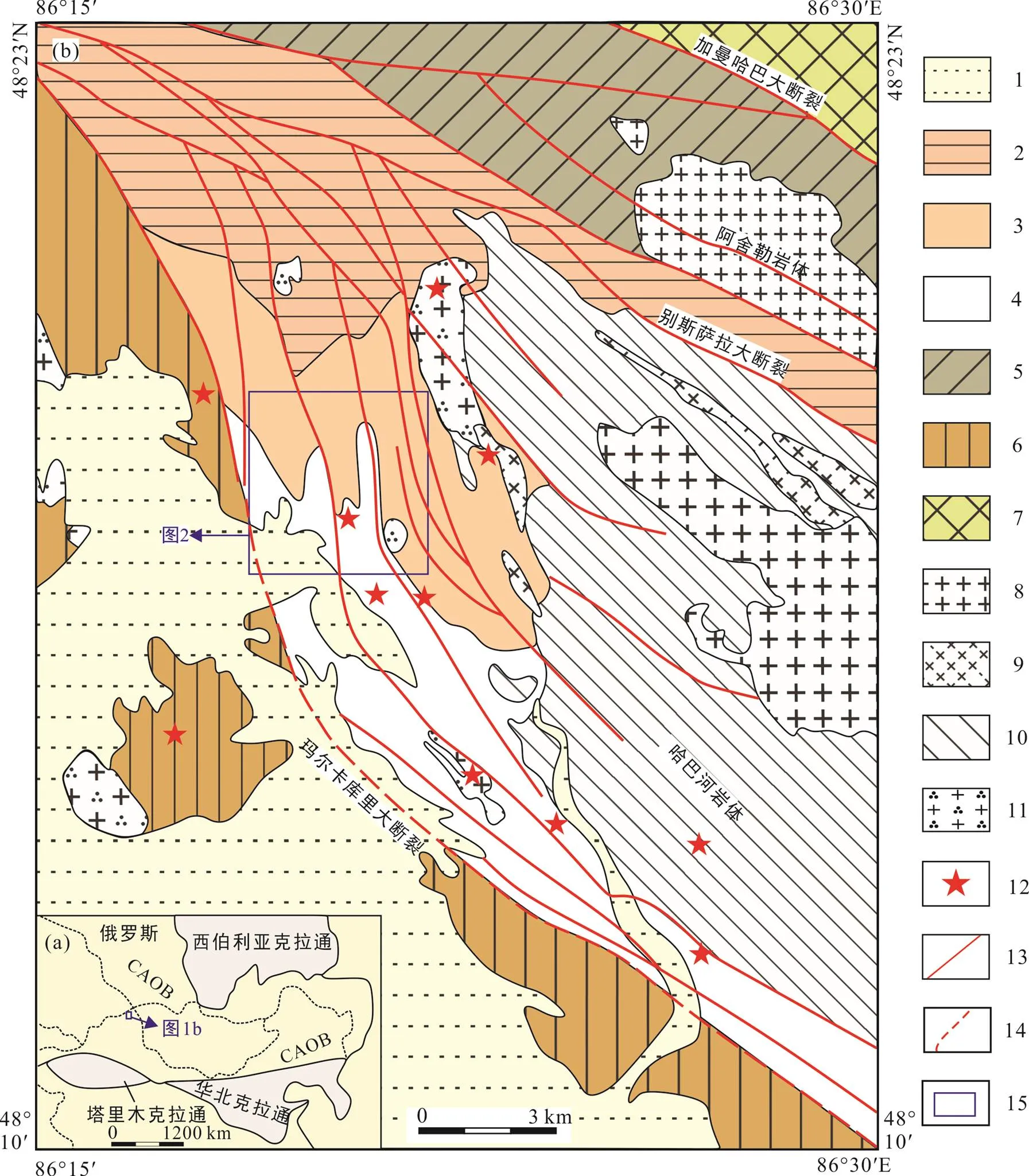
1. 中新生界沉积物; 2. 红山嘴组凝灰岩、英安岩、安山岩; 3. 齐也组火山角砾岩、凝灰岩、安山岩; 4. 阿舍勒组玄武岩、流纹岩和凝灰岩; 5. 阿勒泰镇组片岩、变质砂岩、变质粉砂岩; 6. 托克萨勒组砂岩、粉砂岩; 7. 康布铁堡组变粒岩、片麻岩和变流纹岩; 8. 花岗岩; 9. 辉长岩和辉长闪长岩; 10. 英云闪长岩; 11. 石英闪长岩和闪长岩; 12. 矿点; 13. 断层; 14. 推测断层; 15. 研究区。CAOB. 中亚造山带。

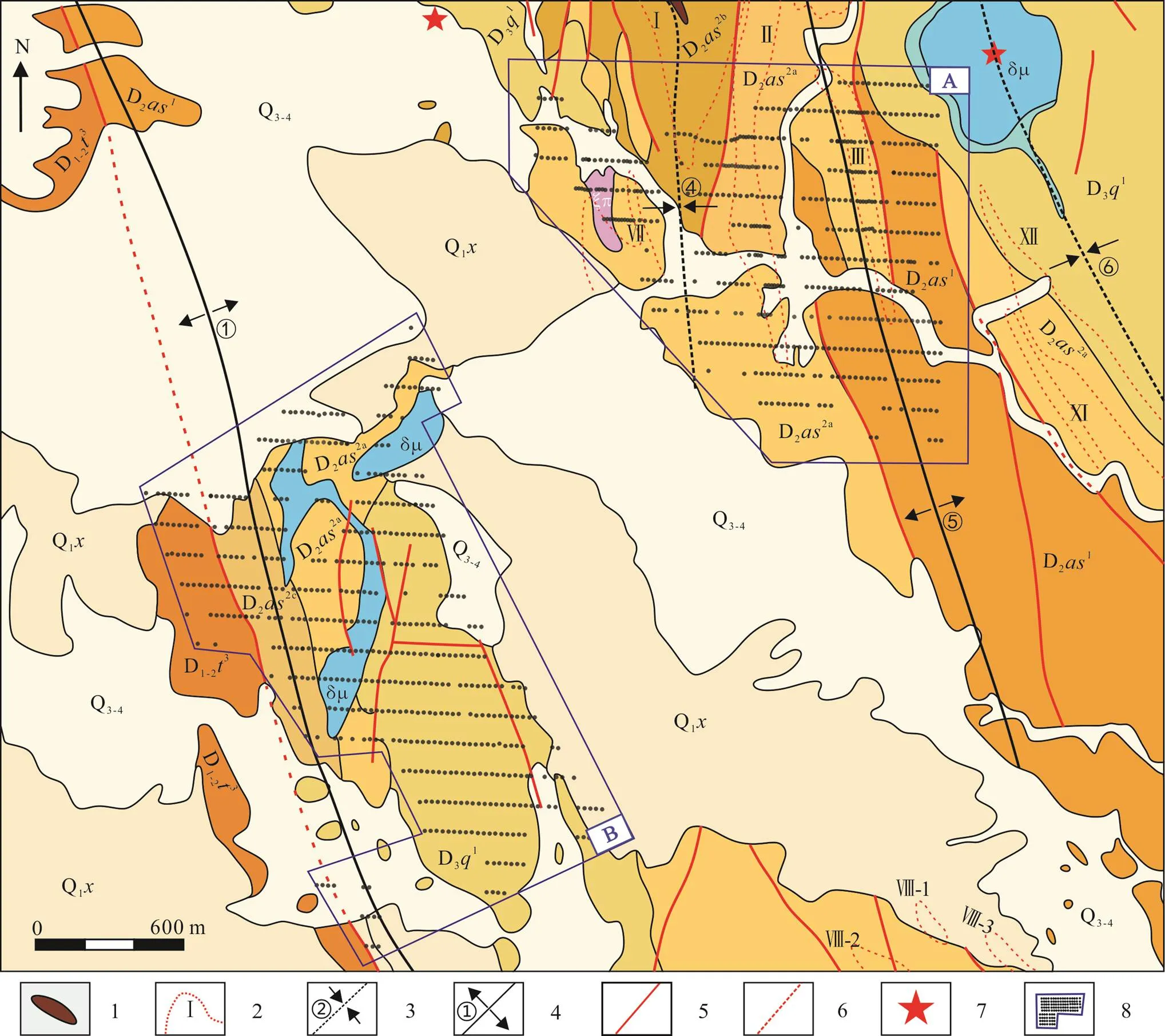
1. 铁帽; 2. 蚀变带; 3. 向斜; 4. 背斜; 5. 断层; 6. 隐伏断层; 7. 古火山机构; 8. 研究区岩石地球化学采样点位。Q1x. 第四系上更新统‒全新统沉积物; Q3-4. 第四系下更新统西域组; D3q1. 齐也组一段; D2as2c. 阿舍勒组二段上亚段; D2as2b. 阿舍勒组二段中亚段; D2as2a. 阿舍勒组二段下亚段; D2as1. 阿舍勒组一段; D1-2t3. 托克萨雷组三段; ξπ. 英安斑岩; δμ. 次闪长岩; βμ. 次辉绿岩。

矿区地质构造复杂, 褶皱、断裂十分发育。受玛尔卡库里断裂及别斯萨拉大断裂影响, 区内发育大量S-N向和NW向次级断裂, 构造表现为多期活动特点; 受动力变质及热液变质作用影响, 沿断裂普遍发育破碎带, 带中有不同程度的碎裂岩化、高岭土化、绢云母化和绿泥石化等蚀变现象。矿区范围内共圈定矿化蚀变带15条, 呈NW向和近S-N向展布, 与研究区地层及主要次级断裂走向基本一致。其中, 主要有五种蚀变组合: ①黄铁矿化‒绢云母化‒强硅化组合; ②黄铁矿化‒绢云母化‒硅化组合; ③绢云母化‒绿泥石化‒黄铁矿化‒弱硅化组合; ④似矽卡岩化‒黄铁矿化组合; ⑤绢云母化‒高岭土化组合。

目前, 矿区已发现的一号铜锌矿体产于中泥盆统阿舍勒组二岩性段的Ⅰ号矿化蚀变带中, 空间上位于④号向斜及多条断裂交汇处。该矿床形成与中酸性火山(沉积)岩有关, 主要属于火山喷气‒沉积成因, 并在后期遭受了变形变质热液叠加改造形成的块状硫化物铜锌矿床, 显示典型的海底火山喷气‒沉积矿床的共同特点, 矿石构造具有典型的双层结构(杨富全等, 2016)。

2 样品采集与数据处理

2.1 样品采集及测试分析

对矿区南侧约3.8 km2的A、B两个区域, 按照20 m×100 m测网共采集地表原生晕样品1009件, 样品采集流程严格遵守1∶10000岩石地球化学测量规范(DZ/T 0248-2014)。所采集样品均为新鲜基岩, 每份样品为该采样点周围5 m内同种类型岩石近等质量的组合样, 每份样品重量不低于300 g; 随后将野外采集样品于室内破碎, 低温烘干, 磨机研磨至过200目网筛, 存样待测分析。

本次样品测试分析工作由新疆第四地质大队实验室承担, 定量分析测定Cu、Zn、Pb、Ag、Au、As、Sb、Bi、Mo、Sn、Ba、Co、Cd等13个元素; 样品测试按照行业标准DZ/TO130.4-2006执行, 分析质量达到标准要求; 13个元素的分析方法及检出限见表1。

2.2 基于成分数据的多元统计分析

地球化学元素分布规律的研究是揭示元素矿化富集及空间变化规律的重要途径之一(成秋明, 2000)。地球化学数据在受到“异常”干扰时往往呈偏态分布, 这些“异常”一部分是由于地壳元素空间分布不均匀造成的, 其次则是受到各种内、外动力地质作用对元素再分配的影响, 更有甚至是受人为活动干扰。大部分统计学方法在对数据进行处理时, 要求数据尽可能服从正态或对数正态分布, 各变量之间的关系为线性关系(胡以铿, 1991; 陈健, 2019)。探索性数据分析(EDA)属于稳健统计学范畴, 该方法的优势在于无需要求数据服从正态分布, 通过箱型图、散点图、直方图、累计密度分布函数等简单图示, 能快速、准确得出数据的内部结构及聚散分布特征(何旺等, 2020)。此外, Hampel (1974)年提出中位数绝对离差(MAD)这一估计量, 该估计量不受样本量及少量离群值的影响, 常被用来检验数据中的离群值(Reimann et al., 2011; Leys et al., 2013)。

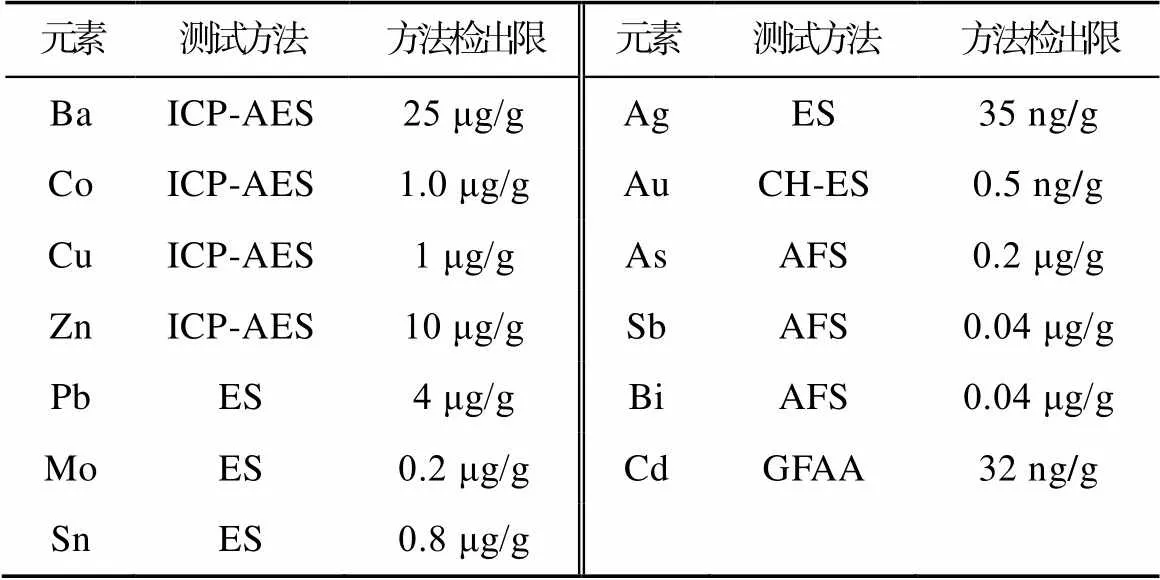
表1 测试方法及质量参数表

注: ICP-AES. 等离子体光谱仪; ES. 光谱深孔电极; CH-ES. 化学光谱; AFS. 原子荧光光谱; GFAA. 石墨炉原子吸收。

目前, 针对成分数据进行对数比变换的方法分为3种, 分别是由Aitchison (1982)年提出的alr(additivelogratio coordinates)和clr(centered logratio coefficients)变换, 及由Egozcue et al. (2003)提出的ilr(isometric logratio and pivot coordinates)变换。其中, clr和ilr变换为等距变换, alr变换为非等距变换, 等距变换后的数据在变换前后保持样本空间距离不变(Lloyd et al., 2012; Filzmoser et al., 2018)。Pawlowsky-Glahn and Egozcue (2006)在对等距变换方法研究后指出, 相对clr变换, ilr变换克服了由clr变换后造成的协方差矩阵奇异性问题, 更适用于实际数据处理, 但缺点是数据进行ilr变换后会减少变量个数, 致使变换后新变量无法直接解译原始变量(Pawlowsky-Glahn and Egozcue, 2006)。随后, Filzmoser (2009)研究发现, 通过对成分数据进行ilr变换再运用稳健主成分分析(RPCA), 随后将所得主成分得分和载荷值通过标准正交基逆转换至clr坐标系, 该方法不仅解决了ilr变换后新变量难解译的问题, 同时解决了clr变换后协方差矩阵的奇异性问题(Pawlowsky-Glahn and Egozcue, 2006; Zuo et al., 2013)。此外, RPCA通过对数据中的离群值进行预处理, 避免了主成分分析(PCA)因数据离群值存在而产生有偏的协方差矩阵估计量。Gabriel (1971)提出双标图的概念, 将数据矩阵的成分得分和载荷值以双标图展示, 能够可视化数据集中样本和变量关联(Gabriel, 1971; 马艳芳, 2016); 随后, Aitchison and Greenacre (2002)详细阐述了成分数据双标图的应用。

本次研究涉及的ilr及clr对数比变换公式如下所示:

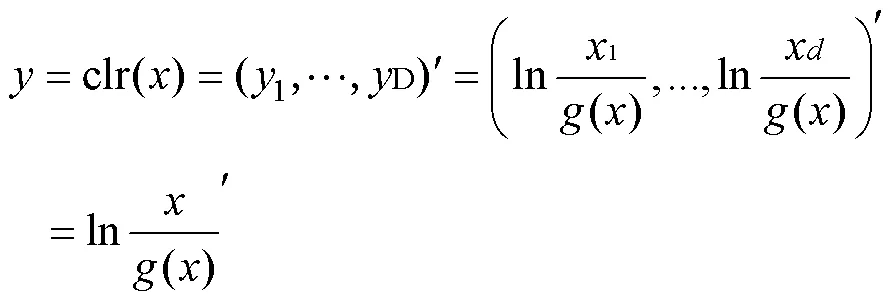
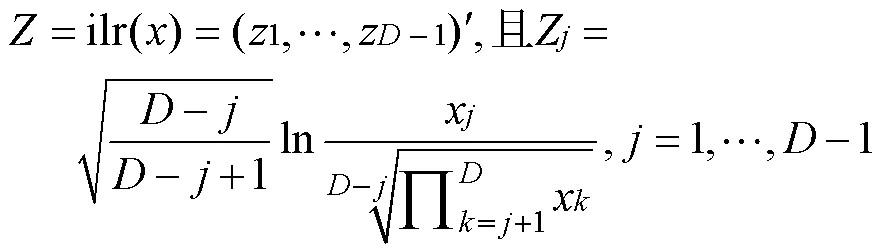
其中,()是以为变量的几何平均值, 其公式为:

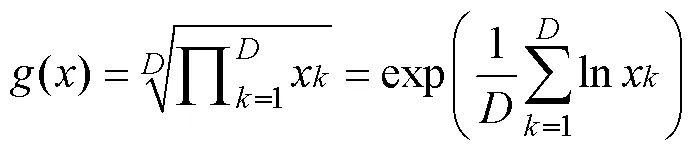
(1) 式中变换将属于维单形空间的变量以一对一方式映射至维向量空间变量中; (2)式中ilr变换以Z为枢纽中心, 将属于维单形空间的变量映射到−1维的超平面向量空间中。

为了探究地球化学数据变换前后数据的内部结构及分布情况, 以及ilr变换处理数据的可行性。本次研究对原生晕样品中13种元素的原始数据, 对数变换及ilr变换数据进行统计分析, 得出各类数据的统计学特征(表 2); 运用R统计学软件对上述数据进行EDA技术分析, 分别得出三类数据的累计密度分布曲线(图 3)及箱图(图 4); 为查明元素组合与成矿作用间的关联, 并对三类数据进行PCA/RPCA分析, 选取PC1和PC2主成分构建主成分双标图(图 5), 并在GIS地理信息系统中创建PC1主成分得分点位图(图 6)。

2.3 多重分形技术

反距离权重插值法(IDW)常被用于地球化学点位数据的栅格处理, 该方法精确且应用方便, 但忽略了数据内部结构的变异性。而成秋明提出的多重反距离权重插值法(MIDW)结合了多维分形理论和滑动加权估值方法, 克服数据本身差异性缺陷的同时, 增强了数据的局部结构信息(成秋明, 2001b; Cheng, 2008)。-模型运用傅里叶变换, 将元素地球化学场由空间域转换至频率域, 依次得出相(phase)分布图及能谱(power-spectrum)分布图; 根据元素在背景场、异常场及干扰场呈现的各向异性, 三者在傅里叶空间具备各自不同的广义自相似性, 即表征为不同特征的能谱波段; 按照能谱波段差异则能分解出三类滤波器; 随后, 运用傅里叶逆变换, 将三类滤波器分别转换回空间域, 进而提取元素背景, 异常空间分布。其中, 三者在频率域中自相似性差异可由幂律(分形或多重分形)模型体现, 即满足(≥) ∞−β, 表达式中表示能谱密度,(≥)是在能谱密度空间中超出的面积,为分形模型的指数(成秋明, 2006b); 根据幂律模型将能谱密度与累计面积在双对数坐标中表示, 并运用最小二乘法拟合, 得出线性关系, 进而分解各类滤波器。其中, MIDW插值法及-模型等系列理论由成秋明等人提出(成秋明, 2001b, 2006a, 2007), 并在相关学者的研究下不断拓展、推广(Zuo et al., 2012; Zuo and Wang, 2016a)。

为查明研究区元素组合的异常及背景空间分布, 本次研究运用GIS软件对ilr变换为基础的PC1、PC2稳健主成分得分数据, 应用MIDW插值法栅格数据, 借助-模型分解元素异常及背景特征; 其中, 数据栅格及-模型, 借助中国地质大学GPMR国家重点实验室成秋明团队开发的Geodas矿产资源定量预测系统, 及左仁广团队开发的基于Arcgis地理信息系统的Arcfractal插件完成(Cheng et al., 2001; Zuo and Wang, 2020)。

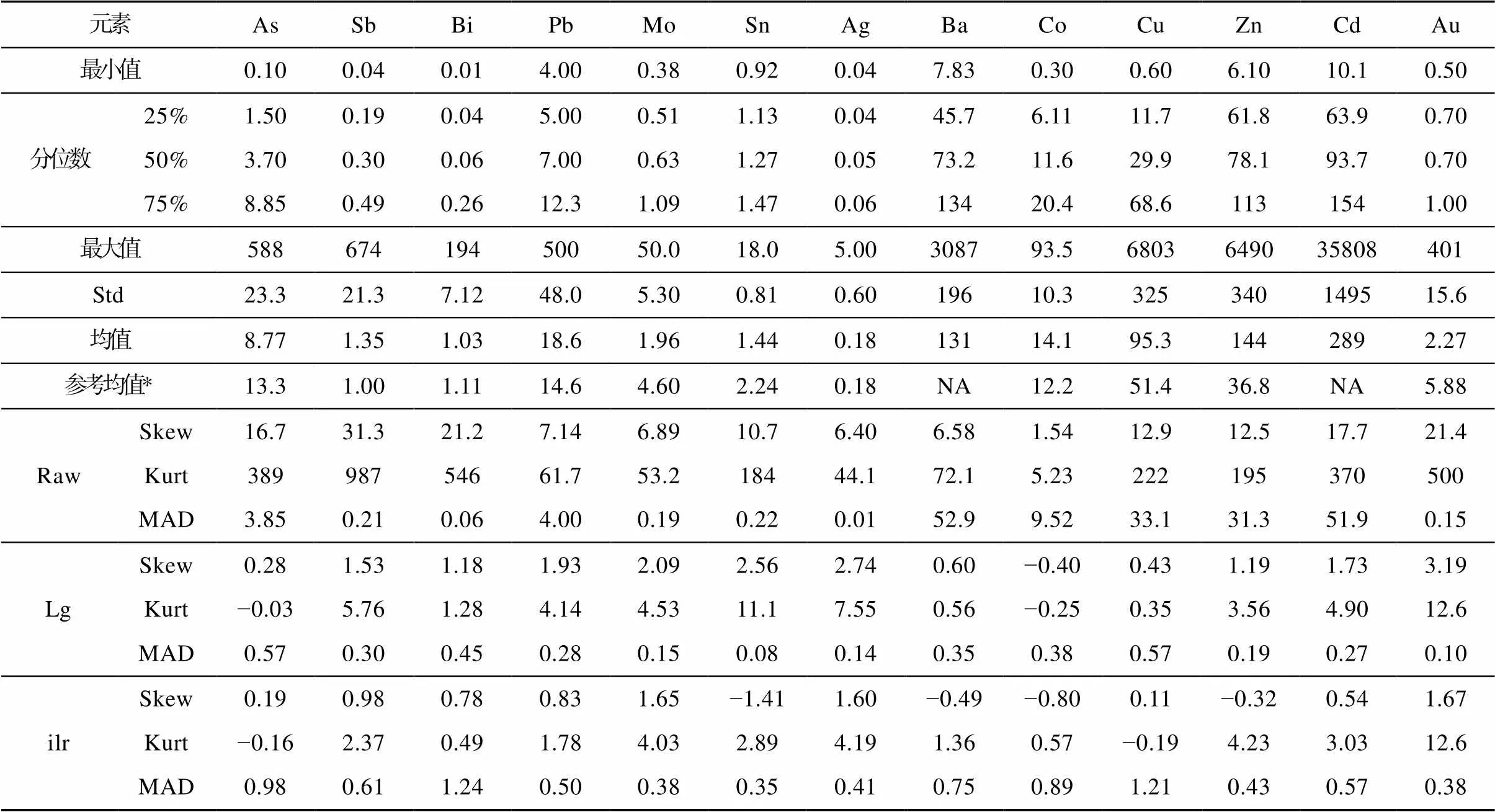
表2 原始数据、对数变换及ilr变换数据统计信息

注: 元素含量单位, 除Au为ng/g, 其余元素均为μg/g; 参考均值*引用自阿舍勒矿区地表岩石实测算数平均值(陈毓川等, 1996); NA: 表示数据缺失; Std: 标准差; Skew: 数据偏度; Kurt: 数据峰度; MAD: 中位数绝对偏差。

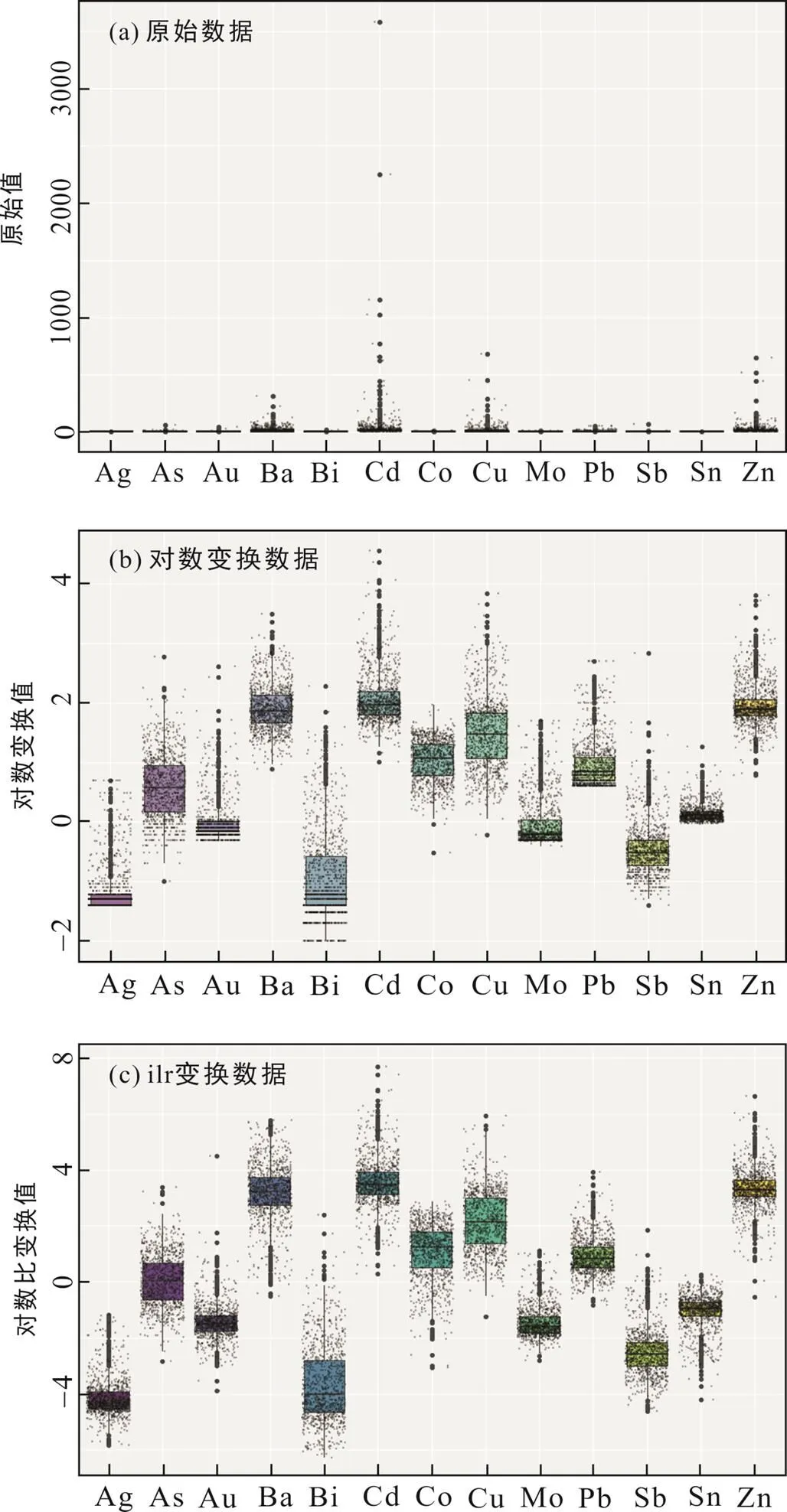
图3 原始数据(a)、对数变换数据(b)和ilr变换数据(c)箱图

3 结 果

3.1 EDA技术

从表2可以看出, 原始数据各元素含量在数量级上差异极大, 多数元素(Sb、Bi、Cd、Au)的最大值与均值之比超过100, 主成矿元素(Cu、Zn、Pb、Au、Ag)的比值也介于27～177之间; 将本次研究区各元素均值与一号矿体地表岩石含量均值(陈毓川等, 1996)相比, 可见主成矿元素Cu、Zn含量远超矿区地表岩石元素含量; 不难看出, 在仅3.8 km2的研究区内, 元素空间分布差异性大, 而研究区主成矿元素与矿区地表原生晕含量相当, 表明研究区同样具备较大成矿潜力。对比表中三类(Raw、Lg、ilr)数据, 对数变换和ilr变换能够极大程度上使数据趋于正态化, 变换后各元素偏态(Skew)和峰态(Kurt)均得到显著改善, 符合正态分布特征。此外, 表2中原始数据的MAD值与原生晕各元素含量均值相差很大, 表明研究区受各类地质作用影响, 元素在空间分布上差异性极强。

从箱图及密度曲线可知, 原始数据空间尺度差异大, 数据分布较分散, 多数元素存在大量高值异常点; 其中, 原始数据的累计密度曲线因数据之间量级及尺度差异较大(未在此处展示)。而经过对数及ilr变换的数据, 各元素空间分布尺度差异性大幅降低, 均处于同一数量级, 数据箱图空间展布更加均匀, 对应密度曲线也近似呈单峰/多峰正态分布。进一步对比对数及ilr变换后的箱图特征可知, ilr变换(图3c)后的数据无论在空间尺度或是数据内散度上都比对数变换(图3b)后的数据更集中、均衡, 且前者具有更佳的近似对称的高低极值分布, 相应的密度曲线也较后者更接近正态分布(图4a、b)。不难看出, 经过变换处理的数据能够极大程度降低数据内部的不均一性, 消除数据的偏态分布, 使数据趋于集中, 符合多元统计分析要求; 而相比对数变换, ilr对数比变换则能进一步消除数据内部的不均衡性, 使数据呈正态分布。

3.2 主成分双标图

图5依次展示了原始数据、对数变换数据及ilr变换数据经过PCA及RPCA分析所得的PC1、PC2主成分双标图。其中, 以ilr变换为基础的数据(图5c、d)在经过PCA及RPCA分析后, 变量(元素)数据被打开, 整体呈放射状, 闭合效应已消除; 而原始数据及对数变换后的数据(图5a、b)经PCA分析后, 变量依旧呈现一边倒的趋势, 即数据依旧存在闭合效应。其次, 经过变换为基础的主成分数据(图5b、c、d)拥有比原始数据(图5a)更高的PC1、PC2总方差解译值, 而经过RPCA分析的ilr变换数据(图5d)拥有远超其他数据的PC1主成分方差解释值, 表明消除离群值影响所得的成分更具代表性。此外, 图5中四幅图的PC1成分方差解译值均大于PC2成分方差解译值, 表明PC2主成分蕴涵的信息远不如PC1主成分具有代表性。

从主成分双标图确定的元素组合方面来看, 原始数据(图5a)和对数变换为基础的主成分双标图(图5b)呈现类似的元素组合。两者的PC1成分中仅Co元素载荷值为负, 其余元素均为正载荷, 无法得出各元素之间的关联; 虽然两者在PC2成分中表现出细微的差异, 但两者元素间分布模式十分类似, 依旧无法查明元素组合与成矿的关系。相比之下, ilr变换为基础的主成分双标图(图5c、d), 元素分布模式与前者截然不同; 后者经过ilr变换, 成分数据被打开, 因此两者在双标图中呈现类似的元素组合, 其差别在于RPCA(图5d)相比PCA方法(图5c)排除了数据内离群值的干扰, 元素组合更准确。最后, 从图5d中PC1成分可以明显分出两个元素组合, 分别是以Cu-As-Sb-Co元素代表的铜矿化组合和以Pb-Zn-Ag-Au-Mo-Ba-Cd-Bi-Sn元素代表的铅锌金银多金属元素矿化组合。

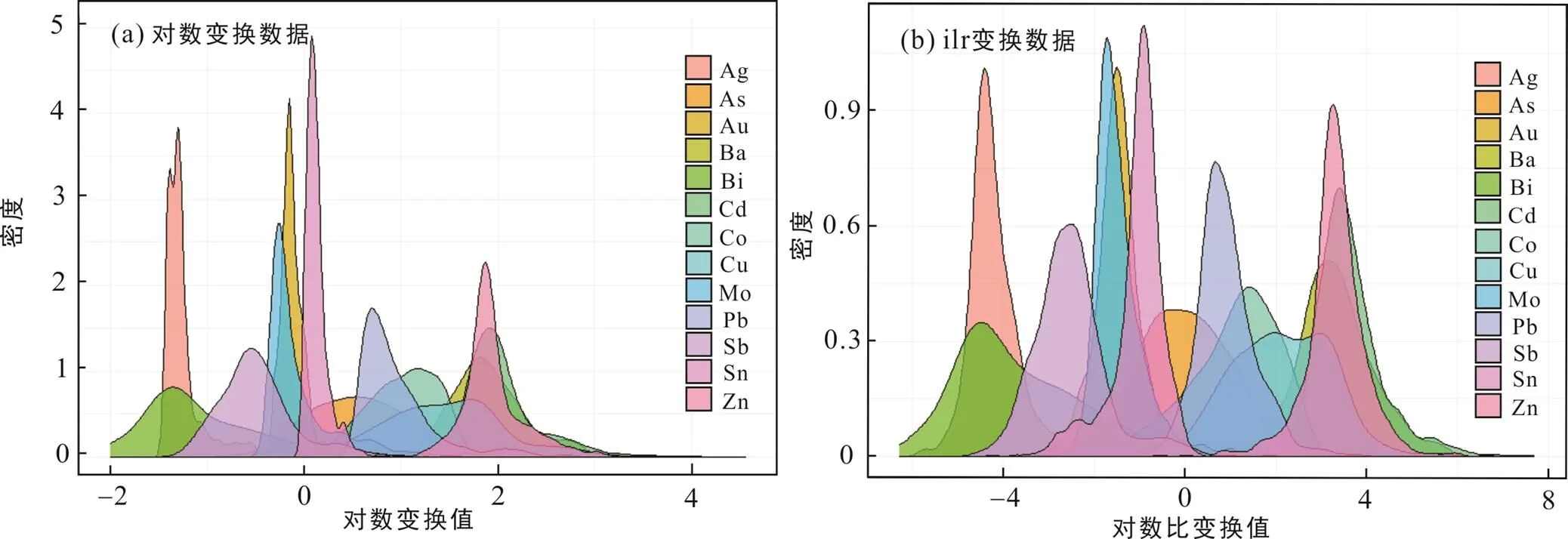
图4 对数(a)及ilr(b)变化数据后的累计密度分布曲线

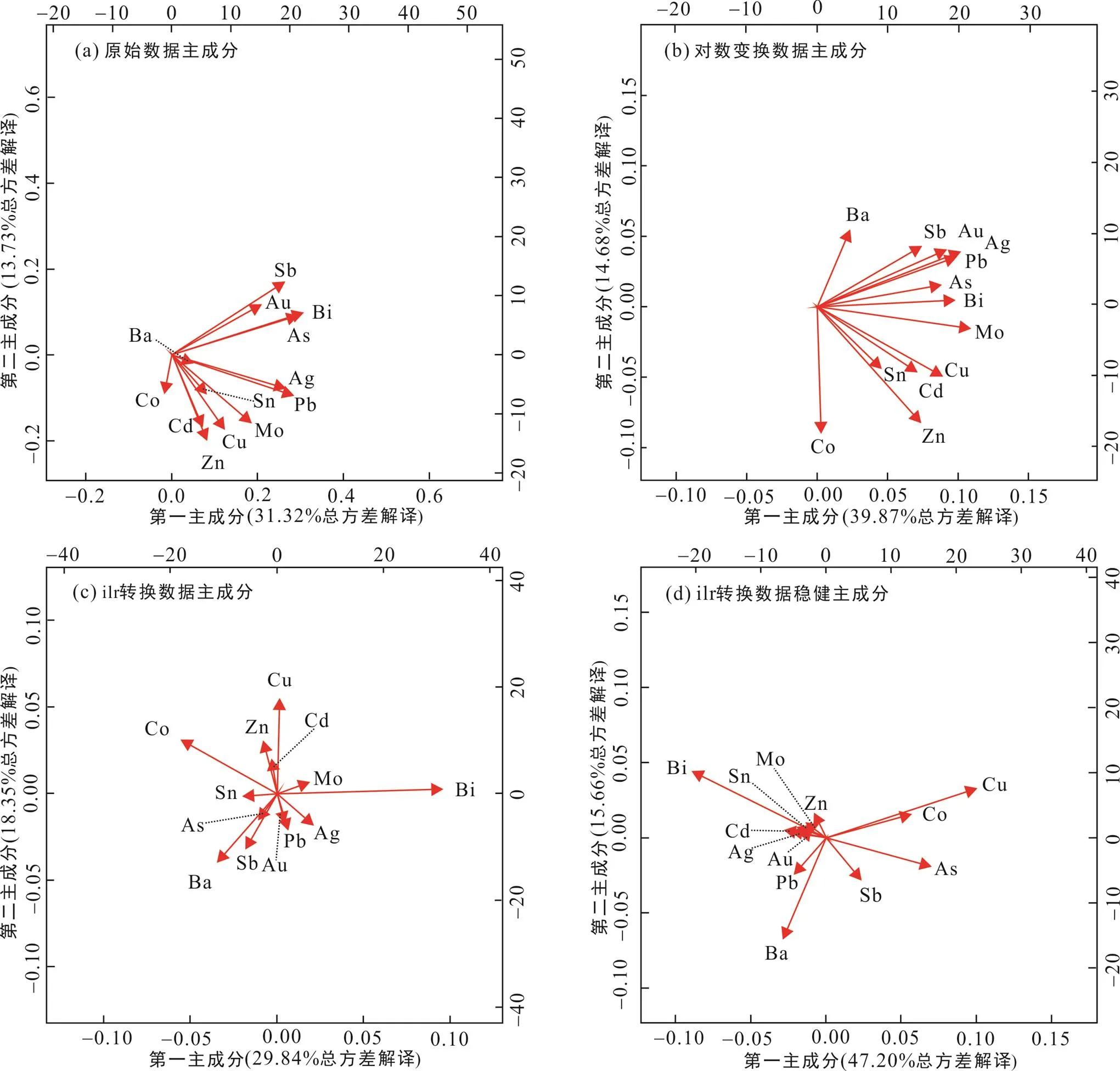
图5 研究区岩石地球化学不同类型变换数据PCA/RPCA双标图

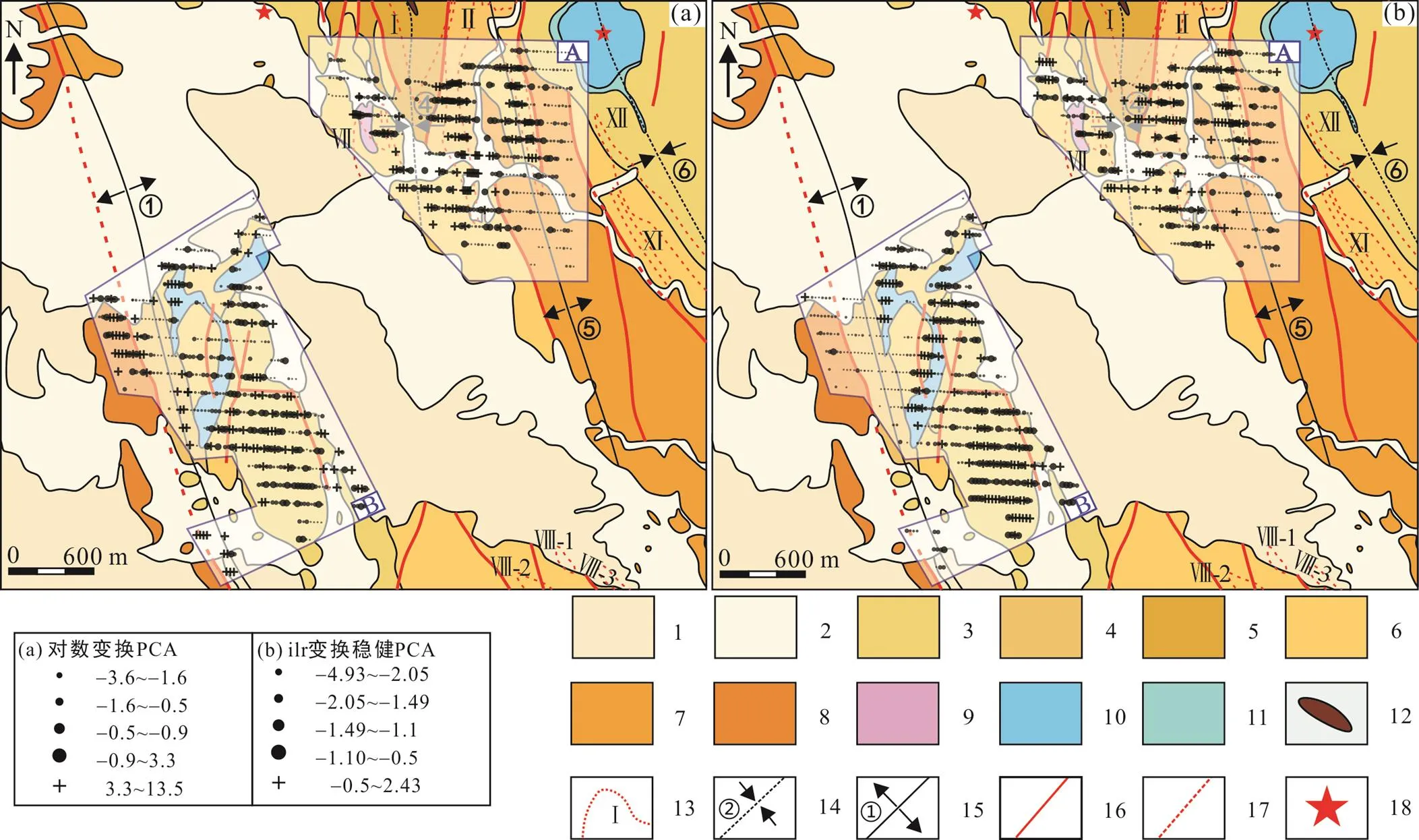
(a) PCA对数变换数据; (b) PCA对数比变换数据。1. 第四系上更新统‒全新统沉积物; 2. 第四系下更新统西域组; 3. 齐也组一段; 4. 阿舍勒组二段上亚段; 5. 阿舍勒组二段中亚段; 6. 阿舍勒组二段下亚段; 7. 阿舍勒组一段; 8. 托克萨雷组三段; 9. 英安斑岩; 10. 次闪长岩; 11. 次辉绿岩; 12. 铁帽; 13. 蚀变带; 14. 向斜; 15. 背斜; 16. 断层; 17. 隐伏断层; 18. 古火山机构。

3.3 主成分得分点位图

在各类数据双标图分析基础上, 本次研究选取具有代表性的对数变换(PCA)及ilr变换数据(RPCA, 消除离群值影响)进行主成分分析, 将所得PC1主成分得分数据(对应双标图5b、d), 绘制研究区主成分得分点位图(图6)。从点位图中可以看出, 以ilr变换为基础的RPCA数据(图6b)比对数变换为基础的PCA数据(图6a)呈现更清晰、更集中的高得分空间展布特征。其中, 图6a中A区域显示的高值空间展布, 大致与区内的Ⅱ、Ⅲ、Ⅶ号蚀变带、区内的褶皱、断裂构造的空间位置相吻合; B区域的高得分空间位置主要与该区内的几条断裂构造相吻合。结合双标图5b不难看出, 由于对数变换数据的闭合效应, 双标图无法有效界定元素组合和与成矿信息间的关系, 致使对数变换为基础的PCA数据高值分布, 反映的多是与矿化蚀变带、断裂等一系列复合叠加地质信息为主的异常特征。而图6b的PC1主成分点位图呈现的主成分高值空间分布模式则与前者有较大出入。图6b中A区的高得分区域分布于④号向斜及⑤号背斜之间区域, 空间位置与其内的蚀变带及断裂交汇处相吻合; 而B区域的高值区域一部分展布于该区的几处侵入岩体与地层交界处, 其余则分布于该区东南侧齐也组一段内。结合图5d双标图解译, PC1高值得分主要反映了研究区铜矿化组合特征。

4 靶区圈定与找矿前景分析

4.1 多重分形技术

选取ilr变换为基础的RPCA得分数据进行MIDW插值处理, 将所得栅格文件以-模型分解元素组合异常及背景, 两组数据的地球化学背景及矿化异常分解依据由图7的能谱面积-双对数图确定。由图8、9可知, 经过-模型滤波处理后, 元素组合异常特征在研究区内的空间分布更为清晰。通过对双标图(图5d)解译可知, 图8a中高异常区域对应PC1主成分中的Cu-As-Sb-Co元素组合, 即以Cu元素为主的矿化作用; 图9a中高异常则是与PC2主成分中的Cu-Zn-Au-Ag-Co-Mo-Sn-Bi-Cd元素代表以铜锌多金属为主的矿化作用。由于两类元素组合均包含Cu、Co在内的高温元素组合, 两者在异常的空间分布上存在一定相似性。其中, PC1主成分分解图(图8a)中A区域元素组合异常呈星状分布, 高值异常规模小, 空间上分别与赋矿地层、褶皱带及蚀变带位置相吻合, 尤其是三者交汇区域异常显著; B区域高值异常主要分布于侵入岩体与阿舍勒组接触带, 局部分布于齐也组三段之中; 图8b展示的PC1主成分背景分布表明, 研究区高背景多与阿舍勒组二段赋矿地层(A区)及齐也组一段(B区)吻合, 一定程度上说明-模型的准确性。在PC2主成分分解图(图9a)中, A、B两区元素组合高值异常空间形态整体较集中, 异常连续性好, 面积大, 强度高, 空间分布同样指示地表构造及蚀变带交汇处, 中、弱强度异常与区内发育的背、向斜构造及蚀变带吻合; 图9b中A、B两区的PC2成分高背景分布大致与赋矿地层相吻合。

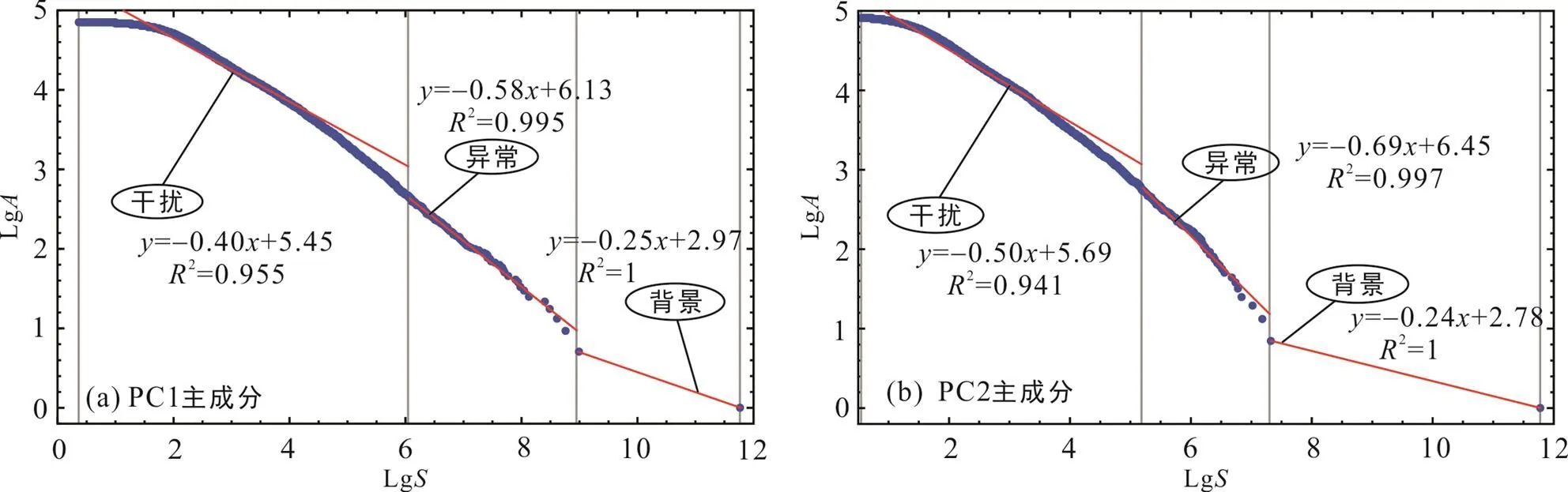
图7 对数比变换数据主成分能谱面积S-A双对数图

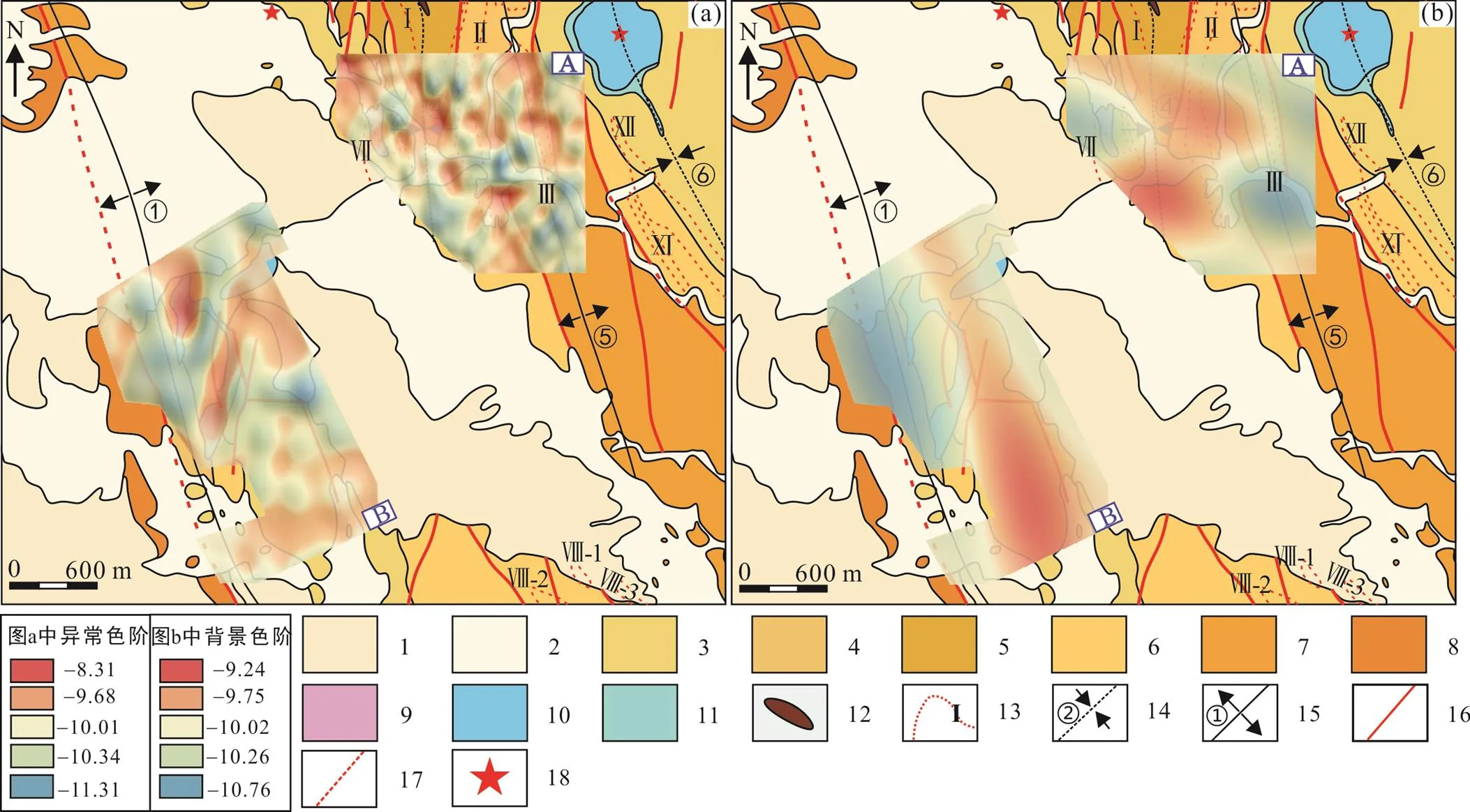
1. 第四系上更新统‒全新统沉积物; 2. 第四系下更新统西域组; 3. 齐也组一段; 4. 阿舍勒组二段上亚段; 5. 阿舍勒组二段中亚段; 6. 阿舍勒组二段下亚段; 7. 阿舍勒组一段; 8. 托克萨雷组三段; 9. 英安斑岩; 10. 次闪长岩; 11. 次辉绿岩; 12. 铁帽; 13. 蚀变带; 14. 向斜; 15. 背斜; 16. 断层; 17. 隐伏断层; 18. 古火山机构。

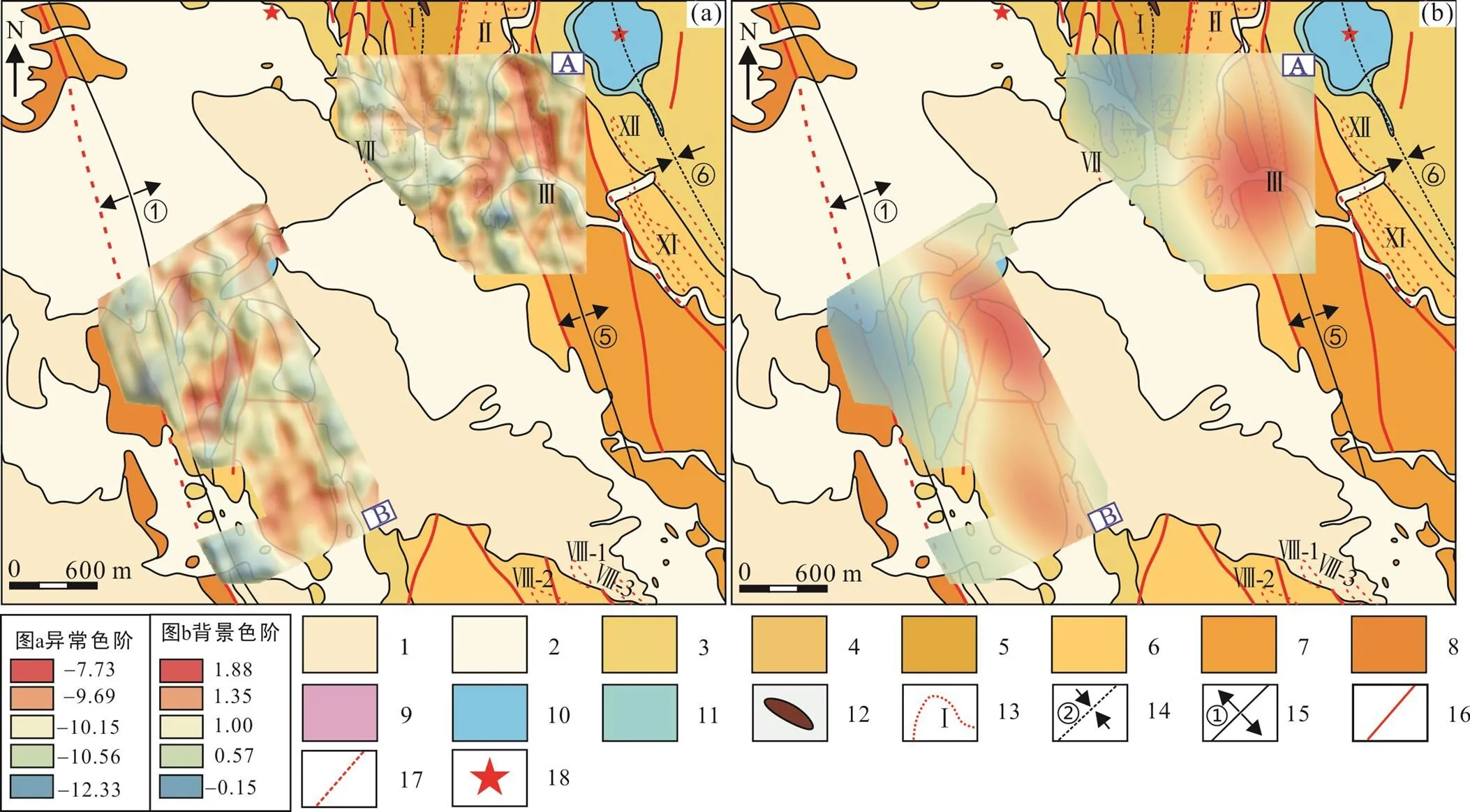
1. 第四系上更新统‒全新统沉积物; 2. 第四系下更新统西域组; 3. 齐也组一段; 4. 阿舍勒组二段上亚段; 5. 阿舍勒组二段中亚段; 6. 阿舍勒组二段下亚段; 7. 阿舍勒组一段; 8. 托克萨雷组三段; 9. 英安斑岩; 10. 次闪长岩; 11. 次辉绿岩; 12. 铁帽; 13. 蚀变带; 14. 向斜; 15.背斜; 16. 断层; 17. 隐伏断层; 18. 古火山机构。

4.2 找矿前景分析

研究区的主要赋矿地层为泥盆系阿舍勒组二段(D22), 图8、9中A区高值异常在空间上与该地层对应, 但B区东南侧齐也组一段也显示高得分异常。结合研究区地质特征(图2), 该区东、西两侧分别发育北西向的①号背斜及近S-N向的②号向斜构造。向斜构造能较大程度避免近核部地层遭受风化剥蚀, 并且已发现的一号铜锌矿体则赋存于④号向斜之中。考虑到区内出露的齐也组一段(D31)与下伏阿舍勒组二段赋矿地层呈不整合接触, 推断分布于齐也组一段的高值异常区由下伏地层引起。

区内NW向马尔卡库里和别斯萨拉两处深大断裂, 控制了研究区内次级构造的空间展布。次级断裂复合部位控制了火山机构的分布, 铜多金属矿化则环绕阿舍勒期火山口四周洼地分布(叶庆同等, 1998); 由图 8的PC1成分异常、背景分布特征可知, B区高值异常分布于研究区中部及南部, 与该区多条断裂展布及次闪长岩侵入地段吻合; B区高背景分布于南侧齐也组一段, 但北侧赋矿地层呈现低背景特征。李志纯(1996)对矿区外围岩石、远矿围岩及近矿围岩中成矿元素含量调查得出: 近矿围岩中成矿元素含量最高, 其次为矿区外围岩石, 最后为远矿围岩。上述研究表明, 受变质热动力驱动, 以PC1为代表的铜多金属成矿元素组合沿矿区构造裂隙发生了从远矿(赋矿)围岩向矿体活化转移的现象, 致使元素在侵入岩体、断裂交汇处出现异常, 而在远离矿体外围区域呈现高背景。此外, 据研究区勘探报告, 研究区共发现4处蚀变带, 其中以黄铁矿化‒绢云母化‒强硅化组合具有直接指示寻找火山喷气‒沉积型矿床的意义, 似矽卡岩化‒黄铁矿化组合为寻找火山沉积热液改造型矿床的重要标志(李志纯, 1996; 张俊杨等, 2016)。对比研究区出露的4处(Ⅰ、Ⅱ、Ⅲ、Ⅶ)蚀变带, 以Ⅰ、Ⅱ、Ⅶ号蚀变带具有直接指示寻找火山喷气‒沉积矿床的意义,Ⅲ号蚀变带具有直接指示寻找火山沉积热液改造型矿床的意义。

前人对该矿床成因系统研究后认为, 多金属成矿作用与泥盆纪火山活动密切相关, 中泥盆世中晚期火山喷发间歇期是形成块状硫化物矿床的有利成矿阶段(叶庆同等, 1998; 郑义等, 2015; 杨富全等, 2016)。由图2可知, 古火山机构分布于研究区北部, 依附于褶皱转折端, 毗邻一号铜锌矿体, 表明火山机构或为成矿物质来源的重要通道, 是推断沉积矿体空间赋存的重要线索。叶庆同等(1998)及陈毓川等(1996)对矿区成矿流体研究后发现, 阿舍勒矿床热水沉积阶段成矿温度为80～310 ℃, 在变质改造期及热液叠加期, 热液温度升至约310～540 ℃。此外, 从矿体矿物组合特征来看, Ⅰ号矿体的主要金属矿物为铜的相关硫化物, 锌作为矿床重要共生组分, 多以闪锌矿分布于铜硫矿石之间, 铅、银、金等有用组分则呈分散态赋存于Ⅱ号矿体硫化物矿石之中。结合图5d的双标图同样可得, 由PC1主成分所得的Cu-As-Sb-Co及Pb-Zn-Au-Ag-Mo-Sn-Bi-Cd两组矿化组合, 大致反映了矿床形成的两大阶段: 即与喷流沉积成矿作用相关的中低温铜多金属成矿阶段, 和与变质改造及热液叠加活动有关高温铅锌金银多金属矿化阶段。

4.3 找矿靶区圈定

通过对研究区地表原生晕地球化学数据进行系统全面的分析, 结合研究区成矿地质情况可知, 研究区有利找矿地质特征与赋矿地层、构造复合端、古火山机构、侵入岩体及蚀变带关系密切, 结合研究区元素组合异常平面分布特征, 共圈定具有找矿前景的Ⅰ类靶区两个, Ⅱ类靶区一个(图10)。各靶区特征如下:

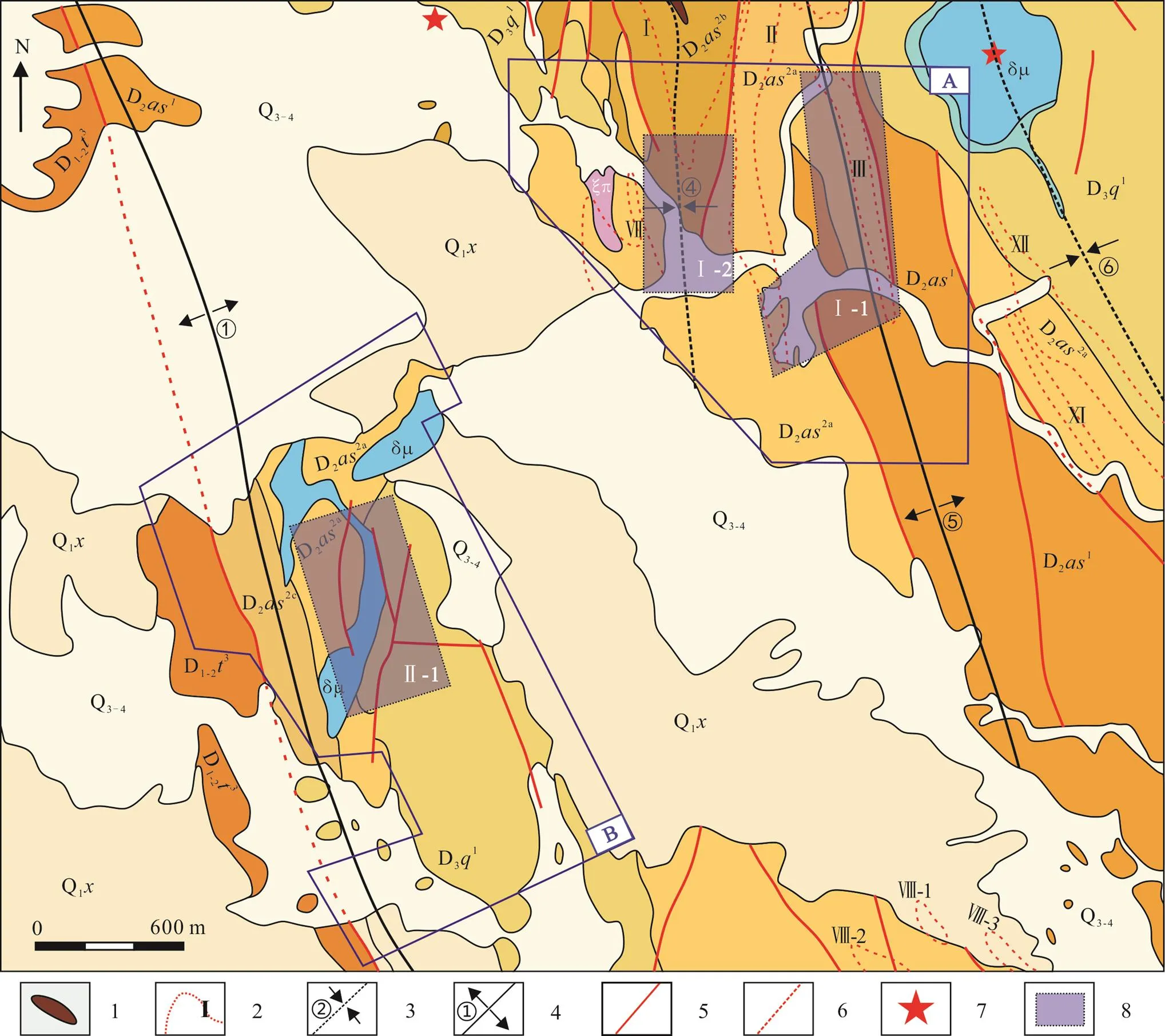
1. 铁帽; 2. 蚀变带; 3. 向斜; 4. 背斜; 5. 断层; 6. 隐伏断层; 7. 古火山机构; 8. 找矿靶区。Q1x. 第四系上更新统‒全新统沉积物; Q3-4. 第四系下更新统西域组; D3q1. 齐也组一段; D2as2c. 阿舍勒组二段上亚段; D2as2b. 阿舍勒组二段中亚段; D2as2a. 阿舍勒组二段下亚段; D2as1. 阿舍勒组一段; D1-2t3. 托克萨雷组三段; ξπ. 英安斑岩; δμ. 次闪长岩; βμ. 次辉绿岩。

Ⅰ类靶区: 该靶区主要包括位于A区内的Ⅰ-1及Ⅰ-2两个找矿有利地段。其中Ⅰ-1及Ⅰ-2区段分别位于A区东、西两侧, 空间相邻; 两有利地段存在明显的PC1及PC2元素组合高值异常, 且均位于赋矿岩层(D22)中; 与此同时, 两区段中都具备褶皱复合端、断层交汇及蚀变带等有利成矿条件, 且空间位置紧邻古火山机构。由此, 建议可在Ⅰ类成矿有利靶区内进一步开展地质勘查及深部工程验证工作。

Ⅱ类靶区: 该靶区包括一个Ⅱ-1成矿有利地段, 该地段位于B区中部; PC1及PC2主成分元素组合异常图在该区段存在显著高值异常; 与此同时, 该区段内出露阿舍勒组二段赋矿(D22)及齐也组一段(D31), 并有部分侵入岩体出露, 通过前文分析可知, 齐也组一段虽不是矿区赋矿地层, 但其下赋的阿舍勒组二段为含矿层位, 具备成矿潜质。此外, 该处还是褶皱复合端与断裂构造交汇区域, 具备赋矿条件。在此基础上, 建议可对Ⅱ类成矿有利靶区进一步开展地质勘查研究工作。

5 结 论

(1) 地球化学数据是典型的成分数据, 具有显著的闭合效应; 在对数据进行统计学分析之前, 需要对数据进行对数比(ilr)变换。经过对比, 对数比转换后的地球化学数据相比原始数据及对数变换后的数据具有更稳定的空间分布及内部结构。

(2) 对研究区岩石地球化学数据(ilr变换)进行稳健主成分分析(RPCA), 识别出矿区与成矿作用有关的两类元素组合, 分别为以Cu-As-Sb-Co元素为代表的铜成矿元素矿化组合和以Pb-Zn-Ag-Au-Mo- Ba-Cd-Bi-Sn元素为代表的铅锌金银多金属元素矿化组合, 两组元素组合与矿床形成的喷气沉积及变质改造‒热液叠加活动阶段相吻合。

(3) 运用-能谱面积多重分形模型, 有效识别并分离研究区原生晕地球化学数据元素组合异常‒背景分布特征; 结合矿区地质情况, 共在研究区圈定Ⅰ类靶区两个、Ⅱ类靶区一个, 为矿区边部进一步找矿工作指明了方向。

致谢:本次研究工作在那不勒斯费德里科二世大学Stefano Albanese教授指导下完成, 野外样品采集及数据收集工作得到了新疆哈巴河阿舍勒铜业股份有限公司陈泽粟等相关领导和新疆维吾尔自治区地质矿产勘查开发局第四地质大队吴晓贵的大力支持; 此外, 两位匿名评审专家对本文提出了宝贵的修改意见, 作者在此一致表示诚挚的谢意。

陈健. 2019. EDA异常下限分析在地质找矿中的应用. 矿产勘查, 10(8): 1961–1966.

陈毓川, 叶庆同, 冯京. 1996. 阿舍勒铜锌成矿带成矿条件和成矿预测. 北京: 地质出版社: 5–142.

成秋明. 2000. 多维分形理论和地球化学元素分布规律. 地球科学, 25(3): 311–318.

成秋明. 2001a. 多重分形与地质统计学方法用于勘查地球化学异常空间结构和奇异性分析. 地球科学, 26(2): 161–166.

成秋明. 2001b. 空间自相似性与地球物理和地球化学场的分解方法. 地球物理学进展, 16(2): 8–17.

成秋明. 2003. 非线性矿床模型与非常规矿产资源评价. 地球科学, 28(4): 445–454.

成秋明. 2006a. 应用复杂性‒非线性理论开展成矿预测——奇异性理论‒广义自相似性‒分形谱系多重分形理论与应用. 矿床地质, 25(S1): 463–466.

成秋明. 2006b. 非线性成矿预测理论: 多重分形奇异性‒广义自相似性‒分形谱系模型与方法. 地球科学, 31(3): 337–348.

成秋明. 2007. 成矿过程奇异性与矿产预测定量化的新理论与新方法. 地学前缘, 14(5): 42–53.

成秋明. 2012. 覆盖区矿产综合预测思路与方法. 地球科学, 37(6): 1109–1125.

成秋明, 张生元, 左仁广, 陈志军, 谢淑云, 夏庆霖, 徐德义, 姚凌青. 2009a. 多重分形滤波方法和地球化学信息提取技术研究与进展. 地学前缘, 16(2): 185–198.

成秋明, 赵鹏大, 陈建国, 夏庆霖, 陈志军, 张生元, 徐德义, 谢淑云, 王文磊. 2009b. 奇异性理论在个旧锡铜矿产资源预测中的应用: 成矿弱信息提取和复合信息分解. 地球科学, 34(2): 232–242.

龚庆杰, 张德会, 韩东昱. 2001. 一种确定地球化学异常下限的简便方法. 地质地球化学, 29(3): 215–220.

何旺, 罗先熔, 欧阳菲, 刘攀峰, 苏艺怀, 黄文斌, 王东, 游军, 张小明. 2020. 地电化学在陕西略阳县何家垭地区寻找隐伏铜镍矿的研究. 物探与化探, 44(3): 523–532.

胡以铿. 1991. 地球化学中的多元分析. 武汉: 中国地质大学出版社: 1–6.

李长江, 麻土华, 朱兴盛, 胡永和, 赵乃良. 1999. 矿产勘查中的分形、混沌与ANN. 北京: 地质出版社: 25–30.

李志纯. 1996. 阿尔泰左型雁列式火山‒沉积盆地形成、演化及成矿活动追踪. 大地构造与成矿学, 20(3): 189–200.

马艳芳. 2016. 双标图及其在成分数据中的应用. 山西: 山西大学硕士学位论文: 1–9.

韦导忠, 李晓晖, 周杰, 袁峰, 胡训宇, 杨迪, 李现琐. 2018. 基于S-A多重分形滤波方法的深层土壤Au元素异常识别——以皖东张八岭–管店地区为例. 地质学刊, 42(3): 407–411.

吴玉峰, 杨富全, 刘锋, 周明, 陈红琦. 2015. 新疆阿舍勒铜锌矿区脆韧性剪切带中绢云母40Ar/39Ar年代学及其地质意义. 地球学报, 36(1): 121–126.

新疆地质矿产开发局第四地质大队. 2010. 新疆阿尔泰哈巴河火山盆地阿舍勒铜锌矿区地质图.

杨富全, 李凤鸣, 秦纪华, 郑开平, 刘锋. 2013. 新疆阿舍勒铜锌矿区(潜)火山岩LA-MC-ICP-MS锆石U-Pb年龄及其地质意义. 矿床地质, 32(5): 869–883.

杨富全, 吴玉峰, 杨俊杰, 郑佳浩. 2016. 新疆阿尔泰阿舍勒矿集区铜多金属矿床模型. 大地构造与成矿学, 40(4): 701–715.

叶庆同, 傅旭杰, 王保良. 1998. 新疆阿尔泰山南缘多金属成矿带的成矿规律. 地质学报, 72(4): 3–5.

张俊杨, 杨晓芳, 李鑫林, 刘晗, 杨洋, 林健. 2016. 新疆哈巴河县阿舍勒铜矿一号铜锌矿床补充勘探报告. 厦门: 紫金矿业集团股份有限公司矿产地质勘查院: 15–66.

郑义, 李登峰, 张莉, 王成明, 方京. 2015. 新疆阿舍勒VMS型铜锌矿床元素活化富集作用初步研究. 大地构造与成矿学, 39(3): 542–553.

Afzal P, Alghalandis Y F, Khakzad A, Moarefvand P, Omran N R. 2011. Delineation of mineralization zones in porphyry Cu deposits by fractal concentration-volume modeling., 108(3): 220–232.

Ahrens L H. 1954. The lognormal distribution of the elements (A fundamental law of geochemistry and its subsidiary)., 5(2): 49–73.

Aitchison J. 1982. The statistical analysis of compositional data.:(), 44(2): 139–160.

Aitchison J, Greenacre M. 2002. Biplots of composi­tional data.:(), 51(4): 375–392.

Albanese S, De Vivo B, Lima A, Cicchella D. 2007. Geochemical background and baseline values of toxic elements in stream sediments of Campania region (Italy)., 93(1): 21–34.

Bölviken B, Stokke P R, Feder J, Jössang T. 1992. The fractal nature of geochemical landscapes., 43(2): 91–109.

Carlos M S J, Palarea A J, Martin F J A, Martinez S M, Vicente G M J. 2010. Sedimentary chemofacies characterization by means of multivariate analysis., 228(3–4): 218–228.

Cheng Q M. 1999. Multifractality and spatial statistics., 25(9): 949–961.

Cheng Q M. 2008. Modeling local scaling properties for multiscale mapping., 7(2): 525–532.

Cheng Q M, Agterberg F P, Ballantyne S B. 1994. The separation of geochemical anomalies from background by fractal methods., 51(2): 109–130.

Cheng Q M, Agterberg F P, Bonham-Carter G F. 1996. A spatial analysis method for geochemical anomaly separa­tion., 56(3): 183–195.

Cheng Q M, Bonham-Carter G F, Raines G L. 2001. GeoDAS: A new GIS system for spatial analysis of geochemical data sets for mineral exploration and environmental assessment. The 20th International Geochemical Exploration Symposium (IGES), Santiago de Chile: 42–43.

Cheng Q M, Xu Y G, Grunsky E. 2000. Integrated spatial and spectrum method for geochemical anomaly sepa­ration., 9: 43–52.

Claude J, Gre A, Eric L. 1995. Scaling laws and geoche­mical distributions., 132(1–4): 1–13.

Drew L J, Grunsky E C, David M S, Woodruff L G. 2010. Multivariate analysis of the geochemistry and mineralogy of soils along two continental-scale transects in North America., 409(1): 218–227.

Egozcue J J, Pawlowsky-Glahn V, Mateu-Figueras G, Barcelo-Vidal C. 2003. Isometric logratio transforma­tions for compositional data analysis., 35(3): 279–300.

Filzmoser P, Hron K, Templ M. 2018. Applied Compo­sitional Data Analysis (With work examples in R). Swit­zer­land: Springer International Publishing: 1–69.

Gabriel K R. 1971. The biplot graphic display of matrices with application to principal component analysis., 58(3): 453–467.

Hampel F R. 1974. The influence curve and its role in robust estimation., 69(346): 383–393.

Leys C, Ley C, Klein O, Bernard P, Licata L. 2013. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median., 49(4): 764– 766.

Li C J, Ma T H, Shi J F. 2003. Application of a fractal method relating concentrations and distances for separa­tion of geochemical anomalies from background., 77(2–3): 167–175.

Lima A, Albanese S, Cicchella D. 2005. Geochemical baselines for the radioelements K, U, and Th in the Campania region, Italy: A comparison of stream-sediment geochemistry and gamma-ray surveys., 20(3): 611–625.

Lima A, De Vivo B, Cicchella D, Cortini M, Albanese S. 2003.Multifractal IDW interpolation and fractal filtering method in environmental studies: An application on regional stream sediments of (Italy), Campania region., 18(12): 1853–1865.

Lima A, Plant J A, De Vivo B, Tarvainen T, Albanese S, Cicchella D. 2008. Interpolation methods for geoche­mical maps: A comparative study using arsenic data from European stream waters., 8(1): 41–48.

Lin X, Wang X Q, Zhou J, Chi Q H, Nie L S, Zhang B M, Xu S F, Zhao S D, Liu H L, Sun B B, Han Z X, Liu D S, Wang W, Liu Q Q, Bai J F, Fan H, Ma N, Zhang L S, Xu G Z, Wei W T, Zhao B, Shen W J. 2019. Concen­trations, variations and distribution of molybdenum (Mo) in catchment outlet sediments of China: Conclu­sions from the China geochemical baselines project., 103: 50–58.

Liu X C, Wang W L, Pei Y R, Yu P P. 2020. A knowledge- driven way to interpret the isometric log-ratio transfor­mation and mixture distributions of geochemical data., 210: 1–9.

Liu Y, Carranza E J M, Zhou K F, Xia Q L. 2019b. Compositional balance analysis: An elegant method of geochemical pattern recognition and anomaly mapping for mineral exploration., 28(4): 1269–1283.

Liu Y P, Zhu L X, Ma S M, Guo F S, Gong Q L, Tang S X, Gnanachandrasamy G, Zhou Y Z. 2019a. Cons­trai­ning the distribution of elements and their controlling factors in the Zhaojikou Pb-Zn ore deposit, SE China, via fractal and compositional data analysis., 108: 1–10.

Lloyd C D, Pawlowsky-Glahn V, Egozcue J J. 2012. Compositional data analysis in population studies., 102(6): 1251–1266.

Mandelbrot B B. 1983. The fractal geometry of nature., 51(3): 286.

Pawlowsky-Glahn V, Egozcue J J. 2006. Compositional data and their analysis: An introduction.,,, 264(1): 1–10.

Reimann C, Filzmoser P, Garrett R, Dutter R. 2011. StatisticalData Analysis Explained: Applied Environmental Statistics with R. New Jersey: John Wiley & Sons: 15–69.

Wang J, Zuo R G, Caers J. 2017. Discovering geochemical patterns by factor-based cluster analysis., 181: 106–115.

Zheng C J, Liu P F, Luo X R, Wen M L, Huang W B, Liu G, Wu X G, Chen Z S, Albanese S. 2021. Application of compositional data analysis in geochemical exploration for concealed deposits: A case study of Ashele copper- zinc deposit, Xinjiang, China., 130: 1–13.

Zheng C J, Luo X R, Wen M L, Ebrahimi P, Liu P F, Liu G, Li H P, Wei C C, Chen Z S, Albanese S. 2020. Axial primary halo characterization and deep orebody prediction in the Ashele copper-zinc deposit, Xinjiang, NW China., 213: 1–16.

Zuo R G. 2011. Identifying geochemical anomalies associated with Cu and Pb-Zn skarn mineralization using principal component analysis and spectrum-area fractal modeling in the Gangdese Belt, Tibet (China)., 111(1): 13–22.

Zuo R G. 2016b. Identifying geochemical anomalies associated with Sb-Au-Pb-Zn-Ag mineralization in North Himalaya, southern Tibet., 73: 1–12.

Zuo R G, Carranza E J M, Cheng Q M. 2012. Fractal/ multifractal modelling of geochemical exploration data., 122: 1–3.

Zuo R G, Wang J. 2016a. Fractal/multifractal modeling of geochemical data: A review.. 164: 33–41.

Zuo R G, Wang J. 2020. ArcFractal: An ArcGIS Add-In for processing geoscience data using fractal/multifractal models., 29(1): 3–12.

Zuo R G, Xia Q L, Wang H C. 2013. Compositional data analysis in the study of integrated geochemical anomalies associated with mineralization., 28: 202–211.

Rock Geochemical Data Mining and Weak Geochemical Anomaly Identification — A Case Study of the Ashele Copper-Zinc Deposit, Xinjiang, NW China

ZHENG Chaojie1, LIU Panfeng1, 2, LUO Xianrong1*, WEN Meilan1, HUANG Wenbin3, LIU Gang4, WU Xiaogui5, QIU Wei6, CHEN Zesu7, XIAO Hui7, WEI Chaocheng7

(1.College of Earth Sciences, Guilin University of Technology, Guilin 541006, Guangxi, China; 2. Collage of Environ­mental Science and Engineering, Guilin University of Technology, Guilin 541006, Guangxi, China; 3. Guangxi Branch of China National Geological Exploration Center of Building Materials Industry, Guilin 541002, Guangxi, China; 4. Geological Bureau of Ningxia Hui Autonomous Region, Yinchuan 750021, Ningxia, China; 5. Xinjiang Bureau of Geology and Mineral Exploration and Development, Urumqi 830000, Xinjiang, China; 6. Qinghai Geological Survey Institute, Xining 810012, Qinghai, China; 7.Xinjiang Habahe Ashele Copper Co., Ltd., Altay 836700, Xinjiang, China)

The priority of geochemical exploration prospecting is to correctly interpret the geochemical data in order to accurately extract the abnormal information associated with mineralization from the jumbled geological information, and to guide the prospecting research. However, geochemical data are compositional data with closure effect, therefore, to reveal the true spatial distribution of elements, the data should be pretreated with logratio transformation prior to multivariate analysis. In this paper, a total of 1009 surface primary halo samples, which were analyzed for 13 elements, were collected from the southern periphery of the Ashele copper-zinc deposit. The EDA technology is applied to process the raw, logarithmically transformed and logratio (ilr) transformed datasets respectively to explore the spatial scale distribution, and the internal structural characteristics of the different datasets are compared. Then, the correlation between element assemblage and metallogenic information indicated by the different datasets is interpreted by principal component biplots and score map which both are obtained from the (robust) principal component analysis. After that, the multifractal filtering technique (S-A model) is dedicated to decompose the mixed geochemical field and to delineate geochemical anomalies with robust principal component score data based on ilr transform. The result shows that: 1) the spatial scale of the logarithmically and logratio transformed dataset is more uniform than that of the raw data, and both transformed datasets approximately present a normal distribution; 2) the biplot of different datasets shows that only the ilr transformed data eliminates the “closure effect” and its first principal component reveals the element assemblage of the copper mineralization and the lead-zinc polymetallic mineralization in the study area. The score maps based on logarithmically and ilr transformation show that the high score area of the ilr transformed data can better reveal the geological prospecting information in the study area; 3) combining the geological prospecting information, the favorable element assemblage anomaly, and the background spatial distribution characteristics of the study area, three favorable prospecting targets are finally delineated.

compositional data analysis; multifractal technology; peripheral orebody prediction; Ashele district

2020-09-27;

2020-10-29;

2021-06-08

国家重点研发项目“华南热液型铀矿基地深部探测技术示范”(2017YFC0602600)及青海省科学技术厅应用基础研究计划项目(2018-ZJ-779)联合资助。

郑超杰(1993–), 男, 博士研究生, 勘查地球化学专业。E-mail: zcj@glut.edu.cn

罗先熔(1953–), 男, 教授, 博士生导师, 从事地球化学方面研究。E-mail: lxr811@glut.edu.cn

P632+.2

A

1001-1552(2022)01-0086-016