一种三点法求隐伏活动断层产状的计算方法

贺为民

一种三点法求隐伏活动断层产状的计算方法

贺为民

(中国地震局 地球物理勘探中心, 河南 郑州 450002)

求解三点问题的传统方法是作图法。目前缺乏利用初等几何学求解三点问题的完整计算方法。本次研究基于三点法的原理, 利用初等几何学知识推导了求断层面倾角、倾向和走向的计算公式。断层面倾角计算公式是以已知三点之间水平距离和三点之间高差为变量的代数表达式。断层面倾向或走向计算公式是以已知三点之间水平距离、三点之间高差和三点连线的方位角为变量的代数表达式。利用这些新公式易于编制计算程序。应用三点法求隐伏活动断层面产状的具体步骤为: ①通过改进的钻孔联合地质剖面, 取得断层面上已知三点的空间位置数据; ②依据已知三点的彼此高度关系条件, 选择断层面倾角和辅助角计算公式, 计算倾角、辅助角; ③依据已知三点的彼此空间位置关系条件, 选择断层面倾向和走向计算公式, 计算倾向和走向。以扣马断层为例, 采用上述新公式计算获得的扣马断层面的倾角、倾向和走向, 与采用地质罗盘在探槽中测量的断层面的倾角、倾向和走向结果比较一致。

三点问题; 产状; 隐伏活动断层; 钻孔探测; 钻孔联合地质剖面; 扣马断层

0 引 言

活动断层的产状是活动断层探测(中国地震局, 2009)和活动断层填图(中国地震局, 2014)的主要内容之一, 是开展活动断层危害性评价的重要资料, 是确定活动断层避让距离(徐锡伟等, 2002; 张建毅等, 2012)和制定工程抗断措施的重要依据。在隐伏活动断层探测中, 浅层地震勘探和钻孔探测是最有效的途径, 发挥着关键作用(汪一鹏, 2004; 邓起东等, 2007), 取得了丰富的成果(杨晓平等, 2007; 袁道阳等, 2008; 刘保金等, 2009; 张鹏等, 2015; 许汉刚等, 2016; 许良鑫等, 2019)。目前, 浅层地震勘探测线是尽可能垂直隐伏活动断层走向布设的单条测线, 钻孔探测测线常规布设方式是沿着浅层地震勘探测线布设的单条测线; 由于探测前常常难以准确确定隐伏活动断层的走向, 难以真正做到使上述测线垂直于隐伏断层的走向, 因此使得探测出的隐伏活动断层的倾向和倾角等产状成果一般为视倾向和视倾角, 仅少量钻孔探测成果(钻孔联合地质剖面)中钻遇断层面并采集到“楔状岩心”时才能够确定断层的(真)倾角(柴炽章等, 2006; 张世民等, 2007; 胡平等, 2010; 杨晓平等, 2011; 张鹏等, 2019)。为了求得隐伏活动断层的产状, 笔者对钻孔探测中的钻孔常规布设方式进行了改进, 当在钻孔常规布设方式下有2个钻孔钻遇同一个断层面时, 可在这2个钻孔连线之外(左侧或右侧)再布置1个钻孔; 当呈三角形分布的3个钻孔钻遇同一个断层面时, 就可以采用三点法求断层面的产状, 即(真)倾角、(真)倾向、(真)走向。三点法求解构造面(含断层面)产状的传统方法是作图法(朱志澄, 1999; 刘志宏等, 2011), 该方法已广泛应用, 但存在人工绘图过程中产生的测量图形长度和角度时产生的误差; 当数据量较大时,费时又费力。西村嘉四郎(1981)介绍了三点法求构造面倾角正切值的代数表达式(缺少倾向和走向计算式), 但表达式中求三角形之边长所需要的角度仍然为未知变量(需要由作图法求得)。董兆岗(2000)将三点法中最高点与中间高度点、最高点与最低点之间的连线作为构造面上的两条倾伏线(视倾斜线), 利用视倾角与(真)倾角之间的换算公式建立了三角函数方程组, 推导出了构造面倾向和倾角的反正切函数表达式, 计算过程中需要依据三点在水平面上的坐标关系, 利用“倾伏向修正值表”对两条倾伏线的倾伏向进行修正, 其倾向和倾角计算结果需要代入原方程进行检验。Hanerberg (1990)介绍了基于矢量分析和拉格朗日插值法求解三点问题的倾角和走向的矩阵表达式(缺少倾向计算式)。Ragan (2009)阐述了基于矢量分析, 以已知三点空间直角坐标为变量, 求解倾角和“倾向”(这里“倾向”指倾斜矢量与正东方向的夹角)的代数表达式。Fienen (2005)基于矢量分析和最小二乘法, 推导了已知多点(多于三点)时, 求解构造面倾角和走向的矩阵表达式(缺少倾向计算式)。因此, 目前仍然缺乏利用初等几何学求解三点问题的完整计算方法。为了提高隐伏活动断层产状的探测精度, 笔者利用初等几何学和三角函数知识, 推导了一套三点法求解断层面倾角、倾向和走向的代数表达式, 并在求解扣马断层(隐伏活动断层)产状中得到应用和验证。

1 三点法求断层面产状计算公式推导

三点法求解断层面产状的前提条件是: ①已知位于同一个断层面上且不在同一条直线上的三点位置(地理坐标或三点彼此间的水平距离及彼此连线的方位角)、高程(标高或彼此高差); ②在三点范围内断层面为同一个平面(朱志澄, 1999; 刘志宏等, 2011)。

设断层面为一个平面,为断层面的倾角(°), 点、、是断层面上不在同一条直线上的已知三点(点、、组成Δ, 采用Δ代表断层面), 点为最高点, 点为中间高度点、点为最低点,h为点与点之间的高差(m),h为点与点之间的高差(m),为点与点之间的水平距离(m),为点与点之间的水平距离(m),为点与点之间的水平距离(m), 见图1a～d、图1k～l。

依据点、、彼此高度关系可分为四种情况: ①三点高度皆不相等(点高于点, 且点高于点); ②一点高于等高另两点(点高于高度相等的点和点); ③一点低于等高另两点(点低于高度相等的点和点); ④三点等高。前三种情况下, 断层面为一个倾斜面, 是本文探讨的内容; 最后一种情况下, 断层面的空间位态显然为一个与已知三点高度(程)相同的水平面, 倾角为0°。

1.1 三点高度皆不相等时倾角计算公式

如图1a～b(西村嘉四郎, 1981, 有较大修改)所示, 在上述断层面上, 当点、、的高度皆不相等即h>h>0时, 直线上点、之间必然存在一点, 使点与点高度相等, 则直线为断层面的一条走向线; 过点作//交直线延长线于点, 过点作⊥交于点, 则直线、为断层面的倾斜线。

过直线作水平面(见图1a～d)。在水平面上, 点、、、分别为点、、、的投影, 则线段的长度为h,和的长度为h。在Δ中,的边长等于,的长边等于,的边长等于。

由于直线、分别是倾斜线、在水平面上的投影线即倾向线, 依据倾角的定义(刘志宏等, 2011), 则∠为断层面的倾角,∈(0°, 90°)(下同), ∠=∠, 且有⊥,⊥。在直角Δ中, 有:

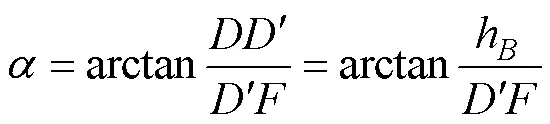
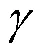
因为Δ∽Δ, 所以:

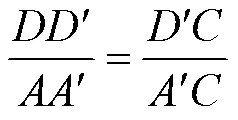
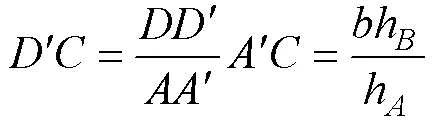
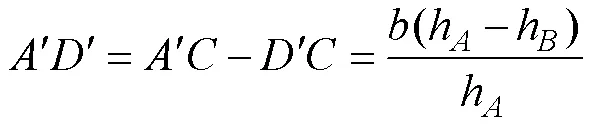
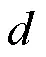
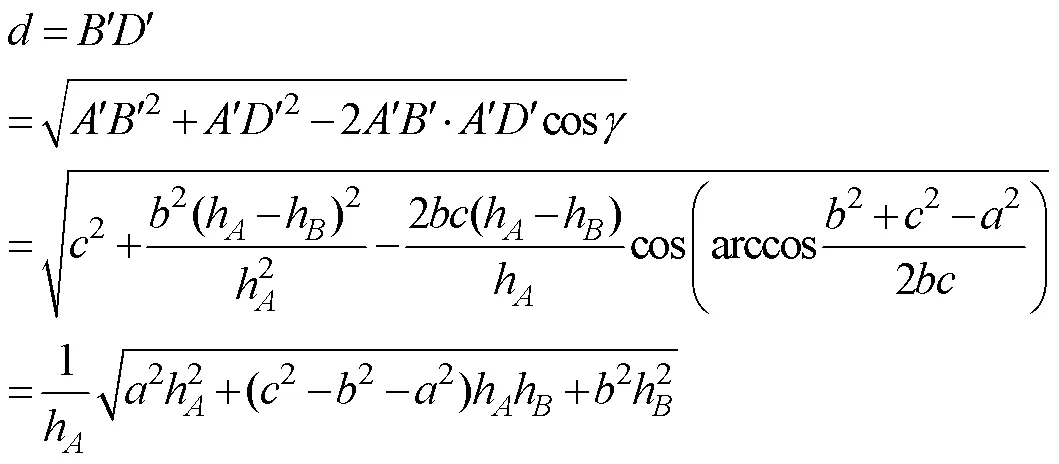
在Δ中, 令∠=, 称也为辅助角,∈(0°, 180°), 由正弦定理(韩昆和张宇, 2010)得:

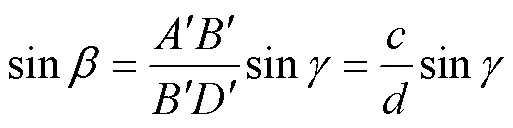
因为//,//, 所以//, ∠=∠=。在直角Δ中, 有:

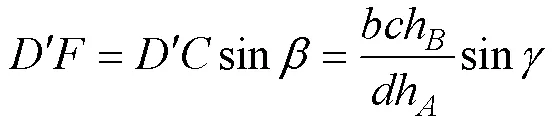
将公式(9)代入公式(1), 可得断层面的倾角的计算公式为:

由上述推导过程及结果可知, 断层面的倾角以及辅助角、的计算公式仅与点、、的彼此水平距离和高差有关, 是以三点彼此水平距离和高差为变量的代数表达式, 而与断层面的方位数据(走向或倾向)无关; 中间高度点无论位于Δ中边的右侧(图1a)还是左侧(图1b), 其断层面的倾角、辅助角、的计算公式相同。

1.2 三点高度皆不相等时走向和倾向计算公式

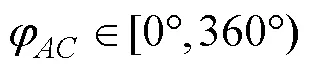
在断层面上, 由已知三点、、构成的Δ的形状及其在空间的分布具有多样性。从推导断层面的走向(记为, 下同)和倾向(记为, 下同)计算公式的需要出发, 从点位于边上端(相当于位于边上端)的角度来看(下同), Δ中的中间高度点与边的位置关系(相当于Δ中的点与边的位置关系)可以分为两类。第一类是中间高度点位于Δ的边的右侧(如图1a、k～l)(相当于点位于Δ的边的右侧(如图1a、c、e～l)), 为方便编写计算程序, 此时用不等式表达为:φ≥时,φ>φ, 或0°≤φ<时,φ<φ(基于下列分析后综合得出的结果)。以图1e、1g为例, 过点作//交直线于点, 直线前进方向的方位角等于直线前进方向的方位角, 等于φ。当指北方向线与重合时,φ=0°,φ=, φ>φ。当指北方向线与重合时,φ=0°,φ<φ。当指北方向线位于以点为原点从(不含)依顺时针方向到(不含)所构成的∠之内时(图1e),φ>,φ>φ。当指北方向线位于以点为原点从(不含)依顺时针方向到(不含)所构成的∠之内时(图1g),φ<,φ<φ。第二类是中间高度点位于Δ的边的左侧(图1b)(相当于点位于Δ的边的左侧(图1b、1d)), 此时用不等式表达为:φ≥时,φ<φ, 或0°≤φ<时,φ>φ。

1.2.1 走向计算公式推导

以“中间高度点位于Δ的边的右侧, 即φ≥时,φ>φ; 或0°≤φ<时,φ<φ”的条件为例, 推导以φ、为变量的断层面的走向φ的计算公式。

如图1e、f所示, 在水平面上,与前进方向的方位角相等, 为φ; 延长直线至点, 直线、与前进方向的方位角相等, 为φ, 是断层面的一个走向值。为求走向φ的需要, 将φ与辅助角的关系分为两种情况: ①0°≤φ<360°–; ②360°–≤φ<360°。

当0°≤φ<360°–时, 指北方向线位于以点为原点从(不含)依顺时针方向到(含)所构成的∠之内, 如图1e所示, 有:

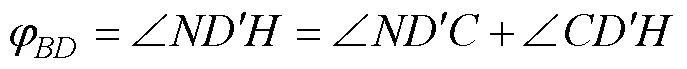
因为, ∠=φ(下同), ∠=∠′′′=(下同), 代入式(11), 可得走向φ计算式:

φ=φ+β(12)

当360°–≤φ<360°时, 指北方向线位于以点为原点从(不含)依顺时针方向到(含)所构成的∠之内, 如图1f所示, 有:

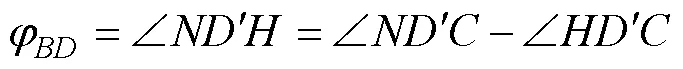
因为, ∠=360°–∠, 代入公式(13), 可得走向φ计算式:

φ=φ+–360° (14)

公式(11)～(14)中, ∠、∠、∠、∠、∠、∠分别为以点为原点从、、、、、依顺时针方向到、、、、、所构成的角。

每条走向线有两个走向值, 两者相差180°(刘志宏等, 2011)。本文仅给出其中一个走向的计算式, 另一个不再赘述。

类似地, 还推导了“中间高度点位于Δ的边的左侧, 即φ≥时;φ<φ; 或0°≤φ<时,φ>φ”的条件下断层面的走向φ的计算公式, 见表1中公式(15)、(16)。

表1 断层面走向计算公式

可见, 在已知三点、、的高度皆不相等时, 断层面的走向不仅与已知三点的彼此水平距离和高差有关, 还与已知三点的彼此位置关系、彼此连线方位角有关。

1.2.2 倾向计算公式推导

为了推导倾向计算公式的需要, 将辅助角分为直角(=90°)、锐角(0°<<90°)和钝角(90°<<180°)三种情况。

仍然以“中间高度点位于Δ的边的右侧, 即φ≥时,φ>φ; 或0°≤φ<时,φ<φ”的条件为例, 推导以φ、为变量的断层面的倾向φ计算公式。

如图1e～j所示, 在水平面上,前进方向的方位角为φ, 直线前进方向的方位角等于φ, 倾向φ为倾向线前进方向的方位角; 为了求倾向φ的需要, 当辅助角为锐角时, 将φ与辅助角的关系分为两种情况: ①0°≤φ<90°–;②90°–≤φ<360°。当辅助角为钝角时, 将φ与辅助角的关系分为3种情况: ①0°≤φ<360°–; ②360°–≤φ<450°–; ③450°–≤φ<360°。

当辅助角为锐角(0°<<90°)和0°≤φ<90°–时,位于从(不含)依顺时针方向到(含)所构成的∠之内, 如图1g所示, 有:

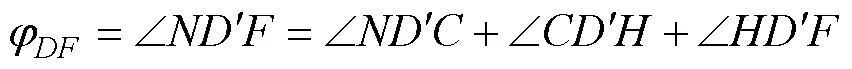
因为, ∠=270°, 代入公式(17), 得倾向计算式:

φ=++ 270° (18)

当辅助角为锐角(0°<<90°)和90°–≤< 360°时, 指北方向线位于从(不含)依顺时针方向到(含)所构成的∠之内, 如图1e所示, 有:

因为, ∠=90°(下同), 代入公式(19), 得倾向φ计算式:

φ=φ+– 90° (20)

当辅助角为钝角(90°<<180°)和0°≤φ< 360°–时, 指北方向线位于从(不含)依顺时针方向到(含)所构成的∠之内, 如图1h所示, 有:

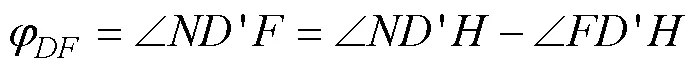
因为, ∠=∠+∠, 代入公式(21), 得倾向φ计算式:

φ=φ+– 90° (22)

当辅助角为钝角(90°<<180°)和360°–≤φ<450°–时, 指北方向线位于从(不含)依顺时针方向到(含)所构成的∠之内, 如图1i所示, 有:

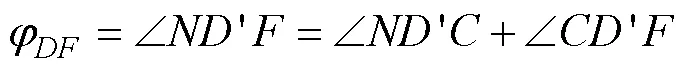
因为, ∠=∠– 90°, 代入公式(23), 得倾向φ计算式:

φ=φ+– 90° (24)

公式(22)、(24)具有相同的最终表达式, 可将公式(22)、(24)的适用条件合并为: 90°<<180°和0°≤φ<450°–。

当辅助角为钝角(90°<<180°)和450°–≤φ<360°时, 指北方向线位于从(不含)依顺时针方向到(含)所构成的∠之内, 如图1j所示, 有:

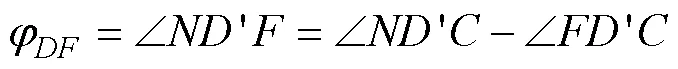
因∠=∠∠, ∠=270°, ∠=180°–∠, 代入公式(25), 得倾向φ公式:

φ=φ+– 45° (26)

公式(17)～(26)中, ∠、∠、∠、∠、∠、∠、∠、∠、∠、∠分别为以点为原点从、、、、、、、、、依顺时针方向到、、、、、、、、、所构成的角。

当辅助角为直角即=90°时,⊥,是断层面的一条倾向线, 断层面的倾向φ等于前进方向的方位角φ, 即:

φ=φ(27)

公式(27)也适用于“中间高度点位于Δ的边的左侧”的情况。

类似地, 还推导了在“中间高度点位于Δ的边的左侧, 即φ≥时,φ<φ, 或0°≤φ<时,φ>φ”的条件下断层面的倾向φ的计算公式, 见表2中公式(28)、(29)、(30)、(31)。

可见, 断层面的倾向不仅与已知三点的彼此水平距离和高差有关, 还与已知三点的彼此位置关系、彼此连线方位角有关。

1.3 一点高于等高另两点时产状计算公式

如图1k所示, 在断层面上, 当最高点高于高度相等的点(视为中间高度点)和点(视为最低点)即h>h=0时, 直线即为断层面的一条走向线。过直线作水平面, 点在水平面上的投影为点,的长度等于h, 过点作⊥交于点, 则直线为断层面的一条倾斜线, 点为点水平面上的投影,和为倾向线, 依据倾角的定义(刘志宏等, 2011), 则∠为断层面的倾角, ∠=∠。在直角Δ中, 有:

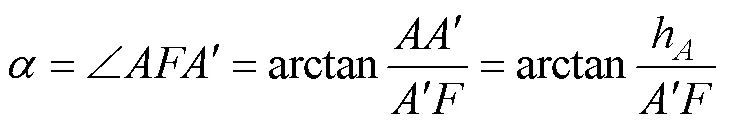
在Δ中,的边长等于,的长边等于,的边长等于,⊥, 则Δ的面积为:

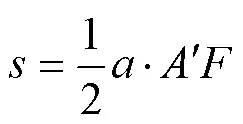
而由海伦公式(韩昆和张宇, 2010)亦可得Δ的面积为:

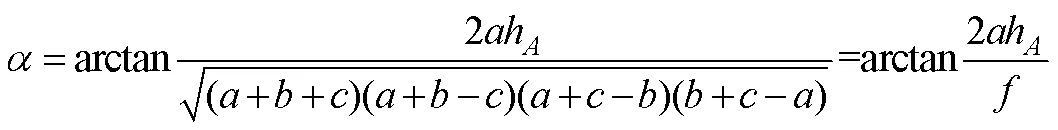
有趣的是, 将h=0代入公式(10), 也可以得到公式(35)。公式(35)可以看作是公式(10)的一个特例。

表2 断层面倾向计算公式

由公式(35)可知, 断层面的倾角与已知三点、、的彼此水平距离和高差有关, 而与断层面的方位数据(走向或倾向)无关。

依据走向和倾向的定义(刘志宏等, 2011), 走向线前进方向的方位角φ(°)为断层面的一个走向值(也列入表1)。倾向线前进方向的方位角为断层面的倾向, 记为φ(°)。依据走向与倾向之间的关系(刘志宏等, 2011), 也推导了由φ计算φ的公式(36)、(37)、(38)、(39), 见表2, 其中辅助角为图1k中的∠,的计算公式与公式(2)具有相同的代数表达式。

1.4 一点低于等高另两点时产状计算公式

如图1l所示, 在断层面上, 当最低点低于高度相等的点(视为最高点)和点(视为中间高度点)即h=h>0时,即为断层面的一条走向线。过点作水平面, 点、在水平面上的投影分别为点、, 过点作⊥交于点, 延长直线至点, 点、在水平面上的投影分别为点、, 则直线为断层面的一条倾斜线,和为倾向线, 依据倾角的定义(刘志宏等, 2011), 则∠为断层面的倾角, ∠=∠。采用1.3节的思路可得:

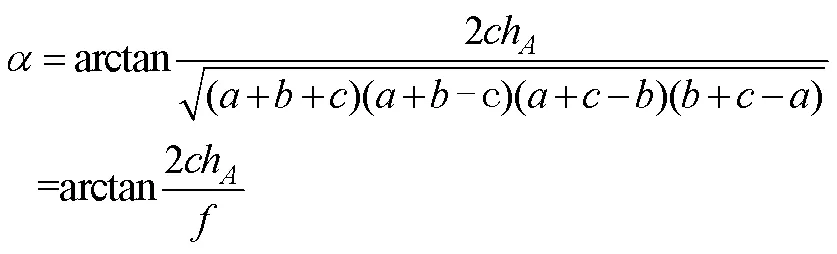
将h=h代入公式(10), 也可以得到公式(40)。公式(40)也可以看作是公式(10)的一个特例。

依据走向和倾向的定义(刘志宏等, 2011), 走向线前进方向的方位角φ(°)为断层面的一个走向值(表1)。倾向线F′C前进方向的方位角为断层面的倾向, 记为φ(°)。依据走向与倾向之间的关系(刘志宏等, 2011), 也推导了由φ计算φ的公式(41)、(42)、(43)、(44)(表2), 其中辅助角为图1l中的∠,的计算公式与公式(2)具有相同的代数表达式。

需要指出的时, 上述的产状计算公式是针对一个断层面而推导出的公式。当有个(为大于1的正整数)所求断层面时, 将这个断层面分别记为由点A、B、C组成的ΔABC, 其中, 点A为已知三点中的最高点, 点B为中间高度点, 点C为最低点,=1, 2, …,; 显然, 公式中的其他代数(字母)也应填加对应的下标。之后, 分别采用上述公式计算, 即可得到个所求断层面的产状。

1.5 产状计算公式应用步骤

上述产状计算公式特别是倾向计算公式先决判断条件较多, 为便于编写计算程序, 给出了产状计算流程图(图2), 并建议求隐伏断层面产状步骤如下。

(1) 通过钻探、测量等地质勘探获得隐伏断层面上已知三点、、的空间位置数据:h、h、、、、φ、φ、φ, 作为程序计算的输入数据(图2)。

(2) 根据已知三点、、彼此高度关系条件, 计算辅助角、和倾角。可以分为两种情况(图2): 如果h>h>0, 则由公式(2)计算, 由公式(8)计算, 由公式(10)计算; 否则(即如果h>h=0, 或者如果h=h>0时), 则由公式(2)计算, 由公式(10)计算。

(3) 根据已知三点、、的彼此高度、位置、方位角和辅助角关系条件, 可以分为三大类(即:h>h>0、h>h=0、h=h>0), 并进一步分为6小类计算走向(见表1、图2), 分为17小类计算倾向(见表2、图2)。

2 扣马断层隐伏断层面产状计算

2.1 扣马断层

扣马断层位于河南省孟津县扣马村南部, 在邙山北麓黄土边坡中下部呈近东西向展布, 倾向北, 为正断层。在地震地质调查工作中, 在扣马村南部多条黄土冲沟两侧的陡坎上(黄土梁边缘的陡坡上)发现了10个断层露头点。在这些断层露头点上, 断层切割的最新地层为晚更新世黄土, 断层上覆最老地层也是晚更新世黄土。因此, 扣马断层是一条活动断层, 其最新活动时代为晚更新世(贺为民, 2019)。

在其中一个断层露头点上开展了槽探工作。如图3所示, 探槽位于陡坎2之中, 探槽长8.0 m, 高8.4～8.8 m。如图4a所示, 探槽揭示的断层面清晰, 断层带宽度10～20 cm; 断层下盘(南盘)为早更新世黏土、砾石、细砂, 断层上盘(北盘)为晚更新世黄土。采用地质罗盘实测探槽中断层面产状为355°∠65°。陡坎1的地层为断层上覆最老地层(晚更新世黄土), 该层没有发现被断层断错或扰动的迹象。

2.2 扣马断层钻探与产状计算

为了求取该断层的下部产状, 在断层上盘(北盘)开展了钻孔探测, 并将钻孔布设在陡坎2(探槽)顶部的小平台上。为了确保不在同一条直线上的(即呈三角形分布的)三个钻孔探测到该断层面, 将7个钻孔布置为2排(图3), 单孔深度21.0～42.0 m。

图2 三点法计算隐伏断层面产状流程图

根据钻孔岩心的岩性特征, 结合年龄测试结果和区域地层对比分析, 编制了钻孔联合地质剖面, 见图4b。其中, 各个钻孔之间的水平距离为各个钻孔中心点在钻孔ZK8、ZK12中心点连线上的垂直投影点之间的水平距离。钻孔联合地质剖面探测结果表明, 钻孔ZK12、ZK8、ZK9、ZK7、ZK10钻遇了断层面。钻探揭露的断层下盘(南盘)地层皆为下更新统(U1卵石、U2细砂、U3黏土、U4细砂、U5黏土), 断层上盘(北盘)地层为下更新统(U6细砂、U7卵石、U8黏土)、中更新统(U9黄土夹古土壤、U10古土壤、U11黄土、U12古土壤)和上更新统(U13黄土)。钻孔ZK11下部揭露的U6细砂、U7卵石、U8黏土(图4b)与探槽南部从下至上的细砂、卵石、黏土(图4a)可视为同层位地层。断层上盘(北盘)地层层面不平整以及黄土层中存在(弱)古土壤透镜体与断层活动有关。

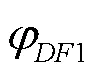
类似地, 由钻孔ZK9、ZK7、ZK10钻遇的断层面记为断层面Δ222(图4d)。由钻探和测量结果可知, 钻孔ZK9、ZK7、ZK10的中心线与Δ222的交点的高程分别为95.77 m、91.46 m、82.99 m; 显然, 在这三个交点中, 钻孔ZK9的中心线与Δ222的交点为最高点, 视为点2; 钻孔ZK7的中心线与Δ222的交点为中间高度点, 视为点2; 钻孔ZK10的中心线与Δ222的交点为最低点, 视为点2。将断层面Δ222由钻探、测量获得的数据和采用上述公式计算产状的结果也列于表3。

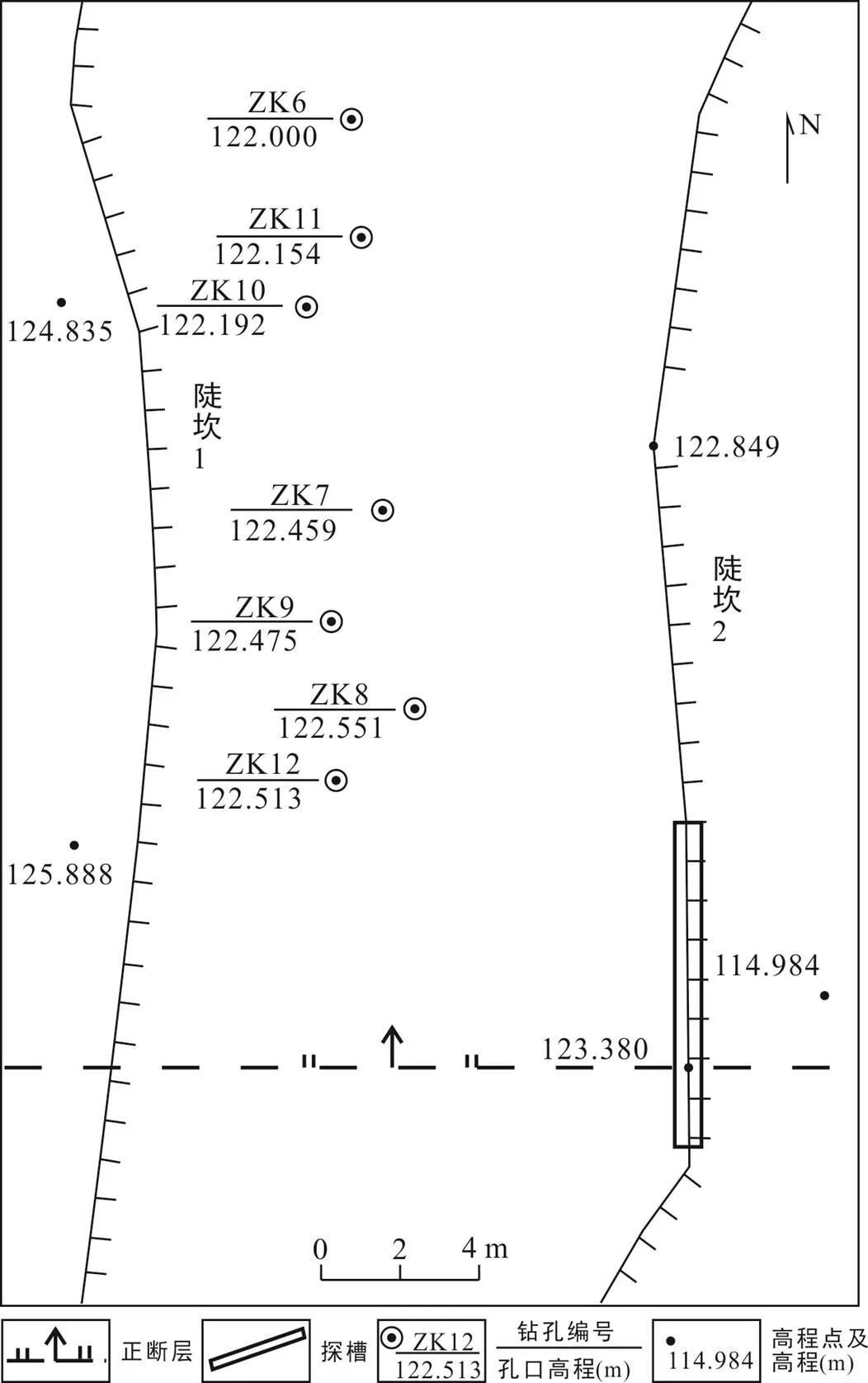
图3 扣马断层探槽和钻孔位置图

2.3 产状计算结果讨论

基于上述钻孔探测和断层面产状计算, 断层在钻孔ZK12、ZK9之间的隐伏段产状为2.55°∠68.76°, 在钻孔ZK9、ZK10之间的隐伏段产状为356.17° ∠57.96°, 与地质罗盘在探槽中测量的同一个断层面(不同部位)产状数据(355°∠65°)比较一致。

当然, 在探槽和钻孔中获得的断层产状数据也存在一些差异, 主要原因在于: ①在上述钻孔探测工作中, 虽然各个钻孔孔口之间的水平距离和方位角测量数据精度较高(Trimble-R8 GPS RTK测量精度为毫米级), 但是钻孔岩心及其分层深度(高程)数据的精度受钻探取心质量、现场地质编录人员的影响较大(贺为民, 2016); ②由于钻孔深度较浅, 本次未进行钻孔倾斜校正工作; ③断层面本身不是一个平面, 而是随空间位置起伏变化的曲面。

为了充分利用钻孔探测技术, 提高隐伏活动断层产状探测精度(从视倾角、视倾向提高到真倾角、真倾向), 针对需要探测的隐伏活动断层, 在浅层地震勘探的基础上, 选择在浅层地震反射时间剖面上显示清楚、有明显垂直位移、埋深较浅断层的上断点作为目标上断点。首先, 以目标上断点为中心, 采用钻孔常规布设方式即沿着浅层地震勘探测线或者大角度相交(甚至垂直)于断层走向布设钻孔探测测线(当有较详细的断层走向资料时), 开展隐伏断层精确定位和活动性鉴定等探测工作, 钻孔布置和施工宜采用对折法(雷启云等, 2011)。之后, 当有2个钻孔(记为ZKx、ZKy)钻遇同一个断层面时, 对钻孔常规布设和施工方式进行改进或补充, 即在这两个钻孔(ZKx、ZKy)连线附近(左侧或右侧)再布置1～2个钻孔(记为ZKu、ZKv), 使钻孔ZKx、ZKy、ZKu以及ZKx、ZKy、ZKv在水平面上呈三角形分布。当有三个呈三角形分布的钻孔例如钻孔ZKx、ZKy、ZKu钻遇同一个断层面时, 基于孔口高程(高差)、钻孔中心彼此水平距离、钻孔中心彼此连线方位角、钻遇的断层面埋深、钻孔倾斜度等测量数据, 分别计算钻孔ZKx、ZKy、ZKu中心线与钻遇断层面的三个交点(为断层面上已知三点)的高程(高差)、彼此水平距离、彼此连线方位角。之后, 应用上述公式计算可得隐伏活动断层的倾角、走向和倾向。

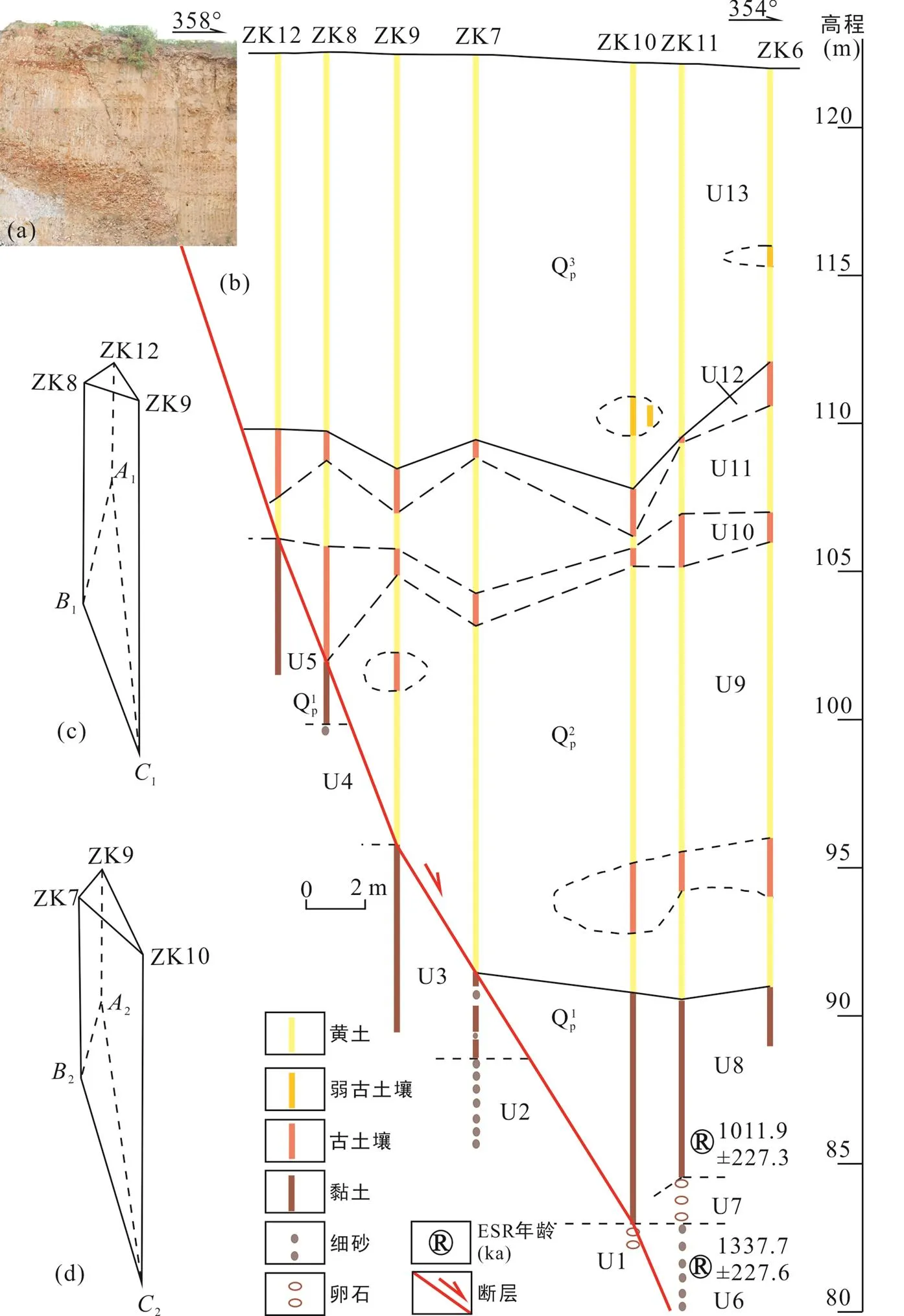
图4 扣马断层钻孔联合地质剖面及断层产状计算示意图

表3 扣马断层产状计算结果

上述断层面产状计算方法克服了传统的三点法中的作图法过程中由于人工作图和量图而产生的误差, 并且易于编程, 便于处理大批量数据。这些计算公式不但适用于隐伏活动断层面产状计算, 还适用于各类呈平面状地层(矿层、岩层)的产状计算。

3 结 论

(1) 本文基于三点法求断层面产状的原理, 利用初等几何学和三角函数知识系统地推导了三点法求断层面的(真)倾角、(真)倾向和(真)走向的计算公式, 断层面倾角计算公式是以已知三点之间水平距离和三点之间高差为变量的代数表达式。断层面倾向或走向计算公式是以已知三点之间水平距离、三点之间高差和三点连线的方位角为变量的代数表达式。这些新公式便于计算机编程和计算, 消除了传统的三点法之作图法求断层面产状时因人工作图和量图而产生的误差, 并提高了工作效率。

(2) 以扣马断层隐伏断层面产状探测为例, 采用上述倾角、倾向和走向计算公式, 计算了钻孔探测的同一个断层面的相邻两个部位的产状, 其结果为2.55°∠68.76°、356.17°∠57.96°, 与采用地质罗盘在探槽中测量的同一个断层面(不同部位)产状数据(355°∠65°)比较一致。提高钻孔取心质量和岩心分层深度数据的精度以及进行钻孔倾斜校正等可以提高隐伏活动断层面产状探测的精度。

(3) 隐伏活动断层产状探测计算可以分为三个步骤: ①基于改进的隐伏活动断层钻孔探测布孔方式(即改进的钻孔联合地质剖面), 求取断层面上已知三点彼此水平距离、高差和彼此连线的方位角; ②依据断层面上已知三点的彼此高度关系条件, 选择倾角、辅助角计算公式, 计算可得断层面的倾角、辅助角; ③依据断层面上已知三点的彼此高度关系、彼此水平位置关系、彼此连线的方位角、辅助角等条件, 选择断层面倾向、走向的计算公式, 计算可得断层面的倾向或走向。

(4) 利用三点法的原理推导出的倾角、倾向和走向的计算公式, 还适用于各类平面状地层(矿层、岩层)的产状计算。

致谢:衷心感谢中国地质大学(北京)王根厚教授和另一位匿名审稿专家对文章提出的宝贵修改意见。感谢同事卫蕾华、宋晓鹏、万森林、杨杰、张峰、莘海亮对槽探、钻探、绘图等工作的辛勤付出。

柴炽章, 孟广魁, 杜鹏, 王银, 刘保金, 沈卫华, 雷启云, 廖玉华, 赵成斌, 酆少英, 张谢辉, 谢晓峰. 2006. 隐伏活动断层的多层次综合探测——以银川隐伏活动断层为例. 地震地质, 28(4): 536–546.

邓起东, 卢造勋, 杨主恩. 2007. 城市活动断层探测和断层活动性评价问题. 地震地质, 29(2): 189–200.

董兆岗. 2000. 通过空间一平面内三点坐标计算该面产状. 云南地质, 19(3): 304–307.

韩昆, 张宇. 2010. 高中数学公式定律及要点透析. 沈阳: 辽宁教育出版社: 143–147.

贺为民. 2016. 地震工程地质条件勘测中钻探相关工作探讨. 世界地震工程, 32(4): 157–163.

贺为民. 2019. 洛阳市活断层探测与地震危险性评价项目子专题7目标断层的晚第四纪活动性鉴定成果报告. 郑州: 中国地震局地球物理勘探中心: 89–109.

胡平, 刘保金, 白立新, 母红旺, 张杰, 丁彦慧, 罗华春, 冯锐. 2010. 奥林匹克公园地区隐伏断裂综合探测. 地球物理学报, 53(6): 1486–1494.

雷启云, 柴炽章, 孟广魁, 杜鹏, 王银, 谢晓峰. 2011. 隐伏活断层钻孔联合剖面对折定位法. 地震地质, 33(1): 45–55.

刘保金, 胡平, 陈颙, 张先康, 酆少英, 杨晓平, 于慎鄂, 孟勇奇, 石金虎, 寇昆朋. 2009. 北京平原西北部地壳浅部结构和隐伏活动断裂——由地震反射剖面揭示. 地球物理学报, 52(8): 2015–2025.

刘志宏, 刘正宏, 梁一鸿, 徐仲元, 孙加鹏. 2011. 构造地质学(第二版). 北京: 地质出版社: 4–254.

汪一鹏. 2004. 关于“城市活断层探测与地震危险性评价工作大纲(试行)”的几点认识. 地震地质, 26(4): 559–565.

西村嘉四郎. 1981. 利用三点法测定走向和倾角. 国外地质勘探技术, (7): 17–22.

徐良鑫, 卞菊梅, 呼楠, 田勤虎, 田伟新, 段蕊. 2019. 骊山山前断裂华清池以西段晚更新世以来的活动性. 地震地质, 41(3): 561–575.

徐锡伟, 于贵华, 马文涛, 冉永康, 陈桂华, 韩竹军, 张兰凤, 尤惠川. 2002. 活断层地震地表破裂“避让带”宽度确定的依据与方法. 地震地质, 24(4): 470–483.

许汉刚, 范小平, 冉勇康, 顾勤平, 张鹏, 李丽梅, 赵启光, 王金艳. 2016. 郯庐断裂带宿迁段F5断裂浅层地震勘探新证据. 地震地质, 38(1): 31–43.

杨晓平, 袁洪克, 宋新初, 王里, 刘保金, 叶建青, 陈献程, 周本刚. 2011. 浙江宁波育王山山前隐伏断层勘探和新活动时代. 地球科学, 36(6): 967–976.

杨晓平, 郑荣章, 张兰凤, 陈献程, 马文涛, 徐锡伟, 王瑞光, 梁辉, 王琰. 2007. 浅层地震勘探资料地质解释过程中值得重视的问题. 地震地质, 29(2): 282–293.

袁道阳, 王兰民, 何文贵, 刘百篪, 葛伟鹏, 刘兴旺, 梁明剑, 郑文俊. 2008. 兰州市地震活断层探测新进展. 地震地质, 30(1): 236–249.

张建毅, 薄景山, 袁一凡, 黄静宜. 2012. 活动断层及其避让距离研究综述. 自然灾害学报, 21(2): 9–18.

张鹏, 李丽梅, 刘建达, 许汉刚, 李金良, 顾勤平, 蒋新. 2015. 徐州废黄河断裂的第四纪活动性. 地震地质, 37(1): 208–221.

张鹏, 张媛媛, 许汉刚, 刘建达, 陈建强, 李丽梅, 李金良, 顾勤平, 蒋新. 2019. 苏锡常断裂的第四纪活动性. 地震地质, 41(5): 1172–1184.

张世民, 王丹丹, 刘旭东, 任俊杰, 罗明辉, 张国宏, 赵国存, 王瑞, 张英礼. 2007. 北京南口‒孙河断裂带北段晚第四纪活动的层序地层学研究. 地震地质, 29(4): 729–743.

中国地震局. 2009. DB/T15-2009 活动断层探测. 北京: 地震出版社: 5–10.

中国地震局. 2014. DB/T53-2013 1︰50 000活动断层填图. 北京: 地震出版社: 3–7.

朱志澄. 1999. 构造地质学. 北京: 中国地质大学出版社: 219–220.

Fienen M N. 2005. The three-point problem, vector analysis and extension to the n-point problem., 53(3): 257–262.

Hanerberg W C. 1990. A Lagrangian interpolation method for three-point problems., 12(7): 945–947.

Ragan D M. 2009. Structural Geology, an Introduction to Geometrical Techniques (fourth edition). New York: Cambridge University Press: 157–164.

Three-point Method for Calculation of the Occurrence of Buried Active Fault

HE Weimin

(Geophysical Exploration Center, China Earthquake Administration, Zhengzhou 450002, Henan, China)

Graphing method is a traditional method for three-point problem. At present, there is no complete calculation method to solve three-point problem by elementary geometry. Based on the principle of three-point method, a few formulas derived from the knowledge of geometry and trigonometric function are proposed to calculate dip angle, dip, and strike of fault surface. The formulas used to calculate the dip angle of fault surface are the algebraic expressions, within which the horizontal distance and height difference between three known points are used as parameters. The formulas used to calculate dip or strike of fault surface are algebraic expressions that include parameters such as the horizontal distance and height difference as well as the azimuth of the line between the three known points. These new formulas are easy to programme. The steps to obstain the occurrence of buried active fault surface by using the three-point method are presented as follows. First, the spatial location data of the three known points on the fault surface is obtained from improved composite drilling geological section. Secondly, based on the height relationship of the three known points, the formulas are chosen to calculate the dip angle and the auxiliary angle of the fault surface. Thirdly, based on the spatial location relationship of the three known points, the formulas are chosen to calculate the dip and strike of the fault surface. Taking the Kouma fault as an example, the dip angle, dip, and strike of the Kouma fault surface are obtained by using these new formulas. In the prospecting trench, the dip angle, dip, and strike of the Kouma fault surface are measured by using geological compass. Both results of the dip angle, dip, and strike are quite consistent.

the three-point problem; occurrence; buried active fault; drilling; composite drilling geological section; Kouma fault

2020-07-30;

2020-10-03;

2021-02-01

中国地震局地震科技星火计划攻关项目(XH19060)和国家自然科学基金项目(41704058)联合资助。

贺为民(1965–), 男, 博士, 高级工程师, 从事地震地质、活动断层探测等方面的研究工作。E-mail: wmhe65@163.com

P542.3

A

1001-1552(2022)01-0036-012