复合Legendre方程边值问题解的相似结构法
2022-03-03李顺初邵东凤桂钦民
夏 星, 李顺初, 邵东凤, 桂钦民
(1.西华大学 理学院, 四川 成都 610039;2.北京东润科石油技术股份有限公司, 北京 100029)
0 引 言
微分方程是数学研究的重要内容之一[1-2],被广泛应用于油藏[3-5]、海洋声学[6]、电磁场[7]等领域,在实际生活中扮演着举足轻重的作用,那么微分方程的求解就显得尤为重要.很多学者都致力于研究微分方程的求解,并且有些学者在对微分方程边值问题的研究中发现了其解具有某种相似结构[8],某些定解问题的解均可用连分式来被表示,如:李顺初等[9-10]研究了复合Hermit方程边值问题和复合型Laguerre方程边值问题,冷礼辉等[11]研究了扩展变型Bessel方程边值问题,董晓旭[12]研究了三区复合型二阶齐次线性微分方程边值问题,刘爱华等[13]研究了二阶齐次微分方程边值问题,郑鹏社等[14]研究了一类非线性复合变型Bessel方程组的边值问题,这对于其求解过程的简化起着至关重要的作用,也促使微分方程边值问题的求解不断被完善.
Legendre方程在多个领域都有着广泛的应用,例如:物理学、生物学、天文学等[15],那么方程的求解对于解决实际问题就显得至关重要,但也是一项复杂烦琐的过程[16],那么有没有比较便捷的方法呢?近年来, 李顺初等[17-19]就此问题提出了新的思路,他们针对连带型Legendre方程的边值问题、复合连带型Legendre方程的边值问题、Legendre方程的边值问题等问题的解进行了研究,并发现了对应方程解的相似结构.本文基于他们的研究结果,对复合Legendre方程的边值问题进行了研究:
(1)
其中li(i=1,2),α,θ,β,λ,μ,e,f,G,H,Q均为实数,Q>0,β>α>0,G2+H2≠0,li(i=1,2)是正整数.
1 预备知识
引理1Legendre方程的通解为[15]:

其中Pli(x),Qli(x) 分别为Legendre多项式和第二类Legendre函数,C1,C2,C3,C4为任意常数,则

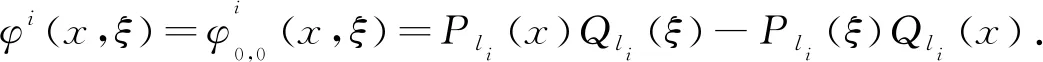
证明由 Legendre函数的微分性质[15],
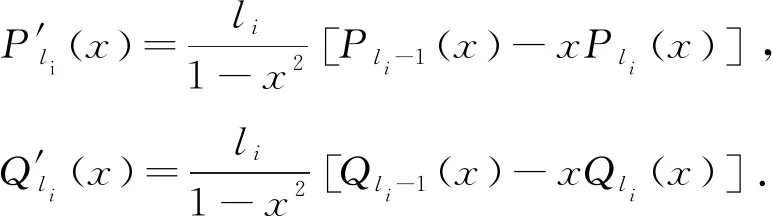
即有

同理可证其他式子.
2 主要定理及其证明
定理1对于复合Legendre方程的边值问题(1)(其中参数的限制与(1)中的相同)其有且仅有一个解,则其左区解(-1≤α (2) 其右区解(θ (3) 其中Φ*(x)是右相似核函数,即 (θ (4) Φ(x) 是左相似核函数,即 (-1≤α (5) 证明由引理1可得,边值问题(1)的左、右区通解分别是 y1=C1Pl1(x)+C2Ql1(x), 其中C1,C2,C3,C4是常数;Pli(·),Qli(·)分别为Legendre多项式和第二类Legendre函数且 根据边值问题(1)的左边界条件、交界点x=θ处两个衔接条件和右边界条件有 (6) C1Pl1(θ)+C2Ql1(θ)-C3λPl2(θ)- (7) (8) (9) 联立方程(6)(7)(8)(9)可求解得到C1,C2,C3,C4.因为边值问题(1)的解唯一,所以D≠0,结合引理2,计算可得 (10) (11) (12) (13) (14) 式(10)-(14)通过Cramer法则可得 从而对计算出的结果进行整理,我们便可得出在定解问题(1)中的左、右区解,即为式(2)和式(3). 综上可得到以下推论. 推论1假若复合Legendre方程边值问题(1)的右边界条件中y2(β)=0,(H=0,G≠0),那么右相似核函数为 推论2假若复合Legendre方程边值问题(1)中的右边界条件为y′2(β)=0,(G=0,H≠0) ,那么右相似核函数为 推论3在左端点,有 复合Legendre 方程边值问题求解的相似构造法步骤如下: Step4联立Q,e,f(左边界条件[ey1+(1+ef)y′1]|x=α=Q的系数)和Φ(x),解得边值问题. 综上,可总结出相似构造法在求解该类复合Legendre 方程边值问题(1)时简洁明了的流程图 ,如图1所示. 图1 相似构造法流程图 用以上介绍的相似构造法求解边值问题(如l1=1,l2=2,e=1,f=2,Q=1,G=1,H=2,α=-1,β=1,θ=0,λ=1,μ=1.) (15) 又用(1-x2)y″2-2xy′2+6y2=0,0 且 y1|x=0=y2|x=0,y′1|x=0=y′2|x=0的系数),构造左相似核函数 第四步利用Q=1,e=1,f=2(左边界条件[y1+3y′1]|x=-1=1的系数)和Φ(x),可得边值问题(15)的左区(-1 和右区(0 (1)前人只针对Legendre 方程边值问题研究了其一维的解式,而本文在前人的基础上研究了复合Legendre 方程的解式.通过研究问题(1),发现其具有相似结构的左、右区解表达式,且该表达式的系数完全只取决于(1)中的左边界条件和交界点的衔接条件. (2)在研究复合Legendre方程边值问题(1)中的左、右相似核函数时,发现其系数完全取决于右边界条件和交界点的条件; (3)通过对相似构造法的研究,我们可以快速找到边值问题的解与边值条件系数之间的关系,帮助我们快速地得到该类问题的解,简化了问题复杂的推导过程,进一步完善了微分方程的求解方法,同时也更加快捷地解决了实际问题.未来,我们将进一步针对更高维的进行研究.
y2=C3Pl2(x)+C4Ql2(x),

C4λQl2(θ)=0,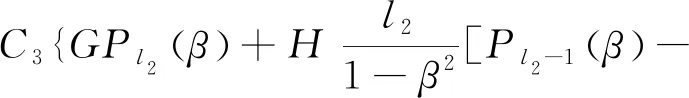
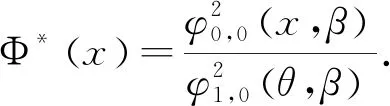


3 相似构造法步骤及应用




4 举例









5 结论和认识
