疫苗生产模型——以2021年五一杯全国大学生数学建模竞赛A题为例

◇四川信息职业技术学院基础教育部 伍 星

2021年五一杯全国大学生数学建模A题要求对10种不同类型的疫苗依次经过四个工位的生产问题进行分析，通过借助excel和python分析附件1中50次模拟生产数据，了解每个工位的生产水平；建立整数规划模型，给出最优生产顺序，采用流水线生产模型，得到生产所需总时间最短；通过建立规划模型安排最高利润的生产计划。

1 背景资料

新冠肺炎肆虐全球，给世界带来了深重的灾难，各国为控制疫情纷纷研发新冠疫苗。由于生产疫苗的规模较大，为安全起见，防止疫苗包装出现混乱，每个工位不能同时生产不同类型的疫苗，疫苗生产不允许插队，即一旦确定进入第一个工位的疫苗生产顺序，就要一直保持不变，而且前一种类型的疫苗离开某个工位后，后一种类型的疫苗才能进入这个工位。

现有YM1-YM10等10种不同类型的疫苗需要生产，每种疫苗生产都需要经过CJ1、CJ2、CJ、CJ4等4个工艺流程。每个工艺流程一次性均能处理100剂疫苗，这100剂疫苗装进一个加工箱一起送进工位的设备进行处理。而且，只有按照CJ1-CJ2-CJ3-CJ4的顺序在4个工位都进行了加工以后，才算完成生产。在此背景下，需要解决如下问题：

（1）疫苗在每个工位上均进行了50次模拟生产，数据参照2021年五一杯数学建模竞赛A题的附件，下面对每箱疫苗在所有工位上的生产时间进行统计分析，为疫苗公司的生产提供参考。

（2）为赶时间，对10种疫苗进行检测，建立数学模型，制定加工疫苗顺序，并计算生产总时间。

（3）要求每个工位每天生产的时间不能超过16小时，且同种类型疫苗生产全部完成之后才能生产另外类型的疫苗。建立数学模型，在可靠性为90%的前提下安排生产方案，计算完成任务的最少时间。

（4）该疫苗生产公司计划在100天内选择部分数量的疫苗进行生产，每个工位每天生产的时间不能超过16小时，每种类型疫苗的生产任务可以适当拆分，以最大销售额为目标，安排生产计划。

2 问题分析

我们需要解决YM1-YM10十种疫苗，经过四个工位CJ1-CJ2-CJ3-Cj4顺序生产，不能改变生产顺序，如何使得耗时最少，效率最高，利润最大，并且在生产时间不固定的情况下，制定生产顺序，使生产更合理化。

对于问题（1），对每箱疫苗在所有工位上的生产时间进行统计分析，为疫苗公司的生产提供参考；这是一个数据分析问题，通过使用Excel和spss等软件处理附件1中的数据，分别从均值、方差、最值、概率分布等统计分析，能够直观了解每个工位生产疫苗的能力水平。我们从三个方面对数据进行加工：首先确定每类疫苗在每个工位上的均值；再确定四个工位生产情况的均值、方差、最值的分析；最后给出每个工位的数据变化的概率统计。

对于问题（2），制定10种疫苗的加工顺序，并计算生产总时间。这是一个线性规划中的二次分配问题，根据题目要求忽略次要的影响因素，让疫苗按一定顺序为主要约束条件，建立相应的加工生产计划总用时最短的整数规划模型。

对于问题（3），此问题可以看成是流水生产过程，重点需要考虑的是生产的均衡性、高效性，使流水线生产率最高，所以建立模型：首先按工序先后顺序，合理地把任务分配给每个工位；其次每个工位的生产时间要尽量接近节拍；最后，各工位空闲时间要小，并且使工位之间负荷均匀，以保证流水线时间损失率最低。

对于问题（4），这是一个线性规划问题，需要找到目标函数和约束条件，利用lingo软件求出最大利润。

3 解决问题

3.1 模型一的建立与求解

针对附件1中给出了每类疫苗在每个工位上进行了50次模拟生产，下面对每箱疫苗在所有工位上的生产时间进行统计分析。首先考虑了每类疫苗在每个工位上的均值，可以看到数据变化比较大，没有规律可循，因此接下来单独从每个工位的生产能力进行分析。

（1）四个工位的生产情况，如表1所示。

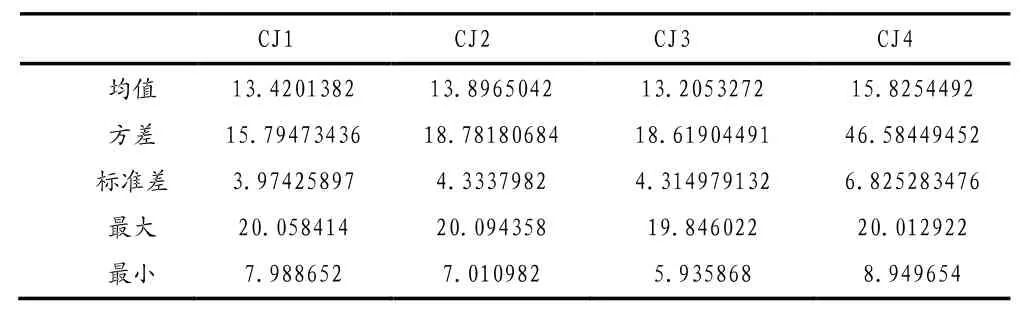
表1 四个工位生产情况

从表1中可以看到，每个工位生产水平差距不大，CJ4相对较弱；从数据的稳定性看，CJ1较好，标准差最小；但四个工位生产的最大最小值差距稍大，可能跟疫苗本身有关。

（2）每个工位的数据变化统计。

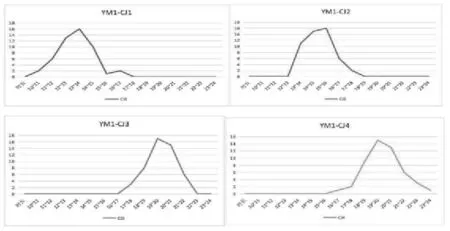
图1 AM1在四个工位分布图

3.2 模型二的模型建立与求解

此问题明显是根据生产顺序的排列组合，求最小生产时间的问题。一共有10种疫苗共有10！种可能的排列顺序。构建一个10×10的0-1矩阵，每行每列仅有一个元素为1，其余元素为0，共有10！种矩阵。我们假设最优的方案已经找到，即第个生产的疫苗为。需要求解最小的加工时间，即第一工位开始工作到最后一工位停止工作的时间最短。转化为最后一个加工的疫苗开始第四道工序的时刻与第四道工序耗时之和即：

又由假设可知每个疫苗依次经过CJ1-CJ2-CJ3-CJ4，所以对于第个加工的疫苗前一个工序的结束时间必须在不晚于下工序完成后才能进行

因此，对这一问题我们构建类整数规划模型，如下：

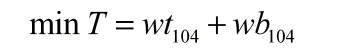
目标函数

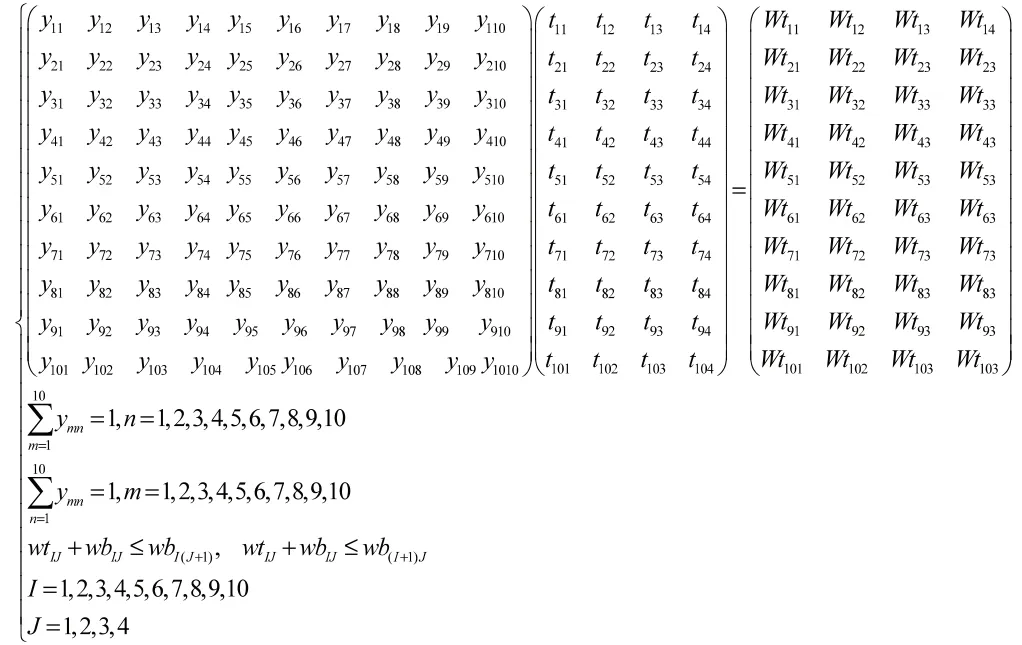
将目标函数以及约束条件转换为编程语言用lingo软件求解结果。最后借助python软件利用10×10的矩阵输入，进行大循环，验证结果的正确性，最终得到加工顺利如下：

YM10--YM9--YM8--YM7--YM6--YM5--YM4--YM3--YM2--YM1

为了更加清晰的说明生产流程，将各个疫苗的开始时间，结束时间绘制时间表，如表2所示。

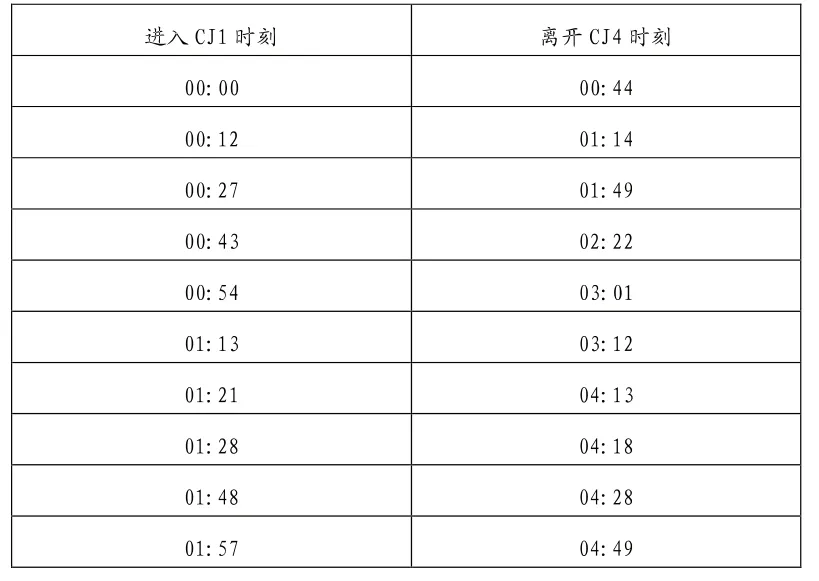
表2 每种疫苗进入和离开工位时间

3.3 模型三的建立与求解

针对附件2中10种疫苗不同规模的生产任务，规定每个工位每天生产的时间不能超过16小时，并且每种类型疫苗的生产任务不可以拆分。因此这是一个流水线生产任务。我们这样建立如下模型：如果第种疫苗在第工位上进行，设，其中。

在可靠性为90%的前提下安排生产方案，为使得使用时间最少，90%确定随机数据中较小的量，取前45组数据的均值，得到每类疫苗在每个工位上所需要的时间，如表3所示。

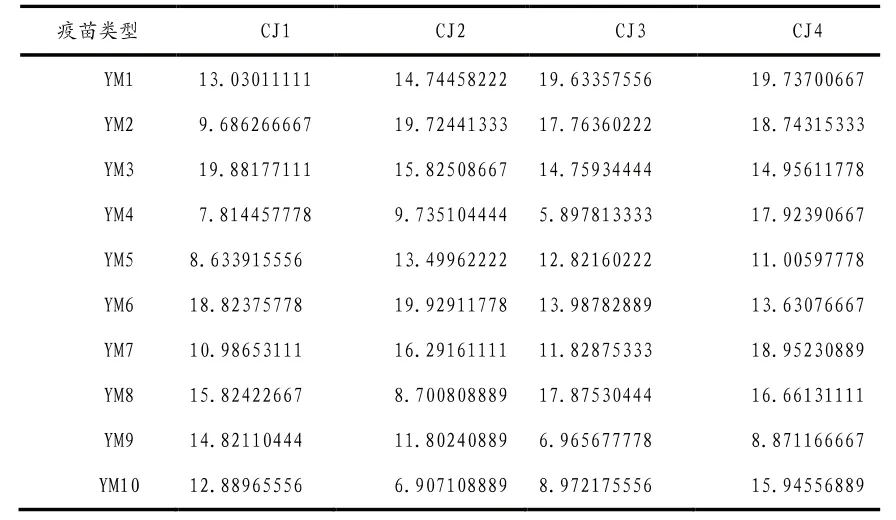
表3 90%较小数据均值

由于同类疫苗在每个工位生产时间相同，又因为每天每个车间最多生产16小时，根据这个约束条件，我们需要找出耗时最多的工位，以此为标准，计算生产每类疫苗每天最大生产量，以及对应生产天数如表4所示。

表4 每天生产量及所需天数

3.4 模型四的建立与求解

疫苗生产公司计划在100天内选择部分数量的疫苗进行生产，每个工位每天生产的时间不能超过16小时，这是一个线性规划问题，需要找到目标函数和约束条件，不妨设每天只生产一种疫苗。设生产每种疫苗的天数为决策变量。即，设生产第类疫苗天，目标函数为：

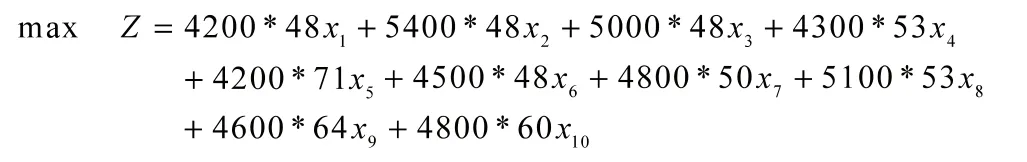
约束条件为：

利用lingo软件计算结果，得到生产每类疫苗的天数如下：

4 结语

解决疫苗生产问题，做了相对理想化的假设。本文选用了线性规划和0-1整数规划模型。对于问题（2）中的模型，当LINGO不能输出所有最优解得情况，在不了解其具解路径时，可以通过改变初始的工件各工序耗时矩阵，求得其它最优解，模型选用简单有效。在考虑数据关系中，利用图表的直观性，清晰明了描述特征。