考虑风电态势的源荷优化调度策略研究

刘海南，樊国旗，刘喆男，田瑛，闫凯文

（1.国网宁夏电力有限公司石嘴山供电公司，宁夏 石嘴山 753000；2.国网金华供电公司，浙江 金华 321017）

0 引 言

规模化下风电并网对国家提出的“双碳”政策起到了巨大作用[1-2]，然而风电的随机波动和不可控特性对电网的经济稳定运行造成不利影响，通过研究风电的特性能让风电并网利益最大化[3-4]。对于风电并网带来的不利因素，文献[5-6]在风电功率进行预测的研究方面应用自回归滑动平均模型，最后得到典型风电出力场景。文献[7-8]通过结合Copula 函数和K-means 算法得到典型的风电场景出力用于无功优化。文献[9]根据风电消纳情况建立3 种源-荷-储优化调度模型，丰富了提高风电消纳水平的手段。考虑到新能源的不确定性，文献[10]通过对新能源、负荷建立概率模型并通过拉丁超立方抽样得到研究场景，求解所建立的优化调度模型验证此方法的有效性。文献[11-13]从系统运行经济性角度出发，对不同类型的需求响应机理进行描述并建立模型，然后构建出优化调度模型。文献[14]通过建立数学模型将典型负荷曲线划分为不同时段，能够更容易得出负荷和风电及光伏功率之间的关系，并通过结果验证其正确性。

上述文献很少考虑在研究风电负荷之间的特性的基础上做出调度策略，因此，提出一种考虑风电负荷态势的优化调度策略：首先，通过K-means 算法和风荷耦合度指标研究负荷高峰、低谷时段的耦合特性；然后，基于此特性提出一种日前日内优化调度策略，通过加入调节常规机组、储能和高载能负荷出力使电网运行利益最大化。

1 风电负荷特性研究

地市级别及更大范围的区域电网的日负荷特性一般为双峰特性，即午间高峰和晚间高峰，有较强规律。典型的日负荷曲线具有双峰性，可以分成负荷高峰时间段、负荷平时间段、负荷低谷时间段去描述风电-负荷之间的联系，典型日负荷各时段风电出力情况如图1所示。

图1 典型日负荷各时段风电出力情况

负荷高峰时间段TH即高于分界线αH·PL,max的部分，其公式表示如下：

式中：PL(t)为t时刻的负荷功率，PL,max为当日最大负荷值，αH为负荷高峰分界系数，一般取0.8±0.1。

负荷低谷时间段TL即低于分界线αL·PL,min的部分，其公式表示如下：

式中：PL,min为当日最小负荷值；αL为负荷低谷分界系数，一般取1.3±0.1。

对于日负荷低谷时间段的电网控制与运行，风电出力影响常规火电机组的深度调峰、机组最小技术出力和电网安全稳定约束下限制风电消纳空间以及电网的调峰裕度；对于日负荷高峰时段的电网控制与运行，风电出力影响电网常规机组的启停情况及机组组合情况、系统调峰和系统旋转备用容量；对于日负荷平衡时段的电网控制与运行，一般情况下各地区的风电装机容量不大于当地负荷总容量，因此在负荷平时段系统处于容易调节的时段。负荷平衡时段下风电量较大，但总量远小于负荷总量，不会造成大量弃风；当负荷平衡时段风电量较小，可以通过常规机组调节来平衡供需两端。

式中：Pw(dt)为d日t时刻风电出力，max(·)为最大值函数。

式中：min(·)为最小值函数。

风电日平均出力Pw,av(dt)的公式如下：

上述指标反应负荷低谷、负荷高峰区间风电和负荷之间的关系：负荷低谷区间风电出力影响电网的弃风量和系统调峰；负荷高峰区间的风电出力影响电网的机组启停计划以及旋转备用量。通过结合上述公式得到风电低谷、负荷高峰时段的耦合系数，公式如下：

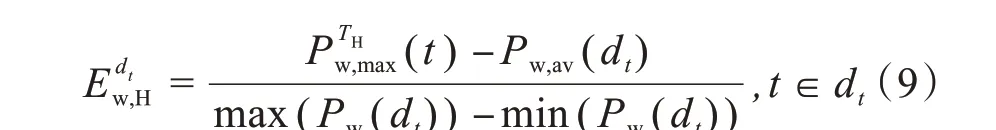
式中：为负荷高峰时间区间的风电负荷耦合系数，表征风电在负荷高峰区间的出力水平和系统调峰需求。如果该值小于零时，即负荷高峰区间的风电最大出力低于当日风电出力的平均水平，负荷高峰区间调峰压力较大。

结合式（8）、式（9）能够得出当日风电负荷时序耦合度指标：

典型风电出力场景一般通过概率的方法或者聚类分析、消除法等得到，本文采用K-means算法来分析风电数据得到典型风电出力场景。以西北某地风电场群的夏、冬季风电出力数据为例，通过K-means 算法得到各季度的典型风电出力曲线如图2、图3 所示。从夏、冬季风电出力场景可见：冬季出力水平较高，夏冬两季典型出力场景都表现出在日间风电出力相对较低，尤其是15：00 左右的区间有着较突出的反调峰特性。对于典型负荷出力场景，负荷变化较小，因此选取夏、冬季节典型负荷出力曲线，如图4所示。

图2 夏季风电出力曲线

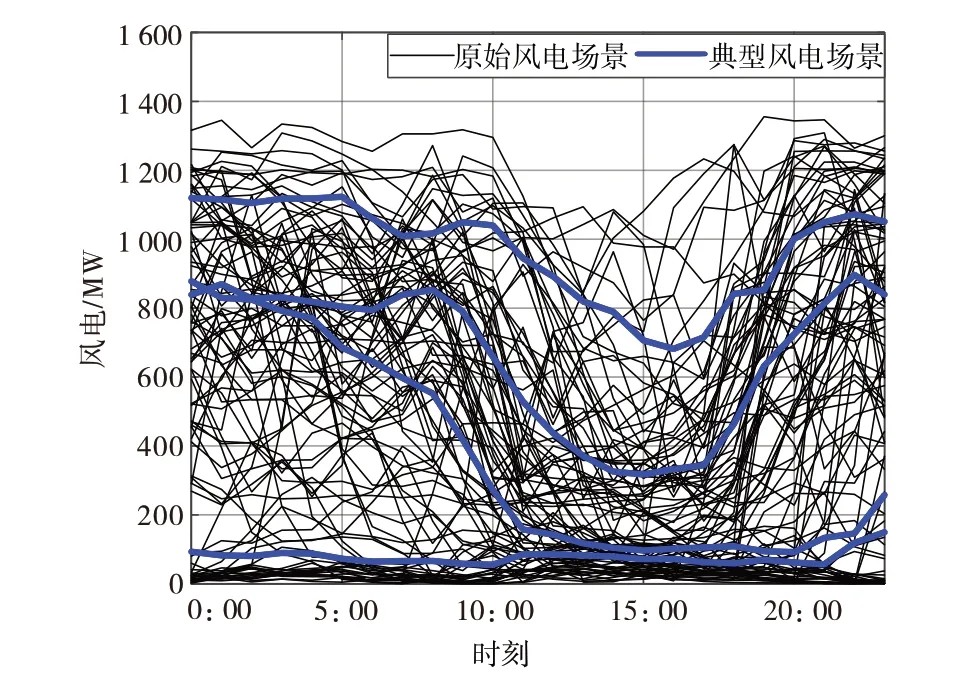
图3 冬季风电出力曲线

图4 典型负荷出力曲线

由于夏季炎热，降温设备的运行使负荷增加，夏季典型负荷出力整体上高于冬季典型负荷出力。最后，以该区域综合风电出力场景和典型负荷出力场景为代表，计算各季节的风电负荷耦合度。日负荷高峰划分系数αH选0.8，日负荷低谷划分系数αL选1.3[14]。通过对典型 冬、夏季负荷曲线的负荷区间划分：夏季典型日负荷谷时段为2：00—5：00，日负荷峰时段为13：00—17：00，其他时段为负荷平时段；冬季典型日负荷谷时段为1：00—4：00，日负荷峰时段为13：00—15：00和17：00—18：00，其他时段为负荷平时段。由于各季节典型风电场景数较多，在各季节风电聚类场景中选取概率最大的作为代表。通过计算得出：夏、冬季的典型日负荷曲线和该季度的典型风电出力曲线的耦合度分别为0.328，0.054。夏、冬季的风电负荷耦合度值都大于0，即负荷低谷时段风电出力大于当日风电平均出力，对系统调峰有一定影响。

2 可调度资源“源-荷”特性分析

2.1 火电机组

常规火电机组指纯凝式火电机组，蒸汽全部进入汽轮发电机的汽轮机，只发电不供热，各级叶片做工，乏汽都凝结成水。常规火电机组的发电效率高，其最小技术出力一般为额定出力的60%，深度调峰可下降至50%，常规火电机组的耗煤量与实际发电相关，本文中关于常规机组耗煤量成本的公式如下：

2.2 高载能负荷

根据某些高载能用户实际生产过程中的调节情况可知，高载能负荷可以分为可连续调节负荷和可离散调节负荷，可连续调节的高载能负荷以电解铝为例，可离散调节的高载能负荷以铁合金为例，电解铝和铁合金的出力公式如下：

3 基于风电-负荷时序耦合特性的优化调度

3.1 日前、日内优化调度模型

首先，基于风电负荷时序耦合分析，在风电负荷耦合时段将可离散调节的高载能负荷纳入调度计划，将风电功率小、负荷功率大的时刻的可转移负荷转移至风电功率大而负荷功率小的时刻，配合常规机组出力，日前调度以系统成本最优目标建立模型并形成日前计划，公式如下：

由于风电和负荷日前预测功率和日内超短期预测功率存在误差，因此日内优化调度策略针对此误差进行修正，通过调节常规机组和可连续调节的高载能负荷达到电力系统供需平衡，日内优化目标以风电消纳量最大为目标：

式中：Ptw为t时刻风电出力，其他约束见参考文献[9]。

3.2 算例情况

算例分析数据取自某地，该地区火电容量1 415 MW，风电装机容量945.5 MW，弃风价格350 元/（MW·h），应用自适应粒子群算法对算例进行求解，电解铝和铁合金的参数见表1。

表1 电解铝和铁合金的参数

3.3 算例仿真

日前优化调度策略以电网最经济运行成本为目标，日前优化后的风电消纳效果见图5、图6。

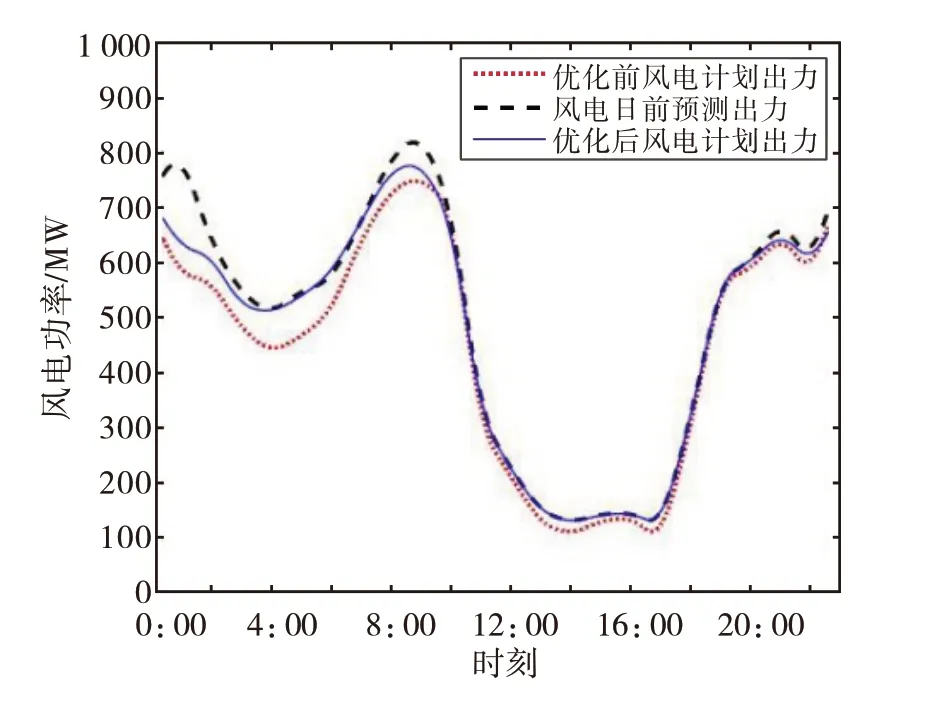
图5 日前优化后风电消纳效果场景一

图6 日前优化后风电消纳效果场景二

由图5、图6可见日前风电预测曲线，场景一的耦合时段为0：00—5：00和18：00—23：00；场景二的耦合时段为7：00—9：00 以及15：00—19：00。由于可离散调节的高载能负荷持续调节时间限制，图7中可见可离散电解铝负荷的调节情况，以及可连续调节负荷铁合金的调节情况，图8 不再赘述。

图7 日前优化后高载能负荷运行场景一

图8 日前优化后高载能负荷运行场景二

采用本文所提优化调度策略后，调度周期内总弃风量为110.9 MW·h,由于高载能负荷可调节量及持续时间等限制，弃风时段多集中在3：00—5：00，而传统调度的弃风量为650.9 MW·h，通过将风电波动分类并将可离散、可连续调节的高载能负荷纳入优化调度计划能够很大程度上提高风电消纳，优化前后系统运行成本如表2所示。

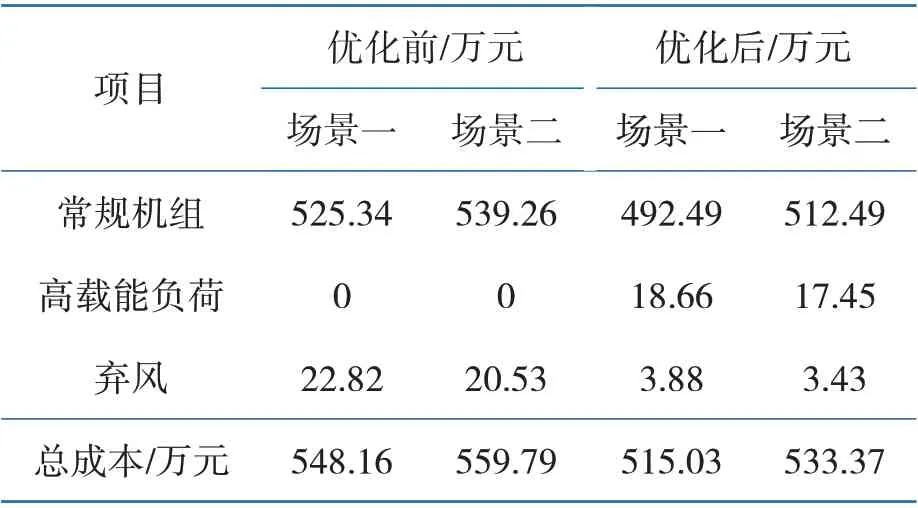
表2 系统运行成本对比

由表2 可知，在采用本文所提优化调度策略后场景一系统总成本减少33.13 万元，场景二节约成本26.42 万元。利用可离散、可连续调节高载能负荷显著减少了弃风成本，系统成本降低的同时也提升风电消纳量。

相对于日前风电预测，日内15 min 风电预测提高了精度，也提高了时间粒度，而可连续调节的铁合金负荷可以追踪风电波动，平抑日前日内之间风电预测值的偏移量，如图9所示。

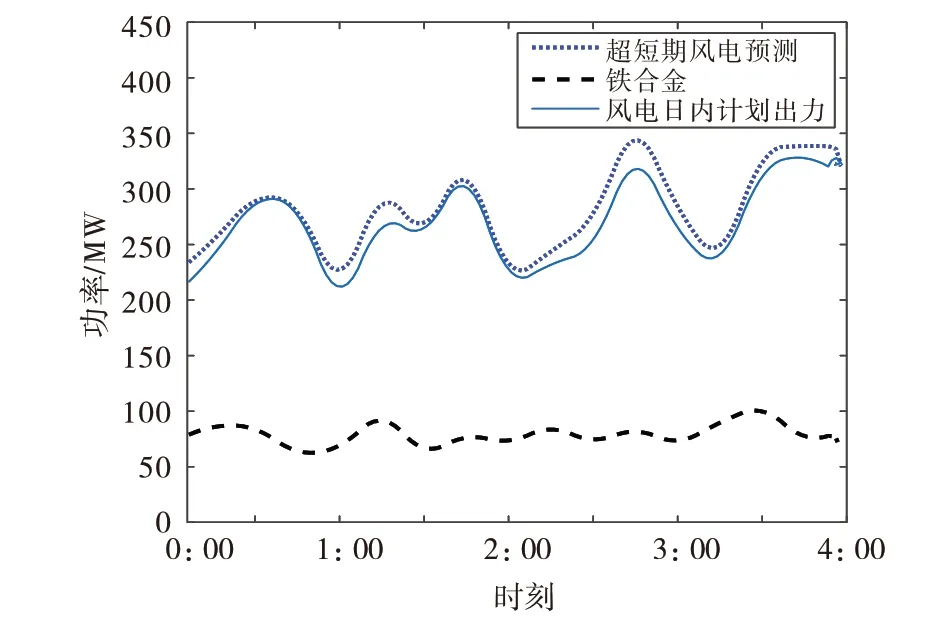
图9 日内风电预测及铁合金出力

在24：00—4：00，可连续调节的铁合金负荷的出力情况能够在其调节范围里最大化追踪风电预测误差带来的波动，在风电波动量较大的夜间时段，其优化调度周期内风电超短期预测总量为1 023.6 MW·h，通过调节常规机组及可连续调节的铁合金负荷应对风电波动，弃风量为84.1 MW·h，弃风量不超过总量的10%，有效提高系统风电消纳量。

4 结语

对风电曲线与负荷曲线之间的关系进行研究并提出方法，应用该方法对西北某地风电场群出力和当地负荷出力进行分析，得出两者之间的耦合关系，在此基础上建立调度优化模型，基于风电态势划分下建立的风电消纳模型，结合高载能负荷特性平抑风电大、中时段波动，不仅在一定程度上节约了系统运行成本而且有效提升风电消纳量，对地市级电力系统调度具有指导价值，此外以西北某地电网进行计算分析验证所提策略的有效性。