基于图卷积网络的运动想象识别

许学添，蔡跃新

1.广东司法警官职业学院 信息管理系，广州510520

2.中山大学孙逸仙纪念医院 耳鼻喉科 听力学与言语研究所，广州510120

脑-机接口（brain-computer interface，BCI）作为大脑神经活动与外部物理世界的连接桥梁，将大脑活动信息转为计算机指令，从而控制外部设备，可以有效地帮助残疾人、老年人等活动能力受限的人。脑电图（electroencephalogram，EEG）由于其低成本和非入侵等优点，在BCI系统中得到最多的应用与研究[1]。基于EEG的运动想象分类与识别是脑机接口的一个重要研究方向，特别是近年来，结合深度学习算法，BCI 系统的发展取得了巨大的进展[2]。

运动想象EEG识别经历了从早期的特征统计到结合机器学习算法进行分类识别[3-5]，再到当前的深度学习阶段，识别效果在不断提高，特别是结合深度学习算法，可以自主学习信号不同层次的特征，避免人工参与的特征工程，因此在识别准确率上取得较大的突破。利用深度学习自主提取样本抽象特征的能力，许多研究将卷积神经网络（convolutional neural networks，CNN）、长短期记忆网络（long short-term memory，LSTM）、深度玻尔兹曼机（deep Boltzmann machine，DBM）等方法应用到运动想象脑电分析中，并取得较好的识别效果。Schirrmeister 等[6]研究了一系列不同结构的卷积神经网络，设计用于解码原始脑电图中想象或执行运动的不同模型；Lu等[7]提出了一种基于受限玻尔兹曼机（restricted Boltzmann machine，RBM）的深度学习算法，通过快速傅里叶变换和小波包分解得到脑电图信号的频域表示，输入三层RBM 与一个额外的输出层叠加，完成分类任务；Wang 等[8]将运动想象EEG 时间序列分割为等长的片段，并计算均值，再通过一组空间滤波器以确定不同节点通道的权重，最后输入LSTM网络进行分类；胡章芳等[9]设计了一个多层卷积双向LSTM 型递归网络，利用多层的卷积神经网络提取EEG 信号的频域特征，再用LSTM网络提取时域特征，最后完成分类；唐智川等[10]将脑电信号事件相关去同步和事件相关同步模式下的EEG 功率值作为分类特征建立矩阵，再用CNN 网络进行学习分类。

目前基于深度学习的脑电信号分析，主要是将EEG信号当作二维矩阵，或者将EEG 信号的特征转为图像（时频图、FRMI 图等），再通过CNN、LSTM 等经典的深度学习算法进行特征提取，这些样本对象均为欧式空间的规则数据，对节点已经进行了默认的排序，在提取抽象、高层的EEG 信号特征时没有考虑大脑不同区域神经元之间的关联信息，也即节点的空间结构信息在研究是中被忽略的。图卷积网络（graph convolution network，GCN）[11-12]是在非欧式空间结构数据上的深度学习，将传统的离散卷积思想应用在图结构上以获取节点特征信息在图结构上不同层次的谱域表示，能够充分考虑节点自身的特征信息及节点之间的关联信息，更详细深入地描述图信息数据。图卷积网络目前已经在交通预测、信息传播、社交关系、生物结构、动作建模等领域得到广泛应用[13-17]。多路导联电极采集的EEG数据，每个电极节点上的EEG 信号代表了所在大脑区域的神经活动信息，可以抽象为一个由点集和边集组成的图，因此图卷积网络也适合分析多节点的EEG信号。将图卷积网络应用到运动想象脑电信号分析中，结合不同节点EEG信号的时频特征和节点间的图谱特征，可以从全脑域空间的关联中去学习、提取有价值的高层特征信息，以提高运动想象的识别准确率。本文的基本思路是通过不同通道的EEG 信号的相关性建立大脑图结构，再将每个电极上的EEG信号时频特征作为每个节点的输入特征，通过GCN网络进行训练，完成不同运动想象动作的识别。

1 基于图卷积网络的运动想象分类模型

1.1 图卷积网络

图卷积网络分为谱域图卷积网络和空域图卷积网络[11-12]，其中谱域图卷积网络是在图论的基础上发展而来，根据图谱理论和卷积定理将数据从空域转到谱域进行卷积处理，具有严格的理论基础。本文采用图谱卷积模型ChebNet[18]来进行EEG图信息识别。

为了对局部输入维度可变，输入排列无序的图结构数据进行卷积操作。Bruna等[19]首次提出了利用拉普拉斯矩阵来完成谱域图卷积。对于N个顶点的无向图G={E,V,W}，其中V是顶点的集合，E是边的集合，W∈ℝN×N是该图的邻接矩阵。该图的度矩阵为D∈ℝN×N,，该图的拉普拉斯矩阵L=D-W，规一化的拉普拉斯矩阵L=In-D-1/2AD-1/2，In为单位矩阵。对L特征分解得到L=UΛUT，其中U=(u1,u2,…,un)∈ℝN×N为L的特征向量矩阵，Λ=diag(λ0,λ1,…,λn)∈ℝN×N为特征值对角矩阵，ui∈ℝN,i=1,2,…,n,为L的特征向量，λi为对应的特征值。在谱域，x1、x2两个信号的图卷积定义为：

因此对于输入信号x，经过卷积核滤波器g∈ℝn的图卷积运算定义为：

如果将g表示为gθ=diag(UTg)，则x的图卷积运算可以简化为：

谱域卷积都是基于式（3）或者改进而来的。ChebNet图卷积网络用切比雪夫（Chebyshev）多项式代替谱域的卷积核，gθ定义为切比雪夫多项式为Ti(x)=2xTi-1(x)-Ti-2(x),T0(x)=1,T1(x)=x，因此ChebNet图卷积运算为：

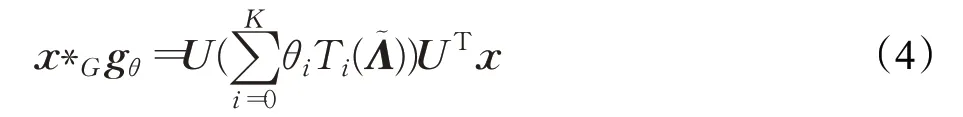
ChebNet 图卷积不需要对拉普拉斯矩阵做特征分解，而且卷积核只有K+1 个可学习的参数，参数的复杂度被大大降低，可以大大提高运算速度。

1.2 系统模型框架

图1 为本文基于图卷积网络的运动想象分类模型。首先根据多路导联节点所采集的EEG 信号建立EEG图信息，包括EEG图结构和EEG信号特征；之后将EEG 信号特征作为图卷积层的输入特征。图卷积层首先经过ChebNet卷积计算，之后经过激活层利用Rule函数进行非线性变化，再经过批标准化（batch normalization，BN）层对可学习参数进行归一化处理，加快训练的收敛速度，最后再经过池化层进行降采样操作，减少运算量，防止过拟合。本项目设置两层图卷积层，提取EEG图信息的高层特征信息，最后再经过一个全连接层和Softmax层输出运动想象分类（左右手、脚、舌头等）。

图1 基于图卷积网络的运动想象分类模型Fig.1 Motion imagery classification model based on graph convolution network

2 运动想象脑电数据及特征提取

2.1 EEG大脑网络

将每个导联电极定义为图中的一个节点，多路EEG信号就能抽象为一个由点集和边集组成的图G=(V,E)，其中V为节点的集合，对应导联节点，E为边的集合，该图的邻接矩阵为W，节点i和节点j的权重ωi,j通过其所采集的EEG 信号的皮尔逊相关系数来表示，计算如下：

其中，EEGi和EEGj分别为第i个节点和第j个节点的EEG信号时间序列，D为方差，COV为协方差。

2.2 EEG脑电特征提取

本文分段获取EEG信号的时频特征作为图卷积网络的节点输入特征，主要分为时域特征和频域特征。时域特征包括EEG信号的标准差、均方根、信息熵三个指标。频域特征主要计算EEG信号在δ、θ、α、β四个频段的能量谱值。时频特征的计算如表1。因此每个节点的输入特征为x=(xrms,xstd,xent,xEδ,xEθ,xEα,xEβ)，所有特征在经标准差标准化之后再输入图卷积网络。

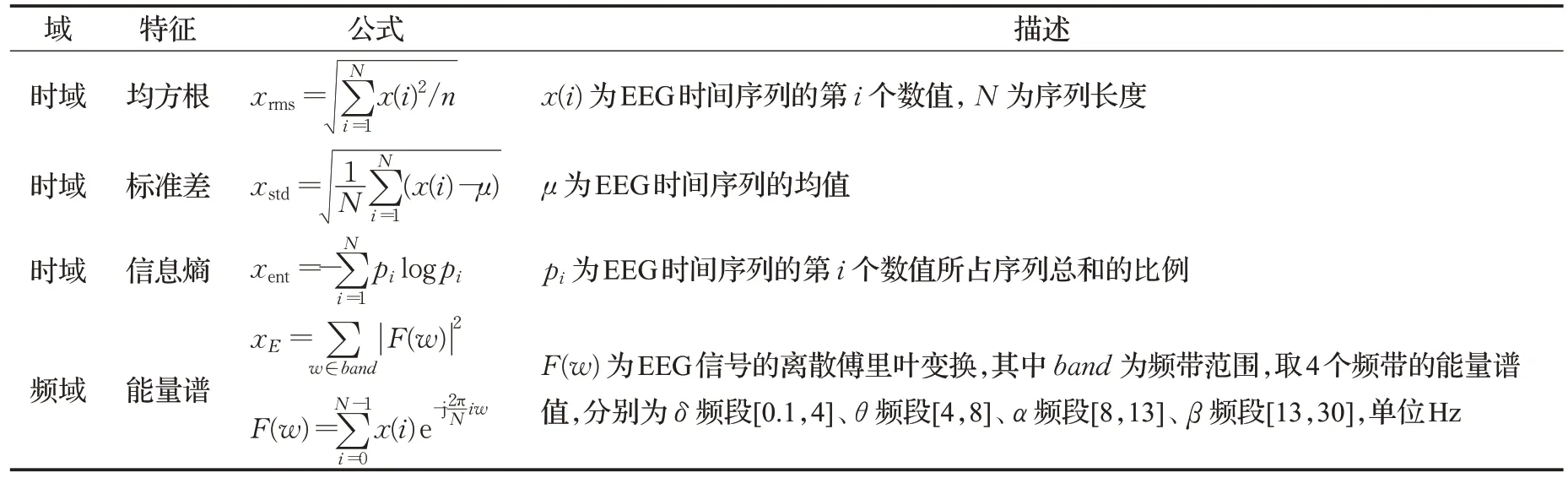
表1 EEG信号时频特征Table 1 Time frequency features of EEG signal

2.3 实验数据介绍

本文的实验数据集采用的是BCI Competition IV Dataset 2a（http：//www.bbci.de/competition/iv/），运动想象的类型有4种，分别为左手、右手、脚和舌头。数据采集电极分布如图2 所示，单极记录所有信号，共有22 个EEG 通道和3 个EOG 通道，以左乳突为参照，右乳突为地信号。信号采样频率为250 Hz，带通滤波范围为0.5～100 Hz，放大器的灵敏度被设置为100 μV，另外一个50 Hz陷波滤波器被用来抑制线噪声。

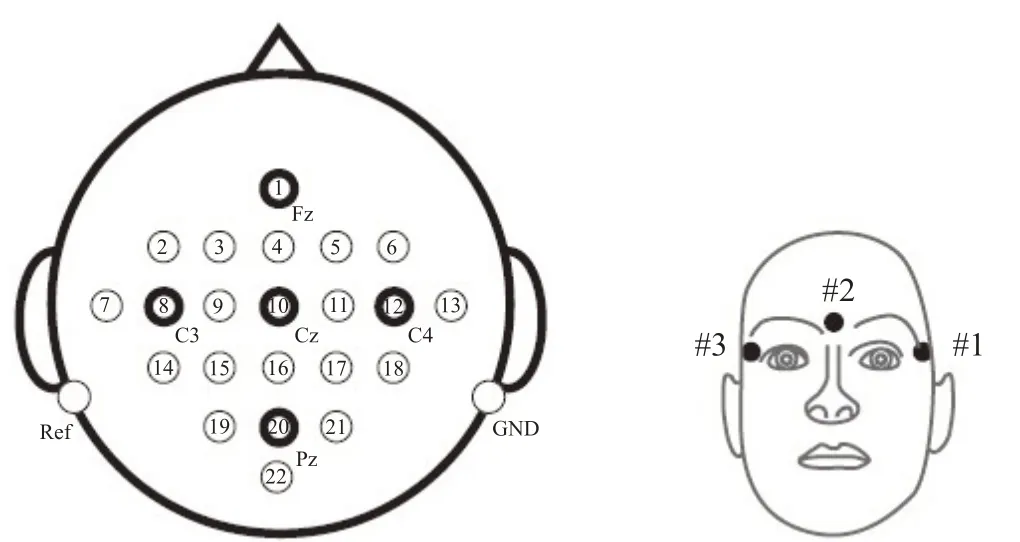
图2 电极示意图Fig.2 Electrode diagram

数据采集范式如图3所示。在每一次实验开始（0 s），会发有蜂鸣声，之后屏幕出现一个固定的“十”字光标，持续2 s，之后出现运动想象标识，持续1.25 s，在第3 s到6 s为运动想象阶段，之后休息，开始下一次实验。数据集总共有9个人，每个人进行6轮的运动想象采集，每一轮4种运动想象类型实验各12次，因此每个人总共有288次的运动想象实验样本作为训练数据集。另外还有相同数量的测试数据集。

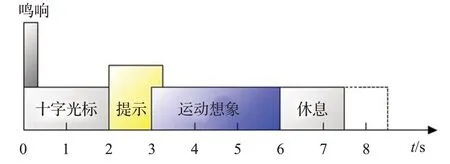
图3 实验EEG数据采集范式Fig.3 Experimental paradigm of EEG data

3 实验及结果分析

3.1 模型参数设置及训练

采用早停法（early stopping）来进行模型训练，以获取最优的泛化性能，防止过拟合。将训练数据集的30%作为验证数据集，训练时只训练剩下的70%数据，训练停止的条件为：（1）以10个epoch为一个训练周期，在一个训练周期后，在验证集上验证测试结果，如果连续5个训练周期验证数据集的最低误差值都没有变化，则停止训练；（2）超过最大训练次数500，则停止训练。模型训练batch 大小设置为60，反向传播训练，使用自适应动量估计优化器（adaptive moment estimation，Adam）进行参数学习，学习速率为0.000 1，采用交叉熵（cross entropy）指标作为损失函数。

停止训练后对测试数据集进行检验，由准确率Accuracy和kappa系数来衡量分类结果。准确率为运动想象正确识别的比例，kappa系数为：

其中，kappa 系数的计算基于混淆矩阵，p0即为分类准确率，pe为预期与实际一致性的概率。kappa系数用来表示分类识别的一致性级别，如表2所示。

表2 kappa系数一致性Table 2 kappa coefficient consistency

3.2 模型参数分析

图卷积层是本文运动想象分类模型的核心，其参数设置决定了分类的准确率。ChebNet 的卷积核具有严格的空间局部性，其中切比雪夫多项式的阶数K就是卷积核的“感受半径”，K值越大，节点就能获取更多其他节点的特征信息进行聚合，但是也会加入更多的无关信息。另外，图卷积层的数量，也会影响模型分类的准确率。不同的切比雪夫多项式的阶数K和图卷积层数对模型的分类性能影响如图4 所示，当K取值为2，图卷积层的层数取2时，可以得到最佳的分类准确率。

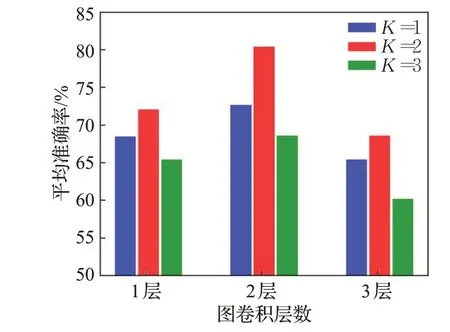
图4 阶数K 和图卷积层数Fig.4 Order K and GCN layers

3.3 实验结果

对于BCI Competition IV Dataset 2a数据集，本文所介绍的图卷积网络模型取得的准确率和kappa系数如表3所示。9名受试者4种运动想象类型的识别准确率达到80.9%，平均kappa系数为0.74，能够取得较好的分类效果。

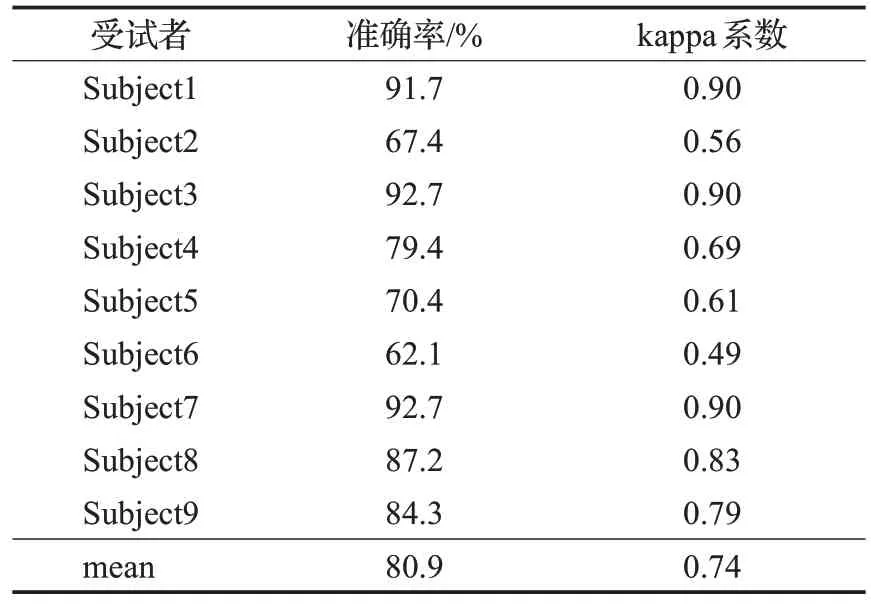
表3 9名受试者实验结果Table 3 Experimental results of 9 subjects

9名受试者在测试数据集上的分类结果混淆矩阵如图5 所示。每个子图为每名受试者的混淆矩阵，横、纵坐标代表预测和实际的运动想象分类类型（LH、LR 为左、右手，F 为脚，T 为舌头），中间数值为对应分类概率。根据kappa 系数，有4 名受试者取得了几乎完全一致的识别效果，有3 名受试者取得高度一致的识别效果，Subject2和6受试者的识别效果相对较差（中等识别效果），主要是由于脑电信号采集时干扰较大、不稳定和样本数量不足。另外，由于图卷积网络属于非结构化数据的深度学习算法，其本质是收集网络中不同节点的特征进行聚合和传递，进而选择节点最优的高层抽象特层，因此如果样本数量不足会导致无法训练学习到最佳的谱域和时频域特征，影响算法的泛化性能。

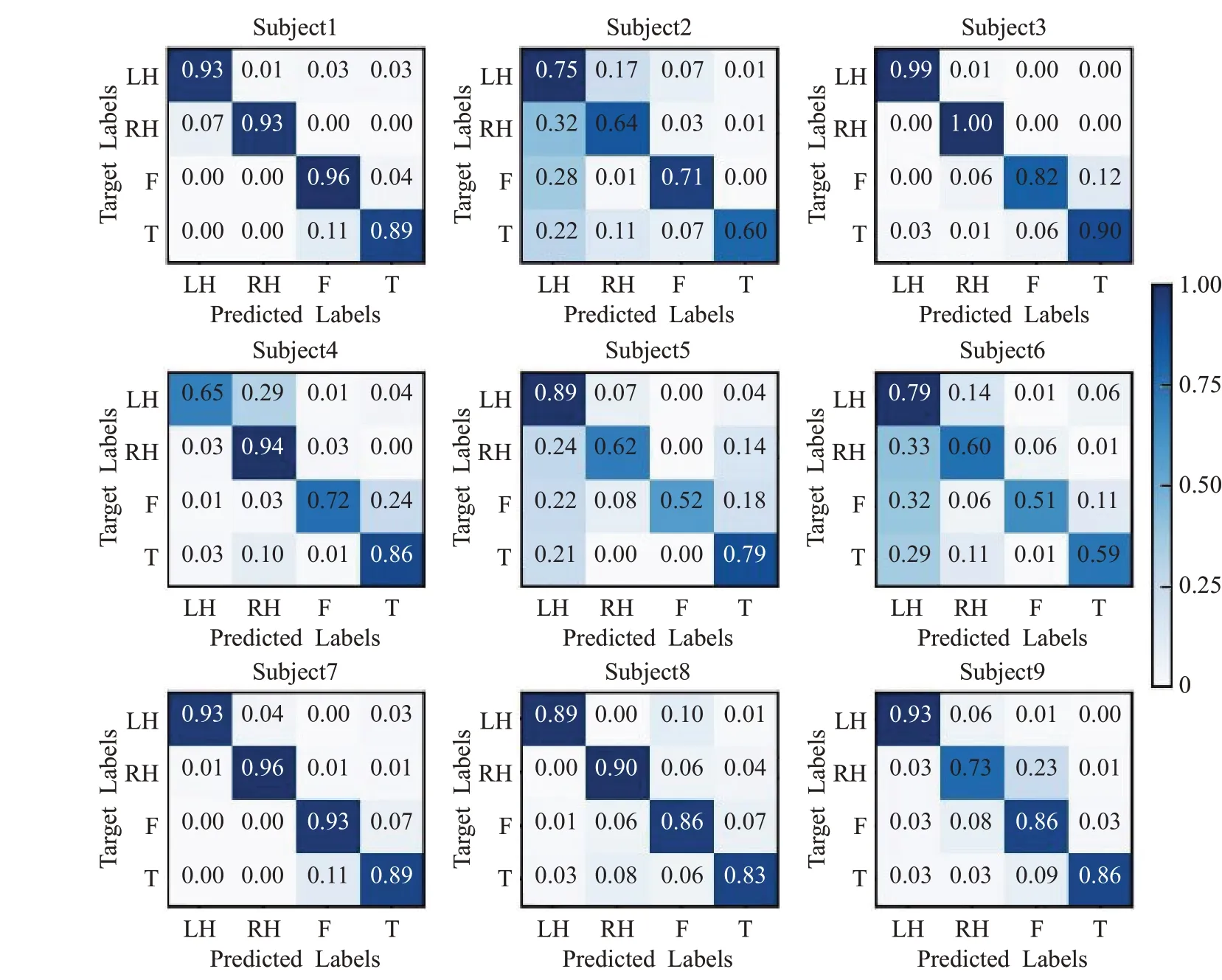
图5 受试者分类结果混淆矩阵Fig.5 Confusion matrix of subject classification results

3.4 方法比较

为了评价验证本文所提出图卷积模型的有效性，与其他文献的方法进行比较，分类的准确率如表4所示。

表4 不同方法比较结果Table 4 Comparison results of different methods

FBCSP[3]属于经典CSP 算法的改进，主要是利用脑电信号矩阵找到一组最优空间滤波器进行投影，再结合机器学习分类算法进行识别；FDBN[7]通过快速傅立叶变换和小波包分解获取EEG 信号的频域数据，再利用三个波尔兹曼机来训练；Shallow ConvNet 和Hybrid ConvNet[6]采用两种类型的CNN网络来处理EEG数据，Shallow ConvNet卷积核长度较长，网络层数较少，Hybrid ConvNet 卷积核长度较短，网络层数多；AX-LSTM[8]采用时间序列的符号化表示EEG 数据，再通过信道加权引入一组空间滤波器作为隐藏层，将其输出反馈给LSTM 网络以完成分类识别。本文则是将EEG 脑电图转化为图结构信息，再利用图卷积神经网络来学习图谱域和时频域信息，完成运动想象分类，在四分类问题上可以取得较好的分类效果。

4 结束语

本文提出了一种基于图卷积网络的EEG信号运动想象识别方法，根据多路导联节点采集的EEG 信号建立节点的关联图结构，并提取每个节点上EEG 信号的时频特征作为输入特征进行谱域图卷积运算，获取大脑图信息的高层、抽象特征，最后通过全连接层输出想象分类结果。在BCI Competition IV Dataset 2a 数据集上取得80.9%的准确率和0.74的kappa系数。本文方法在提取EEG 信号特征时既考虑信号的时频特征，又结合节点网络的谱域空间信息，因此能取得较好的分类效果，为多路EEG 信号的运动想象分类识别提供一种新的思路。