布朗运动研究方法错误及纠正

高 宏

（清华大学，北京 100084）

0 引言

布朗运动不仅是物理学中的一个著名物理现象，也是随机过程理论中的一个基本随机过程。1827年，英国植物学家布朗（Robert Brown）用显微镜观察悬浮在液体中的花粉微粒时，发现在无外界作用的情况下，花粉微粒总是在做无规则运动。后来人们发现，这是一种广泛存在于自然界、工程技术和人类社会等领域中的随机运动现象，如空气中的污染扩散、电子器件中的热噪声和股票市场中的价格波动等，因此这类动态随机现象被称为“布朗运动”。1905年，爱因斯坦认为布朗粒子的不规则运动是由于受到大量液体分子的高速碰撞而引起的，并首次使用概率分析方法推导出了布朗粒子在t时刻位移x(t)的概率密度分布函数f(x,t)，得出了“布朗粒子位移服从正态分布”“布朗粒子平均位移与时间的平方根成正比”和“布朗粒子瞬时速度无穷大”等著名论断。爱因斯坦对布朗运动的定量研究不仅扩大了经典力学的概念和应用范围，而且也开启了其它学科借助概率分析方法研究随机现象的大门，为随机过程基础理论的建立和发展开辟了道路[1]。

随着现代物理学实验手段的不断进步，人们发现布朗运动理论出现了一系列与经验事实不符的反常问题。例如美国德克萨斯大学的李统藏在2010年首次通过激光光镊实验方法观测到了单个布朗粒子的瞬时速度波形[2]，直接颠覆了爱因斯坦“布朗粒子瞬时速度无穷大”和维纳“布朗运动路径处处不可导”的著名论断，导致布朗运动理论陷入严重的范式危机。

本文从随机过程的定义及概念出发，分析了爱因斯坦在研究单个布朗粒子在t时刻的位移x(t)时，用概率密度分布函数f(x,t)来描述布朗粒子位移x(t)的研究方法错误。概率分析方法无形中将x(t)的定义域从时域T改变为样本空间Ω，导致数学研究对象从样本函数变为随机变量，只能用刻画大量布朗粒子集体行为的统计规律用来描述单个布朗粒子的个体行为，从而得出了一系列与事实不符的错误结论。本文将布朗粒子在t时刻的位移x(t)还原为时间函数，根据爱因斯坦的“布朗粒子在不同时间间隔中的运动相互独立”假设和李统藏的布朗运动瞬时速度测量结果，提出了“布朗粒子瞬时速度等于白噪声”的布朗运动定律，建立了可正确描述布朗运动现象、特征及规律的质点运动学方程。

1 布朗运动理论出现的反常问题

科学理论的内容必须要正确反映事物的运动规律，从科学理论推出的可检验结论应该与实验检验的结果相符。反常问题通常是指已有科学理论出现了与经验事实不符，或与其他科学理论发生矛盾的现象。反常问题是科学研究的逻辑起点，常常引导人们进入研究并做出重大发现，从而导致新的概念、方法和理论推翻并替代原有教科书的内容，把人类对客观世界的认识提高到一个崭新的水平。

1.1 位移公式与牛顿力学不一致

牛顿运动定律是质点做机械运动时遵从的基本定律。朗之万依据牛顿第二定律，建立了布朗粒子沿x轴方向进行一维运动时的动力学方程[3]

式中，m为布朗粒子的质量；f(t)为布朗粒子在液体中运动受到的黏滞阻力，f(t)与布朗粒子的运动速度成正比；F(t)为液体分子对布朗粒子高频碰撞产生的平均作用力。

朗之万利用式（1）对大量的布朗粒子求平均，计算出了大量布朗粒子在t时刻的均方位移

式中，D为扩散系数。

爱因斯坦早在1905年就利用概率分析方法推导出了式（2）的均方位移关系式，并借助这个方程来计算一个布朗粒子在x轴方向上平均经历的位移，给出了著名的布朗粒子位移公式[4]

表明布朗粒子的位移与时间的平方根成正比，与牛顿力学质点位移与时间成正比的结论不一致，布朗运动理论与牛顿力学在逻辑上不能自洽。

1.2 瞬时速度与物理学实验结果不符

根据式（3）的爱因斯坦位移公式，布朗粒子在时间Δt内的位移Δx与Δt的平方根成正比，因此布朗粒子在t时刻的瞬时速度为

即布朗粒子的瞬时速度无穷大。

爱因斯坦论证说，耗散力在如此短的时间尺度内改变了一个悬浮粒子速度的方向和大小，以至于使它无法测量[1]。维纳基于式（3）的爱因斯坦位移公式，从数学上证明了“布朗运动样本轨道处处不可导”的著名论断。

2010年，美国得克萨斯大学的李统藏成功地利用激光光镊技术首次实验测量到了悬浮布朗粒子的瞬时速度[2]，完成了爱因斯坦在100多年前认为不可能完成的任务。李统藏的实验结果表明，布朗粒子的瞬时速度是RMS（Root Mean Square）均方根为0.422 mm/s的零均值白噪声，表明布朗运动的瞬时速度（导数）不仅存在，而且可观测。

李统藏的实验结果颠覆了现有布朗运动理论“布朗粒子瞬时速度无穷大”和“布朗运动样本轨道处处不可导”的结论，布朗运动理论因无法解释李统藏的实验事实而陷入严重的危机。

1.3 正态分布性质与事实不符

爱因斯坦在1905年发表的《关于热的分子运动论所要求的静止液体中悬浮小粒子的运动》论文中，首次用概率分析方法对布朗运动进行了定量研究。

爱因斯坦首先假设，布朗粒子在各个不同的时间间隔中的运动，必须被看作是相互独立的过程，并用概率分布来描述布朗粒子在时间间隔Δt上的位移Δx，通过扩散方程推导出了布朗粒子在t时刻的概率密度分布函数：

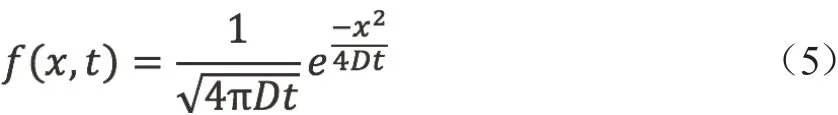
式中，D为扩散系数。

显然，布朗粒子在t时刻的位移x(t)服从参数为（0，2Dt）的正态分布。

从随机过程的角度看，爱因斯坦的假设和概率分析方法，实际上是将不同时间间隔Δt上的位移Δx假设为独立同分布随机变量，根据“独立同分布随机变量之和服从正态分布”的中心极限定理，可直接得出布朗粒子服从正态分布的结论。

如果布朗粒子在t时刻的位移x(t)服从（0，σ2t）正态分布，那么根据正态分布的性质，布朗粒子位移曲线x(t)应具有如下两个正态分布特性：

（1）对称性。在任意时刻，绝对值相等的正、负位移出现的次数大致相等。

（2）集中性。在任意时刻，布朗粒子在0点附近出现的次数最多。

质点在t时刻的位移x(t)是时间t的连续函数，根据正态分布的对称性和集中性，可画出服从（0，σ2t）正态分布的质点位移x(t)的仿真曲线（图1）。

图1 服从正态分布的质点位移曲线

图2给出了1 000个从原点出发的布朗粒子位移曲线。几乎每条曲线都随时间不断远离原点，完全不满足正态分布的对称性和集中性，因此布朗粒子位移曲线不服从正态分布。

图2 布朗粒子位移曲线（1 000个）

事实上，这1 000个布朗粒子在t时刻的空间位置服从（0，σ2t）正态分布，而式（5）的概率密度函数f(x,t)描述的就是大量布朗粒子在t时刻空间位置分布规律，而非一个布朗粒子位移x(t)在t时刻的概率分布。

爱因斯坦和朗之万的研究对象虽然是单个布朗粒子在t时刻的位移x(t)，但由于使用概率分析方法，无形中导致数学研究对象从样本函数改变为随机变量，因而得出的概率密度函数f(x,t)是描述大量布朗粒子集体行为的统计特性。

若将刻画大量布朗粒子集体行为的统计规律用来描述单个布朗粒子的个体行为，就如同用温度来度量一个分子的动能一样，势必会出现一系列与事实完全不符的反常问题。

如果科学理论出现了一系列与经验事实不符的反常问题，表明科学理论已进入“范式危机”阶段，科学知识体系将发生根本性的变革，从而使人类对客观世界的认识发生质的飞跃，并对人类社会实践产生巨大影响。

2 布朗运动研究方法错误分析

数学上的随机过程是从客观世界动态随机现象中抽象出的一种数学结构，是人脑对动态随机现象数量关系及空间形式的思维反映，可以用来描述并揭示布朗运动的数量关系、空间分布及其变化规律。

随机过程基本概念虽然远离了直观的经验世界，但却能更深刻地反映动态随机现象的本质。随机过程的定义涉及随机过程、随机变量和样本函数三个基本概念，在应用时很容易混淆随机变量和样本函数的内涵与外延，导致物理研究对象错位，得出与事实不符的结论。

图3为随机过程定义示意图，假设在随机试验中观察3个质点的不规则运动，可得到左边所示的3条位移曲线，这3次测量结果可分别用3个时间函数x1(t)，x2(t)，x3(t)表示。

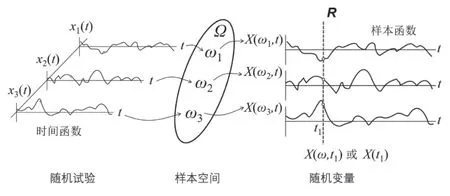
图3 随机过程定义示意图

由于随机试验的结果是一族时间函数，因此我们可用定义在Ω×T上的二元函数X(ω,t)来描述随机试验的所有结果，下面给出二元函数X(ω,t)在四种不同情况下的含义：

（1）固定ω，X(ω,t)是一个自变量为t，定义域为T的普通函数，它是一次随机试验所得到的一条记录曲线或一个时间函数x(t)，通常称为随机过程的一个样本函数（轨道）或一个物理实现。样本函数x(t)从时间维度刻画了单个质点的不规则运动过程。

（2）固定t，X(ω,t)是一个定义在样本空间Ω上的单值实数函数，也就是概率论中的随机变量，简记为X(t)。随机变量X(t)从空间维度描述了所有质点的集合在t时刻的位置分布。

（3）固定ω，固定t，X(ω,t)是一个实数，表示某次随机试验在t时刻的观测值。

（4）当ω和t均变化时，随机试验的所有可能结果构成一族样本函数，所有这些样本函数的总体或集合就构成了随机过程。

综上所述，我们可以给出两种等价的随机过程定义。

定义1：随机过程是一族依赖于样本空间的样本函数集合。

定义2：随机过程是一族依赖于时间的随机变量集合。

在概率论中，样本空间中的样本点被映射成实数轴上的一个点；而随机过程则是将样本空间中的样本点映射成一个时间函数（随时间变化的实数）。定义1把随机过程看成一组样本函数的集合，这是概率论随机变量定义的推广，而定义2把随机过程看成一族有时间标记的随机变量集合。

在工程技术领域，观测到的实验结果就是样本函数的集合，因此常用定义1描述实际随机现象。定义2与概率论中的多维随机变量理论相联系，因此数学领域在研究动态随机现象时常用定义2，可直接使用多维随机变量理论来分析随机过程的统计规律。

样本函数x(t)是时间t的一般函数，而随机变量X(t)并不表示X(t)是时间t的函数，X(t)是样本点ω的函数，X(t)只表示所有样本函数在t时刻的取值，即X(t)={x1(t)，x2(t)，x3(t)}。

随机变量X(t)和样本函数x(t)是两个具有完全不同定义域和值域的函数（表1）。在实际应用中，随机变量X(t)和样本函数x(t)描述的是完全不同的物理对象。样本函数x(t)用来记录或描述一个布朗粒子的位移随时间变化过程，随机变量X(t)则用来描述大量布朗粒子在某一时刻的空间位置分布状态。

表1 随机变量和样本函数的研究方法

概率密度函数f(x,t)是描述随机变量X(t)各种取值可能性大小的数量指标，对于布朗运动，概率密度函数f(x,t)描述的是大量布朗粒子在某一时刻的空间位置分布规律。

由于随机变量及概率概念的抽象性及复杂性，爱因斯坦在研究单个布朗粒子的运动规律时，使用概率分布函数f(x,t)来描述单个布朗粒子在t时刻的位移x(t)[4],[5]，无形中导致数学和物理研究对象均发生错位，只能用刻画大量布朗粒子集体行为的统计规律来描述单个布朗粒子的个体行为，势必会得出“布朗粒子位移服从正态分布”“布朗粒子位移与时间的平方根成正比”和“布朗粒子瞬时速度无穷大”等一系列与事实不符的错误结论。

3 布朗运动瞬时速度

3.1 白噪声

定义：若平稳随机过程样本函数n(t)的均值为零，方差为σ2，如果其自相关函数

式中，τ为时间间隔；δ(τ)为单位冲击函数；则称n(t)为白噪声。

根据维纳-辛钦定理，任意一个均值为常数的广义平稳随机过程的功率谱密度是其自相关函数的傅里叶变换，可得白噪声n(t)的功率谱密度

即n(t)的功率谱密度在整个频率轴上均匀分布，σ2的物理意义代表白噪声信号n(t)在单位电阻上产生的平均功率。

式（6）表明，白噪声n(t)在任何两个不同时刻的取值互不相关。因此，n(t)的信号波形为一串宽度无限窄、方向和大小变化极快的随机脉冲。

3.2 布朗运动瞬时速度

设x(t)为布朗粒子（质点）在t时刻的位移，v(t)为布朗粒子在t时刻的瞬时速度，从信号分析学科的角度看，可将爱因斯坦“布朗粒子在不同时间间隔中的运动相互独立”的假设表述为v(t)在不同时刻互不相关，因此v(t)的自相关函数可表示为

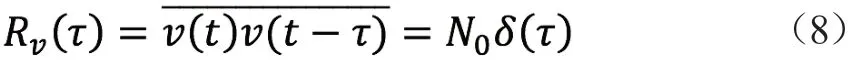
式中，τ为时间间隔；N0为正实常数；δ(τ)为单位冲击函数。

与式（6）对比，布朗运动瞬时速度v(t)显然为平均功率为N0的白噪声，与美国得克萨斯大学李统藏的布朗粒子瞬时速度测量实验结果完全相符。

4 布朗运动定律

根据爱因斯坦“布朗粒子在不同时间间隔中的运动相互独立”假设，以及李统藏的布朗粒子瞬时速度测量实验结果，提出“布朗运动瞬时速度为白噪声”的布朗运动定律，用数学公式表示为

式中，n(t)为式（6）定义的白噪声样本函数。

式（9）描述的布朗运动定律，是根据物理学已有的知识、经验及事实，对过去、现在及未来的布朗运动现象及规律所做出的一种假定性和推测性论断，是建立布朗运动理论或推导其他命题的起点和基础。从式（9）经严格逻辑推理得到的相关命题和结论，对布朗运动具有解释和预见功能，能够预测布朗运动的发展趋势和变化结果。

5 布朗运动位移公式

设x(0)=0，根据式（9）的微分方程，可得布朗粒子在t时刻的位移：

式中，n(t)为式（6）定义的白噪声样本函数。

由式（10）可计算出布朗粒子在区间[0，t]上的平均速度

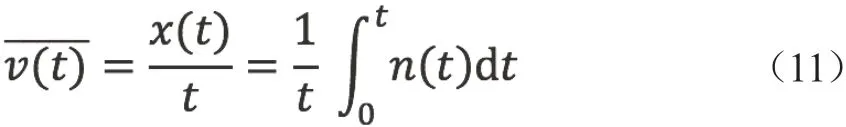
由式（10）和式（11）可得布朗运动位移公式：

即布朗粒子在t时刻的位移x(t)等于其平均速度与时间t的乘积，与牛顿力学质点位移与时间成正比的结论完全一致。

从式（12）可以看出，布朗粒子位移x(t)的运动规律完全取决于其平均速度的特性。由概率论大数定律可知，当t充分大时，平均速度或白噪声n(t)的算数平均值会收敛于一个常数，布朗运动就成为牛顿力学中所描述的匀速直线运动，x(t)趋于一条从原点发出的射线。表明在微观尺度上呈现出随机性的布朗运动，在宏观尺度上具有确定性。

由式（10）的单个布朗粒子运动学方程，也可推导出大量布朗粒子在t时刻的空间位置服从（0，σ2t）正态分布的结论[6]。

6 无规行走实验结果

布朗运动可看作是无规行走（Random Walk）的极限过程。在通常情况下，人们就是利用无规行走数学模型对布朗运动进行计算机仿真实验的。

早在1873年，英国生物统计学家高尔顿（Galton）就专门设计了一个演示无规行走运动规律的实验装置（图4），俗称高尔顿板。

图4 无规行走实验结果

高尔顿板上的钉子呈等边三角形排列，上一层每一颗钉子的位置恰好位于下一层两颗钉子的正中间。当小球从最上面的入口处落下时，碰到第一层的钉子后，随机地向左或向右落下。小球每次落下都会碰到下一层的钉子，然后再次随机地向左或向右落下，直到最后落入高尔顿板底部的一个格子内。

显然，一个小球从入口处经过n层钉子后落入高尔顿板底部格子的过程，就相当于一个小球的n步无规行走过程。小球所在格子偏离高尔顿板中心的距离，就是小球经过n步无规行走后相对原点的位移。

把大量小球逐个从入口处放下，只要高尔顿板的面积足够大、钉子层数足够多，最终落在底部格子内的小球将形成中间高、两边低的钟形曲线，表明大量无规行走的小球在某一时刻的空间位置服从正态分布。

从图2和图4的实验结果可以看出，布朗粒子和小球随时间不断向远离原点的方向扩散，其运动轨迹具有确定性的运动趋势，不具有正态分布的对称性和集中性。

7 结束语

现有布朗运动理论使用概率分析方法研究单个布朗粒子的运动规律，用概率分布函数f(x,t)来描述单个布朗粒子在t时刻的位移x(t)，无形中改变了x(t)的定义域和值域，导致研究对象从单个布朗粒子变为大量布朗粒子的集合，因而只能用刻画大量布朗粒子集体行为的统计规律来描述单个布朗粒子的个体行为，出现了“布朗粒子位移服从正态分布”“布朗粒子位移与时间的平方根成正比”和“布朗粒子瞬时速度无穷大”等一系列与事实不符的反常现象。现有布朗运动理论为自然科学、工程技术和社会科学研究动态随机现象提供了错误的方法和理论，布朗运动理论将面临重大范式变革，基于样本函数的布朗运动理论将替代现有教科书中基于随机变量的错误内容，使人类对布朗运动现象、特征及规律的认识产生质的飞跃，并带动自然科学、工程技术和社会科学的思维方式变革，提高人类认识世界和改造世界的能力，对科学、社会和经济发展产生重大影响。■