一种基于反向学习和伯恩斯坦算子的差分进化算法

熊聪聪，杨晓艺，王 丹，李俊伟，管祥烁

(天津科技大学人工智能学院，天津300457)

差分进化(differential evolution，DE)算法[1]是一种模仿生物群体进化的全局优化算法．与其他进化算法相同，DE算法也是在一个随机生成的初始种群中开始搜索，通过变异、交叉、选择操作产生下一代的种群，不断迭代求解，直至找到最终解．因其具有模型简单、收敛性能好、鲁棒性强等特点，被应用到模式识别、数据挖掘、人工智能等各个领域[2-3]．DE算法与其他群体智能算法相比具有很多优点，但随着研究者的不断深入探索，发现差分进化算法在参数设置中存在着计算开销大、收敛过程中存在着易陷入局部最优和收敛精度不高的缺陷．

针对上述问题，很多研究者对算法进行改进，不断提高算法的收敛速度和精度．比如，为了避免结构参数的试错过程中计算消耗大，Wang等[4-5]提出的算法可以使每个个体在参数池中随机选择参数作为结构参数，而基于正交算子的差分进化(orthogonal crossover differential evolution，OXDE)算法使用正交交叉概率作为结构参数．但这些结构参数的选择方式都是人为设置的，由于缺乏经验而导致的稳定性不足还是无法避免的．于是，研究人员提出了基于自适应的参数调节方式和随机设置参数的方法，如Zhang等[6]提出了基于学习的变异和交叉概率的调整方法，在学习进化过程中成功找到缩放因子和交叉概率等参数信息；Civicioglu等[7]提出了一种非递归并且无参数的差分进化(Bernstain-search different evolution，BSD)算法，这种方法没有设置控制参数的过程，使算法更加简单、高效．

但是，上述算法只是对结构参数的改进，对算法性能的提升有限．为了解决差分进化算法在进化过程中陷入局部最优导致收敛速度过慢的问题，Zhu等[8]提出了一种混合交叉算法，该多目标进化算法通过差分变异策略构造出自适应混合交叉算子，使多目标进化算法的全局与局部的搜索能力得到均衡；童旅杨等[9]通过使用多个差分变异算子增加种群的多样性，从而避免了差分进化算法在进化过程中易于陷入局部最优的问题；Zhang等[10]提出了一种具有排序选择的差分进化(differential evolution with a rank-up selection，RUSDE)算法；钱峥远等[11]提出了一种精英化岛屿的种群差分进化算法，实现了全局搜索和局部搜索能力并重，使算法具有较强的搜索能力与稳定性.

虽然上述文献中提出的改进算法在进化时相对于传统DE算法的性能有了一定的提升，但对算法的改进比较单一，存在着对算法性能提升不足的问题．基于此，本文提出了一种结合参数改进与进化策略改进的算法，即基于反向学习和伯恩斯坦算子的差分进化算法(differential evolution algorithm based on opposition-based learning and Bernstain operator，BODE)．通过对国际标准测试函数进行测试实验，将BODE与已有的优化算法进行了性能比较，结果表明本算法在搜索速度以及搜索最优值的精度上更具有优势．

1 预备知识

1.1 伯恩斯坦多项式

伯恩斯坦多项式(Bernstain polynomial)[12]是逼近连续函数的一系列多项式，它们可以自然地组合成近似于[0，1]上的任何连续函数．二阶伯恩斯坦多项式定义为

其中：n为迭代次数；t为成功的概率，取值范围为[0，1]；s为迭代 n次后实验成功的概率；．通过这个式子可以将固定概率和可变成功次数转移到固定成功次数和可变概率中．通过式(2)可生成(n＋1)大小的n次伯恩斯坦多项式．其中s＜0并且s＞n，Bs,n＝0．

图1为0≤t≤1时二阶伯恩斯坦多项式曲线图．

图1 0≤t≤1时二阶伯恩斯坦多项式曲线图Fig. 1 2nd degree Bernstain polynomials when 0≤t≤1

1.2 反向学习策略

反向学习(opposition-based learning，OBL)策略[13]是反向解与当前解相比较，有高出近50%的概率更靠近全局最优值．反向学习策略的主要思想是对问题进行求解x时，初始值x是通过经验积累或者是单纯的随机猜想，可以同时使用x的相反值尝试得到更好的解x*，使得下一代x能够更快逼近最优解．在种群的进化过程中，如果该个体对应的反向个体的适应值优于该个体的适应值，则反向个体替代该个体，并进入下一代种群．反向学习策略有助于更快地找到最优解，并加快优化算法的收敛速度．

定义1 普通反向学习(generalized oppositionbased learning，GOBL)．假设当前个体 xi(t)在其反向个体第j维上，可定义为

定义2 改进的反向学习(improved oppositionbased learning，IOBL)[14]．假设当前个体 xi(t)=(xi1,xi2,…,xiD)是当前种群中的第i个个体，则对应的反向个体可定义为

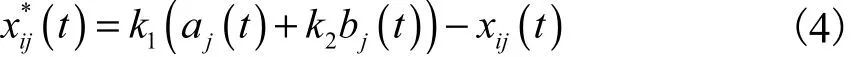
其中：xij属于和k2为(0,1)之间的随机数；表示个体xij在第j维的区间，具体表示为

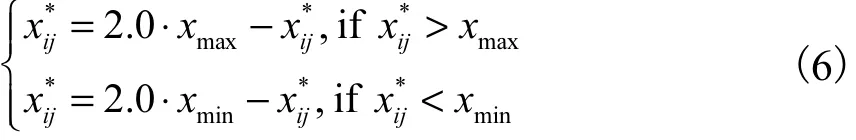
本文对算法改进所选择的反向学习策略为普通反向学习策略．

1.3 差分进化算法

差分进化算法是一种基于种群和定向搜索的优化算法，采用浮点矢量编码生成种群，主要步骤为初始化、变异、交叉和选择．通过个体间的差异获得变异个体，将变异个体按照确定的交叉策略与初始个体进行基因互换后得到交叉个体，选择适应值更好的个体作为新一代种群中的个体，从而在种群的进化过程中随机搜索，直至找到最优值．DE有几种最基本的形式，本文所用的是DE算法中使用最为广泛的一种“DE/rand/1/bin”．

初始化：在D维空间中，假设种群P由N个个体组成，初始的种群在中产生，即

其中：Uj为搜索空间的最大值，Lj为搜索空间的最小值，r and(0,1)是在(0,1)之间产生的一个服从均匀分布的随机数．

变异：对当前种群中的每个个体 Pi(G)产生与之对应的变异个体Vi(G)．F是缩放因子，决定了种群个体差分的步长．F值较大会增强算法的全局搜索能力，但会降低算法的收敛速度；F值较小会导致个体间差异较小，从而使得算法易于陷入局部最优．变异操作可表示为

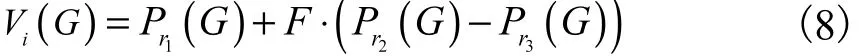
其中：G为迭代次数，r1、r2和r3为集合{1 ,2,…,N } 中任意两两之间互不相等的随机数．

交叉：将种群中个体的部分基因与变异个体的部分基因按照规则交换，以提高种群的多样性．C为交叉概率，C值越大，交叉个体Ui(G)从变异个体Vi(G)中获得的基因越多，从而更接近变异个体，全局收敛的能力变强，但是会降低收敛速度；C值越小，全局收敛能力会越低，容易陷入局部最优．交叉过程可表示为

其中：r andj(0,1)为(0,1)之间的任意随机数，jrand为[1 ,D]内的随机整数．

选择：将所需要求解的问题换成适应度函数，越接近目标个体，适应度越小．将当前种群中个体的适应度 f(Xi(G))与相应的实验个体 f(Ui(G))的适应度相比较，如果实验个体的适应度小于或等于当前个体的适应度，则选择实验个体进入下一代种群．选择操作可表示为

其中 f (.)为适应度函数，函数的具体形式是由求解的问题决定的．

2 改进算法

差分进化算法的性能与结构参数值F和C的选择有很大程度上的依赖性，在进化过程中也存在陷入局部最优而导致收敛速度降低的问题．本文提出一种改进算法为基于反向学习和伯恩斯坦算子的差分进化算法(differential evolution algorithm based on opposition-based learning and Bernstain operator，BODE)．利用反向学习产生反向群体，扩大了种群的搜索空间，为找到潜在的最优个体提供更多机会，避免算法进化过程中容易陷入局部最优的问题；通过伯恩斯坦多项式随机产生结构参数并控制变异和交叉的过程，避免参数确定导致的试错过程，增强了个体的寻优能力，从而节省了搜索时间．

算法1：BODE算法

1. 输入：随机向量Xi．

2. 输出：个体的位置信息．

3. BEGIN．

4. 随机初始化种群．

5. 按照反向学习策略生成反向种群．

6. 计算种群中个体的适应值，选择适应值更好的个体作为下一代种群．

7. WHILE(终止条件是否满足)．

8. 由伯恩斯坦算子控制生成突变控制矩阵M．

9. 由伯恩斯坦算子控制生成进化步长F．

10. 生成实验个体．

11. 判断实验个体边界．

12. 由反向学习策略实现反向跳转．

13. 更新个体．

14. END WHILE．

15. 得到最优个体．

16. END．

基于反向学习和伯恩斯坦算子的差分进化算法具体流程如下：

(1)在初始化阶段，按照式(7)产生种群P，同时按照式(11)产生反向种群P′，在种群P和P′中选择适应值更好的个体组成初始种群．

(2)BODE通过式(12)和式(13)突变控制矩阵M．M的初始值由式(12)定义．

其中：随机数ρ的取值由式(2)产生，u向量为

permute(1 :D)函数可以随机交换(.)中元素的序列．

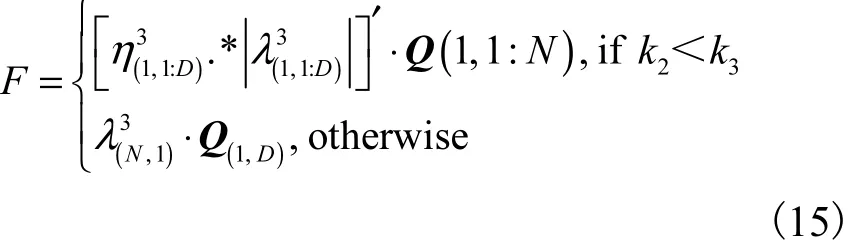
(3)在BODE中的进化步长F定义为其中：k2、k3、η和λ是在每次调用时产生的随机值，矩阵Q是全1矩阵．

(4)在BODE中，实验个体的生成阶段是一个随机交叉的过程，按照式(16)生成实验个体．

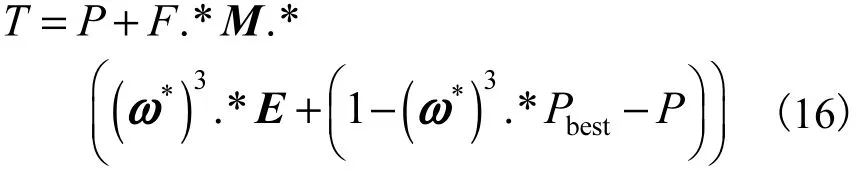
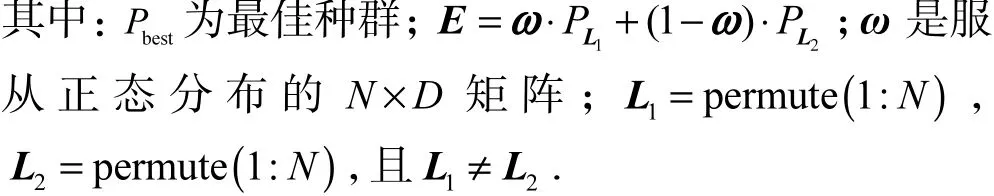
(5)如果实验个体超过了搜索范围，即Ti,j＜Lj或者Ti,j＞Uj，则个体采用式(17)进行更新，其中δ为(0,1)之间的随机数．(6)按照式(18)生成反向跳转的个体，Wmin和Wmax分别为当前种群中个体的最小值和最大值．

(7)分别求出实验个体、反向实验个体和原个体的适应度，按照式(10)选择适应度更好的个体组成新一代种群．

算法2：反向学习策略

3 实验仿真与结果分析

为了验证改进后算法的性能，选择了6种比较经典的测试函数，主要分为两大类，其中f1—f3为单峰函数，f4—f6为多峰函数，见表1．

表1 6种测试函数Tab. 1 Six benchmark functions

3.1 实验环境与参数设置

实验环境：Win 10操作系统，运行内存为8GB，运行软件为MATLAB 2017a．

基本参数设置：种群大小N＝48，种群个体的维度D＝30，最大迭代次数为5000次，各算法独立运行次数为20次，缩放因子F＝0.5，交叉概率C＝0.9．

3.2 仿真实验结果

BODE算法与DE算法、粒子群优化(particle swarm optimization，PSO)算法及BSD算法的比较结果见表2，其中PSO算法的实验结果来源于文献[15]．

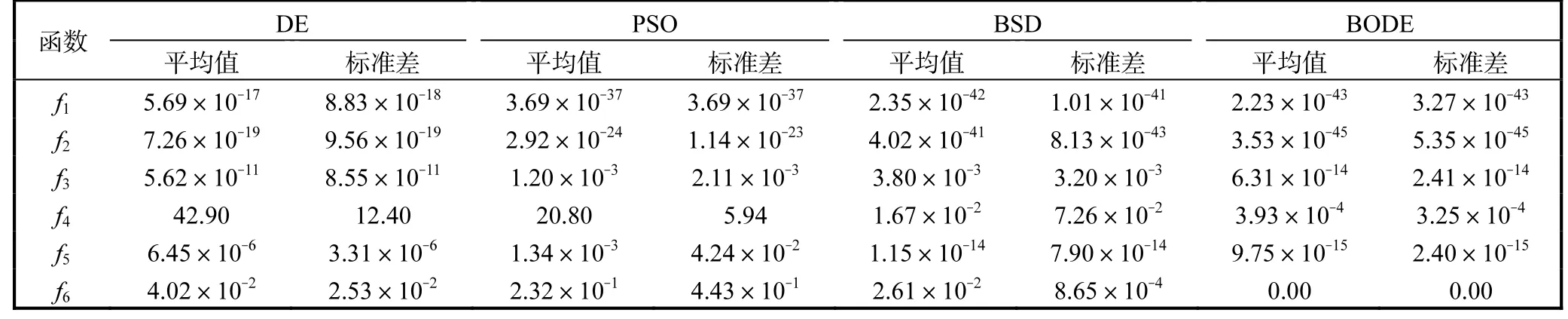
表2 4种算法在6个测试函数的实验结果Tab. 2 Experimental results of four algorithms on six benchmark functions

由表2可知，BODE算法不仅在单峰函数f1—f3中有绝对优势，在多峰函数f4—f6中也有明显优势．在单峰函数f1和f2中，BODE算法的收敛精度明显高于DE算法和PSO算法的；在函数f3中，BODE算法的收敛精度远高于PSO算法和BSD算法的．多峰函数f6在进化到5000次时，已经达到了收敛的最优值0．由此可知，加入反向学习策略和伯恩斯坦算子对增强算法的寻优能力以及提高算法的收敛精度有着重要作用．

测试函数结果对比如图2所示．

图2 测试函数结果对比Fig. 2 Comparison of bechmark functions

由图2可知，本文的BODE算法在收敛进度上与其他算法大致相同，但BODE算法的反向学习策略和伯恩斯坦算子可以加快收敛速度并提高收敛精度，有效地防止了算法的早熟现象，能够更快找到最优值．从图2(a)—图2(c)可知，BODE算法在处理单峰测试函数时，收敛精度和收敛速度优势明显．虽然f3没有表现优秀，但在整体上对算法的收敛性能有一定的帮助．由图2(d)—图2(f)可知，BODE算法在测试多峰函数时，能够解决多峰函数易于陷入局部最优的问题，帮助其快速找到全局最优值，且在收敛速度和精度上也表现突出．对易于陷入局部最优的函数f6，表现出了较强的搜索能力．

4 结 语

为了提升DE算法的性能，本文对算法中结构参数以及搜索策略进行改进，解决算法过早陷入局部最优的问题，以达到提高算法的收敛精度和速度、减少计算消耗的效果．通过采用反向学习策略增加种群的多样性，扩大搜索范围；而伯恩斯坦算子控制进化过程中的变异和交叉阶段，避免了参数的设定，增强了算法的搜索能力，提高了算法的收敛精度，使得算法更加高效．通过对国际标准测试函数的对比实验结果表明：BODE算法与其他算法相比有着更好的整体收敛性能，在进化阶段可以跳出局部最优，收敛速度更快，精度更高．测试函数对比图进一步说明了本文算法在收敛速度和收敛精度方面有更好的表现．后续工作可以在进化过程中加入更加高效的优化策略以及验证和分析改进后算法的性能这两方面进行，进一步提高算法的可靠性．