联合社区和影响节点的通用可扩展的链接预测
2022-03-01伍杰华程智锋
伍杰华,程智锋
(1.广东工贸职业技术学院 计算机与信息工程学院,广东 广州 510510; 2.广东工贸职业技术学院 教育部虚拟现实信息化协同创新中心,广东 广州 510510)
0 引 言
信息网络(information network)[1]是一种由实体和实体之间的关联组成的图结构。对信息网络的分析和理解是数据挖掘领域的其中一个主要研究方向,该研究方向又可以分为社区发现[2]、影响力节点识别[3]、链接预测[4]等。其中,社区发现(community detection)[2]是一个类似聚类的算法,旨在找出网络结构中的密集群组,使群组之间的链接稀疏,群组内部的链接紧密。该技术能够帮助科研人员在生物信息网络中找到功能类似的蛋白质结构[5];影响力节点识别(influential node identification)[3]目的是发现网络中最具备传播能力的节点。该技术能够理解和识别社交网络和舆情网络中谣言的传播机制和路径[6],改进供应链网络的物流运输方式[7]。链接预测(link prediction)[4]是预测尚未产生链接的节点之间是否会产生关联。社交网络中的朋友关系推荐、交通网络中的路线设计、生化网络中的食物链分析和科研合作网络中的科研工作者合作关系推荐等应用的实现均需以链接预测技术作为基础[8]。由于社区发现和影响力节点识别两种技术均需要对链接这一信息网络结构的核心组成部分进行分析,因此本文拟针对目前许多链接预测指标无法有效集成局部和全局结构信息对的问题,研究3个信息网络分析子领域之间的关联,设计一种高效的可扩展性的链接预测算法。
1 相关工作和问题定义
1.1 相关工作
链接预测问题由来已久,但随着其它领域工作的不断发展,该技术也在推陈出新,其中最主要的一个研究方向的基于网络结构的链接预测。比较经典的有基于局部共邻节点结构信息的算法(也可称为指标)((common neighbors,CN)、(adamic-adar,AA)、(preferential attachment,PA)、(resource allocation,RA)等等)[8],基于半全局路径或随机游走结构的算法((local path,LP)[9]、Katz[9]、(return random walk,RRW)[10]等等)。近年来,一些工作尝试引入局部密集结构到链接预测算法中,例如Wu等[11]提出了一种基于聚类系数(cluster coefficient,CC)的链接预测算法,该算法引入共邻结点的聚类系数反映链接生成的机制。Chen等[12]把聚类系数的定义嵌入朴素贝叶斯模型中,取得更好的预测效果。此外,Wu等[13]还提出一种集成节点和链接聚类信息的算法(node and link clustering,NLC),在top-L测试中取得比基准算法更好的性能。但是上述算法提取的仅仅是局部链接密集度信息。基于该信息定义的相似度指标尽管结构简单、时间复杂度低,但是没有充分引入网络的经典密集度结构(社区结构)计算其影响力,而且不同规模社区之间存在差异性,直接把社区信息适配到相似度指标会造成信息不完整和损失。
与此同时,尽管社区反映了部分网页的全局信息,但是相关工作表明,一些使用全局结构信息的预测算法(SPM[14]、LR[15])的效果是更优的,但是它们运行速度慢,内存占用率高,如何在划分社区的基础上引入全局信息保持运行效率是其中的关键。近期,一些工作尝试从影响力节点识别方法设计链接预测算法。相关综述指出[3],影响力节点识别方法目的是在网络中找出信息传播中产生影响范围最大最广的节点或者节点集合。该方法有效描述了节点在全局网络结构中的许多动态活动,例如传染病暴发、谣言传播等等。这些方法为每个信息传播过程中经过的节点赋予一个全局的影响力函数度量节点的影响力,相关工作[16]把它作为得分加入到链接预测相似度得分公式中,并取得较好的效果。图1用网络图描述了这一问题。其中a,b是两待预测节点,它们之间的虚线表示潜在需要预测的链接,实线表示存在链接。该结构划分成左右两个社区A和B,节点颜色的深浅表示该节点的影响力大小,颜色越深,影响力则越大。很明显,在社区划分状态下不同共邻节点的影响力是会对链接预测结果产生影响的。
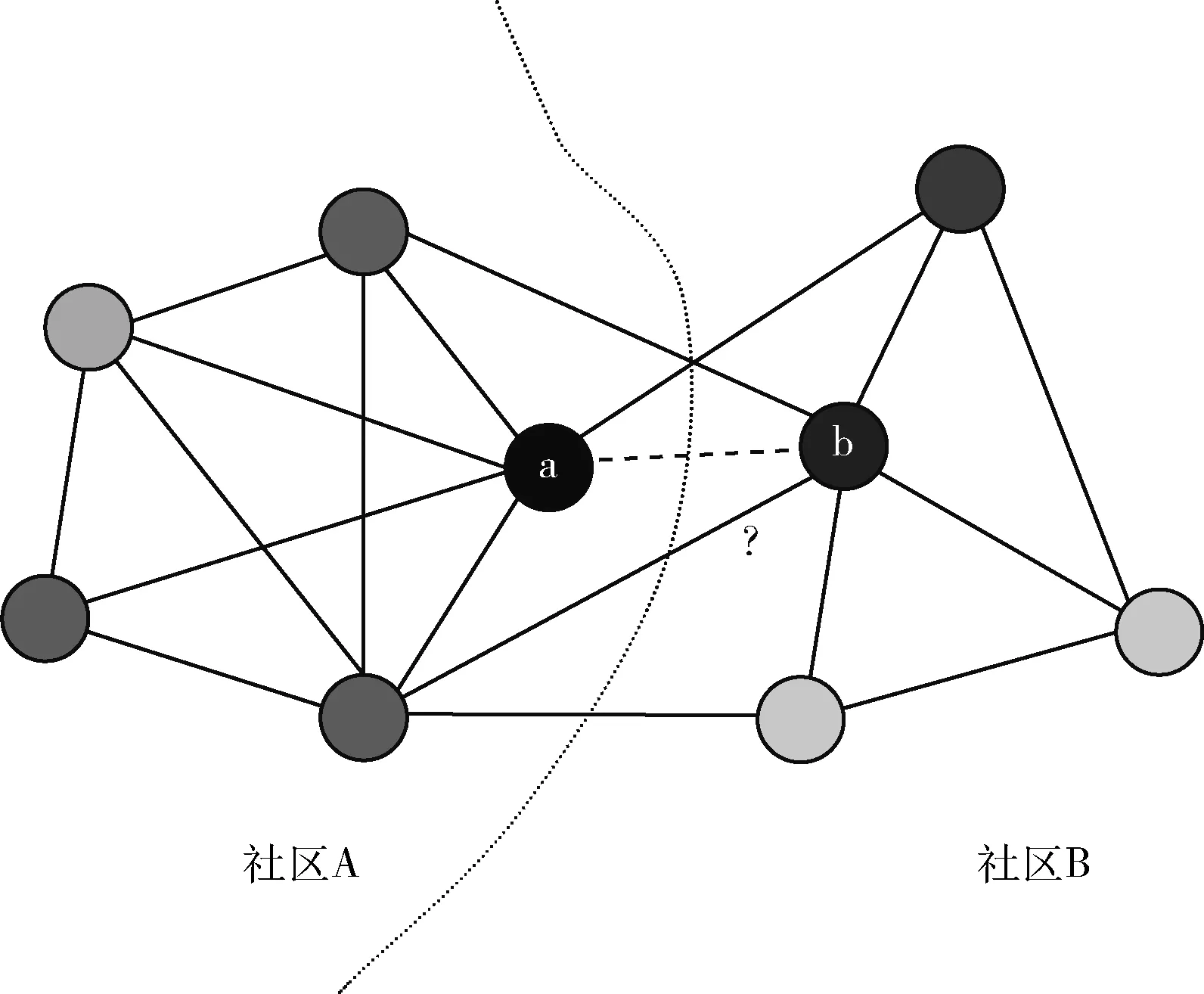
图1 算法结构模型
因此,本文提出一个可扩展性的融合社区发现和影响力节点识别两种技术的链接预测算法。该算法首先提取各节点的影响力函数得分(节点影响力),然后采用社区发现算法划分社区,运用社区参与度的概念计算不同规模社区内共邻节点对链接生成的影响得分(社区影响力),最后把上述得分集成到一个统一的模型中。同时,还讨论了不同社区发现算法和多个类型的影响力得分计算函数的性能。在各类型真实信息网络的实验结果表明,算法复杂度较低,是通用且可扩展的,同时预测的性能优于基准算法。
1.2 问题定义
给定一个信息网络G=(V,E,C), 其中V和E分别是节点和链接的集合,C是网络划分成k个社区的集合,其中C={c1,c2,c3…ck},k>2, 同时ck表示第k个社区,c(i) 表示节点i所处的社区,I(i) 则表示该节点的影响力得分。此外,给定u和v两个节点,N(u) 表示节点u的邻接节点集合。共邻节点则定义为u和v邻接节点集合N(u) 和N(v) 的交集,表示为:CN(u,v)=N(u)∩N(v)。
链接预测的任务可描述成如下的流程:①把G按照比例r划分成训练集、预测集并划分社区,计算社区影响力和节点影响力。②计算训练集中每对节点对的相似度得分。③和预测集比较前N个相似度最大值计算评估指标,获取预测结果。
2 算法模型
相似度表示两节点关系的紧密程度,计算两个潜在节点的相似度是基于网络结构链接预测方法的最主要方式。大部分相似度链接预测方法基于局部共邻节点构建,这是因为共邻节点信息是影响链接生成最直观的结构,例如在社交网络中,节点u和v表示目前不存在关系的两个用户,链接表示他们之间的朋友、关注关系,共邻节点表示和u、v均存在朋友关系的共同朋友。很明显,两个用户的共同朋友越多,他们产生朋友关系的可能性就越高。因此,许多相似度算法基于共邻节点结构展开,它们的通用表达形式为[17]

(1)
其中,ω是共邻节点,s(u,v) 表示两节点之间的相似度值,一般相似度值越高,u和v之间产生链接的可能性则越高。f(ω) 表示由共邻节点结构属性构成的得分函数。在许多经典相似度指标中,f(ω) 可以表示为局部的共邻节点数目、度、度的对数和聚类系数等结构,也可以定义为随机森林、邻接矩阵等全局结构。
为了使得分函数更好反映网络的局部和全局信息,在本文工作中拟保留式(1)中的f(ω) 表示局部社区影响力函数,同时添加1/g(ω) 表示全局节点影响力函数的倒数,并定义如下
(2)
需要注意的是,节点影响力得分放在了分母。这是因为在相似度得分中,共邻节点影响力大,其对链接生成的影响成反比。
2.1 社区影响力函数
信息网络拓扑结构和其表示的实体结构相似,都是由若干个节点之间的链接紧密的“社区”或“社团”构成。根据社区属性可知,社区结构内部的链接往往比社区之间的关系要紧密。因此社区结构对于理解链接是如何形成是非常重要的。一些工作指出[18],由于社区内部链接密度高,新链接倾向于在内部产生,一些工作则认为,社区之间链接是信息跨领域传播的重要路径,新链接也有很大概率在此产生。由图1可见,待预测节点a,b对的共邻节点可能在社区A,也可能在社区B,共邻节点的邻接节点也可能分属不同的社区。由于社区A和社区B内部的链接密度不同,构建基于共邻节点的相似度得分函数需要把该属性考虑进去。况且两个社区的规模也不一致,如何区别不同共邻节点的贡献也需要解决。
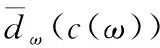
(3)
可以看出,ω的邻接度和越大,kω(c(ω)) 的值便越大,则在计算相似度得分时它的贡献就越大。
第二步,找到和待预测节点属于不同社区的共邻节点,计算其贡献。由于共邻节点和待预测节点不属于相同社区,根据社区理论其链接相对稀疏,因此贡献通过ω的参与系数pω(c(ω)) 来定义,其公式是
(4)
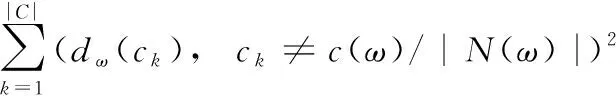
(5)
当ck≠c(ω) 时,pω(ck)=0代表共邻节点的邻接节点均在该节点所处社区的内部。采用单位减法的含义在于根据划分社区的属性,社区内部链接生成的概率比社区之间的要高。因此,局部的社区影响力函数为
根据差异化共邻节点贡献的目的,算法需要强调(增大)社区内部共邻节点的影响同时惩罚(减少)社区外部共邻节点的影响,同时在社区内部和社区之间的链接生成找到平衡。因此,后者的乘积采用负数,且共邻节点的参与系数越大,其对相似度得分的贡献越小。
2.2 影响力节点识别函数
尽管引入社区属性,但是上述算法均从局部角度建立公式,并没有考虑网络的全局结构。作者最新的工作[16]尝试使用影响力节点识别指标表示g(ω), 在许多数据集上均取得了较好的效果。但是该指标缺少局部信息,因此本节结合局部社区属性或局部密集度属性提升预测的准确度,进一步扩展该指标。
影响力节点识别(又称关键节点识别)的核心是如何度量节点的影响力,一般来说定义为该节点与网络中的其它节点具备不同的信息传播能力(重要性,显著性),用网络的属性结构可以表示为度、局部中心性、核度、混合度和随机游走等等。为了验证算法的适配性和可扩展性,本部分引入几个新颖的、经典的影响力节点识别指标定义g(ω), 并嵌入到链接预测相似度框架中。
(1)Katz向量中心性(Katz eigenvector centrality,EC)[19]。Katz是在特征向量中心性的基础上提出的,特征向量中心性把邻接矩阵的最大特征值的特征向量作为中心性度量值,但是不适应当图中出现有向无环图的情况,Katz在此提出了一个改进方法,即每个节点初始就有一个中心度值。节点ω的重要性g(ω) 可表示为
(6)
其中,b=1, 衰减因子c=0.5λmax,λmax是邻接矩阵的最大特征值。
(2)PageRank(PR)[20]。PageRank是一个基于随机游走的影响力节点识别指标。该指标是一个搜索算法,它借鉴了学术界评判学术论文重要性的通用方法——引用,通过网页之间的链接关系给网页的级别或者重要性进行排序,并把排序的结果作为搜索结果提供给用户。随着网络科学研究的不断深入,PageRank作为影响力节点识别,已经广泛用于社交网络关键用户发现、航空网络枢纽识别等多个领域。该指标ω在t时间的重要性gt(ω) 可表示为

(7)
其中,γ是阻尼系数,表示从某个节点跳转到下一个节点的概率,一般设置为γ=0.15, (1-γ) 则表示随机跳转到其它节点的概率。ki表示第i个节点的入度,N为网络总节点数,aiω表示节点ω到i有一条路径,取值为1,如不存在则取值为0;当ki=0时,σkI,0=1。
(3)LeaderRank(LR)[21]。该指标是对PageRank的一种改进。添加了一个基础节点ground node指向所有节点,保证每个节点的度均大于1,其依据在于邻接度低的节点访问基础节点的概率比邻接度高的节点访问基础节点的概率要大。该指标ω的重要性gt(ω) 可表示为
(8)
(4)ClusterRank(CR)[22]。近期,相关工作在科学家合作网络等真实数据集上的实验验证了聚类系数对于节点获取新的邻居节点是不利的。同时它们认为在影响力节点识别问题中,聚类系数值越大,对于一个节点的影响力来说,是一个负面的因素。该指标ω的重要性g(ω) 可表示为
(9)
ccω表示节点ω的聚类系数,h(ccω) 是把聚类系数作为参数的函数,一般用指数函数h(ccω)=10-ccω表示。特别需要指出的是,g(ω) 和上一小节讨论的f(ω) 均是以共邻节点ω作为参数的函数,因此可以适配任意包含共邻节点结构信息的特征,因此算法的相似度模型对不同的影响力节点识别函数是通用的。
2.3 可扩展性讨论
2.1小节中的社区影响力函数尽管在一定程度上能够表示共邻节点的局部影响,但是其定义和概念也是全局的,尤其对于稀疏网络,该影响力很难给予相似度得分贡献。因此在本小节中探讨加入更具备局部属性的影响力得分到f(ω) 中,验证算法的可扩展性和鲁棒性。
2.3.1 局部密集度影响的可扩展性
(1)聚类系数。聚类系数是网络局部结构中节点聚集程度的度量,其具体被定义为任何节点ω作为其中一个顶点参与形成的三角形数目tω与其最大可能参与形成的三角形数目之间的比率
(10)
如果ccω=0表示该节点没有邻居节点,ccω=1则表示所有邻接节点均紧密相连。
(2)局部社区范式(local community paradigm,LCP)[23]。LCP总结了局部结构中链接互连的多种模式,提出了一系列结构简单且高效的局部密集度指标,文中选取了实验效果表现最好的(Cannistraci resource allocation,CRA),其定义为
(11)
其中,γ(ω) 表示ω集合中也是u和v共邻节点的数目。
2.3.2 不同模块度社区影响的可扩展性
模块度刻画社区的紧密程度,是一种经典的衡量社区发现算法质量的指标。不同的模块度和社区数目决定节点相邻局部结构的紧密程度,也会导致不同的相似度得分。为了验证提出模型在不同社区发现算法都是适用的,本小节通过综述[24,25]介绍另外两个经典的模块度社区发现算法:
(1)F-N(Fast Newman)算法。Newman在该工作中首次定义了模块度(Modularity)概念并提出对应的社区发现算法F-N。该算法的思想是:当进行社区划分时,将结点加入它的某个邻接节点所在的社区中,如果能够提升当前社区结构模块度,则进行迭代划分,直至模块度不再收敛为止。
(2)多尺度贪婪算法。该算法由社区发现领域的知名学者Erwan Le Martelot提出,该算法除了采用模块度定义外,还使用了稳定性(Stability)概念度量划分的质量,然后使用一个多尺度的贪婪算法最大化模块度和稳定性,取得较好的划分性能。
2.4 通用性讨论
前文介绍算法主要针对无权的信息网络建立,而在现实世界中,存在节点之间的链接强度不一的信息网络。为了验证算法的通用性,本小节将提出的算法拓展到加权网络的链接预测任务中。从式(2)可以看出,其中一个核心模块是引入影响力节点识别函数定义g(ω)。 因此,加权网络通用性的验证思路是引入链接的加权信息,将无权的节点影响力识别指标变成加权形式。由于并没有相关文献给出每一种影响节点识别指标的加权形式,因此一般的做法是通过将邻接矩阵替换为加权邻接矩阵来计算各指标的加权影响力,对应的加权指标称为WEC(Weighted EC)、WPR(Weighted PR)、WLR(Weighted LR)和WCR(Weighted CR),其中Weighted表示加权的含义。
3 实验结果与分析
3.1 实验准备
本文实验采用Konect平台[26]提供的不同类型的公共数据集,它们的名称和属性显示在表1中,其中N是节点,E是链接,CC是聚类系数,K是平均度,Community 1和Community 2分别是采用上述两种社区划分算法划分的社区数目,-表示无法划分社区。

表1 数据集属性
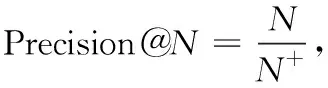
本实验采用以下5类方法对上述数据集开展实验:
方法1:基于局部共邻节点结构信息算法:AA。
方法2:基于局部密集和社区结构算法:CC、LNBAA(Local Naïve Bayse Adamic-Adar)、NLC。
方法3:基于路径的算法:Katz、LP。
方法4:新近提出的基于全局邻接矩阵变换的链接预测方法:(structural perturbation method,SPM)、(matrix completion,MC)。
方法5:本文提出算法:(eigenvector centrality link prediction,ECLP)、(pagerank link prediction,PRLP)、(leaderrank link prediction,LRLP)、(clusterrank link prediction,CRLP)。
同时,各算法的加权形式即在原始算法名称前添加字母W,表示weighted。所有实验都是在一台具有1.5 GHz CPU内核和8 GB RAM的计算机通过Matlab语言单线程实现的。
3.2 实验结果
为了验证本文提出框架的性能,本部分实验分成两部分进行比较。第一组实验把社区影响力赋予f(ω), 把4种节点影响力赋予g(ω), 计算该框架下各指标的性能。从表2的结果中可以得出如下结论:
(1)从总体上看,对于绝大多数数据集,提出框架的几个指标所表示的链接预测效果明显要好于其它基准算法。在Macaca和Corecipient数据集中,尽管最佳效果分别是LNBAA和NLC,但第2-第5名次优值均是本文提出的指标。这表示g(ω) 是通用的可以嵌入不同的影响力节点指标。此外,我们在社区1下计算4类方法在各数据集中所有Precision值的平均值,第四类方法的预测准确度比第一类方法到第3类方法分别提高了4.36%、2.77%、16.62%。上述的结果不仅验证局部函数的通用性,也充分体现了将两个影响力函数考虑进去能够得到性能更优的指标。
(2)从不同社区算法下预测效果来看,最优和次优的指标基本上均是本文提出的指标,且其排名类似。除此之外,我们还测试了另外几个社区发现算法,发现各算法的表现情况基本一致,由于版面关系在此不再一一列出。由此可以看出,框架是可扩展的,适配于任何社区发现算法。此外,尽管不同的社区划分算法划分的社区数目基本一致,但比较各数据集在不同社区发现下的效果,可以看出F-N算法的效果从整体上要更优,具体原因可能是该社区划分的模块度更大,社区之间关系更加稀疏,社区影响力更能给予链接相似度得分贡献。
为进一步验证框架的鲁棒性和可扩展性,第二组实验在第一组的基础上把2.3小节中两个局部密集度影响赋予f(ω), 计算该框架下各指标的性能,结果在表3中所示。从对比结果可以发现:
(1)和第一组实验一样,无论在哪种社区划分和哪类密集度度量下,CRLP指标的预测性能最好。同时,有提出的指标在所有数据集中基本维持和实验一一致的性能。
(2)更重要的是,在第一组实验中Corecipient数据集各指标的预测效果均在0.7以下,低于NLC的最优值。但是一旦引入了CC和CRA度量,4个指标的预测效果均提升了至少6%,最高达到8%。该组实验说明了局部密集度度量能在部分数据集提升预测性能并不影响原有的社区属性和影响力节点贡献,也再一次验证了提出的框架是可扩展和通用的。
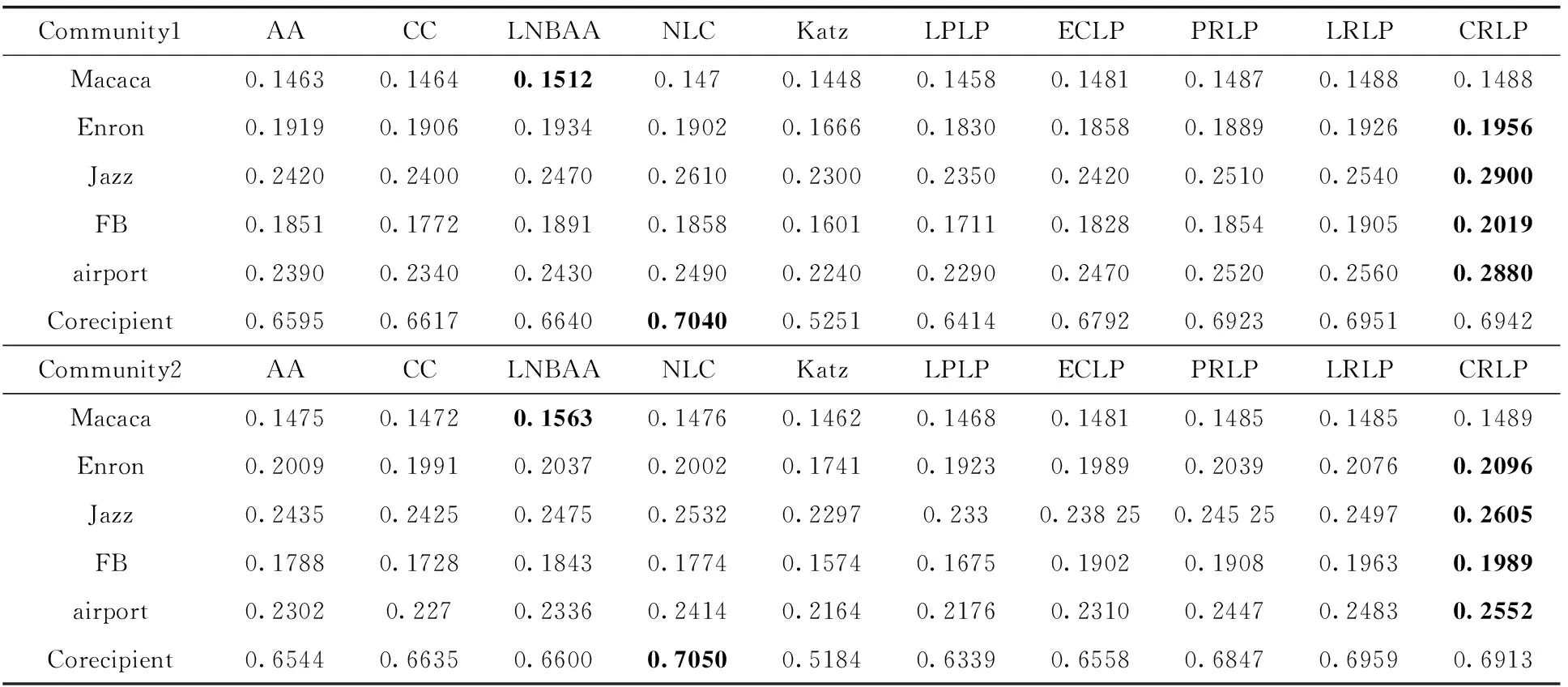
表2 各指标的算法性能

表3 局部社区密集度可扩展性分析
3.3 实验分析
为了进一步验证算法的精度、敏感和稳定性,本部分进行了两部分的拓展实验。第一部分实验尝试调节随机抽取数据作为训练集的比例,从0.6采取0.02的步长逐步调高为0.9,输出每一步各指标下不同数据集下的预测值,这里把局部密集度影响赋予f(ω)。 为了更加清晰地比较,实验在基准方法和提出方法均选择2个性能最好的指标绘图。FB和Corecipient数据集下的效果如图2所示,其中Corecipient-com1表示对Corecipient数据集采用社区发现算法1,CRLP表示采用CR的链接预测指标。可以看出,方法4中的2个指标在大多数情况下均在右上方,尤其表示CRLP的曲线始终在右上方,这和上一小节的实验相吻合,表明提出的指标对训练规模是不敏感的,预测性能是稳定的。以图2(c)为例,当训练集的比例从0.6到0.7时,各指标的预测值均相差无几,当横坐标变成0.8时,CRLP仍然是0.993,AA、CC、LNBAA、NLC、Katz、LP、EC、PR、LR分别变成0.969、0.974、0.971、0.977、0.856、0.968、0.962、0.962、0.97。然后比例渐渐升到0.85,这时LRLP效果逐渐变优,和CRLP基本一致,均比其它基准算法要优。第二部分实验调整Precision@N中的N值,从N=500采取50的步长逐步调高为N=1000,输出每一步各指标下不同数据集下的预测值,这部分使用原始的f(ω)。 和第一部分实验一致在基准方法和提出方法均选择2个性能最好的指标绘图,FB和Corecipient数据集下的实验如图3所示。从结果可以看出,子图(a),(b),(c)的每一步上位居右上角的曲线均是本文提出的指标,其在N值变化下预测效果是稳定的。而子图(d)中在N>700后最优的指标是NLC,上述结果一方面和表1的相对应,一方面也体现提出指标在N<700时候性能是非常好的。该部分实验和基于全局邻接矩阵变幻的SPM和MC算法相比较,其中SPM基于网络结构一致性(structural consistence)这一特性构建,该指标表示结构一致性越强的结构存在的链接越容易预测;MC则引入矩阵缺失信息补全的概念进行预测。在各数据集上的预测时间及结果如图4、图5所示。从结果可以看出,尽管各数据集最优的预测效果出现在MC算法中,但是PRLP和LRLP和其相差不远,且它们的预测性能均比SPM要高许多(在Jazz和Airport数据集上至少要高80%)。更值得注意的是:PRLP和LRLP的运行时间比SPM和MC要低许多,例如在Jazz数据集中,PRLP和LRLP运行时间仅仅需要1.3 s~1.6 s,而SPM和MC则分别达到9.2 s和5.6 s。这充分表明,本文提出的算法能在保证较高预测精确度的同时缩短运行时间,对更大规模更加密集的网络预测场景产生更优的效果。
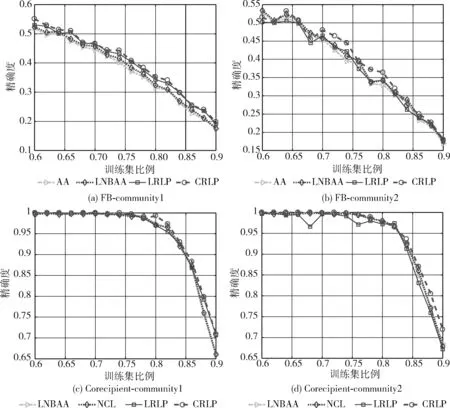
图2 FB和Corecipient数据训练集变化下的预测效果
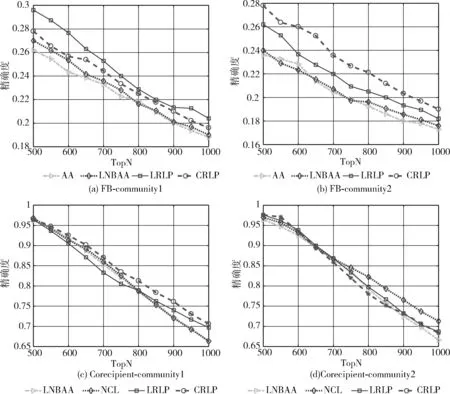
图3 FB和Corecipient数据TopN变化下的预测效果
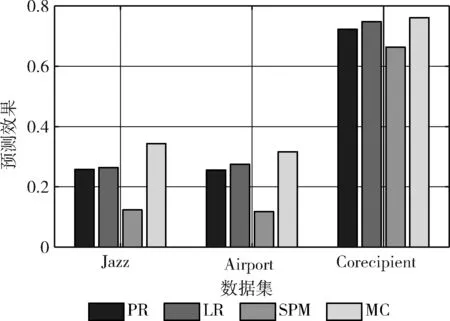
图4 和全局指标比较的预测效果
为了综合考虑不同Precision@N下的预测性能,本文还在加权网络数据集上进行了两组不同的实验,结果见表4。从实验结果可以看出,各数据集下N=1000的预测效果要比N=1500的预测效果要优,这是符合链接预测实验的一般规律的,表明实验结果是有效的。更重要的是,本文提出的4类算法相比基准算法普遍能得到较好的效果,在WECLP、WPRLP、WLRLP和WCRLP各数据集的平均预测准确度是34.233%、32.767%、16.7%和21.933%,普遍要高于WAA、WLNBAA、WCC和WLP的14.967%、23.4%、16.333%和13.4%,其中最优的效果均出现在WEC算法中。这说明尽管引入额外的加权信息,但是本文提出框架的几个算法均能够在各个加权数据集上都有优良的表现,也反映出框架对不同的网络类型是通用的。
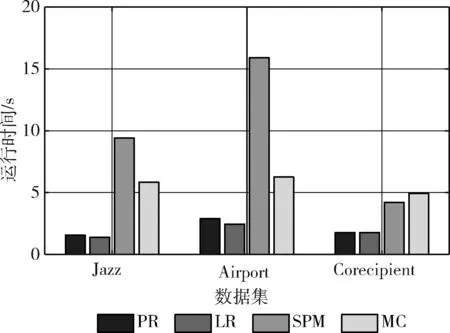
图5 和全局指标比较的运行时间
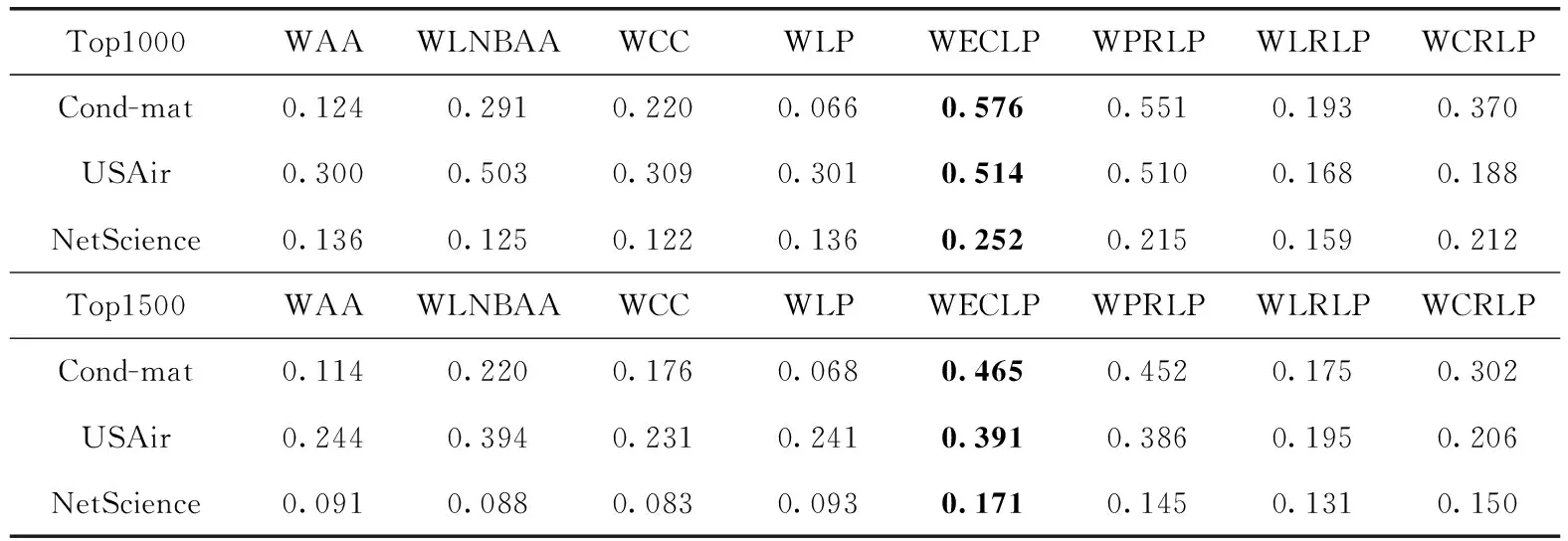
表4 加权算法的预测效果对比
4 结束语
本文主要介绍了一个融合社区影响力和节点影响力的链接预测算法。该算法集成了局部密集度信息,有效分析了不同社区结构对链接相似度的影响,同时充分考虑了节点影响力这一全局属性,结合上述因素提出了一个通用的、可扩展性强的模型。实验结果验证了模型的有效性。
下一步工作中,我们将探索其它局部和全局因素对链接相似度的影响,例如网络动态演化模式、模态(motifs)等等。此外,如何把本文方法拓展到异质、多维信息网络也是下一步需要研究的方向。
