基于SAP2000的透水桩坝内力分析模型实现

胡 正,牛万宏,马奇豪

(河南黄河勘测规划设计研究院有限公司，河南 郑州 450003)

近年来，随着工程建设规模的扩大，各种类型的支挡结构的应用日益广泛，在现行《建筑基坑支护技术规程》(JGJ 120—2012)[1]等相关规范中对支挡结构的内力计算主要采用弹性地基梁法，与传统的内力平衡经典法不同的是，该方法将支挡结构当作垂直放置的梁，开挖面以下土体部分简化为反力弹性支座。该方法综合考虑了土、支挡结构以及支撑锚杆的共同作用，方法简单，目前在实际工程中得到广泛应用。

黄河下游河势游荡多变，河道整治的控导工程通过对洪水的挡、挑、顺等方式，引导和控制洪水按规划的流路演进。混凝土桩由于布置灵活，可一次性施工至最大冲刷深度范围以下的稳定地层中，具有坝前抗冲刷，坝后落淤造滩相结合的特点，开始在河道整治工程中得到一定应用。耿明全等[2]对该坝型原理及应用工艺进行了研究；刘筠等[3-5]对潜坝的冲刷深度、内力分布等进行了分析研究；姚文艺等[6]对潜坝桩体控导效果进行了模型试验研究；王普庆[7]对透水桩坝桩后落淤情况进行了研究。

由于黄河下游的游荡性河势复杂多变的特点，在不同的河道运行条件下，计算工况较为复杂，李永新等[8]针对透水桩坝内力分析研究采用FLAC3D等数值计算软件建立三维非线性数值模型，利用接触元模拟桩土相互作用进行内力计算分析。FLAC3D等大型三维数值计算软件具有适用性广的优势，但存在前处理功能弱、运行效率低、建模烦琐等问题，SAP2000为通用结构分析软件，具有适用性广、建模便捷、后处理方便等优势，可提高工作效率。本文通过工程案例对比计算分析，探讨通过SAP2000软件建立弹性地基梁模型对支挡结构以及透水桩坝进行内力分析的可行性，为透水桩坝的设计计算提供参考。

1 内力分析模型建立

1.1 概况

黄河下游地区地貌主要属黄河冲积平原，岩性主要为粉土、砂土等松软土层，且受水流冲刷影响较大，主要是靠插入土中的悬臂桩体抵抗水平力实现导流、控导河势的作用。为简化计算，假定各土层为均质土层，并假设各工况下的冲刷一次完成。桩型采用预制管桩，预制管桩外径0.6 m，桩内径0.3 m，桩净距0.3 m，桩身混凝土等级采用C60。当管桩用作不透水支挡结构时，管桩主要受桩体移动产生的主动土压力和被动土压力作用；当管桩用作透水桩坝时，管桩主要受静水压力、动水压力和桩体移动产生的主动土压力和被动土压力作用。

1.2 计算模型及相关参数

对承受水平荷载的排桩视为竖向弹性地基梁，桩侧土反力采用杆单元侧向弹簧系数模拟，桩侧土水平反力系数采用“m”法计算，支挡结构内侧土的水平反力系数按式(1)计算：

ks=m(z-h)

(1)

作用在挡土构件上的分布图反力符合式(2)规定：

ps=ksv+ps 0

(2)

式中：ks为水平反力系数，kN/m3;m为水平反力系数比例系数，kN/m4；z为计算点距地面的深度，m;h为当前工况阶段下的基坑开挖深度，m;ps0为初始分布土反力，kPa；ps为分布土反力，kPa；v为挡土构件分布土反力计算点水平位移值，m。地层主要为砂壤土及细砂，主要土层参数：砂壤土层为c=11.4 kPa，φ=26.5°；细砂层为c=0 kPa，φ=30°。

1.3 水土压力

(1)土压力。支挡结构所承受的土压力与其位移关系较大，支挡结构的变形使土体产生了应力重分布，因此作用在支挡结构上的土压力是一个动态变化的过程，实际上的支挡结构与周围土体是一个复杂的非线性空间体系。本项目近似满足半无限空间体假定，各土层均为水平分布，水土压力分布如图1所示。

(2)动水压力。根据《公路桥涵设计通用规范》(JTD D60—2015)[9]规定，动水压力标准值按式(3)计算：

(3)

式中：Fw为流水压力标准值，kN；K为形状系数，圆形取K=0.8；A为流水截面面积，m2;γ为流水比重，kN/m3;V为设计流速,m/s；g为重力加速度，取9.81 m/s2。

(3)静水压力。静水压力根据pw=0.5γwH2计算，其中取γw=10 kN/m3进行计算。考虑到河流中坝前水位的壅高，因此在计算中对于不同流速下桩坝前后水位需考虑一定的水位差。

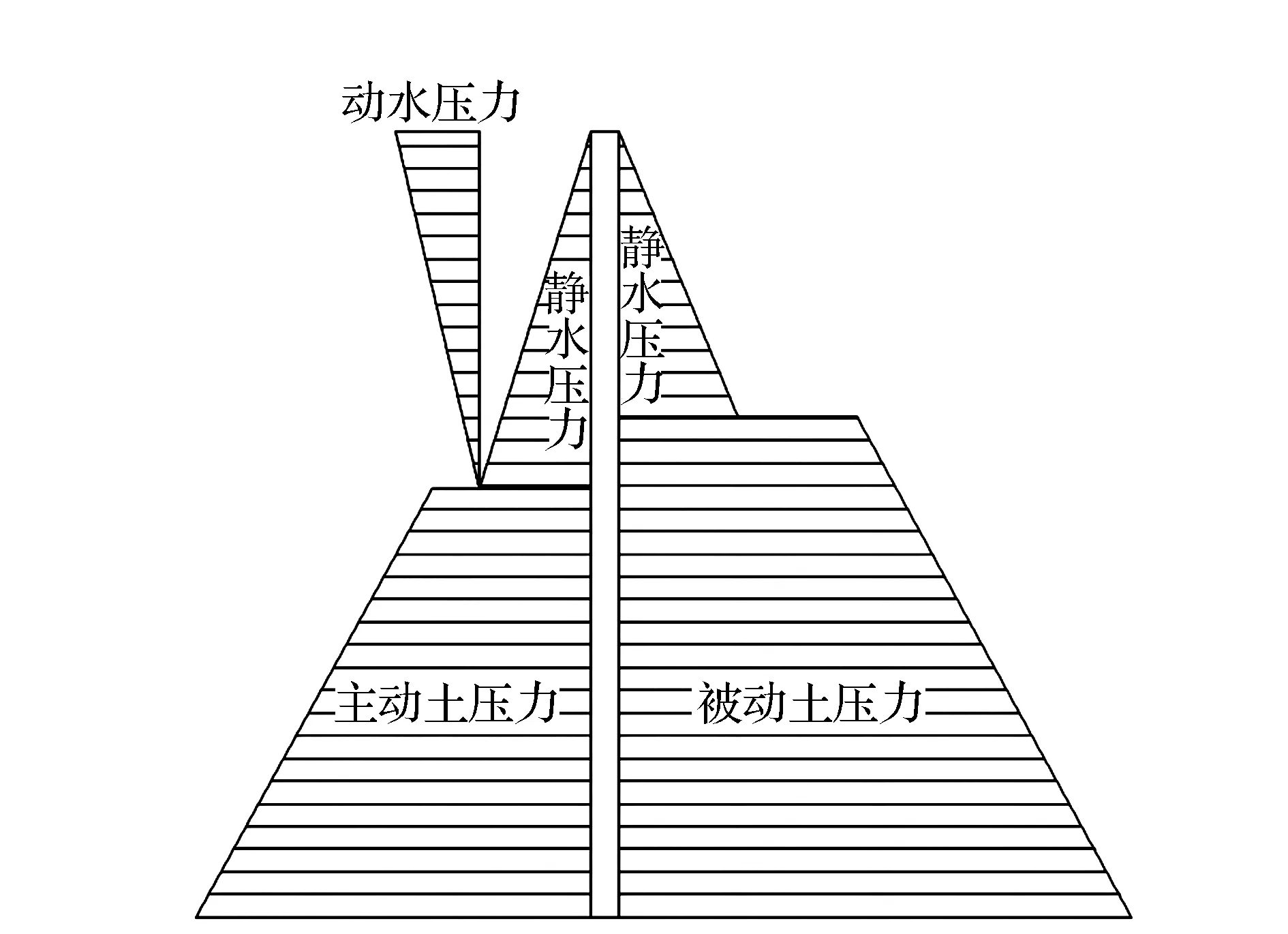
图1 桩体受力示意图

1.4 计算工况选取

透水桩坝在河道整治中主要是起控导水流，促进滩槽水沙交换、淤高其后滩地的作用。要达到桩前控水抗冲，桩后落淤造滩的作用需要综合水流黏滞特性、流速分布、透水桩坝的消能作用以及水流运动形态和河道特性等多种因素的影响。为简化计算，假定各土层均为均质，并且假设各工况中冲刷一次完成，考虑到黄河下游河道近年来的运行实际，共设置以下五种工况进行分析，本文所采用的计算工况详见表1。

表1 工况特征表

1.5 内力计算方法

目前对于承受水平方向荷载桩基的内力计算主要采用弹性地基梁法，通过对梁的挠曲微分方程求解，进而计算出桩身的弯矩和剪力。

2 计算结果分析

2.1 工况一和工况二

两种计算工况分别为：工况一桩后土体(细砂)高程在冲刷线以上1.0 m；工况二：桩后土体(细砂)都平冲刷线。在工况一和工况二条件下，河道流量为800 m3/s，冲刷深度为8.0 m，桩坝前后水位差0.2 m，动水压力系数采用桩前水深计算。

计算结果如图3、图4所示，采用弹性地基梁模型对桩坝内力进行计算时，管桩在动水压力、桩前后静水压力差及土压力的共同作用下，管桩上部向河床方向移动，桩顶位移在桩后土体高程在冲刷线以上1 m时达24.62 mm，当桩前后土体平冲刷线时，桩顶位移达43.03 mm；两种工况桩体最大弯矩分别为113.73 kN·m、135.85 kN·m，最大剪力分别为45.24 kN、67.53 kN。整体相差不大，工况二条件下桩身内力、变形均略大于工况一。

图3 工况一内力位移数值计算结果

图4 工况二内力位移数值计算结果

2.2 工况三和工况四

两种计算工况分别为：工况三桩后土体(细砂)高程在冲刷线以上1.5 m；工况四：桩后土体(细砂)都平冲刷线。在工况三和工况四条件下，河道流量为4000 m3/s，冲刷深度为12.0 m，桩坝前后水位差0.3 m，动水压力系数采用桩前水深计算。

计算结果如图5、图6所示，采用弹性地基梁模型对桩坝内力进行计算时，管桩在动水压力、桩前后静水压力差及土压力的共同作用下，管桩上部向河床方向移动，桩顶位移在桩后土体高程在冲刷线以上1.5 m时达113.35 mm，当桩后土体平冲刷线时，桩顶位移达168.28 mm；两种工况桩体最大弯矩分别为352.24 kN·m、436.86 kN·m，最大剪力分别为102.38 kN、125.30 kN，相差较大，整体上仍是工况四条件下桩身内力、变形均大于工况三。

图5 工况三内力位移数值计算结果

图6 工况四内力位移数值计算结果

2.3 工况五

工况五桩后土体(砂壤土及细砂)高程平桩顶，桩前深度为10.0 m，计算中不考虑动水压力，桩前后水位持平，利用理正软件进行对比计算。计算所得弯矩及剪力见表2所示。

表2 10 m深度桩坝内力位移计算对比表

2.4 综合分析

(1)在相同工况条件下，采用SAP2000弹性地基梁模型分别对流量为800 m3/s中小水工况和4000 m3/s的大水工况的桩身内力位移等进行了计算，根据算例计算结果，与文献[8]相同工况条件下的计算结果进行对比，两种软件的计算结果较为接近，同时桩身最大弯矩作用点深度及剪力零点位置均较为一致。当采用理正软件对工况五悬臂桩内力进行计算时所得计算结果也与SAP2000弹性地基梁模型计算结果基本吻合。

(2)当冲刷深度增加时，桩坝桩身位移、内力会随冲刷深度的增加而增大，同时当冲刷深度增加时，桩坝后落淤时对桩坝桩身位移、内力影响程度也随着增大，因此桩后相同的落淤深度条件下当冲刷深度增加时，桩身内力位移降低幅度越大。

(3)根据同一冲刷深度条件下的桩坝内力计算结果来看，当桩坝背河滩面高程相比较桩前临河侧高1.0～1.5 m时，桩顶位移、桩体最大弯矩、桩体最大剪力等均有不同程度降低，主要原因是桩后土体产生的土压力和静水压力抵消掉一部分桩前后静水压力差与动水压力。黄河近年来主要为中小水流量运行状态，根据相关研究成果，在中小水流量形态下桩后落淤一般小于2.0 m，当桩后落淤厚度增加在一定范围内时桩身内力会有一定程度降低，但桩坝嵌固深度会增大，设计时应按不同工况特性分别计算嵌固深度进行复核。

3 结 论

(1)经过多种数值计算软件计算结果对比分析,SAP2000弹性地基梁模型可用于对复杂工况条件下的悬臂桩桩身内力分析计算，与其他数值计算设计软件计算结果相比，计算结果较为接近，相比较其他三维数值计算软件，SAP2000在提高工作效率上具有一定优势。

(2)桩后落淤会使桩体自身受河道动静水压力时产生的桩身内力有一定程度降低，当桩前临河侧冲刷深度越深时，这种作用越明显。

(3)桩坝桩身内力受冲刷深度影响较大，当冲刷深度增加时，桩坝桩身位移、内力会随冲刷深度的增加而增大，在桩坝运行工况中，当桩后落淤厚度增加在一定范围内时桩身内力会有一定程度降低，但桩坝嵌固深度会增大，设计时应考虑按不同工况分别计算嵌固深度进行包络设计。