电力负荷量及气象影响因素的极值模型分析
2022-03-01李妮妮徐付霞
李妮妮,徐付霞
(天津工业大学 数学科学学院,天津 300387)
电力负荷是指在发电厂中,各种电器装备在某一时刻所消耗的电力的总计,在现实工作中,电力负荷常常用电流所表示. 对用电量展开的预测工作将会对之后的发电规划和电能节约产生重要影响. 为了实现能源系统优化设计和科学决策,一个重要过程就是要提高电力负荷预测的准确度.
李军[1]采用了K-SVD-OMP的稀疏建模算法,实现了对电网负载在中短时段内变化的预测;魏腾飞[2]提出一种优化LSTM(长短期记忆)神经网络的方法,以此提升短期内预测电力负荷的准确性. 但是考虑到极端天气温度对电力负荷的影响,运用极值统计理论方法在电力负荷精准预测的研究中还很少见.事实上,发电设备中空调等与气象条件密切相关的用电设备对用电量的影响不断扩大,气象因素中温度、湿度、降雨量对负荷的影响更加突出,是提升负荷预测准确性的重要因素.
本文首先利用广义Pareto分布拟合某地区的电力负荷数据:对35 040个观测数据进行探索性分析,建立极值分布模型,利用极大似然法估计参数,再对模型进行诊断和分析.其次在影响用电负荷的气象因素中,选择日平均温度和日降雨量的365组数据,构造其二元超阈值模型,研究其极值相关性,是进一步研究气象因素对电力负荷影响的基础.
1 极值理论
极值统计主要研究很少发生,一旦发生却能产生重要影响的随机事件极端变异性的建模及统计分析方法. 广义极值分布(GEV)和广义Pareto分布(GPD或GP)是重要的极值分布模型,然后是二元超阈值模型.
1.1 GEV分布
Fisher-Tippett极值类型定理[3]:设随机变量X1,X2,…,Xn独立同分布,Mn=max(X1,X2,…,Xn),若存在常数列(an>0)和{bn},使得

(1)
成立. 那么H(x)必属于下列三种类型之一:
Ⅰ型分布(Gumbel分布):
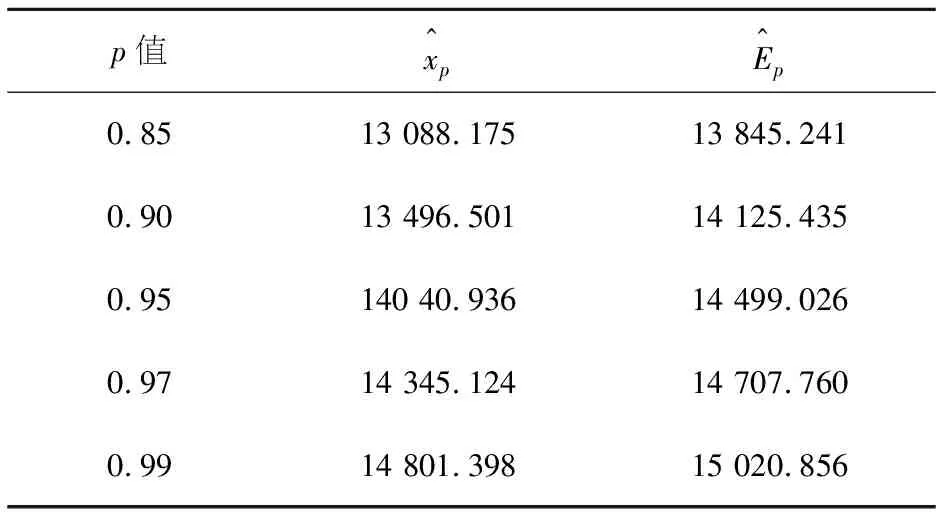
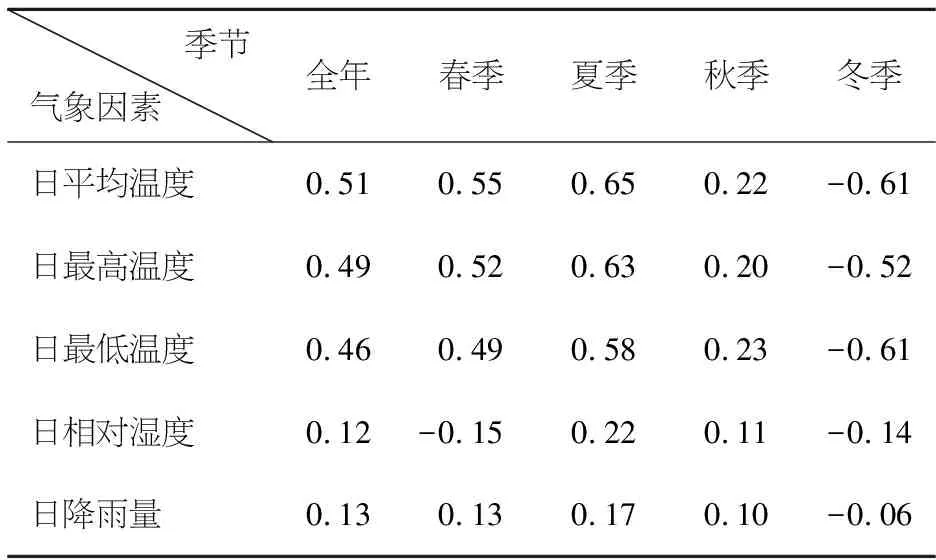
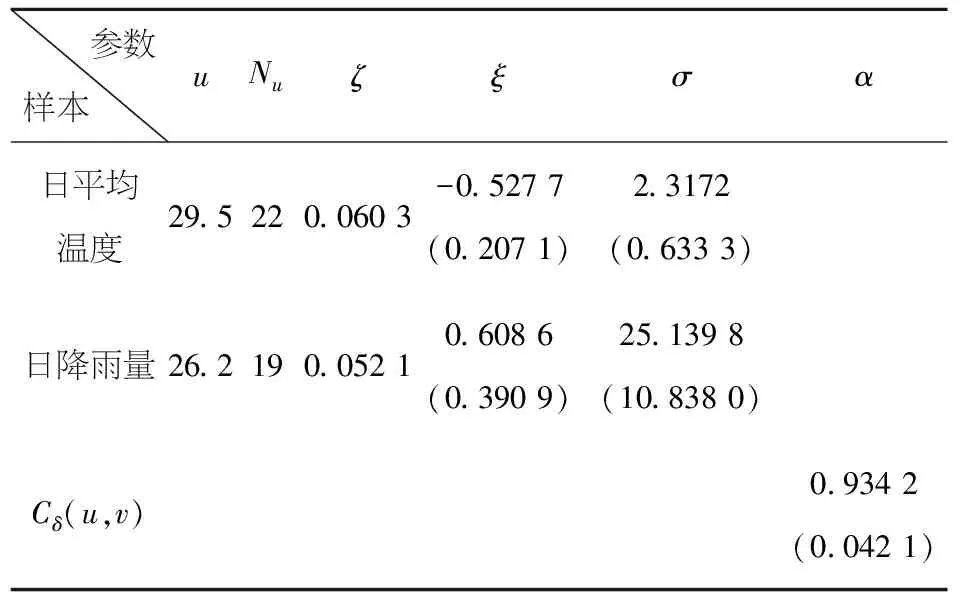
H1(x)=exp{-e-x},-∞ Ⅱ型分布(Fréchet分布): Ⅲ型分布(Weibull分布): 1+ξ(x-μ)/σ>0 (2) 其中:μ,ξ∈,σ>0.称H作广义极值分布,简称为GEV分布.当ξ>0时,是极值Ⅱ型分布;当ξ=0时,是极值Ⅰ型分布;当ξ<0时,对应于极值Ⅲ型分布[4]. GEV分布即区组分块最大值模型,须特别注意分块的个数. 这是由于在将数据划分为块时,一次只有一个最大值能被选择出来进行建模,但这将会导致大量浪费数据中原有的极值信息. 若选取一个较高的阈值,则超出该阈值的所有数据都将被视为极值,并且可以充分利用在极值数据中所容纳的信息. 广义Pareto分布是一种分布形式,可反映超出阈值的极端数据的统计特性. 设变量X1,X2,…,Xn独立同分布,分布函数是F(x),对于一个合适的阈值u,超出阈值的数记为Xi,则超出量Xi-u的分布函数是 由于F(x)未知,需要求出X-u的渐近分布.由Fisher-Tippett定理, (3) H(x;μ,σ,ξ)是GEV分布.选定合适的阈值u,当X>u时,X-u的近似分布就是广义Pareto分布,即 (4) 类似GEV分布,分别引入参数形状ξ,位置μ和尺度σ后,有 (5) 称X服从广义Pareto分布(GPD或GP分布),其中μ,ξ∈,σ>0. 设Nu为X1,X2,…,Xn内大于u的数量,Xi的分布函数尾部估计是[5] (6) (7) 平均超出量E(X|X>xp)的估计为 (8) 在将超出部分用广义Pareto分布拟合时,阈值的选取必须适当. 若数值太大,则超出数变少,模型参数估计值也会存在较大偏差;若数值太小,超出数分布存在偏差,估计量不是无偏的. 若用广义Pareto分布作为阈值u0超出量的近似分布. 则所有阈值u(u>u0),其超出数都遵循广义Pareto分布,且形状参数ξ一致,尺度参数[6] σu=σu0+ξ(u-u0). 于是有 因此,对于u>u0,E(X-u|X>u)是阈值u的线性函数. 对于超阈值观测值X1,…,Xn,用Nu说明超出数的数量.定义其平均超出量函数是 (9) 令X1,n=max{Xi,1≤i≤n},定义点集 {(u,en(u))∶u (10) 称为平均剩余寿命图.选适当阈值u0,令en(u)关于u≥u0近似为线性[7]. 关注图形中中点u0之后en(u)斜率的变化情况,若保持不变,则认为点u0是合适的阈值. (11) (12) 其中:ζx=Pr(X>u)=1-F1(ux),ζy=Pr(Y>u)=1-F2(uy). 对随机变量X,Y做变换: (13) (14) C(u,v;δ)=exp{-[(-logu)δ+(-logv)δ]1/δ} (15) 称为Gumbel Copula,参数δ≥1.当δ=1时,X,Y独立;若δ变大,则相关性b变强,当δ→∞时,X,Y完全正相关. 特别地,二元极值分布Logistic模型的尾部相关系数[9] (16) 若δ的值越大,则χ越大,也表示两个随机变量的极值相关性越强. 选取了天津市2019年1月1日~2019年12月31日的电力负荷数据,共35 040个用电量数据,单位是MW.表1给出了电力负荷数据的基本统计结果,其峰度系数小于0,偏度系数大于0,说明数据分布是右偏的,即有一条长尾在右,且分布较平缓,样本数据大多分布在均值周围,即电力负荷数据具有平缓右偏特征. 数据的直方图和折线图如图1,从图1中看出,此数据是右偏的,可用GP模型拟合数据的尾部分布[10].确定一个阈值,构造形如式(6)的近似的极值模型. 表1 电力负荷数据的基本统计量Table 1 Basic statistics of power load data 图1 电力负荷的直方图和折线图Figure 1 Histogram and line chart of electrical load 由R软件,得到由式(10)定义的平均寿命图,如图2所示. 图2 平均剩余寿命图Figure 2 Diagram of average remaining life 图3是不同阈值下参数和的估计值σ和ξ误差限.由阈值选取理论,确定此时的阈值为u=13 150.进一步,得到电力负荷数据中超阈值个数为Nu=1 966. 图3 尺度参数与形状参数估计图Figure 3 Scale parameter and shape parameter estimation diagram 由极大似然法得到参数σ和ξ的极大似然估计分别为1 075.00(17.153 0)和-0.457 3(0.009 8),括号里的数字是标准误,相应的对数似然函数值为37 358.7.由式(6),得到超过阈值的电力负荷的尾部分布为: (17) 图4是模型诊断图.其中P-P图的点呈单位对角趋势;Q-Q图的点基本分布在一条直线上;由参数ξ<0,此时重现水平图应是凸曲线,即说明模型是恰当的;密度分布图与折线图也显示出一致的趋势.检验结果表明,用Pareto模型式(17)分析电力负荷数据的超出数比较合理. 图4 模型诊断图Figure 4 Model diagnostic diagram 表2 重现水平和超阈值的平均用电负荷估计Table 2 Average power load estimates for recurrence levels and over thresholds 由表2,当p=0.90时,得到用电量的估计值为13 496.501,即所有用电量中,存在10%的用电量超过该数值. 按照每天24 h分析,大约一天有2.4 h的用电量超过该数值,这个结果合乎我们实际的统计数据. 发电公司若依照此数值来设计发电方案,那么可实现社会人人用电的概率为90%. 通过充分利用数据中的极值信息,构造电力负荷数据的一元极值模型. 使发电公司在保证人人用电同时,尽可能减少发电设备和发电量,节约资源[11]. 采用季节划分:春季3~5月,夏季6~8月,秋季9~11月,冬季12~次年2月[12].图5是天津市2019年1月1日~2019年12月31日的日平均用电负荷曲线图,可见春季和秋季平均用电负荷量相近,而夏季和冬季的用电负荷量明显多于春秋两季,这与当地气候有关,在夏季和冬季,空调和暖气使得用电负荷量成为全年的两个峰值. 图5 全年日平均用电负荷曲线Figure 5 Annual average daily power load curve 本文统计了天津市2019年全年的五个气象指标:日平均、最高、最低温度,相对湿度和降雨量,共365组数据,将日均用电负荷与这些要素做相关分析,全年及各季节相关系数见表3. 通过表3看出,在分别按全年统计和按一年分春夏秋冬四季统计的分析中,在温度、相对湿度、降雨量这三个影响因素中,对用电负荷量产生最多影响的是温度. 冬季用电量均与日平均、日最高、日最低温度呈现一致的负相关,平均相关系数达到0.5以上.夏季温度与用电负荷存在显然的正相关,平均相关系数达到0.6以上. 且在平均、最高、最低温度这三个要素中,与用电负荷量具有最强相关性的是平均温度. 表3 日均用电负荷与全年及各季日气象要素相关系数Table 3 Correlation coefficient between average daily power load and annual and seasonal daily meteorological elements 上述五个气象指标中,与日平均温度相关性较强的日最高、最低温度,适合用线性模型描述它们间的相关性.下面以日平均温度和日降雨量为例,研究两者的非线性极值相关性. 日平均温度和降雨量数据的基本统计描述见表4,可见日平均温度数据偏度小于0,峰度小于3,数据的分布是左偏的,且分布平缓;日降雨量数据的偏度大于0,峰度远大于3,具备尖峰右偏特点. 表4 日平均温度和日降雨量的基本统计量Table 4 Basic statistics of daily mean temperature and daily rainfall 经过计算,日平均温度和日降雨量之间的线性相关系数r=0.149 892 6,秩相关系数Kendallτ=0.223 595 5,Spearmanρ=0.287 724 1,尾部相关性度量χ为0.155 207 3.图6是日平均温度和日降雨量数据的散点图,可以用看出这两个因素的变化情况大致趋于一致. 图6 日平均温度和日降雨量散点图Figure 6 Scatter plot of daily mean temperature and daily rainfall 接下来,对原始数据(xi,yi),i=1,2,…,365,作变换 图7 经过变换边缘分布为均匀分布的的散点图Figure 7 A scatter plot whose edges are transformed to be uniformly distributed 图8 二元超阈值模型的散点图Figure 8 Scatter plot of binary superthreshold model 表5 模型的参数估计结果Table 5 Parameter estimation results of the model 由式(11)~(15),得到日平均温度和日降雨量的尾部分布函数分别为: (18) (19) 尾部联合分布函数为: 通过计算可预测日平均温度和日降雨量数值的未来走向[16]. 例日平均温度数值大于30和日降雨量数值大于28的概率分别是: Pr(X>30)=0.047 951, Pr(Y>28)=0.048 574. 当日平均温度数值超过30时,日降雨量数值超过28的概率为 Pr(Y>28|X>30)=0.726 137. 当日降雨量数值超过28时,日平均温度数值超过30的概率为 Pr(X>30|Y>28)=0.716 824. 可见,两个事件各自出现的概率很小,不超过0.05,但当其中一个事件出现时,另一个事件也出现的概率却很大,超过0.7,这表明日平均温度与日降雨量有较强的尾部相关性. 本文分别构造了一元和二元极值模型,探究了它们在用电负荷预测和极值相关性研究中的应用.先建立用电负荷的广义Pareto分布模型,得到以90%的概率实现人人用电时的平均用电量.由此可以了解用电量的情况,理性应对超额用电和用电过剩. 将极值统计和Copula理论结合,建立二元超阈值模型,应用在日平均温度和日降雨量两个影响因素的极值相关性分析中,得到日平均温度和日降雨量的尾部联合分布函数. 可以对两个指数的未来走向进行较精确的预测分析.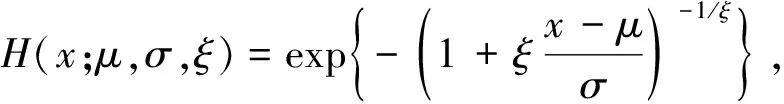
1.2 广义Pareto分布


1.3 二元超阈值模型

2 电力负荷数据的一元极值分析
2.1 数据分析


2.2 参数估计


2.3 模型诊断

2.4 结果分析


3 日平均温度和日降雨量的二元极值分析
3.1 气象影响因素分析

3.2 日平均温度和日降雨量的极值相关性


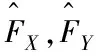

3.3 二元超阈值模型


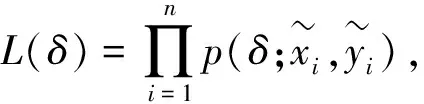
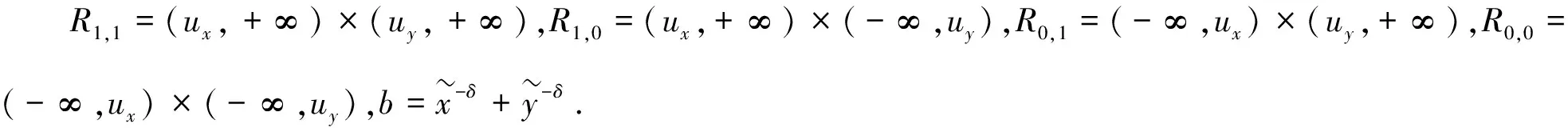
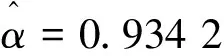

4 结 语
