高速公路合流区可变限速和换道协同控制研究
2022-03-01李巧茹王少航
李巧茹,王少航,陈 亮
(河北工业大学 土木与交通学院,天津 300401)
0 引 言
交通需求增加导致高速公路合流区通行能力下降,拥堵问题频发。通过智能交通技术来提高现有公路基础设施效率,成为智能交通控制领域研究的热点。
可变限速(VSL)控制是最常用的控制策略之一。VSL通过调整交通瓶颈上游的速度限制,可以提高交通流的机动性[1]、安全性,并减少污染和降低能耗。J.R.D.FERJO等[2]基于模型预测控制(MPC)设计了可变限速控制策略;G.R.IORDANIDOU等[3]将局部反馈MTFC应用于交通瓶颈可变限速研究;C.RONCOLI等[4]研究发现,接近瓶颈处车辆的强制换道行为可能导致这些VSL方法效果不理想;Y.ZHANG等[5]指出,现有的大多数VSL方法在微观仿真中对交通流动性的改进不大,并首次提出结合VSL和换道(LC)控制的协同控制方法。
在某些情况下,VSL控制产生的限速值可能很小,甚至小于20 km/h,与高速公路实际限速要求相悖。C.B.ZHANG等[6]通过优化车辆在车道上的分布,减轻了车道变化路段强制换道的负面影响;田丽萍等[7]针对高速公路合流区,提出一种主线段车辆动态限速方法,通过主线车辆减速来避免车辆合流时的冲突;E.YE等[8]提出了一种二级交通控制方法,优化合流区上游车道的车辆密度,并建议冲突车辆提前变道。然而,当交通需求较高时,仅采用LC控制不足以减少交通拥堵。Y.ZHANG等[9]结合VSL和LC控制,为交通事故点上游的车辆提供换道建议;Y.GUO等[10]提出了一种智能网联车辆(CAVs)环境下集成的VSL和LC的控制方法,考虑VSL和LC相互作用,以最大限度提高交通效率;陈亮等[11]设计了一种基于多分类支持向量机的车辆换道识别模型,为微观交通仿真提供了技术支持;T.L.PAN等[12]提出了一种新的中观多车道CTM模型,能够同时模拟强制和任意改变车道的行为,并可用于预测交通事件发生或车道控制策略的仿真。
综上,将VSL和LC相结合的协调控制研究较少,尤其是在LC控制中未考虑由LC控制本身对交通流的干扰。笔者将换道控制造成的容量下降引入LC控制中,减少车辆自主变道对主线交通流的干扰,并与VSL结合,以期提高控制系统对不同交通需求的适应性。
1 公路瓶颈模型
交通瓶颈是指通行能力最低的点,由于交通瓶颈的存在,随着交通需求的增加,会出现车辆排队现象。车道数变少、交通事故发生、合流区的车辆汇入或其他道路状况都可能导致交通瓶颈,交通瓶颈的流量决定了整个公路路段的通行能力。因此,瓶颈处交通流的建模对于设计有效的交通控制策略至关重要。
图1为高速公路合流区瓶颈示意,由一条3车道的高速公路主线路段和单车道的入口匝道组成。设高速公路主线的通行能力为C,匝道车辆能全部顺利汇入高速公路主线段。当匝道上的交通需求为0时,瓶颈处的理想通行能力Cb=C;当匝道上的交通需求为qr=ρrvr时,从匝道汇入主线的车辆将在加速车道路段对主线车流形成交通障碍,此时瓶颈处的理想通行能力Cb=C-qr。根据三角形基本图假设,瓶颈上游密度ρd较低时,瓶颈上游理想流量qb=vfρd,其中vf为高速公路主线自由流速度;而当瓶颈上游密度ρd大于临界密度ρdc,即瓶颈的需求大于其容量Cb时,停滞的车辆将在瓶颈上形成车队,并向上游传播。车队中的车辆强行改变车道会降低其他车道上车流速度,降低瓶颈容量[13]。瓶颈路段流量-密度关系如图2,图中q为流量,ρ为密度。当队列形成时,容量将下降到C′b=(1-ε)Cb,且ε∈(0,1),ρd与qb的关系如下:
(1)
Cb=vfρd
(2)

图1 高速公路合流区瓶颈示意Fig. 1 Schematic diagram of bottleneck in expressway confluence area

图2 瓶颈路段流量-密度关系Fig. 2 Flow-density relationship of bottleneck section
2 基于元胞传输模型的可变限速研究
2.1 元胞传输模型
元胞传输模型将高速公路主线段分成N段,分别用qi、ρi、vi、Li来表示元胞i={1,2,…,N}的流量、密度、平均车速和路段长度,并在每个时间间隔t对各个元胞的交通状态参数更新。经典的CTM模型(图3)中Qc为路段通行能力,vf为自由流速度,ρc为关键密度,w为交通波传播速度,ρj为堵塞密度,vvsl为可变限速值,Q′c、ρ′c分别为可变限速下的路段通行能力和关键密度。
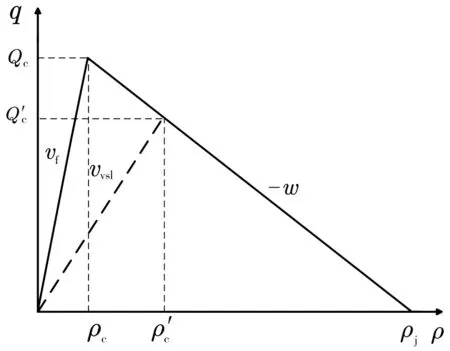
图3 可变限速路段流量-密度关系(CTM模型)Fig. 3 Flow density relationship of variable speed limit section (CTM modle)
t时刻元胞的流量和速度如式(3)、式(4):
qi(t)=min{vi-1(t)ρi-1(t),Qc,[ρj-ρi(t)]w}
(3)
(4)
由此可得元胞t+1时刻密度为:
ρi(t+1)=ρi(t)+[qi-1(t)-qi(t)]/Li
(5)
2.2 限速下的元胞传输模型改进
可变限速下元胞传输模型如图3中斜率为vvsl的虚线,此时车辆的最大速度由自由流速度vf变为限速值vvsl,可变限速下的通行能力Q′c和对应的关键密度ρ′c为:
Q′c=vvslwρj/(vvsl+w)
(6)
ρ′c=Q′c/vvsl
(7)
当元胞密度小于等于关键密度时,车辆不再以自由流速度行驶,而是以限速值vvsl行驶;当元胞密度大于关键密度时,车辆期望速度小于限速值,车辆将以期望速度行驶,即:
(8)
元胞i的流量为:
qi(t)=min{ρi-1(t)vi-1(t),Q′c,[ρj-ρi(t)]w}
(9)
元胞密度是由上一时刻的元胞密度和元胞流量决定的,不受限速值的影响,故元胞密度表达式与式(5)一致。
3 可变限速与换道协同控制
3.1 换道协同控制
换道协同控制应用于合流区上游,如图4。换道控制的目的是降低高速公路右侧车道的车流密度,通过控制使主线车辆提前变道,以便入口匝道车辆能够顺利汇入高速公路主线。在保证交通顺畅的情况下,通过使合流区上游的车辆变道,减少靠近合流位置的车辆数,最大限度减少车辆汇入干扰,降低交通流的恶化程度,减少容量下降的影响。图中,vi,vsl、qi、ρi、Li分别为元胞i={1,…,N}的限速值、流量、密度以及路段长度,qb为从主线汇入合流区的流量,ρr为匝道车流密度。

图4 协同控制示意Fig. 4 Schematic diagram of collaborative control
换道控制通过最小化目标函数确定每条车道上的最优车辆数,并在每个时间间隔向智能网联车辆(CAVs)提供换道建议,以实现最优车流密度分布。换道控制的目标为采用较小的变更车道次数实现每条车道的最佳车辆密度。由于控制是通过给车辆提供变道建议来实现,采用控制路段的车辆数来代替交通密度,代替后的最优车流密度的目标函数如式(10):
(10)
(11)

理想车道车辆数的表达式如式(12):
(12)
式中:γ为匝道干扰系数,γ越小换道区最右车道的车辆数越小,匝道车流汇入就越顺利;ρc是由CTM基本图得出的临界密度;ρrp为匝道的预测密度;L为换道控制路段长度,即LN=L。
换道控制模型中假定车辆在换道区只向左进行换道,且换道前、后的车辆数守恒,据此作出如下约束条件:
(13)
(14)

(15)
式中:W为换道区随机车道编号,W∈[1,l]。
式(13)~式(15)分别保证了车辆数守恒、向左换道规则以及控制车辆数为整数的原则。
车辆换道会对上游交通产生干扰,造成交通拥堵和道路容量下降[14-15]。为了达到最佳的车流密度,需要大量车辆在换道区进行换道,但过多的换道行为或过度控制都会导致系统恶化,造成交通震荡,影响交通安全。在保证换道不会导致上游交通流恶化的前提下,要维持一定流量,存在一个车道变化的最大数量,其对应的单位长度最大换道率与主线段的平均车道流量的关系如下:
(16)

(17)
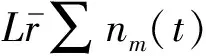
3.2 换道控制的影响
为了研究3.1节提出的合流区变道控制效果,采用MATLAB建立CTM模型,构建一个长为8.4 km的3车道高速公路路段,如图1。设匝道需求为1 500 veh/h,在未使用VSL的前提下,利用中观CTM模型研究不同交通需求水平下,瓶颈上游流量qb与瓶颈上游换道区密度ρd间的关系。

图5 LC控制路段流量-密度关系Fig. 5 Flow density relationship of LC control section
由图5可知:采用LC控制时,瓶颈的容量Cb≈4 160 veh/h,对应的关键密度ρdc=14.75;当无LC控制时,qb在达到关键密度ρdc前就达到了最高值(约为2 400 veh/h)。在无换道控制下,瓶颈上游车辆由于在接近瓶颈前未能提前换道,故在瓶颈处被迫强制换道并造成瓶颈附近车辆大幅减速,最终导致主线容量下降。说明LC控制能够减少瓶颈处排队长度,并降低车流密度,使系统具有连续性。
由LC控制下流量-密度关系可知,当上游交通需求小于等于瓶颈容量时,换道区以及合流区车辆以自由流速度vf通过瓶颈;反之,换道区以及合流区由于密度过大造成车辆平均速度降低,最终导致瓶颈截面流量下降,换道控制下的瓶颈流量和密度关系如式(18):
(18)
式中:qb为换道区流入合流区的流量;wd为换道区瓶颈交通波传播速度;ρdj为换道区瓶颈堵塞密度。
3.3 可变限速值的确定
虽然换道控制能够避免高速公路主线容量下降,恢复CTM模型的连续性,但当需求大于瓶颈容量Cb时,合流区仍会出现拥堵。所以还需要在换道区上游设计一个VSL控制器来稳定上游交通流。均匀化所有截面密度,使它们收敛到一个对应瓶颈最大流量的临界密度ρe。
当上游交通需求小于等于瓶颈容量时,限速值为自由流速度vf。反之,为了控制进入可变限速路段的车流量,需要降低可变限速路段的限速值,依据可变限速控制的期望密度ρe和图5中的流量-密度关系,可变限速控制路段1的期望限速值和期望密度应满足:
(19)

可变限速控制路段1的期望限速值和期望密度可由公式(19)得出:
(20)

3.4 基于模型预测控制(MPC)的可变限速控制
传统的PID控制模型因其结构简单、易于实现而被广泛应用,但是由于模型采用当前状态进行反馈,所以对交通流的控制存在一定的滞后。MPC通过当前交通流参数预测未来交通状态,避免了控制滞后,达到短时间间隔最优控制效果,笔者在MPC的框架下提出可变限速控制系统如图6。
基于MPC的可变限速系统,以改进的CTM模型作为预测模型,并通过检验换道区的实测交通密度ρd与期望密度ρdc的偏差,对基于模型的预测限速值进行反馈修正。可变限速的修正值如式(21):
u1(k)=KI[ρd(k-1)-ρdc(k-1)]
(21)
式中:u1(k)为第k限速周期内的对可变限速路段1的限速修正值;KI为限速修正值的反馈系数。

图6 基于MPC的可变限速控制模型Fig. 6 Variable speed limit control based on MPC
3.5 可变限速控制的约束
由于车辆难以适应过大的限速变化幅度,而且为了交通安全和道路使用者的体验,速度限制不能过高或过低,故对可变限速值采用以下限制:
1)控制周期。可变限速控制应采用离散的控制周期Tk,且控制周期Tk应为数据采集周期Tc的整倍数。
2)可变限速值的选取。考虑驾驶员的可操控性,可变限速值一般选取5 km/h的整倍数,且最大限速值不得超过自由流速度vf,最小值不得小于静态限速的最小值,一般取40 km/h。
3)限速变化幅度。为安全考虑,可变限速值在空间和时间上的变化幅度都不宜过大,限速变化幅度一般取5 km/h的整倍数,分别选取10、20 km/h作为可变限速在不同时间同一路段以及同一时间不同路段的最大变化幅度。
4 仿真与分析
4.1 仿真场景与参数设置
为测试和评估协同控制系统性能,利用宏观和中观CTM模型在MATLAB中分别对无控制、VSL控制以及笔者提出的协同控制进行仿真。使用宏观模型来评估笔者提出的协同控制中VSL控制器的性能,由于宏观模型未考虑车道变换的影响,因此将LC控制模型应用到相应的中观模型中,利用中观模型数据对宏观元胞传输模型进行对接校正,并假定车辆对协同控制的服从率为100%。
仿真场景如图7,合流区上游是一条3车道的路段,主线段中每个路段的长度为600 m,静态限速为95 km/h,容量为5 700 veh/h;匝道长度与加速车道长度均为200 m,静态限速为60 km/h,容量为1 500 veh/h。

图7 仿真路段与场景设置Fig. 7 Simulation section and scenarios setting
仿真中的单车道交通需求曲线如图8,入口匝道上的峰值流量为1 000 veh/h,主车道上的峰值流量为5 000 veh/h,仿真时间为120 min,峰值时间为20 min。限速路段的设置长度若过长,则无法实现对瓶颈区域交通的有效限制;若距离过短,则一旦瓶颈区域排队上溯将导致限速控制失效。因此,参考文献[11]取限速路段长度为500~600 m。

图8 交通需求设置Fig. 8 Traffic demand setting
限速标志设置在路段9、10、11的起始点,交通流在限速段被限流,并将流量控制在瓶颈容量附近。路段12为速度释放段,作用是使车辆从限速状态下的高密度,恢复到自由流状态下的低密度。路段13为换道控制段,通过给CAVs车辆提供变道建议,调整主线段车流密度,为入口匝道的车流汇入提供良好的环境。
模型及仿真参数设置如表1,表中α1、α2、α3、β为换道控制目标函数的加权系数,α1、α2、α3的数值依次变小,代表越靠近右侧的车道受到匝道车辆汇入的影响越大;β的设置考虑了瓶颈流量与换道总次数的综合影响;Kc为可变限速控制周期内限速值向期望密度调整的速率。

表1 模型及仿真参数Table 1 Model and simulation parameters
4.2 仿真结果分析
由瓶颈理论可知,当换道区密度为期望密度ρdc时,合流区流量达到最大值,此时合流区密度接近关键密度20 veh/km。可变限速的目的就是在交通需求过大时限制瓶颈上游的容量,将换道区密度维持在期望密度附近,达到合流区流量最大化,瓶颈容量与换道区流量差为容量下降值,容量下降值越小道路利用率越高。
图9~图11分别为无控制、VSL控制、协同控制下交通状态变化情况。

图9 无控制下交通状态Fig. 9 Traffic state without control

图10 VSL控制下交通状态Fig. 10 Traffic state under variable speed limit control

图11 协同控制下交通状态Fig. 11 Traffic state under cooperative control
由图9可知:无控制下的换道区密度随着交通需求的增加而迅速增加,其峰值远远超过了换道区的理想密度,并且在50 min交通需求下降后换道区密度仍保持峰值不变,直到80 min换道区密度才迅速下降;换道区流量在交通需求高峰时段明显低于瓶颈容量,其差值即为合流区瓶颈的容量下降值。
由图10可知:换道区密度随着交通需求的增加而迅速增加,其峰值高于换道区的理想密度且明显低于无控制下的换道区密度峰值,在50 min交通需求下降后换道区密度随着时间呈阶梯式下降;VSL控制下换道区流量在交通需求高峰时段也明显高于无控制下的换道区流量,合流区瓶颈的容量下降减少。
由图11可知:换道区密度随着交通需求的增加而增加,在交通需求高峰时段,换道区密度稳定在换道区的理想密度附近,换道区流量也稳定在合流区瓶颈容量的附近。与其他控制方案相比,协同控制下的换道区密度与合流区瓶颈容量下降数值明显变小。从换道区和合流区交通状态变化情况可以看出,协同控制下的交通流在交通需求高峰时段后能更快地恢复到自由流状态。
图12为3种控制方案下换道区密度和合流区流量变化情况。由图12可知:协同控制下的换道区密度一直低于其他两种控制方案,且20~80 min时段内,VSL控制和无控制下的换道区密度均出现骤增和骤降现象,而协同控制下的换道区密度变化较为平缓,无控制、VSL控制以及协同控制下的换道区密度的波动范围分别为11~53、11~32、11~20 veh/km。协同控制下的合流区流量一直高于其他两种控制方案,且在交通高峰时段内,瓶颈区域通行交通量维持较高状态,无控制、VSL控制以及协同控制下的合流区流量分别维持在4 423~5 464、4 791~5 611、5 292~5 685 veh/h。由此可知,相较其他两种控制方案,协同控制能有效提升瓶颈区域的安全性能和通行效率。
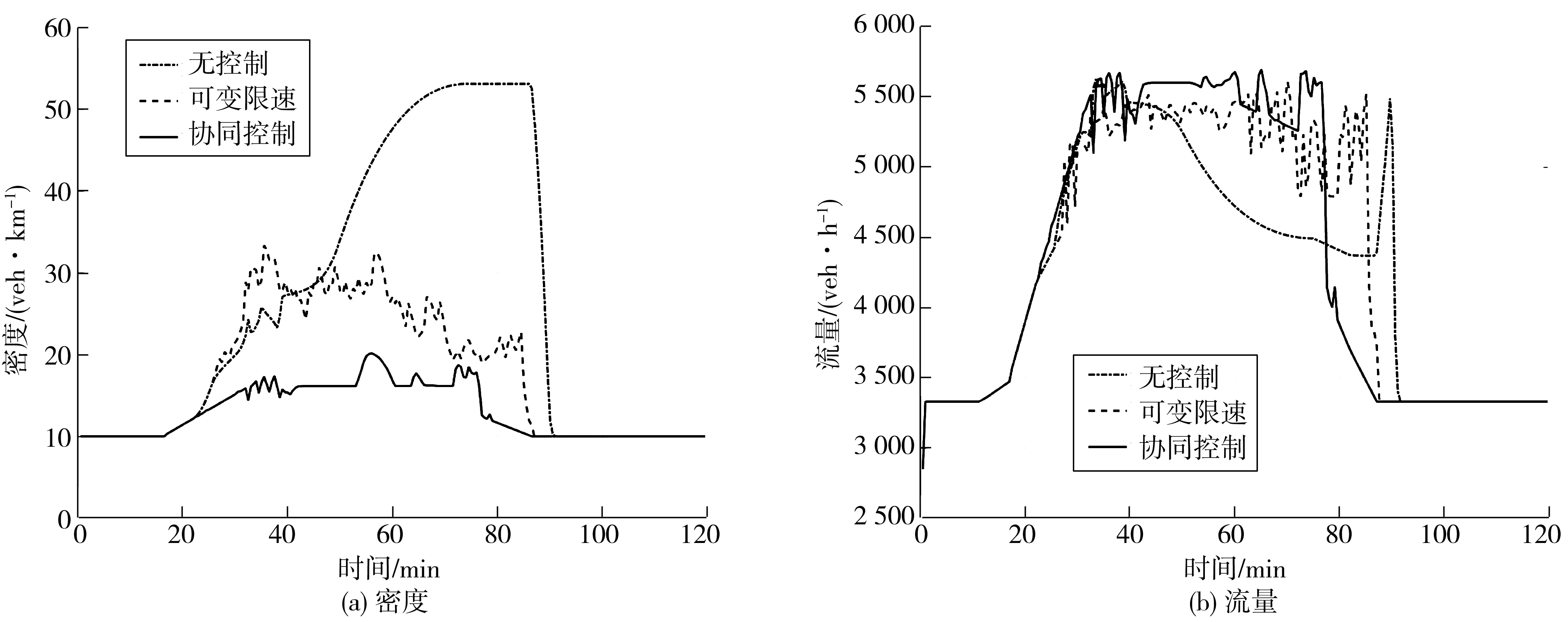
图12 3种方案下控制效果对比Fig. 12 Comparison of control effects of three kinds of schemes
为进一步说明协同控制的性能,采用瓶颈处的平均流量和平均旅行时间两个指标来说明。仿真发现,主线交通需求增长在17 min时开始影响合流区,为了数据精确,在仿真中选取测量时间为17~80 min,测量路段为路段13~路段14。
设测量时间通过瓶颈的车辆数为N(t),每车道密度为ρm,则平均旅行时间Tavg和平均流量Qavg的定义为:
(22)
不同策略下的平均旅行时间Tavg和平均流量Qt如表2。

表2 协同控制评价指标Table 2 Evaluation index of collaborative control
由表2可知:协同控制在旅行时间和平均流量这两个评价指标上都明显优于其他方案。与无控制方案和VSL控制方案相比,协同控制的平均旅行时间分别降低了58.55%、35.68%;平均流量分别提高了9.09%、2.35%。综上,提出的协同控制在通行效率、交通安全方面均有明显改善。
5 结 语
基于CTM模型设计了高速公路合流区可变限速和换道协同控制策略,在提出的协同控制策略中,LC控制通过预测瓶颈容量和交通需求为联网车辆CAVs提供变道建议,缓解瓶颈处通行能力下降的现象,并利用基于MPC框架的VSL调控瓶颈上游流量,使上游车流密度收敛到期望密度下的平衡状态,从而实现瓶颈处的流量最大化。为验证所提出的协同控制策略的性能,利用改进的CTM模型在MATLAB软件中进行仿真,并采用对比分析的方法对协同控制策略的性能进行分析和评价。仿真结果表明:提出的协同控制策略能有效缓解合流区瓶颈在车流高峰期的容量下降现象,提高合流区瓶颈的通行能力;与无控制方案和VSL控制方案相比,协同控制的平均旅行时间分别降低了58.55%、35.68%;平均流量分别提高了9.09%、2.35%。
