基于聚类和局部线性回归的初至波自动拾取算法

高 磊，罗关凤，刘 荡，闵 帆，2*

（1.西南石油大学计算机科学学院，成都 610500；2.西南石油大学人工智能研究所，成都 610500）

0 引言

在地震数据处理过程中，确定初至波的到达时间是非常重要的，它将直接影响后续步骤的精度，例如，动校正［1］、静校正［2］和速度分析［3］等。除此之外，错误的初至波拾取结果也会对后续子波的分析造成干扰，使专家不能正确地进行事件识别、震源反演，以及震源判断等。然而，在强烈的背景噪声和复杂近地表条件地干扰下，现有算法的准确率会降低，如何准确地拾取初至波是本领域目前亟待解决的问题。

早期的初至波拾取由专家根据经验手动完成，这种方式过分依赖于专家经验，耗时且主观［4］。后来发展为半自动拾取，由专家先拾取一部分初至波，然后通过软件确定剩下的初至波，这种方式虽然在一定程度上提升了效率，但仍不能满足实际需求。随着自动化拾取算法开始兴起，出现了能量比法、相关法、聚类法等各种初至波自动拾取算法，其中聚类法是目前较为流行的初至波拾取算法。本文通过分析各种聚类算法的优缺点，选取了k均值（k-means）聚类和基于密度的噪声应用空间聚类（Density-Based Spatial Clustering of Applications with Noise，DBSCAN）这两种算法来拾取初至波。

由于DBSCAN 对噪声不敏感，聚类效果好，但对于庞大的地震数据，它的时间复杂度高；而k-means 对噪声比较敏感，但其时间复杂度低。因此，本文提出将这两种聚类相结合，先用k-means 技术找到初至波簇；再用DBSCAN 技术在初至波簇中拾取初始初至波。这种方式充分利用了两种聚类算法的优点，DBSCAN 不直接在整炮数据上运行，而是在初至波簇中进行拾取，这种方式可以提高运行速度，准确率也得到了很大的提升。

本文将DBSCAN 用于初至波拾取，取得了较好的效果，主要工作包括以下几个方面：

1）基于k-means 技术选取初至波簇；

2）基于DBSCAN 技术在初至波簇中拾取初始初至波；

3）通过局部线性回归来补齐初始初至波中的缺失值；

4）通过能量比值对初始初至波中的错误值进行调整。

1 相关工作

初至波拾取在地震勘探领域中发挥着非常重要的作用，是地震数据分析的预处理阶段，被广泛地应用到各领域中，具有重要的研究意义。接下来本文将对初至波拾取的发展历程进行一个简单的介绍。

目前，国内外学者进行了很多研究，提出了多种初至波拾取方法，本文主要从三个方面进行介绍：

1）以单道为基础的能量比法，主要以Coppens 算法［5］及其变体为代表。Coppens 使用两个窗口内的能量比来处理数据；Sabbione 和Velis［6］改进了Coppens 算法，以熵和分形维数算法来拾取初至波；在此基础上，Allen［7］利用短期平均值与长期平均值之比（Short-Term Average/Long-Term Average，STA/LTA）来提高准确率；Lee 等［8］用多个窗口代替了传统的两个窗口以获得更可靠的结果。

2）以多道为基础的互相关法。Peraldi 等［9］考虑了相邻道之间的能量，提出了互相关算法；Senkaya 等［10］进一步考虑了每一道数据和源小波之间的互相关；Molyneux 等［11］提出使用最大互相关值作为评价准则的直接相关算法来拾取初至波。

3）以整个数据集为基础的聚类算法。Zhu 等［12］提出了一种基于聚类的初至波拾取算法；周竹生等［13］提出了基于加权k均值聚类的多属性初至拾取算法；Gao 等［14］将滑动窗口与模糊c均值聚类结合，采用滑动窗口获得范围带，模糊c均值只需在范围带里面检测初至波，可以获得更加精确的效果。

这些算法在高质量数据集中能够取得较好的效果，但在信噪比（Signal-to-Noise Ratio，SNR）较低的数据集中，都有一定的缺陷。例如以单道为基础的算法未考虑初至波之间的关系，拾取精度不稳定［15］；以多道为基础的互相关法在相关性较弱的地震数据中，准确率有所下降；以整个数据集为基础的大多数聚类算法易受到噪声干扰，聚类效果差，但这种算法考虑了整个数据的分布，并且可以根据初至波的特性将其最大限度地划分为一簇。因此，本文将继续沿用基于聚类的初至波拾取方法，提出了基于聚类和局部线性回归的初至波自动拾取算法（First-arrival automatic Picking algorithm based on Clustering and Local linear regression，FPCL），取得了较好的效果。

2 问题及定义

在本章中，将建立一个数据模型，并介绍初至波拾取问题及其相关定义。

2.1 数据模型

在地震勘探中，野外数据的采集主要是通过炮点激发，并由不同的检波器接收。其中，每个检波器接收到的波形记录对应一道地震数据，所有地震道的数据集合组成了共炮点道集。本文采用共炮点道集作为数据集来进行初至波拾取。

图1 是输入的原始数据和拾取结果。它表示一个包含了210 道数据，每道数据含有700 个样本点的共炮点道集，水平坐标表示地震道的数量，垂直坐标表示每道的样本数量。对于每一道数据，都能找到一个位于波峰的初至波，其中，白点是每道的初至波位置。

图1 共炮点道集和初至波Fig.1 Common shot gather and first-arrivals

2.2 初至波拾取问题及其相关定义

在地震勘探中，由炮点激发并最先到达检波器的地震波称为初至波［16］。初至波拾取是地震数据分析的重要预处理阶段，它可以定义如下：

问题1 初至波拾取问题。

输入 共炮点道集A=[aij]是一个m×n的矩阵，n是地震道数，m是每道的样本数，aij是第j道的第i个样本能量值。

输出 初至波位置数组F=[f1，f2，…，fn]，fj为第j道的初至波位置。

定义1初至波簇是一个l×3 的矩阵D=[di′j′]，其中，l=|Sk*|代表初至波簇的样本点个数，di′1=aij，(i，j)∈Sk*代表能量值，di′2存储行下标i，di′3存储列下标j。

定义2分割线Zk=，其中Zk代表第k簇的分割线，

3 本文算法

FPCL 算法由预拾取和微调两个阶段来实现。预拾取阶段通过k-means 和DBSCAN 技术来找到初始初至波。由于DBSCAN 具有传递性且抗噪能力强，适合用于拾取初至波，但它直接在整炮数据上运行时间复杂度较高，因此，本文利用k-means 时间复杂度低的优势，先在整炮数据上采用k-means 技术找到初至波簇，再采用DBSCAN 技术在初至波簇中拾取初始初至波，这样的方式可以提高抗噪能力和运行速度。微调阶段通过局部线性回归和能量比值最小化技术调整初始初至波以提高准确率。通常来说，初至波具有相关性强、能量强的特点［13］。根据相邻道初至波之间相关性强的特点，使用局部线性回归来补齐初始初至波中的缺失道；根据初至波能量强的特点，使用能量比值最小化技术来调整错误值。

3.1 预拾取阶段

本节详细描述了基于k-means 和DBSCAN 技术的初至波预拾取过程。k-means 技术用于选择初至波簇，DBSCAN 技术用于从簇中拾取初始初至波。

3.1.1 基于k-means选择初至波簇

由于k-means 算法的时间复杂度接近于线性，它被用来选择初至波所在的簇。对于给定的样本集A=[aij]，按照样本之间的距离大小将样本集划分为e1个簇。该算法的目标是迭代更新聚类中心ck以最小化平方误差E：

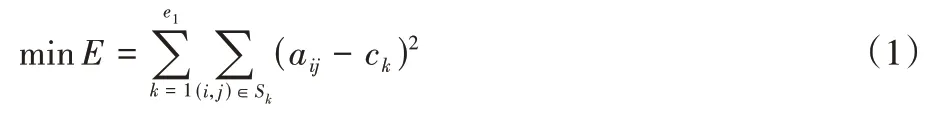
其中：e1是聚类中心个数；aij是第j道的第i个样本能量值；ck是第k个聚类中心。ck通过如式（2）进行迭代更新：

其中：t表示当前迭代次数；表示迭代更新后的第k个簇的中心；表示当前迭代时属于第k个簇的样本索引集合。的计算公式为：

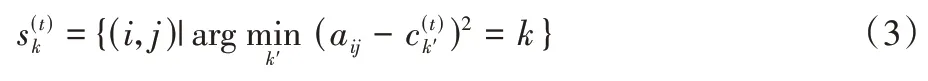
k-means 聚类结束后，选择平均能量值最大的簇作为初至波簇，目标函数设计如下：

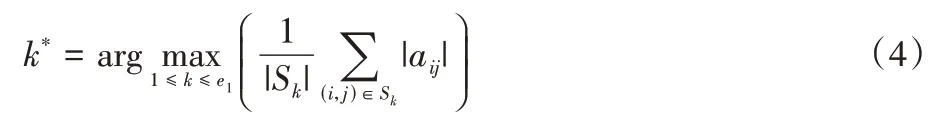
其中：Sk表示迭代终止后属于第k个簇的样本索引集合。

算法1 描述了基于k-means 选取初至波簇的过程。第1）行将输入得数据集归一化到［-1，1］；第2）行根据式（1）～（3）执行k-means 聚类；第3）行根据式（4）选择平均能量值最大的簇；第4）行根据定义1 初始化含有三个属性（能量值、行索引和列索引）的初至波簇D；第5）行返回初至波簇D。

3.1.2 基于DBSCAN拾取初始初至波

首先，将初至波簇D中的样本点依次按照下列公式标记为核心点、边界点或噪声点：

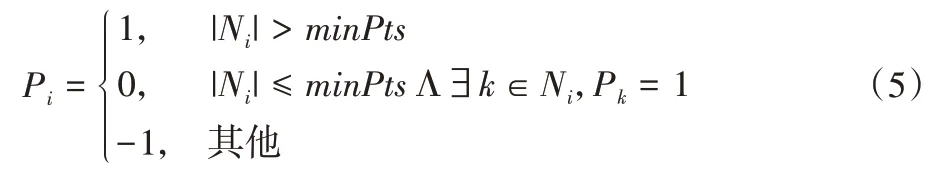
其中：Pi表示第i个点的类别，“1”表示核心点，“0”表示边界点，“-1”表示噪声点；minPts表示邻域内的最小点个数；Ni表示第i个点的邻域。Ni的计算公式为：

其中：Eps表示邻域半径。

然后，循环遍历所有的核心点，连通与该核心点距离小于半径Eps的所有核心点与边界点，并形成一个簇。

DBSCAN 聚类后，数据被分成e2个簇，对于每个簇，从每道中提取出第一个属于该簇的样本点并形成一条分割线，因此可以得到e2条分割线。

最后，选择最完整的一条分割线作为初始初至波。目标函数设计如下：

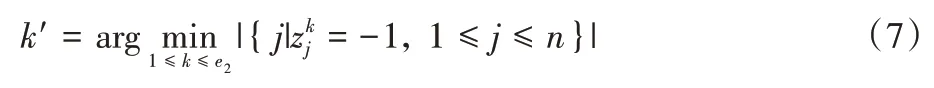
算法2 描述了基于DBSCAN 技术拾取初至波的过程。第1）行根据式（5）～（6）执行DBSCAN 聚类；第2）～6）行根据定义2 计算每个簇的分割线；第7）～8）行根据式（7）选择最完整的分割线作为初始初至波；第9）行返回找到的初始初至波F。

3.2 微调阶段

本节详细描述了采用局部线性回归和能量比值最小化技术的初至波微调阶段。局部线性回归技术用于补齐缺失值，能量比值最小化技术用于调整错误值。

3.2.1 局部线性回归补齐缺失值

由于找到的初始初至波在部分道上可能存在缺失值，在本节中，根据相邻道初至波相关性强的特点设计了一个局部线性回归模型来补齐缺失值，回归方程定义如下：

其中：α和β是回归系数。

该算法的目标是最小化真实值y和预测值之间的差值，建立损失函数模型：

根据一阶最优性条件，将式（9）分别对α和β求偏导，并令其为零，得到回归系数：

通过回归模型，可以计算出回归系数α和β的值，从而计算出缺失道所对应的预测值。最后，将得到的预测值作为该道的初至波。

算法3 描述了通过局部线性回归补齐缺失值的过程。第1）行初始化F′；第2）行定义了循环范围；第3）行判断当前道是否存在缺失值；第4）行定义了长度为2×τ的数组x和y；第5）～9）行将缺失值前后各τ道邻居初至波所对应的地震道数和初至波位置分别赋值给x和y；第10）～11）行根据式（10）和式（11）计算回归系数α和β的值；第12）行根据式（8）计算第j道的预测 值；第13）行更新第j道的值；第16）行返回补齐缺失值后的初至波F′。

3.2.2 能量比值最小化调整位置

由于初至波的能量值通常较大，在本节中，设定阈值ε作为能量值的约束条件，采用能量比值最小化技术对小于ε的初至波位置在初至波范围内进行调整。根据初至波的特性，设定如下的优化模型：

其中：E(low，high，j)=代表第j道的第low～high个样本点能量之和；λ是初至波范围；是第j道的初至波范围；θ是能量比值的窗口长度；ε是能量阈值。

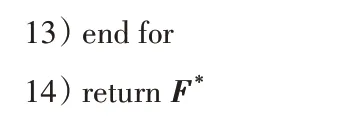
算法4 描述了用能量比值最小化技术对初至波能量值小于ε的位置进行调整。第1）行定义了循环范围；第2）～12）行是调整过程，第2）行判断初至波能量值是否达到调整条件，小于ε才调整；第3）行初始化目标函数的最小值；第4）行是在第j道的初至波附近滑动；第5）行根据式（12）计算能量比值；第6）行判断目标函数值和约束是否达到更新条件；第7）～8）行更新目标函数值和最小能量比下标i*；第11）行更新调整后的初至波位置；第14）行返回调整后的初至波F*。

4 实验与结果分析

为了验证算法的有效性，本文将FPCL 与改进的能量比（Improved Modified Energy Ratio，IMER）法［8］、互相关技术（Cross Correlation Technique，CCT）［10］、基于模糊C均值聚类的微震数据自动时间选取算法（Automatic time Picking for microseismic data based on a FuzzyC-means clustering algorithm，APF）［12］、基于两阶段优化的初至波自动拾取算法（First-arrival automatic Picking algorithm based on Two-stage Optimization，FPTO）［16］共四种算法在两个地震数据集上进行测试。其中，IMER 是以单道为基础的能量比法，CCT 是以多道为基础的互相关法，APF 是以整个数据集为基础的聚类算法，FPTO 是两阶段优化算法。实验结果表明FPCL 更准确。

4.1 数据集

表1 列出了实验所用的两个数据集的相关信息。

表1 地震数据集信息Tab.1 Seismic dataset information

4.2 参数敏感性分析

为研究参数对算法性能的影响，本文分别测试聚类中心个数e1、邻居通道数τ、初至波范围λ和能量比值窗口长度θ对各数据集准确率的影响。该实验基于单变量方法进行测试，即固定其他参数来研究一个变量对结果的影响，实验结果展示在图2 中。

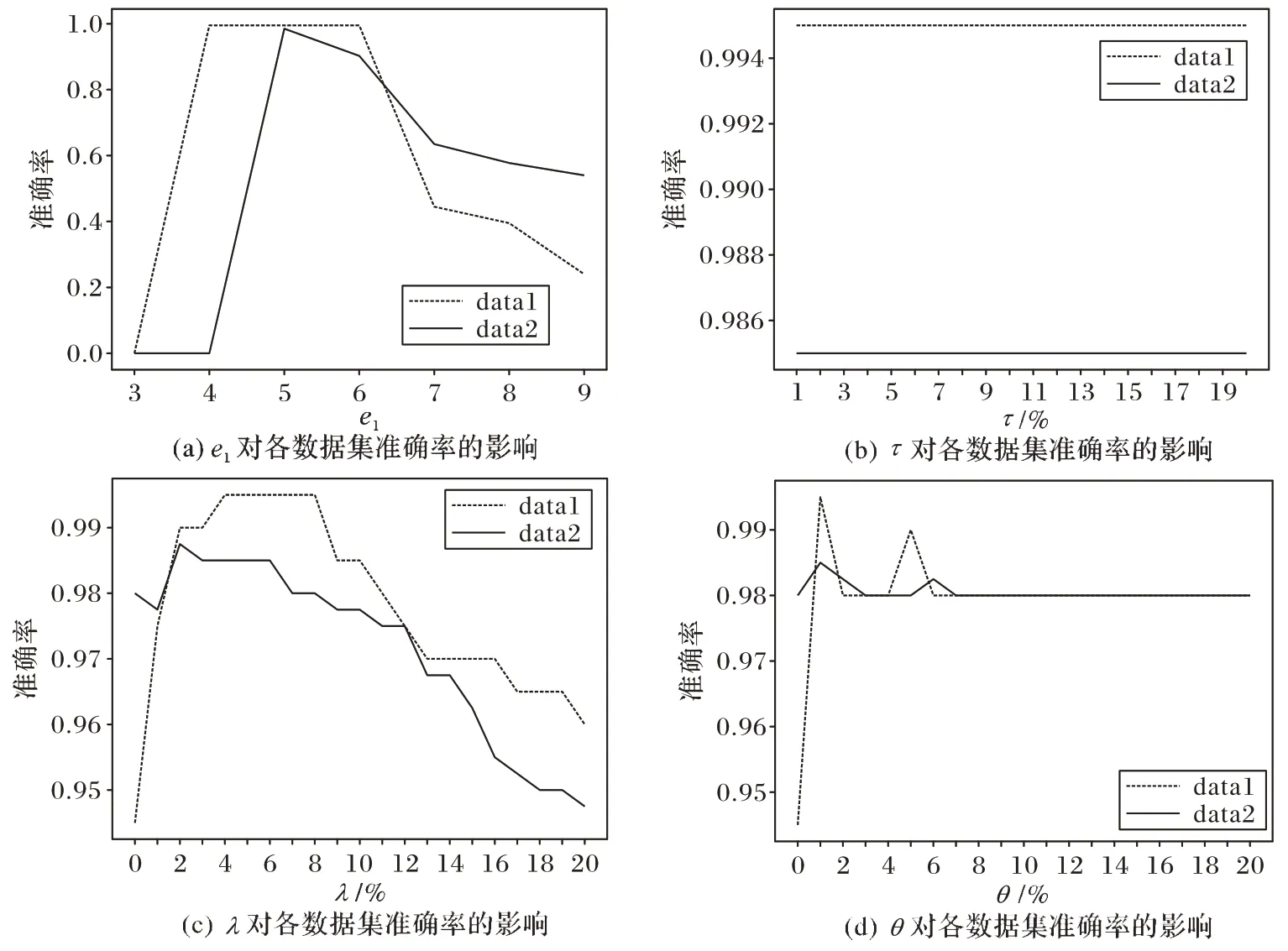
图2 参数对各数据集准确率的影响Fig.2 Influence of parameters on accuracy of each dataset

4.3 实验参数设置

根据图2（a）的实验结果，聚类中心个数e1=5.00 是最佳设置；图2（b）的结果显示邻居通道数τ对实验结果的影响不大，本文将τ设置为地震道数的5.00%；λ和θ与每道的数据规模有关，根据图2（c）和（d）所示，λ的最佳设置为数据规模的4.00%～6.00%，θ的最佳设置为数据规模的1.00%；能量阈值ε由几个实际地震数据的初至波计算得到，选取实际地震数据的初至波，发现初至波的能量值通常都大于0.20，因此本文将ε=0.20 设置为初至波能量值的约束条件。

4.4 实验结果描述

图3 描述了在data1 上的初至波拾取过程。图3（b）表示基于k-means 聚类后选择的初至波簇，图中的点表示簇中元素，右上角的是噪声，和初始数据集相比，此时的数据量从300 200 减少到14 335。图3（c）表示基于DBSCAN 在图（b）中拾取的初始初至波，红色的点表示初至波位置，从图中可以看到，它的拾取结果对噪声不敏感，但部分道存在缺失值和错误值。图3（d）表示用局部线性回归和能量比值最小化技术来补齐缺失值和调整错误值后的初至波。

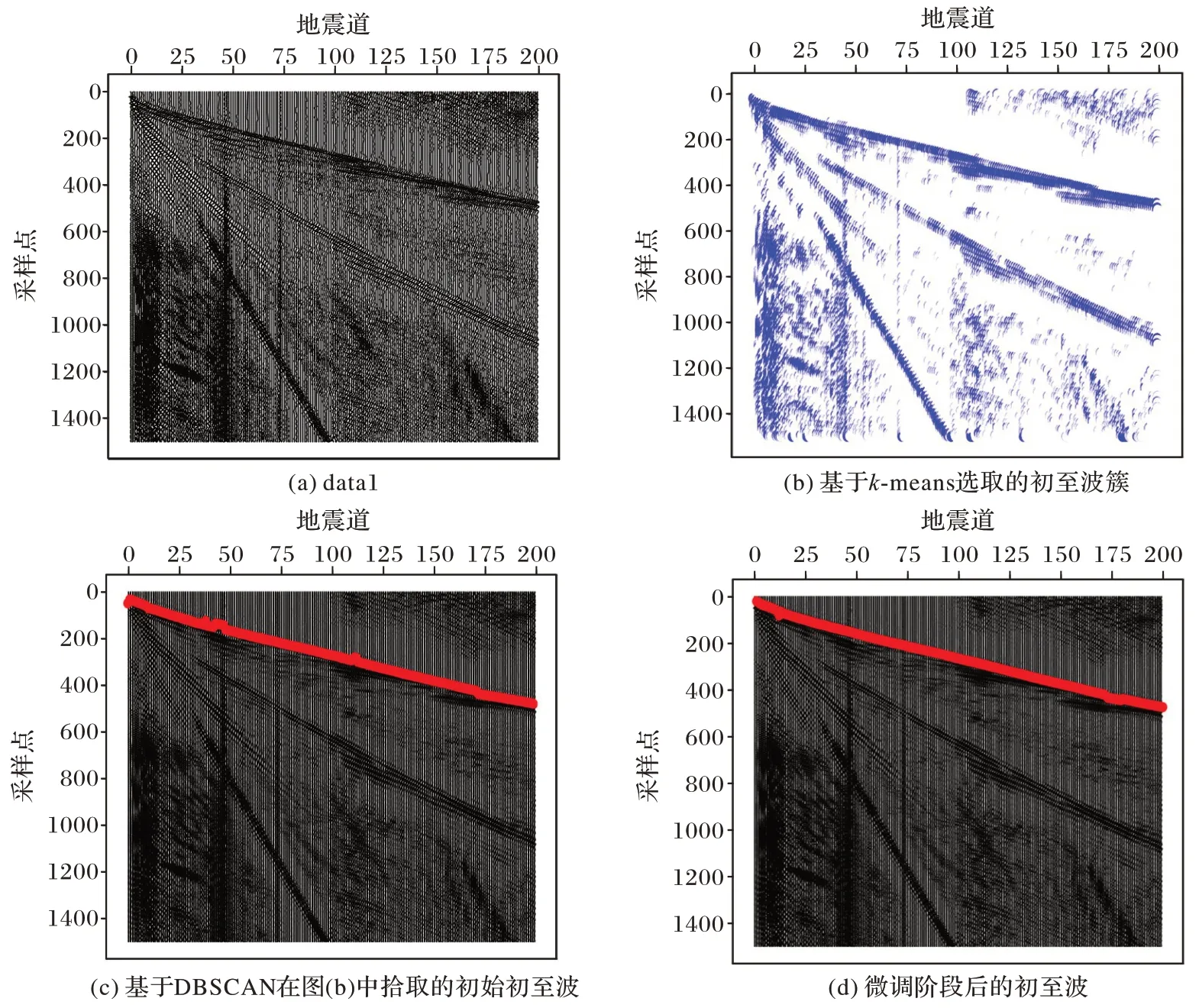
图3 在data1上的初至波拾取过程Fig.3 First-arrival picking process on dataset 1

图4 描述了在data2 上的初至波拾取过程。图4（b）表示基于k-means 聚类后选择的初至波簇，图中的点表示簇中元素，左上角的点是噪声，和初始数据集相比，数据量大幅度减少（从600 400 减少到27 020）。图4（c）表示DBSCAN 技术在初至波簇中拾取的初始初至波，红色的点表示初至波位置，从中可看出拾取结果对噪声不敏感，但部分道还存在缺失值和错误值。图4（d）表示用局部线性回归和能量比值最小化来补齐缺失值和调整错误值后的初至波。

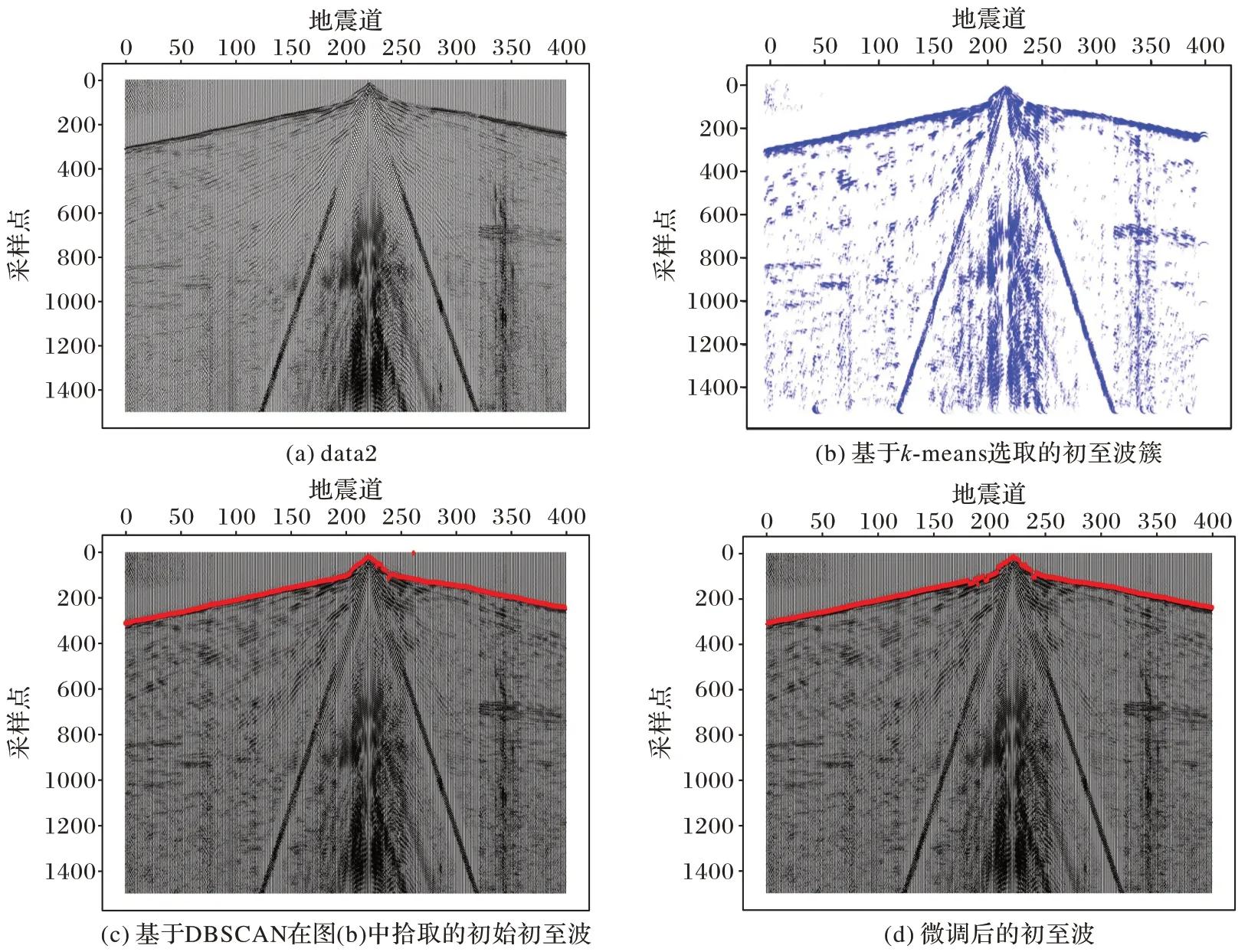
图4 在data2上的初至波拾取过程Fig.4 First-arrival picking process on dataset 2

4.5 实验结果与分析

将FPCL 与IMER［8］、CCT［10］、APF［12］和FPTO［16］四种算法进行对比：IMER 用多个窗口代替了传统的两个窗口来拾取初至波；CCT 通过互相关技术来检测初至波；APF 使用模糊C均值聚类来区分初至波和噪声；FPTO 采用两阶段优化拾取，先用滑动窗口找出初至波范围带，然后改进了能量比率算法在范围带中拾取初至波。

图5 展示了五种算法在两个数据集上的拾取结果，黑色方框内为正确的初至波拾取结果。图5（a）表示在data1 上的拾取结果，由于APF 的抗噪能力较弱，因此在强噪声的情况下，拾取结果会早于初至波；除此之外，和初至波相比，CCT获得的结果会有所延迟。图5（b）表示在data2 上的拾取结果，在该数据集中，CCT 的偏差较大；IMER 和APF 只在较少道上存在偏差；FPTO 受噪声干扰，拾取结果不准确。

图5 五种算法的拾取结果Fig.5 Picking results of five methods

本文在两个地震数据集上计算了这些算法的准确性，实验结果的准确率对比如表2 所示。从表2 可看出：FPCL 与IMER 法相比，准确率分别提升了4.00 个百分点和3.50 个百分点；与CCT 相比，准确率分别提升了38.00 个百分点和10.25 个百分点；与APF 相比，准确率分别提升了34.50 个百分点和3.50 个百分点；与FPTO 相比，准确率分别提升了5.50 个百分点和16.25 个百分点。上述实验结果表明FPCL的准确率更高，找到的初至波位置更加准确。

表2 不同方法在两个数据集上的准确率对比 单位：%Tab.2 Accuracy comparison of different methods on two data sets unit：%

5 结语

目前，拾取初至波算法受到背景噪声和复杂近地表条件的干扰，拾取精度会降低。本文提出了由两阶段组成的FPCL。由于DBSCAN 具有传递性且抗噪能力强，适合拾取初至波，但直接在整炮数据上运行其时间复杂度较高，因此，本文利用k-means 时间复杂度低的优势，预拾取阶段先基于k-means 找到初至波簇，再基于DBSCAN 在初至波簇中进行拾取，通过结合这两种聚类算法的优点来选取初始初至波，这种方式可以提高抗噪能力和运行速度。微调阶段通过局部线性回归和能量比值最小化技术来补齐缺失值和调整错误值，可以进一步提高准确率。

在两个数据集上的实验结果表明FPCL 可以有效地拾取初至波。将来，会考虑将FPCL 运用到其他方面，例如信号处理和地震数据去噪。