支持零知识证明的交易数据隐私保护方案*
2022-02-28马兆丰段鹏飞罗守山
秦 捷,马兆丰,段鹏飞,罗守山
(北京邮电大学 网络空间与安全学院,北京 100876)
0 引言
由于传统区块链系统在链上数据完整性和安全性方面存在局限性[1],且链上与链下的数据无法进行高效协同。因此,本文提出在提供隐私保护的同时保证链上与链下数据的强关联性。采用零知识证明、链下计算等技术来解决数据协同的关键性问题,最终实现区块链性能拓展与安全性能的提升。将链下的交易数据生成零知识证明并置于区块链中存储,达到隐私保护的效果。
区块链是运用密码学技术将区块以链表形式联系起来,由众多参与者一起完成并维护的分布式账本[2],由于具有去中心化、不可篡改等特点,使其在近几年受到更深入的研究与使用。其中,以联盟链为框架的区块链平台(例如Fabric)在国内得到了越来越多的研究与实际上的应用开发,然而联盟链中的账本交易数据对于每个参与维护区块链的组织来说是公开透明的,这意味着每个组织都能够看见链上每个用户的交易信息。用户的交易等隐私信息很容易被泄露,这对于一些特别注重隐私性的行业是不能够接受的[3]。
因此,在既可以实现区块链去中心化的功能同时也可以对链的信息进行安全性的保障是本文研究的重要课题。问题的处理关键在于,交易底层的区块链信息和实际应用层间的传输接口隐私保密度,以及处理交易的智能合约的可验证度。针对与基于零知识证明的隐私保护有机结合的问题,本文在研究同态的Paillier算法的基础上,给出了与零知识验证结合的区块链隐私保护方法。
零知识证明是属于当前区块链链下Layer2扩容的一种技术路线,其利用零知识验证进行链下的安全运算形成数据,随后再将计算结果交给链上的智能协议验证,以建立链下计算链上验证的隐私防护系统[4]。零知识证明技术尽管在一些数字货币如Zcash、Monero中有了广泛应用[5],但其对数据所产生的智能合约证明的效率仍然比较慢。基于此,将数据利用零知识证明和链下的加密算法形成证据,然后将计算结果交给链上的智能合约验证,以建立链下计算链上验证的隐私与安全体系[6]。
随着数据时代的到来,本机处理数据的负载也越来越大。而云计算的发展很好地解决了对数据计算处理的效率问题,但将数据外包给第三方服务器进行加密很有可能造成数据泄露,因此本方案结合安全多方协议,在云服务器上对数据高效计算的同时保证数据的隐私性。
在基于零知识证明的链下计算链上验证的拓展架构方案中,会面临分布式存储可能带来的风险,使得这种链上存证链下计算面临越来越复杂的安全考验,同时也增大了数据丢失与链上链下数据不协同带来的不确定风险。因此,如何在功能拓展的同时确保链上链下数据协同统一,规避数据在管理过程中的风险问题是架构需要着重讨论的内容。
针对这一难题,一般给出的解决方案是对数据在链下进行计算、生成证据、加密等处理后再上传,这其中就包括上面所提到的零知识证明的隐私保护相关理念与保护手段[7]。但区块链与传统的隐私保护机制不同[8],如果直接对数据进行加密处理后再上传可能会导致整个链上交易无法完成共识,即便使用零知识证明技术在加密算法环境下满足了隐私安全的需求,但是链上数据的协同一致性也会大打折扣。
基于此背景,对于区块链链上数据与链下数据存储相结合的可拓展性研究逐渐受到关注。Niu等人[9]将可搜索加密方案应用到了区块链架构上,通过区块链实现了不信任的多方间建立可靠数据共享的方案,然而该方案基于复杂的索引与排序算法进行设计,所以计算开销过大。文献[10]提出了一种区块链多授权可搜索的属性基加密方案,并结合布隆过滤器与可搜索加密减少链上搜索时间,但只能在簇内可信的机制下适用。以上方案在安全性和开销效率之间的平衡难以得到解决,所以需要一种解决方案来满足两者之间的需求平衡。让链上服务回归链上,链下服务回归链下,实现链上链下数据协同,提出链上链下协同一致的方案,以达到区块链的高可用性、高安全性和高拓展性[11]。
本文主要的研究工作如下:(1)研究基于零知识证明的数据上链机制和链下计算技术,实现隐私保护功能,提高交易数据的隐私保护能力。(2)提出基于区块链的数据协同模型,构建一种基于区块链的安全可控数据协同技术架构,以此保障交易数据流通中的隐私安全。
1 预备知识
1.1 区块链
区块链科技的源头是以比特币为代表的加密货币[12],由化名为中本聪的学者在Bitcoin:A Peer-to-Peer Electronic Cash System中提出关于区块链的概念,是指一个可以根据时间序列将所有储存数据的区块以链表的形式组织的数据结构体[13]。它可以通过使用密码学维持一个去中心化的账本,而这种账本的各节点间的信息共享关系是无法修改并且也不能进行伪造的。这样的结构形成了一个去中心化的分布式系统,存储每个节点的历史交易记录信息,所有节点通过共识机制来保证数据库上数据的一致性,并使交易具有可追溯和不可逆转的特性[14]。区块链技术最初是用于记录比特币等加密货币交易的数据结构,加密货币的技术原理是利用区块链的分布式网络基于密码学算法来生成的,代表着区块链技术的1.0时代——数字货币时代[15]。 随着数字加密货币技术平台的发展,后来在数字货币的基础上加入了智能合约的概念,代表着区块链技术的2.0时代[16]。与加密货币相关的底层技术逐步改进形成了区块链技术,如今在其他领域也展现出迅猛的发展势头,在各个行业与领域中进行智能化应用的开发,代表着区块链发展进入到3.0时代[17]。
1.2 零知识证明
零知识证明技术,最早是由Goldwasser等人于20世纪80年代提出的一种最小泄露证明。其设计理念与证明思想被广泛应用于身份证明、电子现金、数字签名等场景。
通常来说,零知识证明的初始化过程包括以下几个步骤[18]:
(1)声明:证明方根据论断内容产生一些派生的数据,然后把它们发送给验证方。
(2)挑战:验证方利用断言产生一些等价问题,然后把这些问题发送给证明方。
(3)响应:证明方求解这些等价问题,然后把对应的解答返回给验证方(但验证方无法利用这些等价问题的解答获得原问题的解答)。
(4)验证:验证方判断那些等价问题的解答是否正确。
初始化算法:Setup(1λ)→str,输入安全参数λ,输出公共字符串str。
证明算法:Prove(str,ι,ω) →π,输入公共字 符串str,语句ι∈L(其中L是NP Language),证据ω,输出证明π。
验证算法:Vrfy(str,ι,ω)→b,输入公共字符串str,语句ι,证据ω,输出布尔变量b∈ { 0,1},判断输入证明语句ι是否成立。
检查算法:Check(str,ι,ω)→d,输入公共字符串str,语句ι,证据ω,输出布尔变量d∈ { 0,1},判断ω是否使得ι成立。
1.3 Paillier算法
Paillier加密算法是Pascal Paillier在1999年发明的概率公钥加密算法。优点是原理简单、易实现,缺点是仅支持加法运算。
(1)密钥生成:先随意选定两个大素数p和q,运算出它们的积n=pq和最小公倍数λ=lcm(q− 1,p− 1)。选择随机数g,且满足最大公约数gcd(L(gλmodn2),n)=1。定义L(x) = (x− 1)/n,存 在u=(L(gλmodn2))−1。此时得到公钥为(n,g),私钥为(λ,u)。
(2)加密:对于明文m,明文信息需要满足m小于n,选择一个随机数r (3)解密:对于密文c,明文m=(L(cλm modn2) /L(gλm o dn2)) modn。 同时,Paillier也存在快速生成密钥的算法:在密钥长度相同的情况下,可以快速生成密钥g=n+1,λ=Φ(n),u=Φ(n) − 1modn。所以n更像是加密环境值,g对应密钥。 星际文件系统(Inter Planetary File System,IPFS)是一种点对点的分布式文件系统,同样具有去中心化存储的特性,因此与区块链具有较好的结合性,同时也可以较好地解决当前区块链中区块存储容量存在限制的问题[19]。 目前有一些与区块链和IPFS相关的研究,王路阳等人[20]提出了一种基于区块链和IPFS网络的监控信息隐私保护机制。该方案结合IPFS和区块链技术,解决了监控管理中的隐私保护问题。其中区块链用于安全存储带有哈希的信息,并为哈希值提供验证信息,IPFS用于存储和分发监控信息。Hao等人[21]针对农产品可溯性管理中数据可能被篡改从而影响食品安全的问题,提出了一种基于IPFS的区块链存储模型。该方案主要用于存储不同环节中农产品的信息,该方案存储数据完全公开透明,虽然通过区块链保证了数据不被篡改,然而并未考虑存储数据的安全问题。 有关区块链和IPFS技术的应用结合问题还处在理论研究的起步阶段,许多方案还未得到实际的应用和落地[22]。因此区块链和IPFS技术的应用结合仍然任重而道远,相关应用的探索还要一直持续,但是可以为两者的进一步实质性结合提供借鉴价值。 在数据存储和共享上,IPFS能够处理重复冗余的数据文件,把相同的文件合并,减少了数据复杂程度,节省了服务器的存储资源。对上传到IPFS的数据文件进行加密和哈希函数处理后,都会生成唯一文件哈希密文值。哈希密文值唯一指定了数据文件,对数据信息进行修改后就会重新获得更新的不重复的哈希值。在获取文件时,IPFS进行用户访问权限控制,完成验证后根据密文哈希值从分布式存储节点中返回解密之后的内容。 基于目前的零知识证明技术现状[23],针对基于零知识证明的交易数据隐私保护的工作可以从零知识证明的区块链隐私保护、加密后数据的链上链下一致协同两方面展开。 本文基于零知识证明的交易数据隐私保护模型如图1所示。方案设计包括区块链、交易存证服务、零知识证明算法和同态加密算法创建隐私保护模型,以实现区块链系统中的交易安全与隐私保护。 图1 链上零知识验证模型 基于区块链的隐私保护方案的设计包含5个对象:交易双方、智能合约、区块链网络与密钥管理方。交易双方包括交易生产者和消费者。智能合约预先设置包含零知识证明验证的触发条件,在去中心化的前提下判断零知识证明证据及承诺的有效性。参与共识的组织节点利用验证密钥(Verification Key,VK)对交易双方提出的交易内容进行零知识电路校验,以确保区块链上信息的完整性与一致性。密钥管理方有一种绝对可信的机制,来产生证明密钥(Proving Key,PK)与VK进行零知识证明。 本文在经典同态加密算法Paillier算法的基础上,研究了能够进行零知识证明验证并能够对用户隐私交易数据进行保护的方案算法[6,18],并对其进行数据协同方面的改进。该算法能够在不透露交易双方所有交易细节的情形下,通过智能合约系统确认双方之间交易内容的合法性,同时能够独立对用户的隐私数据进行加密处理。若验证未通过,则用户可能发起了恶意交易并向应用端返回错误处理信息,否则将此次交易结果写入区块中。 设计和构建基于零知识证明的简洁非交互式知识验证系统需要进行信息证明,例如范围证明和相等性证明,并对此次产生的数据和承诺证明进行加密操作。在完成交易数据初始化和证明生成之后,与链上部署的智能合约进行交互。通过加密和零知识证明处理之后的数据校验方法,可以在不向各节点提供交易细节的前提下,检验交易合规性。在共识验证通过后,交易双方的交易数据密文上链存储到区块中。 在设计方案中,交易双方在区块链网络中进行P2P通信。为了不泄露交易隐私,交易双方各自生成零知识证据和承诺,并对这些承诺和交易数据进行加密;密钥管理方为本次交易生成新的证明密钥与验证密钥,证明方向智能合约提交证据以进行验证;最后,如果认证成功,将本次交易上块,否则予以撤销。认证者在不接触交易数据的前提下进行了本次交易的认证,保障了交易双方的信息安全。 2.2.1 零知识证明过程 本方案中交易双方的交易过程在应用层进行,为了确保交易过程中的隐私不被泄露且支持智能合约端对密文的零知识证明验证的合法性,应用层除了为交易双方进行同态加密产生密文,还须产生零知识证明对应的相等性证明和范围证明证据。然后将上述信息和经过加密后的成交数据发送到交易层的链码端,链码端负责对本次成交的有效性加以检验。 基于交易数据的零知识证明框架主要分为以下5个步骤,如图2所示。 图2 零知识证明生成过程 (1)问题转换:由于非交互式零知识验证不能直接应用于计算,因此为了围绕这个问题进行证明,需要将要证明的问题的陈述转化成零知识证明能够理解的形式,即二次算术程序,可以解决所有基于算术电路的多项式复杂程度的非确定性(Non-deterministic Polynomial,NP)问题的证明和验证。将表示计算式的电路问题转换为一阶约束系统(Rank-1 Constraint System,R1CS)(向量点积形式),以构造完整的零知识证明交易框架。 (2)生成多项式:将生成的R1CS向量表达式转换为多项式二次算术程序(Quadratic Assignment Problem,QAP)问题以实现对上述电路问题的证明验证,这一步骤主要完成待证明计算式验证和多项式验证之间的等价转换。 (3)引入约束:完成问题到多项式证明的转换后,需要再引入包括椭圆曲线密码体系下的系数知识假设等约束,限制证明者在证明生成过程中的参数使用,防止证明者使用不符合约束条件的多项式进行恶意攻击。 (4)信任初始化:在进行证明和认证之前,需要设置和生成一些公共的参数,例如通过密钥管理方为交易生成公共参数,为交易双方提供证明密钥和验证密钥。 (5)使用PK生成承诺和证据:区块链验证节点使用VK对证明者零知识承诺信息和零知识证据进行验证。 2.2.2 安全多方计算过程 安全多方计算过程如下文所述。 (1)参与方使用密钥生成算法生成公私钥对(Pub,Prv)。 (2)参与方将输入经过同态加密处理后产生的密文发送给服务器。 (3)云服务器接收到密文后,使用安全多方计算协议进行处理,得到y→f(c1,c2,… ,cn)。 服务器在对安全多方计算流程中得到的结果进行同态计算得到Eval(y”) → (y”1,y”2,… ,y” n),并将结果返回至对应的参与者。 2.2.3 数据协同过程 在链下通过零知识证明验证和同态加密对数据实现了隐私保密,为保证通过零知识证明验证和同态加密的数据保持链上和链下的协同安全,基于区块链隐私保护的数据协同方法还采用了星际文件分布式数据存储体系IPFS。 方案模型结合了区块链、IPFS、智能合约以及前面提到的零知识证明和同态加密Paillier算法,以达到保护数据隐私,实现数据在协同一致中的安全共享。利用链下的分布式数据体系的方法保存数据信息,将文件数据本身保存在IPFS中,而加密后的哈希值等元信息则成为IPFS的键值保存在区块内。通过这样的方式实现了数据的协同一致。并按照交易逻辑使用智能合约系统进行相关处理,以得出数据处理结果,在数据存储的过程中实现链上数据与链下存储的协同一致,避免数据隐私泄露。 本节对李龚亮等人[6]提出的支持零知识证明的同态加密(Homomorphic Encryption Based on Paillier and Zero-Knowledge Proof,HEPZP)算法进行描述及实现,并从密文性验证和数据协同方面对其设计进行改进,以更好地应用于区块链上的交易数据服务。 算法公式中涉及的参数如表1所示。 表1 方案相关参数 3.1.1 系统参数生成 区块链系统中拥有一份独立的系统参数,且该参数在区块链系统初始化存储在账本后便不可篡改,在整个系统的生命周期中保持不变。系统参数在交易过程中为交易双方提供公私钥生成、交易密文生成以及零知识证据产生等功能。 选取两个较大的素数p和q,计算两者的乘积n和(q− 1,p− 1)的最小公倍数λ,定义式L(x) = (x− 1)/n。在Zn*2中选择阶很大的元素g1以满足的最大公倍数为1,即互素。计算系统参数。指定随机数r 3.1.2 公私钥生成 每个参与交易的用户需要持有一对由系统生成的公私钥。其中,公钥作为用户的唯一标识,可当作每一个用户的交易地址,而私钥由用户自己保存,并需要确保私钥的隐私安全性。 选择随机数v 3.1.3 加密过程 当交易双方都需要完成交易过程时,应用层要求对交易中的有关数据和交易信息进行加密,然后再发送到链码端。加密过程如下文所述。 对于明文m 获得4份密文c=(c1,c2,c3,E),其中E与零知识证明证据的生产有关,其加密函数也记 为Enc(m,r0,r1,Pub,P)。 3.1.4 解密过程 对密文c来说,需要对明文数据m和用来为链码端创建相等性证据的r0进行解密。 解密m:使用系统参数P中的(n,h)和私钥v,以及密文中的 (E,c1),先从密文中提取明文数据对应的加密结果cm,再计算得到原始明文: 解密r0:使用系统参数P中的(n,h)和私钥v,以及密文中的 (c2,c3),从密文中提取出随机数对应的加密数据cr0,并计算得到原始数据: 解密函数分别记为Decm(c,Prv,P)和Decr0(c,Prv,P)。 3.2.1 相等性证明 (1)应用端使用交易双方选取的随机数(r0,r1),以及产生的交易金额密文ct。 (2)根据密文为交易双方生成承诺E和F: 式中:a为参数;b为余额;t为交易的金额。 (3)根据承诺E和F产生相等性证据。 (4)智能合约通过承诺和相等性证据,以及双方的公钥和系统参数完成相等性证明过程。 3.2.2 范围证明 交易金额大于0证明如下: (1)应用端使用交易双方选取的随机数(r0,r1),以及产生的交易金额密文ct。 (2)根据上述步骤(1)中随机数密文产生承诺E,如式(9)所示。在范围证明中,参数a的绝对值需要大于或等于1。 (3)承诺产生范围证据。 (4)智能合约端通过承诺与范围证据,以及消费者的公钥和系统参数完成校验。 交易余额大于0证明如下: (1)应用端使用交易双方选取的随机数(r0,r1),以及产生的交易金额密文ct,消费者的输入金额密文ca。 (2)解密出输入金额密文ca的明文以及产生输入金额密文ca时的随机数r0in。计算剩余金额s=in−t。计算加密剩余金额的随机数r0s=r0in−r0t。 (3)利用同态加密加法同态的性质获得交易余额的加密密文cs。 (4)根据上述步骤(1)中随机数密文产生承诺E,如式(9)所示。 (5)智能合约端通过承诺与范围证据,以消费者的公钥和系统参数完成校验。 3.2.3 密文正确性证明 验证过程的实现,需要在链上部署证明方的链码,证明方将经过智能合约验证后的证据承诺与链码本身交由区块链网络节点验证,并根据数字签名或数字证书进行身份验证,完成交易的零知识验证。区块链网络共识的其他节点也可通过链码进行参与。需要验证在同态加密Paillier下密文的正确性。 给定密文c和证明密钥PK,证明者需要证明其知道明文m和随机数 (r0,r1),使得密文c=Enc(m,r0,r1)。 证明者随机选择 (m”,r0”,r1”),并计算c=Enc(m”,r0”,r1”)。 验证者生成挑战变量e,令证明者计算出明文和随机数对应的证据为 (z1,z2,z3),其中z1=m”+em,,并发送给验证方。 验证者计算Enc(z1,z2,z3),如果Enc(z1,z2,z3) 等同于c”⋅ce,则验证成功。 对于交易双方给出的承诺和证明,区块链的各节点加以验证。只有当每个产生的证明都经过智能合约验证后,本次交易才验证通过。当该交易通过区块链运行的共识方案后,即可写入到区块中。 交易方案的过程主要包括应用层和链码端两部分,假设消费者向生产者发起交易,则应用层步骤如下: (1)得到消费者的公钥和私钥,作为被转账方的生产者仅需提供公钥而非私钥和系统参数P,通过两者的公钥Pub对交易输入进行加密,产生交易输入密文。 (2)产生的交易数据仅能够通过交易参与者的私钥Prv才能解密查看,因此通过消费者的私钥和系统参数对所有交易输入信息进行解密,并计算交易余额。 (3)基于方案的零知识证明算法来生成可信任不被泄露的零知识交易证据,同时对交易输入输出金额密文上的承诺形成范围验证和相等性证明。 (4)发送到区块链网络其他节点的交易数据需要由参与双方进行数字签名,并将密文和零知识证据相关承诺发送到链码端,请求本次交易校验。 在此过程中,必须要在链下对数据进行零知识证明的证据产生和同态加密之后,再对数据进行上链操作,方案中使用的加密算法是零知识证明应用于同态加密Paillier算法得到的,数据上载存储则是在区块链运行的智能协议中,添加将加密后的哈希数据保存在IPFS的流程,部署智能合约并同步到区块链网络。 算法1:上传数据upload 根据算法对文件中记录字段进行加密,得到密文计算结果C”: 式中:dh为记录字段的第h条记录;PKHE为算法的证明密钥;rh为对记录字段加密过程中产生的随机数。 generate(X)为用户X生成密钥。该设计中采用上文提到的公私钥生成算法生成非对称密钥。非对称密钥中的公钥用于对信息加密,私钥用于对信息解密。 write(Y)将信息Y的内容写入IPFS中,Y中包含区块字段的所需信息,生成对应的区块字段。 check(X)用于验证角色的权限,查看当前用户是否可以读取监控信息。 hash(F)计算文件数据哈希值,将信息F进行哈希函数计算后得到一串哈希值。 设计的模型中,生产者在上传数据时可以根据合约内容对文件数据进行加密,并由链码端将数据密文存储到分布式文件系统中,并向生产者用户返回相应哈希值。同时合约也会将产生的哈希值信息等同于交易上链。此后,消费者根据哈希值在IPFS系统中进行交易数据的查询。 (1)隐私性:数据加密是保证隐私数据安全性的基本要求。方案采用了将同态加密Paillier算法和零知识证明相结合的方式对数据进行加密后的储存。在各区块链节点的智能合约终端查看到的所有交易数据全部处于密文状态。利用链下算法处理应用数据在链上公开的隐私泄露问题,维护交易数据的隐私性。 (2)真实性:数据内容在区块链储存流程中与生产者进行绑定,将数据文件存放到IPFS中,而相应的数据内容哈希值在经过对生产者的私钥密码进行签名后,进行区块链上持久化且不可篡改的储存,以保证数据内容哈希值与生产者之间的一一对应,因为数据内容修改会导致相应的数据内容哈希值发生变化,所以在数据发生变化时可以根据哈希值判断是否发生了攻击篡改。 (3)防抵赖性:将参加交易过程的每个用户产生的交易信息都同等存储在链上,同时基于区块链可溯源和不可篡改的特点,对数据共享流程进行跟踪溯源,实现了防抵赖性功能。 (4)零知识性:零知识性是指在证明者Prover与验证者Verifier的交互过程中只通信正确的知识,不会泄露额外的信息。系统参数为公开值,证明者Prover向验证者Verifier发送的签名函数称为正确的知识证据,验证者返回给证明者的随机数c称为验证挑战,证明者接收到随机数c后回复验证者的知识证据 ()signr称为应答。在证明过程交易双方的交互中,没有向其他用户和节点泄露交易的细节,因此具备零知识性。 为了验证论文提出的基于同态加密和零知识证明的同态加密算法的性能,本章采用联盟链中的Fabric项目对该算法进行实现。在完成对基于Fabric 2.2版本的联盟链系统的环境搭建后,本章对算法的实现效果进行了测试,以验证算法的可行性和测试该算法的实现效率。 本文的仿真实现实验在虚拟机中进行,采用的虚拟机是VMware,机器配置处理器内核4个,内存6 GB。在虚拟机中采用Ubuntu16.04操作系统,所需的环境配置包括go1.15.9、docker20.1.7和docker-compose1.29.2等服务。本文零知识证明隐私保护方案中涉及的智能合约采用go语言进行编写。 功能性测试主要包括数据加密成功测试、零知识验证测试和数据真实性测试3个部分。 测试过程中链码实例化为用户A在账本中存储密文50的金额,然后向另一用户B发起转账10的交易。在正确的交易过程中,为用户A生成一个密文金额为40的余额,为用户B生成一个密文金额为10的转账金额。将生成的密文信息与零知识证明证据发送至链码端验证,通过在节点中查看容器日志可以发现链码端出现的交易信息均为密文状态,同时也通过了各种零知识证明的验证,并向应用端返回交易成功的信息。 通过使用用户私钥修改链下IPFS系统存储的信息模拟恶意用户篡改攻击。经过链下链上的协同验证,发现此时链下信息计算生产的哈希值发生了改变且与链上存储的哈希值不相同,以此来确定该数据被攻击篡改,保障了数据的真实性。 在功能性测试中,当应用端正确计算交易结果时,链码端还可在交易数据是密文的情况下对交易结果进行检验,并能够验证通过,将交易结果密文保存在账本中。在测试过程中,当应用端提交一次恶意交易时,如用户使输出金额大于输入金额,这样虽然在应用端可以生成相应的密文信息和零知识证据,但是在链码端却无法利用这些证据完成校验过程,所以链码端可以判断此次交易为恶意交易,拒绝将这次的交易结果写入账本。因此,在区块链的交易中使用本文算法不仅可以对交易双方的信息进行保密,避免用户隐私泄露,同时还能够在链码端进行零知识证明验证,保证交易过程的合法性。 效率测试是指对算法的密钥生成、加解密过程和零知识证明密文正确性验证过程进行测试,并与Paillier算法进行对比。算法的稳定性主要是建立在离散对数的计算方面,当使用的密钥长度足够大时,根据密码分析理论可以确保算法不被轻易攻击破解。 本文实验分别对系统参数中的密钥长度n取长度为1 024、2 048、4 096位进行测试,由于4 096位的长度基本已能够保证本文算法的安全性,这里便不再对更大位数的n进行测试。在实验过程中,对每个长度的密钥进行多次独立的实验,每次得到的实验结果都相对稳定趋于确定的值,最后进行多次仿真实验后记录实验数据并取平均值绘图记录,如图3~图6所示。 图3 不同密钥长度密钥生成时间 图4 不同密钥长度加密时间 图5 不同密钥长度解密时间 图6 不同密钥长度零知识密文验证时间 零知识证明算法与Paillier算法在同样实验条件下的测试结果表明,虽然实验中本文零知识证明算法的加解密时间比Paillier算法耗时稍长,但在实验所使用的密钥长度下的结果相差并非很大,当密钥长度达到4 096位时加解密的相差范围在20~50 ms,而此时4 096位密钥在应用中已经达到很高的数量级。此外,在密钥生成时间下,相较于Paillier算法,零知识证明算法耗时较少,在4 096位的密钥长度下相差的时间达到了秒级。在智能合约端对密文验证时间进行测试,结果表明:即使在密钥很长的情况下,验证时间也可以保持在1秒左右,在正常的密钥长度下,零知识证明过程均能够在毫秒级别被完成。 区块链去中心化的特征,促使之前以中心化机构或可信第三方为核心的交易方式,逐渐转化为端对端去中心化的交易。但在金融、知识产权和医疗等对数据有较强的隐私性的领域,传统区块链公开透明的特性不太能够较好应用。因此本文将零知识证明方法与同态加密过程运用于交易过程,根据交易前后账户变动和资金输入输出情况,产生围绕交易金额的相等性证明和范围证明,使交易在被验证的同时对交易内容进行加密,能够适用于交易数据需要进行隐私保护的场景。1.4 IPFS系统
2 系统方案
2.1 方案模型
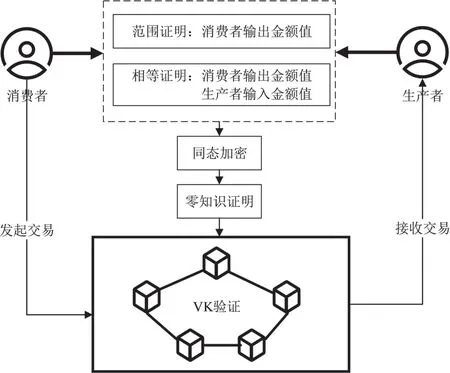
2.2 方案描述
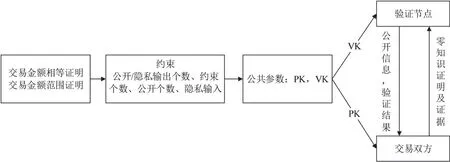
3 方案实现
3.1 算法设计
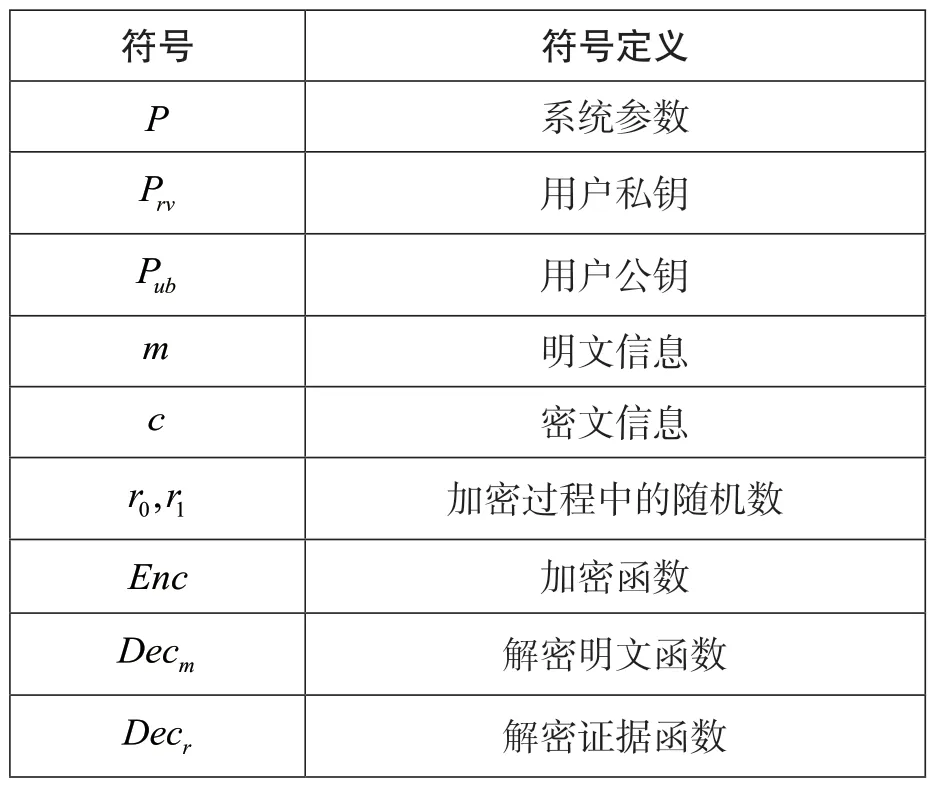
3.2 零知识证明验证
3.3 数据上链交易方案设计
3.4 数据协同设计

4 安全性分析
5 实验分析
5.1 功能性测试
5.2 效率测试
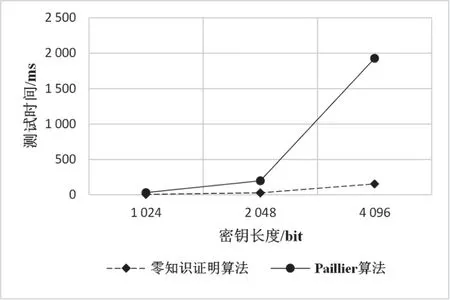
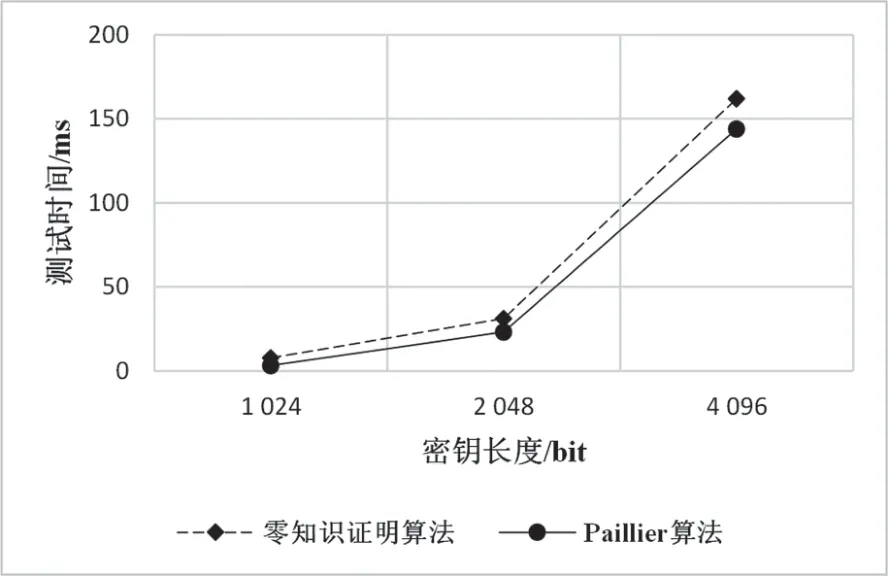
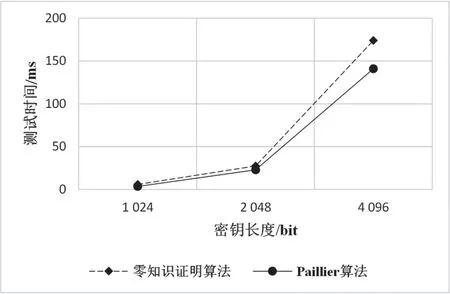
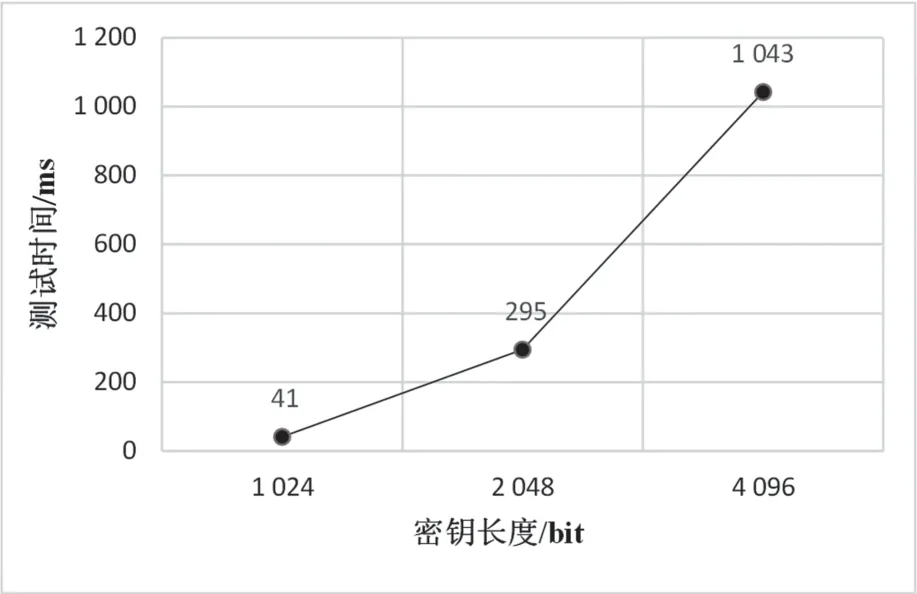
6 结语
