自适应量化权重用于通信高效联邦学习

周治威,刘为凯,钟小颖

(武汉工程大学数理学院,湖北武汉 430205)

1 引言

在过去的几十年里,机器学习兴起,产生了许多与之相关的实际应用,例如机器人、图像识别、机器翻译等等.这些现实应用的开发在很大程度上依赖大数据嵌入的知识,机器学习模型训练需要大量的数据.传统的模型训练依靠大量的移动设备收集数据,然后将数据传输到一个云服务器进行统一训练.这种训练模式不仅要消耗大量的带宽,还存在隐私泄露的风险[1].

基于以上考虑,未来的机器学习任务尽可能在网络边缘(即设备),以分布式方式执行的模型共享训练,称为联邦学习(federated learning,FL)[2-4].在提出的联邦学习算法中有个经典联邦平均算法(federated averaging algorithm,FedAvg)[5],在这个算法中,客户端使用本地数据集更新局部模型,然后将更新好的模型参数上传到服务器,服务器聚集所有客户端的模型参数,更新全局模型,再将全局模型参数广播回所有客户端.重复执行上述步骤若干次或者达到一定的精度为止[1].这种训练模式由于数据存储在客户端本地,不用和其他设备共享数据,减少了隐私泄露的风险.同时FL也为数据孤岛提供了新的思路.然而,FL在训练的过程中会产生巨大的通信开销,在高层的神经网络模型[6]中尤其严重,关于神经网络的稳定可参考文献[7],到现在,通信延迟已经成为了加速FL训练的瓶颈.

在这种背景下,各种通信高效的FL算法开始兴起[5,8].研究人员研究出了大量通信高效的FL算法,介绍如下.文献[9]提出梯度量化加速并行式分布学习,文献[10]提出了梯度稀疏化,文献[11-14]提出了梯度量化来减小模型的尺寸,文献[15]使用梯度差量化,使用误差补偿降低压缩损失[16-17],梯度累积是将多次迭代的小梯度累加再上传[18],文献[19]做了自适应梯度量化,文献[20]证明了自适应线性收敛.在文献[21-22]使用通信审查减少通信传输的比特数,与稀疏化和量化算法不同是,只有当客户端的最新梯度达到设定的阈值才会上传.文献[23]使用了三元权重压缩的方法,在上游通信压缩取得了不错的效果,但是在下游通信压缩的时候有时会发生模型崩溃,引起较大的误差.文献[24]使用压缩感知重建信号,甚至使用1 比特传输数据.神经网络修剪是文献[25]中提出的模型压缩的早期方法.文献[4]做了进一步研究,令人吃惊的是,即使模型压缩了90%,模型依然保持着很高的准确率,联邦学习在实际应用场景中可能会遭受到模型攻击[26-27].联邦学习比较全面的综述可参考文献[28],联邦学习设计理念以及未来的研究方向可参考文献[3,29].

上述方法虽然压缩了数据减少了传输的比特数,但是同时也引入了噪声[30],压缩算法不能收敛到最优解附近,导致算法性能下降幅度比较大.文献[19]中的自适应算法收敛结果比较好,但是所提出算法需要时时通信,保证梯度更新,这消耗了大量的通信资源,现在网络设备计算能力较强,利用增加计算开销,还能更进一步节省通信开销.

受文献[19-20]启发,针对在保证算法性能的情况下,降低通信成本这一问题展开了研究.在联邦平均算法和文献[19]的基础上,本文提出了自适应量化权重算法,该算法能在训练过程中自适应调节量化因子,不断缩小量化误差,压缩数据的同时并保证算法的性能.模型训练达到一定轮次时,会发生不稳定波动,这个时候客户端的每一次更新并非都对全局更新有用[8],为了避免不必要的更新上传,提出了权重复用控制算法,重用上一次的权重更新全局模型,进一步减少上传的比特数,节省通信资源.

本文结构安排如下,第2节介绍FL模型和方法;第3节详细介绍自适应量化权重算法和权重复用控制算法;第4节给出仿真结果和结论;第5节,总结和未来计划.

2 联邦学习模型和常用方法

本节主要介绍经典联邦学习的工作流程,然后介绍自适应量化权重方法的定义和主要特点.

2.1 联邦学习模型

首先联邦学习模型如图1所示,整个模型由1个服务器,n个客户端组成,在正式训练之前,服务器会广播初始模型参数θ0,所有客户端需要下载初始模型参数到本地,然后使用本地数据集训练模型[29],更新局部模型参数(权重),然后将更新好的模型参数上传服务器,服务器聚集所有客户端的局部更新后,进行加权平均更新全局模型参数θ1,再将更新好的全局模型再次广播给客户端,重复上述步骤M次.

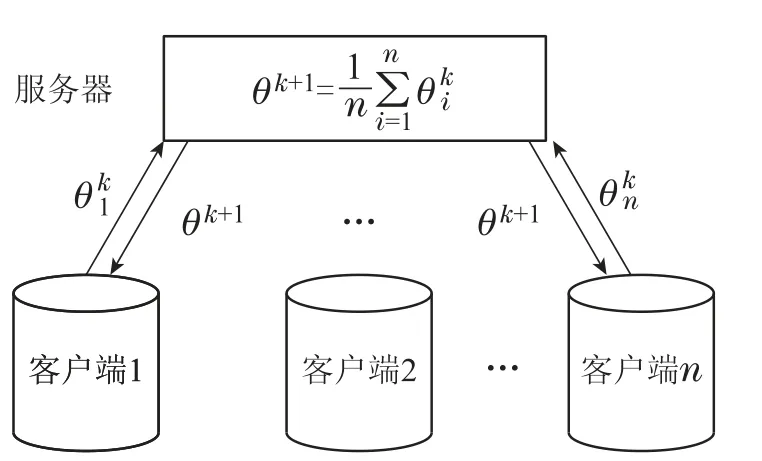
图1 联邦学习模型Fig.1 Federated Learning model

在第k个客户端上的局部损失函数具体如下:

其中:θ是模型参数(权重),假设训练使用的是监督学习,(xi,yi)(i1,2,...,n),x代表数据的输入(图像的像素),y代表模型的期望输出(图像标签),Dk代指客户端本地数据集,k为客户端的编号,L为客户端训练时使用的损失函数.联邦学习的训练目标是构建全局最小损失函数J(θ),全局损失函数定义如下:

其中:N表示客户端的总数,β表示客户端的参与率,不是所有的客户端都能参与训练.客户端都是使用小批量随机梯度下降进行局部模型参数更新,随机梯度下降为

其中:m代表客户端本地迭代轮次,η表示学习率,客户端一般会在本地进行1-10次迭代更新,然后将更新好的模型参数上传服务器,服务器进行加权平均更新全局模型参数,加权更新方式具体如下:

2.2 量化

量化作为数据压缩最常用的手段,通过对矢量的位数加以限制,减少通信过程中传输的比特数[31].现在的许多计算机都使用32或者64位全精度数据进行运算,使用全精度数据虽然准确率高,但是消耗的通信资源非常大.为了缓解这个问题,设计了b位自适应量化器[20].将32位全精度数据量化为b位,通过对全精度数据进行压缩,减少传输的比特数,节省通信资源.

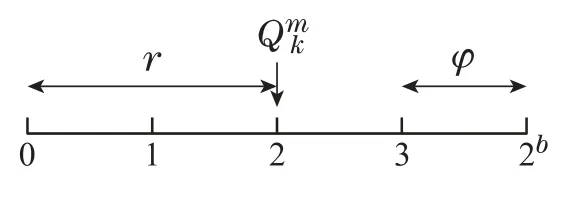
图2 b等于2的量化器Fig.2 b equals 2 quantizer

2.3 提出的算法

在本节中首先提出了自适应量化算法,并在此算法的基础上提出了权重复用控制算法[4,8],前者压缩传输的比特数,后着减少了上传的比特数.算法1总结了自适应量化更新的规则,压缩了传输数据的位数,同时在迭代过程中,自适应调整量化因子,保证了算法的性能.

算法2总结了客户端在更新完局部模型参数之后,对模型参数压缩的过程.算法1总结了训练的全部过程,在每一轮全局更新中,客户端负责用本地数据集更新局部模型参数,然后将更新好的局部模型压缩上传到服务器,服务器负责聚合客户端的局部模型参数,更新全局模型参数,然后将更新好的全局模型参数广播给所有客户端.

在实验过程中发现,随着模型精度达到一定数值之后,模型会出现不稳定的波动,部分客户端上传的模型参数对全局模型更新没有太大的帮助,这时候笔者决定阻止这些不必要的更新上传,直接重用上一次上传的模型参数.判断客户端是否上传的依据是客户端损失值[32].用当前客户端的损失值与上一轮的损失值作比较,比上一次小就上传,并把本次损失值替换上一次的损失值.作为下一轮比较的依据,否则就直接告诉服务器值为空,服务器直接复用上一次上传的权重.服务器需要多耗费一部分空间来存储客户端上传的权重,具体的更新规则总结在算法3中.

3 仿真结果与结论

本节中评估了所提出算法的性能.本文设置了多个实验,比较本文提出的算法在测试精度和通信成本方面的性能.下面介绍实验设置和结果.

3.1 实验设置

为了评估所提出的自适应量化和权重复用控制算法在联邦学习系统中的性能,一台笔记本电脑充当中央服务器和10个通过局域网无线连接的笔记本充当客户[29],假设客户端不会对整个模型发起攻击,也没有外部病毒恶意攻击客户端,详细配置如下.

3.1.1 比较的算法

1) baseline a: 集中式算法,所有数据集中到一台计算机上进行训练,使用随机梯度下降进行训练.

2) baseline b: 标准联邦学习算法[2],没有对模型参数进行过处理,使用的是全精度模型参数进行训练.

3) A-FVG:本文提出的自适应量化联邦学习算法,对客户端的上传的局部模型参数进行量化.

4) WA-FVG:加了权重复用控制的自适应量化算法,在对模型参数进行压缩前进行判断,是否要进行量化上传.

3.1.2 模型

为了评估算法的有效性,选择了3个深度神经网络进行仿真实验(MLP,CNN,CNN5).

1) MLP:该模型包含两个隐层,神经元数量分别为30个和20个,无偏置,选择ReLU作为激活函数.第一层和最后一层的大小分别是784和10.

2) CNN:该模型是个浅层卷积神经网络,由两个卷积层和两个全连层组成,卷积核大小为5×5.使用ReLU函数激活,每个卷积层后加了一个最大池化层,经过两个卷积层后进行dropout策略,dropout参数设置为0.5,第一层神经元320个,最后一层神经元为10个.

3) CNN5: 该模型是一个卷积神经网络,由5个卷积层和2个全连接层组成.第1个卷积层使用ReLU 函数,其余的卷积层后面是批处理规范化层、ReLU函数和最大池化层,全连接层第一层4096 个神经元,第二层10个神经元.

3.1.3 数据

本文选择使用标准检测数据集MINST[25]和CIFAR10[10]做仿真.

1) MNIST:它包含60 000个用于训练和10 000个用于测试的10类灰度手写图像样本,其中每幅图像的维数为28×28.所有数据都是独立同分布的数据.

2) CIFAR10: 它包含了猫、狗、飞机等10种物体的60000个彩色RGB图像,其中每幅图像的维数为32×32,50000个用于训练,10000个用于测试,数据类型属于非独立同分布数据.

3.1.4 其他配置

客户端总数N设置了10个,客户端本地循环次数E设置为5,迭代总轮次M设置为500,客户端参与率设置为1,数据的批处理大小设置为64,学习率设置为0.01.

3.2 仿真结果分析

对于客户端的数据来源,因为客户端的数据应该是独立的,所以本文把下载的数据集平分给所有的客户端.以cifar10数据集为例,每个客户端可以分到6000个数据,在全局模型聚合后用10000个测试数据测试模型的学习效果,表1展示了4种算法在mnist数据集上的测试结果.本文比较了算法达到稳定后,标准联邦平均算法baseline b,自适应量化算法A-FVG和权重复用控制算法WA-FVG所需要的通信成本,本文将客户端模型参数做6位量化处理.

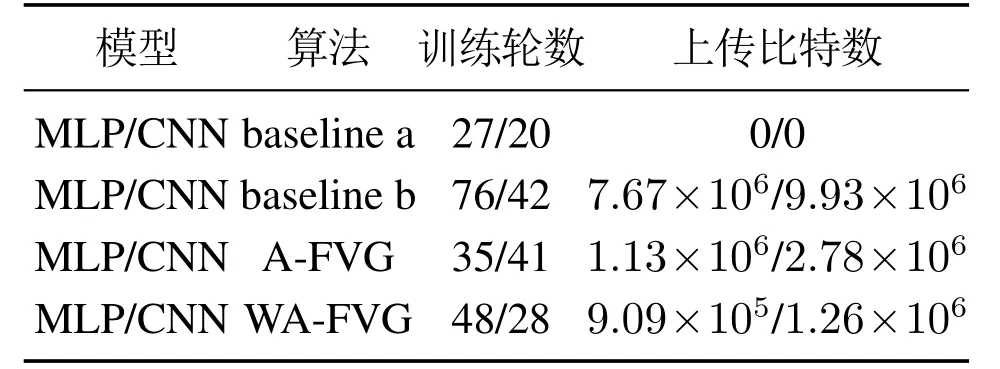
表1 Mnist数据集测试结果Table 1 Mnist data set test results

图3是4种算法在mnist数据集上的通信轮次对比图,从中可以看出A-FVG和WA-FVG两种算法的收敛速度比标准联邦学习算法的收敛速度更快.集中式学习算法达到了0.962准确度,标准联邦学习算法达到了0.940,本文的A-FVG和WA-FVG算法准确度分别达到了0.941和0.927.A-FVG和标准联邦学习算法基本达到了一样的精度,但是本文的WA-FVG算法相比A-FVG算法有大约1.4%精度损失,笔者推测是本文使用平均损失值作为是否复用的依据引起的.在客户端进行多次局部迭代时,可能有某次迭代对于全局模型更新是有用的,但是因为其他几次的迭代更新对全局更新无用,从而导致将有用的更新平均掉了,没有上传.但是从图3中算法达到收敛需要上传的比特数对比图可以看出,本文的权重复用算法相比经典联邦算法要节省大概75%～80%的通信资源,A-FVG相比经典联邦学习算法要节约70%的通信资源.

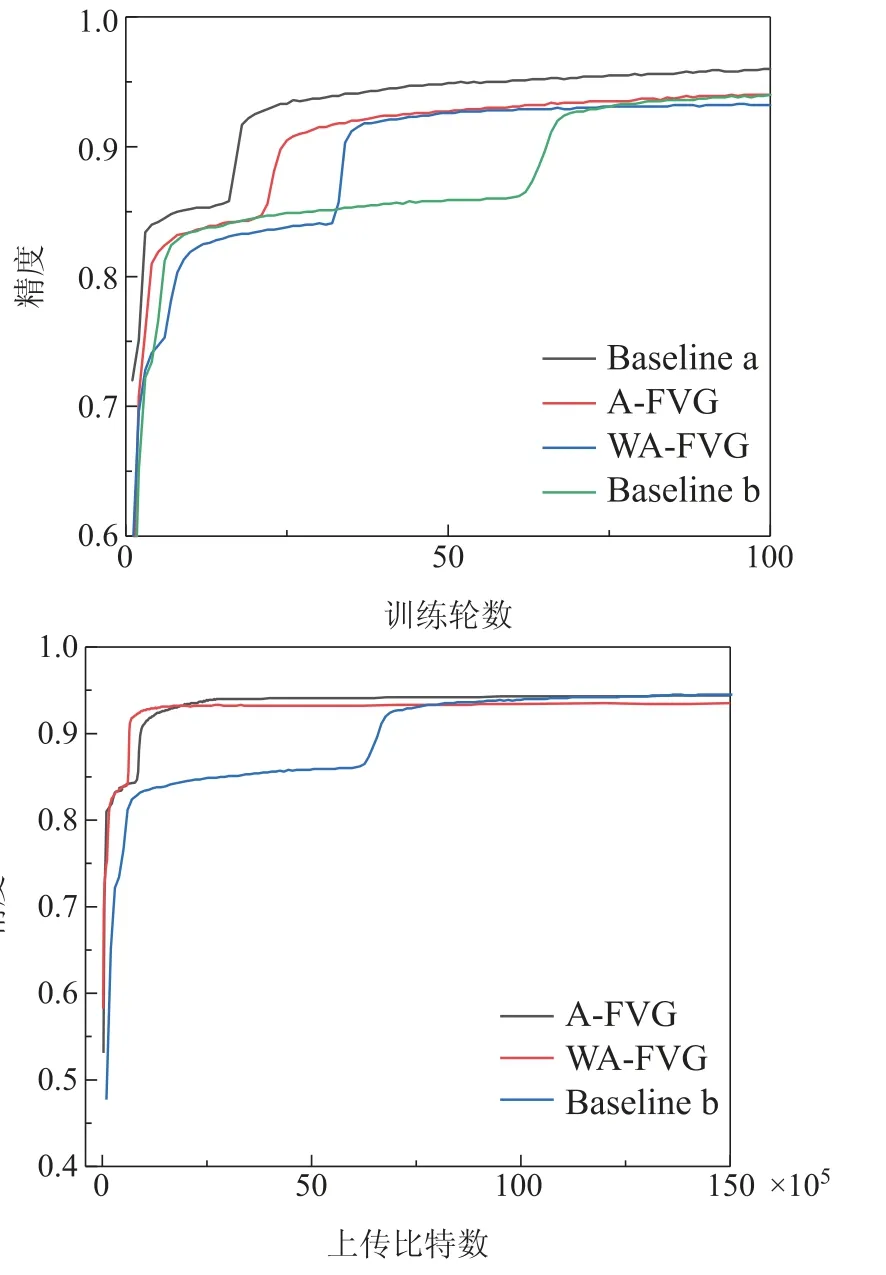
图3 Mnist数据集MLP网络通信成本Fig.3 Mnist dataset MLP network communication cost

在CNN网络中,集中式和标准联邦学习算法准确度分别达到了0.990,0.986.A-FVG和WA-FVG 算法分别达到了0.986,0.982.4种算法都到了惊人的准确度.从图4的通信轮数对比图看不出优势,但是从图4达到收敛需要上传比特数对比图可以看出,本文的算法还是很有效,节约了70%以上的通信资源的同时没有引起太大的性能下降.

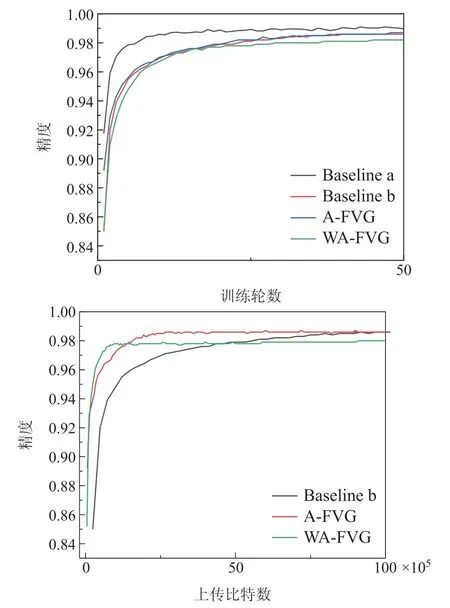
图4 Mnist数据集CNN网络通信成本Fig.4 Mnist dataset CNN network communication cost

为了证明本文算法的稳定性,在非独立同分布数据集上也进行了同样的实验.只是在非独立同分布数据集上(Cifar10)进行联邦学习性能下降仍然是个巨大的挑战[33],因为当数据是非独立同分布的时候,局部随机梯度不能被认为是全局梯度的无偏估计[34].为了提高识别的准确度,本文选择CNN和CNN5这两个更为复杂的模型进行实验,实验参数不变.

表2展示了4种算法在Cifar10数据集上达到稳定所需要的训练轮数和上传的比特数,图5为CNN网络实验结果,在CNN网络中集中式算法准确度能达到0.617,标准联邦学习与A-FVG算法能达到0.594和0.592,准确度几乎一样,说明本文自适应量化是有效的,WA-FVG算法能达到0.586,与A-FVG相比只降低了不到1%的性能,4种算法的收敛速度在CNN网络中几乎一样,但是WA-FVG 算法比A-FVG算法节省了5%～10%的通信资源,比标准联邦平均算法减少了75%以上的通信资源.

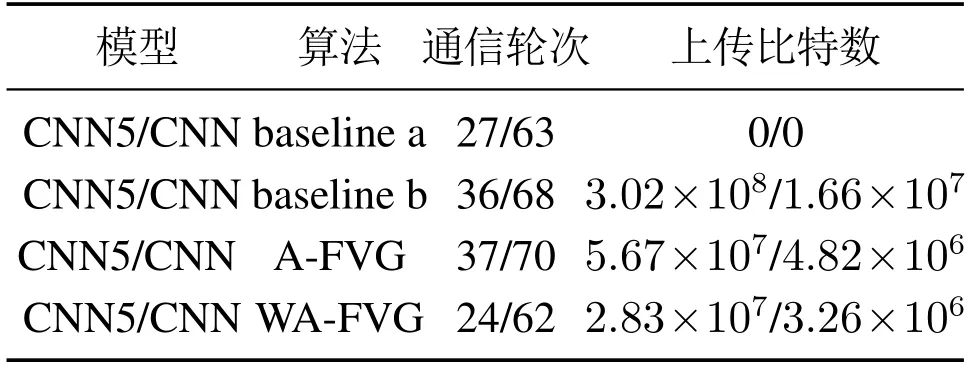
表2 Cifar10数据集测试结果Table 2 Cifar10 dataset test results

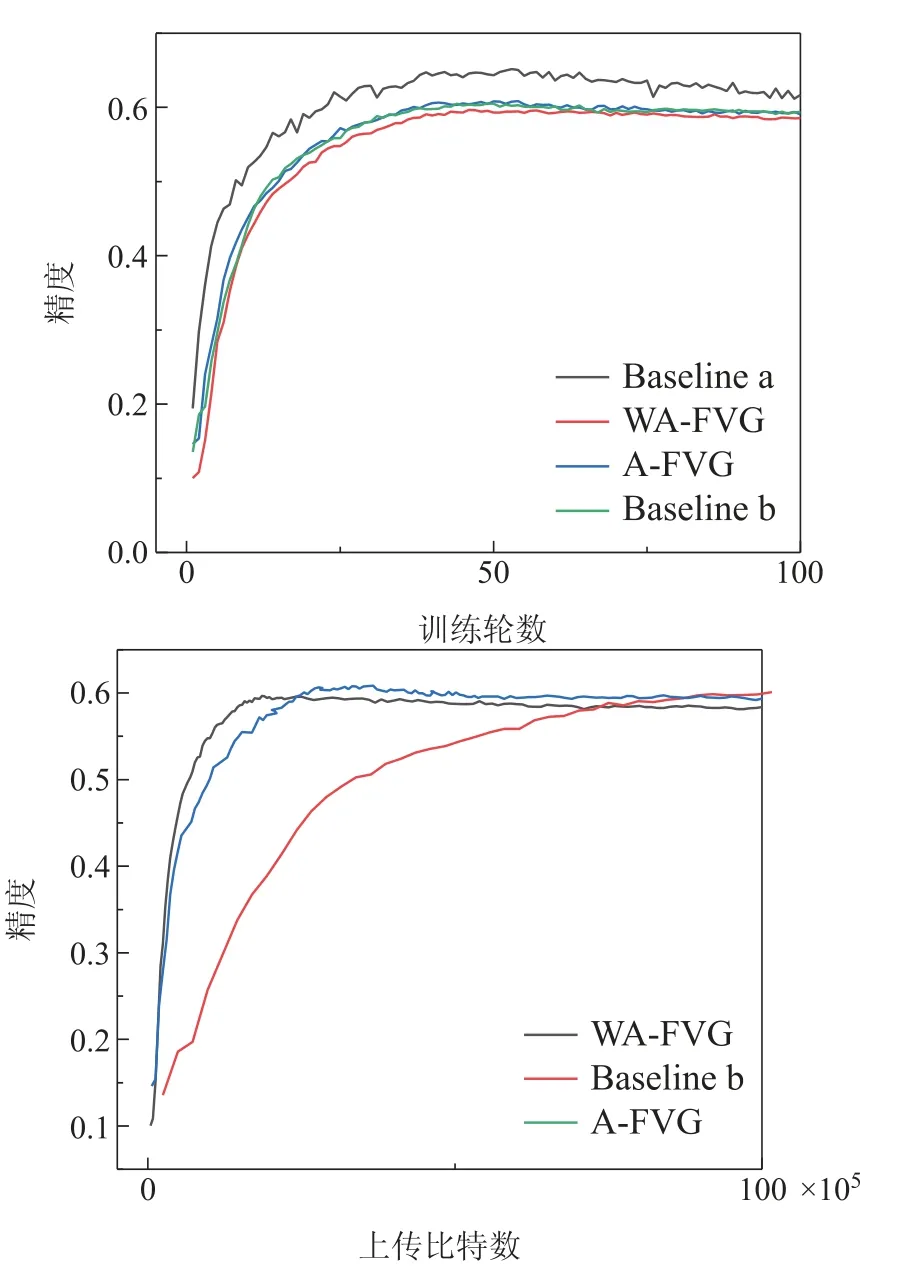
图5 Cifar10数据集CNN网络通信成本Fig.5 Cifar10 dataset CNN network communication cost

图6展示了更为复杂的CNN5网络实验结果,集中式算法准确度能达到0.785,标准联邦学习与A-FVG算法分别能达到0.767和0.766,WA-FVG算法达到了0.758,与CNN网络所得到结论几乎一致,这表明了本文的算法在更为复杂的模型上依然能保持很好的稳定性.

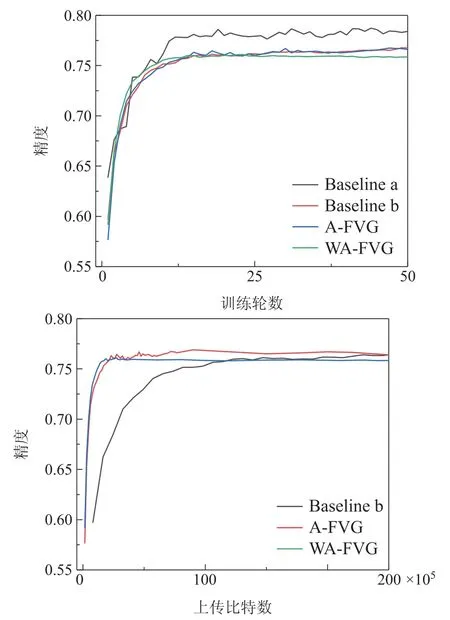
图6 Cifar10数据集CNN5网络通信成本Fig.6 Cifar10 dataset CNN5 network communication cost

3.3 参与率的影响

这一节测试了客户端在不同的参与率下,对AFVG算法精度的影响,这里的参与率指的是客户端参与通信的比例,所有客户端都参与训练,服务器根据参与率随机选择一部分客户端参与通信.

选用MLP网络和Mnist数据集进行实验,其他实验参数不变.从图7通信轮数图可以看出,参与率的改变对模型的最终稳定性没有太大的影响,但是低参与率的情况下,模型的收敛速度反而更快,需要的通信轮次也相应的减少,能减少大量的通信资源,再结合图7在不同的参与率下,需要上传的比特数对比图,从中可以看出,随着参与率越小,算法达到收敛时需要上传的比特数也在减少,这个结果非常的令人振奋,因为在实际的环境中,客户端的基数非常庞大,如果使用较低的参与率就能达到一个满意的效果,那么可以减少大量的通信资源.

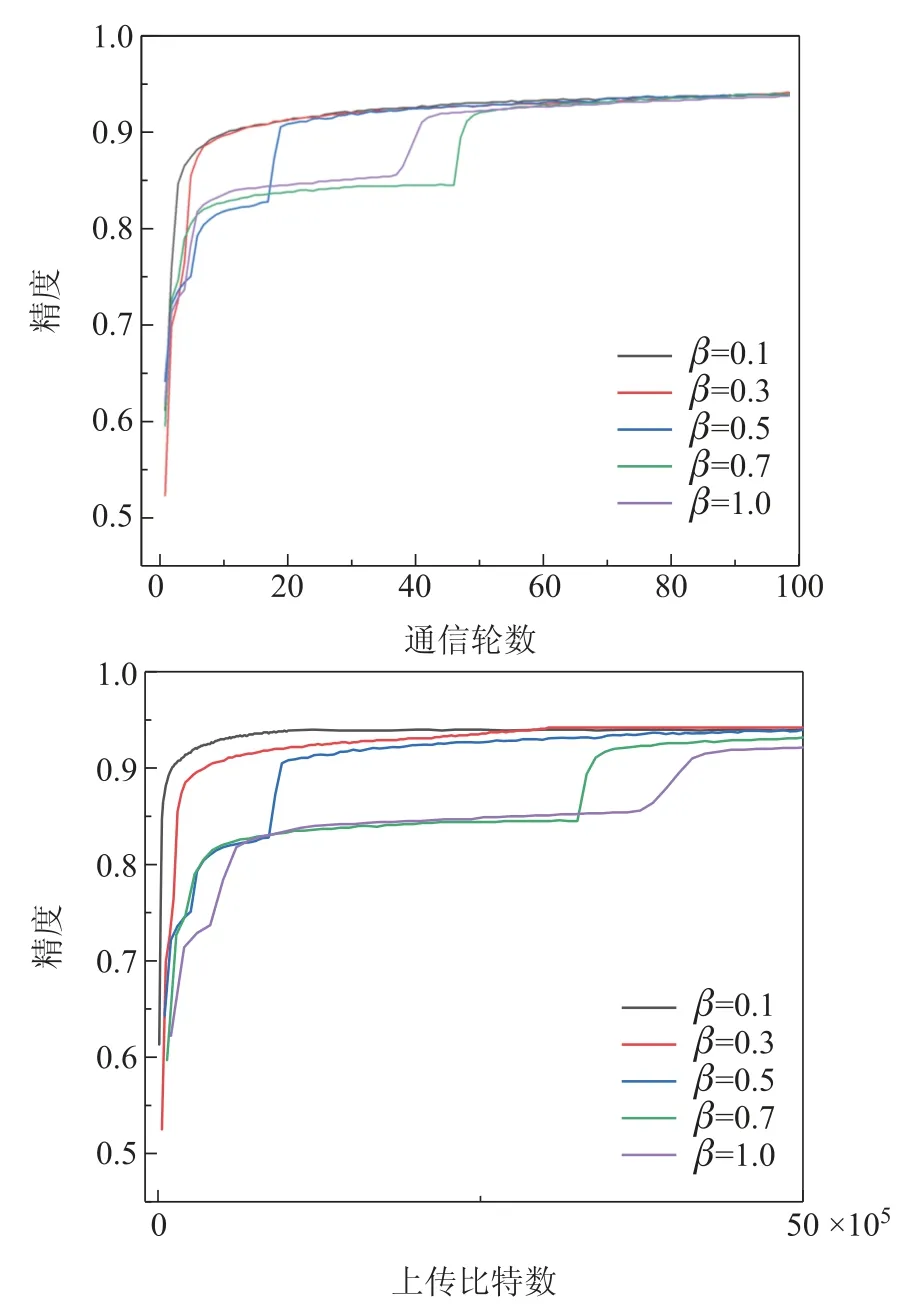
图7 参与率通信成本Fig.7 Participation rate communication cost

3.4 量化位数的影响

在这一节研究了量化位数b对A-FVG算法精度的影响,其他实验参数不变,依然使用MLP网络和Mnist数据集.

图8的通信轮数对比图显示了A-FVG在不同量化位数b下所能达到的精度以及需要的通信轮数,可以看出,除了使用2位量化会导致性能下降比较大以外,其他量化位数对最后的准确度影响比较小,但是在通信轮数上的结果很明显,使用6位量化收敛速度最快.使用的量化位数越少,收敛的反而更快一些.再结合图8不同量化位数下需要上传比特数对比图,可以看出使用的量化位数越少,算法达到收敛时需要传输的比特数也更少.这个结果很让人高兴的,在现实环境中,数据量非常庞大,如果使用低位量化也能得到比较好的结果,那么就可以节省大量的通信资源,降低通信成本.

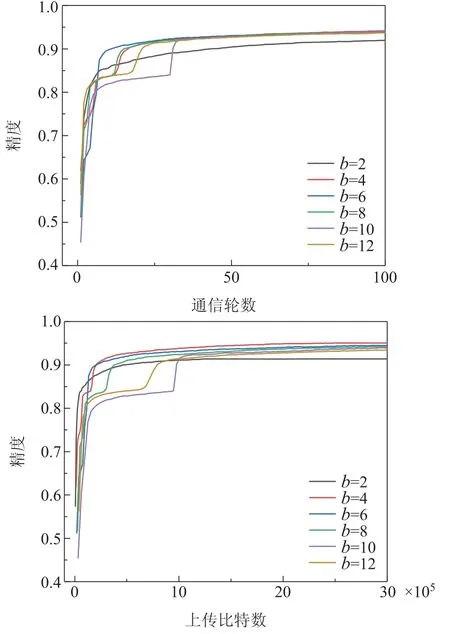
图8 量化位数通信成本Fig.8 Quantify the cost of bit communication

4 结论和未来的工作

本文针对联邦学习训练过程中通信资源有限的问题,提出了自适应量化权重算法和权重复用控制算法,自适应量化算法在迭代过程中,能自适应调节量化因子,从而使得量化后的权重与真实权重之间的误差越来越小.通过仿真实验表明,本文提出的算法有效,在没有引起性能大幅度下降的同时,压缩了传输的比特数,降低了70%以上的通信成本.权重复用算法根据客户端损失函数的损失值来判断是否上传,因为控制方式的原因,导致会引起1%～2%的性能下降,但是能减少75%～80%的通信成本,在未来工作中计划找出一种更有效的控制策略,并且为算法的性能提供更多的理论论证.