基于分布式深度强化学习的微电网实时优化调度

郭方洪,何 通,吴 祥,董 辉,刘 冰

(浙江工业大学信息工程学院,浙江杭州 310034)

1 引言

为落实2030年“碳达峰”和2060年“碳中和”目标,国家提出要构建以新能源为主体的新型电力系统[1].微电网(microgrid,MG),作为新型电力系统的典型代表,其内部包含分布式供电单元、储能单元和负载单元.微电网运行可以分为孤岛与并网两种模式[2].在并网模式下,微电网通过闭合公共耦合点上的隔离开关连接主电网.相比于孤岛模式,微电网通过与主电网进行电能交易,可以有效提高系统稳定性[3].然而,相对于传统的大型电网,微电网并网引入了多种新能源,其能量管理存在着不确定性强的问题.

针对含不确定新能源出力的微电网优化调度问题,目前常用的求解方法主要包括动态规划[4]、随机线性规划[5]、微分进化算法[6]和飞蛾扑火算法[7]等数值优化方法.此外,文献[8-9]提出使用机会约束规划算法对风光储系统以及风火储系统进行优化求解.上述方法虽然可以有效解决特定场景下的优化调度问题,但是由于微电网系统负载的实时波动性,常规的数值优化方法难以胜任其高效的实时优化调度要求.鉴于强化学习可以根据模型快速对实时变化的环境做出反馈,其被广泛应用于求解实时性优化问题的领域.例如,文献[10]利用了深度Q学习(deep Q network,DQN)算法实现了配电网电压控制优化,文献[11]提出了双深度期望Q网络(double deep expected Q network,DDEQN)算法,借助贝叶斯神经网络对强化学习中不确定的学习环境建模,优化DNQ算法中Q值的迭代规则来求解微电网随机经济调度问题.值得指出的是,上述基于集中式框架的强化学习方法通常只能适用于规模有限的微电网系统.随着新能源大规模接入电网,系统模型中可控发电单元数量、模型的动作、状态空间成倍增长,微电网优化调度面临计算复杂度高等问题,集中式强化学习算法可能不再适用.受分布式优化技术在微电网优化调度应用上的启发[12-13],本文拟设计一种分布式深度强化学习方法来解决上述微电网优化调度中遇到的诸如不确定性强、实时性要求高、参数空间大等问题.

区别于文献[14-19]中的传统强化学习使用中心化训练、执行的思想,本文结合文献[20-21]中的分布式深度神经网络结构和分布式Q学习方法,提出了一种基于分布式深度强化学习的微电网实时优化调度策略.首先,视各个分布式电源为独立的智能体,建立多智能体深度强化学习模型;其次,将每个分布式电源以及主电网的优化调度设计为多目标优化问题.其主要目标是: 最小化发电单元的发电成本,优化微电网系统与主电网的电力交易,以及降低发电单元与储能单元的使用寿命损耗.各个智能体通过相互交互,从而实现全局最优.与传统的强化学习方法相比,本文所提的分布式深度强化学习方法解决微电网优化调度问题具有如下优势: 1)采用深度强化学习模型,提高了微电网系统的实时优化调度能力;2)为每个智能体建立相应的本地学习模型,有效地降低了计算复杂度;3)优化智能体动作设计,提高了微电网系统优化调度的精度.

本文剩余章节组织如下: 第2节建立了基于分布式框架的微电网模型;在第3节中,基于模型的分布式特点,提出了一种基于分布式深度强化学习的微电网实时优化调度策略;第4节对具体的应用场景进行了算法仿真测试,并与传统深度强化学习算法进行对比,验证了所提方法的优越性;最后第5节对文章进行总结.

2 问题描述与模型构建

2.1 微电网能量优化调度

微电网能量优化调度的主要目标是在满足各项约束的前提下,各分布式电源相互交互、更新模型策略、调节本地输出功率,从而降低运行成本,提高系统经济性.

本文考虑的微电网系统(如图1所示)包括n个独立发电单元,m个负载,实时充放电的储能单元以及可以进行电力交易的主电网.第i个发电单元在t时刻的发电功率记为PG,i(t),第j个负载在t时刻负载需求为Pd,j(t).储能单元在t时刻的荷电状态为SoC(t),充放电功率为Pess(t),当发电单元的发电量超出或者低于负载需求时,储能单元会存储或输出功率来维持系统供需平衡.微电网与主电网的交换功率为Pgrid(t),当微电网从主电网获取电力时,Pgird(t)为正,输出电力时则为负.

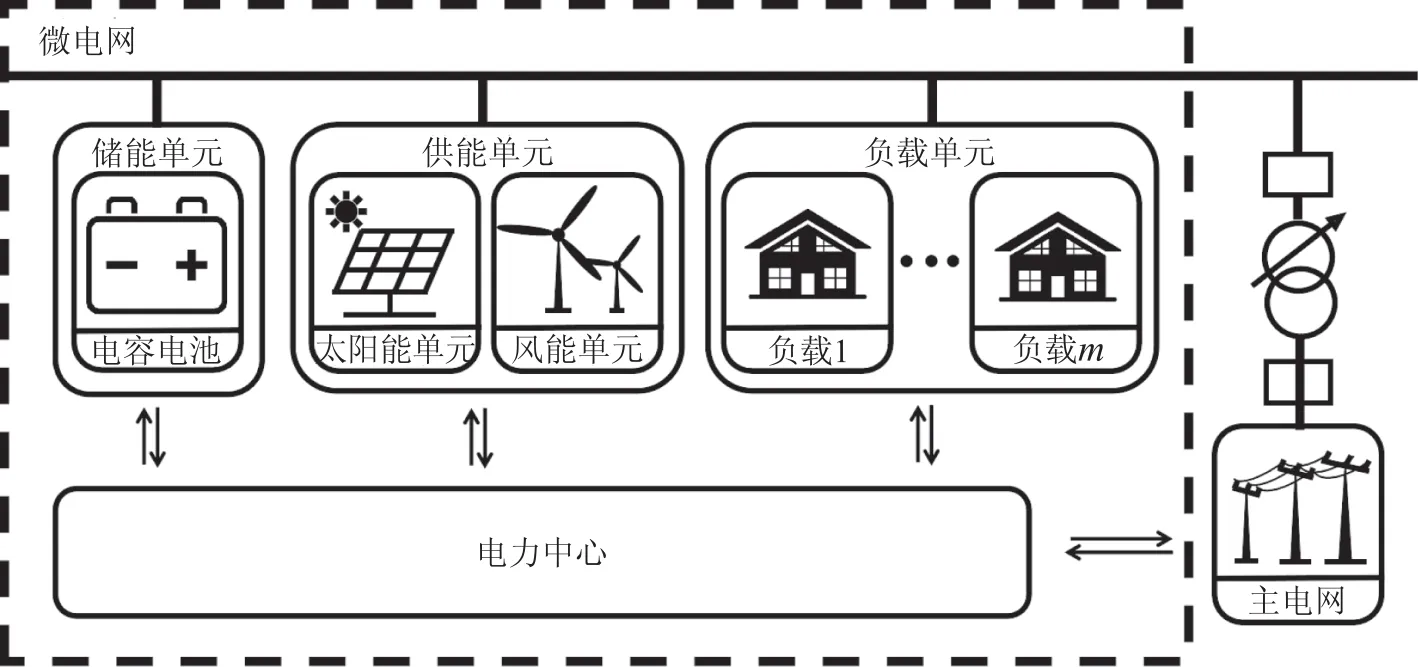
图1 微电网模型Fig.1 Microgrid model

2.2 代价函数

考虑到系统发电成本以及寿命,本文将主要优化目标分为4个部分:

1) 在满足负载需求以及确保功率平衡的条件下,尽可能降低发电单元的发电成本,使微电网系统运行成本最低[20].发电成本代价函数表示为

其中αi,βi,γi为第i个发电单元发电成本系数.

2) 优化发电单元之间的电力调度,使发电单元尽可能工作在最优点,从而降低发电单元的使用损耗.控制储能单元的充放电行为和强度,防止系统高强度地使用储能单元导致储能单元使用寿命下降.发电单元与储能单元使用寿命的代价函数表示为

其中:Popt,i为发电单元最优工作功率,为储能单元最大使用寿命.

3) 为防止过负载情况的产生,储能单元荷电状态需保持在理想状态.储能单元荷电状态代价函数表示为

其中SoC(t)为储能单元在t时刻的荷电状态,其方程可以表示为

其中:SoCopt为理想荷电状态,ESSscp为储能单元的储能容量.

4) 考虑到电价随时间段分为峰平谷3个价位,微电网系统需要在满足约束的前提下,降低与主电网的交易成本.其代价函数表示为

其中Pricelevel(t)为t时刻的电价.

最终,本文建立的多目标优化调度问题的代价函数可表示为

其中θ1,θ2,θ3,θ4为各优化目标对应的权重.

2.3 约束条件

1) 功率平衡约束: 在t时刻,微电网的功率平衡约束可以表示为

2) 爬坡约束: 由于发电单元功率变化幅度有限,同时为了避免储能单元过度的充放电造成损耗,因此储能单元在单位时间内,充放电功率被限制在一定范围内.爬坡约束表示为

其中: CLmax,i,CLmin,i分别为发电单元爬坡功率上下限;CLess,max,CLess,min分别为储能单元爬坡功率上下限.

3) 功率上下限约束: 微电网中,每个发电单元都存在发电功率上下限.微电网从主电网交易的电量也受到传输线最大功率限制的约束.功率上下限约束表示为

其中:Pmax,i,Pmin,i分别为发电单元出力功率上下限,Pgridmax,Pgridmin分别为主电网交换功率上下限.

4) 储能单元荷电状态约束: 为了保证储能单元的持续稳定运行,需要将荷电状态限制在一定范围.储能单元荷电状态约束表示为

其中: SoCmax,SoCmin分别为储能单元荷电状态上下限.

2.4 微电网能量优化调度问题

综上所述,结合能量优化调度目标(6),同时考虑约束条件(7)-(12),微电网优化调度问题可以表示为P1.

其中T为管理优化周期.基于上述目标,考虑到系统运行时发电单元和负载的实时性与波动性等特点,为此,本文以深度强化学习算法为基础,并根据微电网中可控单元数量多的特点,提出了一种基于分布式深度强化学习的微电网实时优化调度方法.该方法提高了微电网系统实时优化调度能力,结合分布式框架优化了多智能体环境下复杂的参数空间,从而降低了计算复杂度,加快了优化调度响应速度.

3 基于分布式深度强化学习的微电网实时优化调度方法

3.1 MADDPG算法原理

本文基于DDPG算法进行设计,结合了基于Q值的价值网络(critic network)与基于动作选择的动作网络(actor network),可以解决连续动作区间上的动作筛选问题[22].传统的强化学习方法在解决单智能体问题时都能取得较好的学习效果,但当面对多智能体相互合作或竞争的环境时,由于状态与动作空间随着智能体的增加而成倍增长,因此模型无法有效学习.为了克服这一难题,本文采用多智能体深度强化学习算法(multi-agent deep deterministic policy gradient,MADDPG).

不同于传统的强化学习中心化训练与执行的思想,MADDPG以集中式训练、分布式执行为主要思想,不再以一个中央决策智能体为整个系统的决策核心,而是为每个智能体构建一个负责本地决策的深度神经网络,既而采用基于价值网络和动作网络的DDPG算法为其行为决策.在训练过程中,每个智能体都可以获得所有智能体的状态和动作信息,学习动作策略,通过调整自身输出功率,来更好地优化本地的价值网络.

3.2 神经网络设计

神经网络由估计网络与现实网络组成,因此MADDPG算法为每个智能体建立了基于动作选择的动作估计网络和基于价值的状态估计网络以及相应的现实网络.由于数据之间存在时间耦合性,估计网络与现实网络需要分别采用实时参数和历史参数来构建,动作估计网络和状态估计网络的参数分别为θµ,θQ,动作现实网络和状态现实网络的参数分别为根据图1的微电网模型,这里本文共设定n+1个智能体,其状态集合为S{s1,s2,...,sn+1};动作集合为A{a1,a2,...,an+1};动作策略集合为π{π1,π2,...,πn+1};奖励集合为R{r1,r2,...,rn+1}.在t时刻,每个智能体的状态值和动作值设定如下所示:

状态变量设计时,需要能使智能体寻求满足约束的可行解,因此本文根据所得解是否满足约束,将奖励值计算设计成两种模式: 当解满足约束时,根据式(6)计算出整体的成本函数,将其相反数作为奖励值供模型学习;当解不满足约束时,则直接给奖励值赋予一个绝对值极大的负数作为惩罚,算法具体更新流程如图2所示.每个智能体设置一个经验池,在训练神经网络时随机从经验池中抽取历史数据来学习,数据存储模式为(S,S＇,A,R),S＇为下一时刻的状态变量,神经网络更新流程如图3所示.

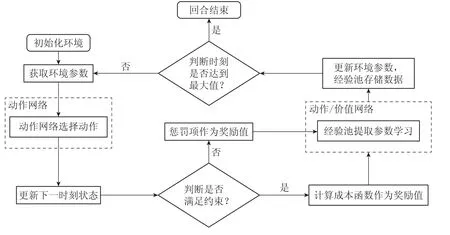
图2 算法更新流程图Fig.2 Algorithm update flowchart

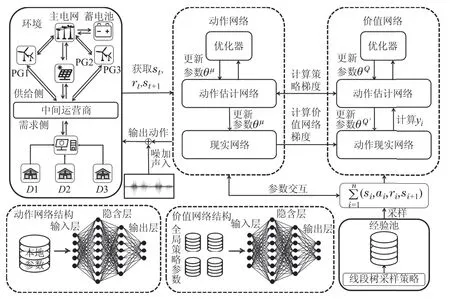
图3 智能体神经网络更新流程图Fig.3 Agent neural network update flowchart

1) 价值网络.

MADDPG算法与其他深度强化学习算法相比,最大的特点在于其价值网络的设定.传统的深度强化学习算法建立价值网络的主要作用是通过与环境的交互,掌握奖惩信息与环境的关系,为动作网络做出的动作进行评判使其寻求更高的奖励.而MADDPG在此基础上,为每个智能体均创建一个价值网络,并且每个价值网络都能得到所有智能体的状态和动作信息,通过学习其他智能体的策略,来更好地优化本地价值网络策略.首先,将n+1个智能体的策略参数用θ[θ1,θ2,...,θn+1]来表示,单个智能体的累计奖励及其策略梯度如下:

其中:ρπ为状态s所服从的分布,πθ为动作策略,为估计网络的状态-动作函数,代表某状态下选取该动作的潜在奖励,用于计算损失函数.exp为从经验池中调出的一组经验数据.价值网络以最小化每个智能体的损失函数值作为更新方向,损失函数计算公式如下:

其中:yi为对应的目标Q值,为现实网络的状态-动作函数,γ为奖励衰减系数.

2) 动作网络.

对于单个智能体而言,其他智能体都是环境的一部分,当动作网络接收所有智能体的策略时会影响环境稳定性,因此每个智能体的动作网络只获取本地的状态数据,并且在价值网络的评判下学习.相比于价值网络基于Q值进行选择,动作网络则根据价值网络给出的评判来修改每个动作被选择的概率,并根据该概率来选择动作.动作网络的累计奖励及其策略梯度如下:

动作网络中的动作现实网络则是从经验池中提取历史数据,并将下一个状态作为输入,选择对应的最优动作作为输出.动作现实网络与状态现实网络其参数迭代均采用如下的软更新方式:

其中τ是一个远小于1的常数,用于减小神经网络参数变化,使其易于收敛.

3.3 参数空间设计

针对本文研究的微电网模型,本节为各个智能体设计了相似的动作空间、状态空间和奖励函数.

1) 动作空间: 本文主要有两类智能体,一类是所有的发电单元,一类是进行电力交易的主电网.传统的做法是将每个发电单元的发电功率PG,i(t)以及与主电网的交换功率Pgrid(t)作为动作空间.然而随着智能体数量增加,当把发电单元的发电功率作为动作时,其较大的取值范围会极大地提高模型学习的难度.因此本文对动作空间进行了简化,将t时刻至t+1时刻发电单元发电功率的变化量ΔPG,i(t)作为动作.主电网的动作为当前时刻的交换功率.储能单元的充放电功率Pess(t)则由功率平衡直接求得,因此不需要为其设置动作空间.

2) 状态空间: 考虑到动作网络在选择动作时,只能基于本地的状态值进行选择,因此本文在发电单元与主电网的状态空间设计上略有不同.对于每个发电单元,本文将当前所在的时刻t、外部电价、储能单元荷电状态以及各发电单元发电功率作为状态,智能体获取的全局状态参数集合表示为

对于主电网,状态空间设计为当前时刻t、外部电价以及主电网与微电网系统的交换功率,智能体获取的全局状态参数表示为

3) 奖励函数: 奖励函数主要分为两部分,一部分为满足约束时成本函数的相反数;一部分为违反约束条件时产生的惩罚.为了避免系统违反约束条件,本文根据式(6)建立如下惩罚项:

其中∊,η为超出约束的惩罚系数,分别为较小与极大的正值.

本方法以深度强化学习为基础,在模型训练完成后,使用训练成熟的神经网络模型对环境变化做出快速反应,实现了微电网实时优化调度.并且使用分布式框架来解决多智能体环境,简化了单个神经网络的模型,极大程度上降低了计算复杂度.

4 仿真实验

本节在Python3.6环境下进行仿真实验来验证所提方法的有效性.在训练阶段,使用系统状态参数组成的训练集对模型进行训练;在测试阶段,采用新的系统状态参数测试学习后的模型性能.本节展示了MADDPG算法在多智能体环境下的各项参数收敛性能,并且与DDPG算法进行了对比实验.本次仿真考虑的微电网模型含有3个分布式发电单元,并设置1个储能单元来配合发电单元工作.发电单元与储能单元的参数如表1所示.

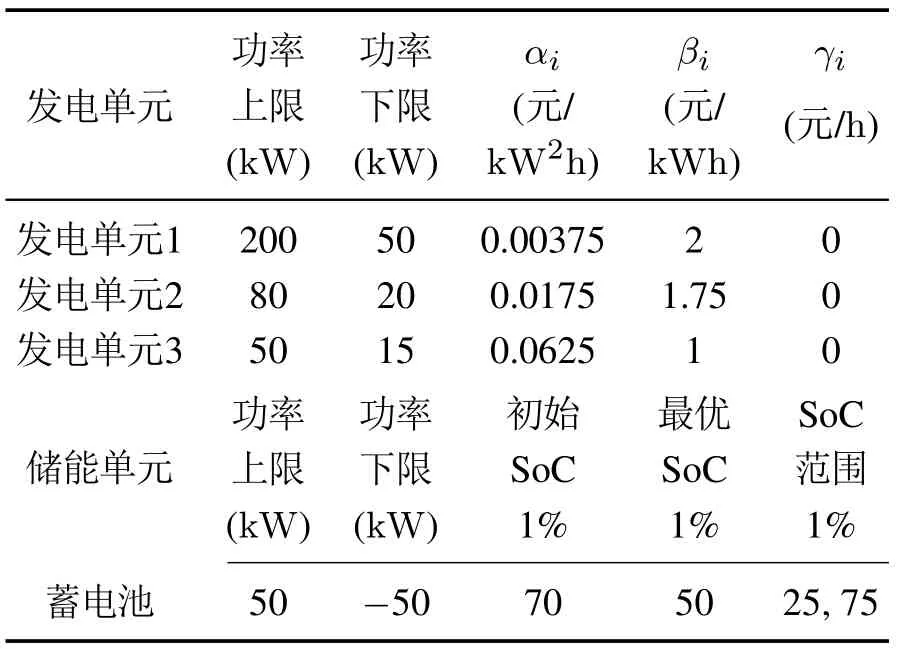
表1 发电单元与储能单元参数Table 1 Parameters of generator and energy storage

在仿真过程中,负载需求随着时间的变化存在较大的差异,当储能单元与发电单元无法满足负载需求时,系统可以从主电网中获取当前时刻差额电量;当储能单元荷电量较高时,也可通过主电网输出多余的电力来产生一定的经济效益.本文将一个管理优化周期分为24个时间段,每个时间段代表1个小时,单位时间内主电网最大交换功率为200 MW.考虑到实际用电时电价根据时间段分为峰平谷3个价位,将主电网实时电价分为4个阶段,如表2所示.

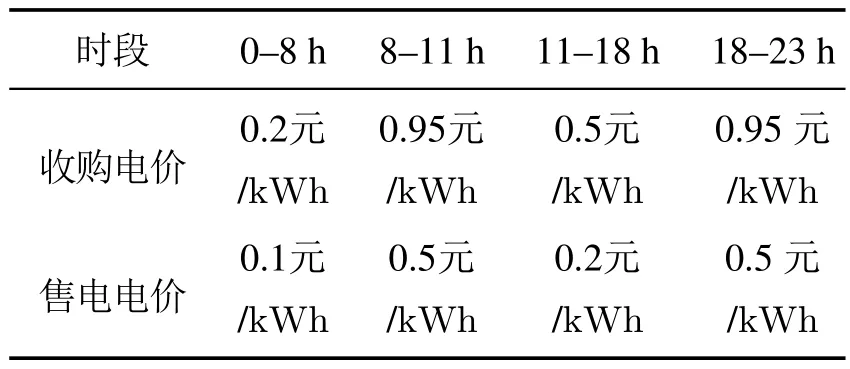
表2 主电网实时电价Table 2 Real-time electricity price of main grid

4.1 MADDPG与DDPG算法对比

根据以上设置,本文首先对分布式深度强化学习算法MADDPG与集中式深度强化学习DDPG算法进行横向比较.神经网络参数如下: 每个神经网络设置64个神经元;动作神经网络与状态神经网络的学习率分别为0.0001和0.001;经验池最大存储100000组数据,每次学习时随机提取32组.两种算法的训练次数均设置为10000,并对每40周期的数据进行一次均值化处理.图4为两种算法在相同条件下的奖励值变化曲线图,其中DDPG算法直接计算整体的奖励值,MADDPG算法只计算每个智能体本地产生的奖励,总奖励值为4个智能体的本地奖励总和.从图中可以看出,在训练初期阶段,由于动作网络均处于动作探索阶段,因此两种算法的奖励值较低,且存在较大波动.随着智能体开始从经验池中提取历史数据进行学习,奖励值逐渐呈现明显上升趋势,当达到2800周期左右时,MADDPG算法的奖励值逐渐收敛于-30000附近,然而DDPG算法使用了3400周期左右逐渐收敛于-90000附近,并且仍然存在较大的波动.显然,本文提出的基于分布式MADDPG的实时优化调度方法获得的系统总奖励要优于集中式的DDPG 算法,且收敛速度更快.

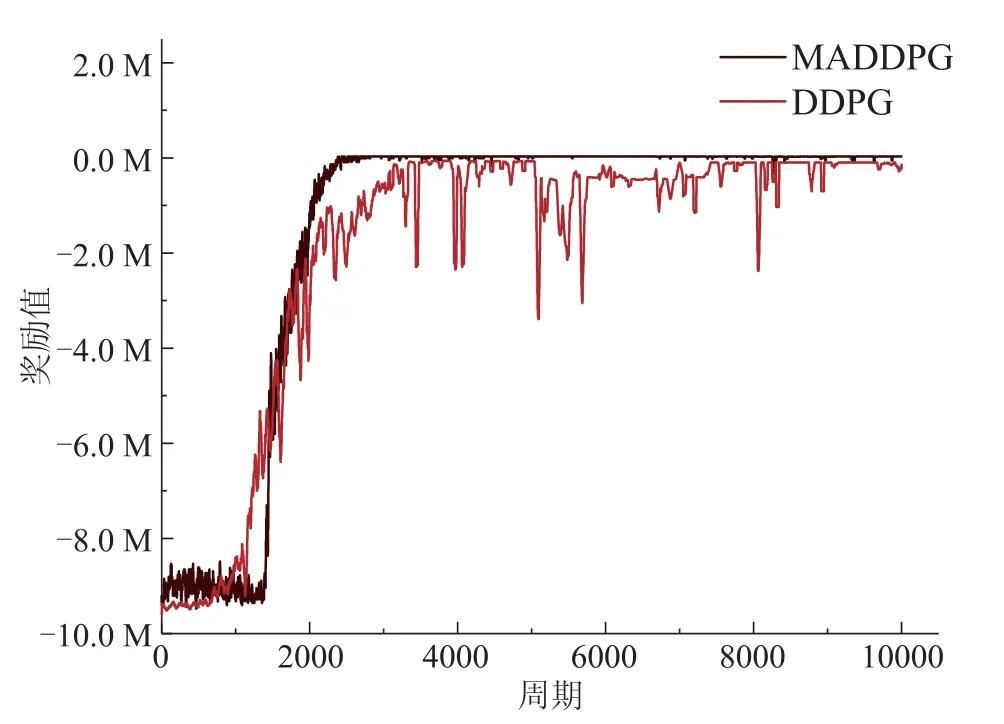
图4 MADDPG与DDPG算法对比图Fig.4 Comparison of MADDPG and DDPG algorithms

4.2 基于MADDPG算法的微电网实时优化调度

考虑到在训练过程中,不同智能体的奖励评判标准不同,本节分别给出3个发电单元与主电网模型训练完成后,单周期内出力功率以及交换功率变化曲线图.发电单元出力功率如图5所示,发电单元1在24 h内发电功率在最优工作点160 kW附近波动;发电单元2在最优工作点60 kW附近波动;发电单元3在最优工作点40 kW附近波动,可见训练过程中每个发电单元的发电功率始终跟踪其最优工作点.主电网交换功率如图6所示,主电网交换功率均为负数,说明在模型训练完成后,模型可以做到在单位周期内,通过本地各发电单元相互调节,使微电网系统在与主电网交易过程中,获得一定的经济效益.结果表明,4个智能体在训练完成后,均能逼近最优代价函数值,从而降低了系统运行成本.

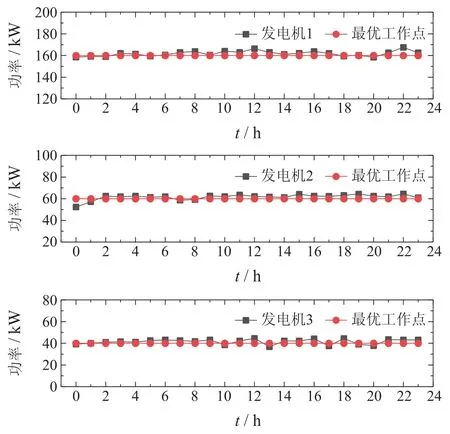
图5 发电单元出力功率Fig.5 Output power of generation units

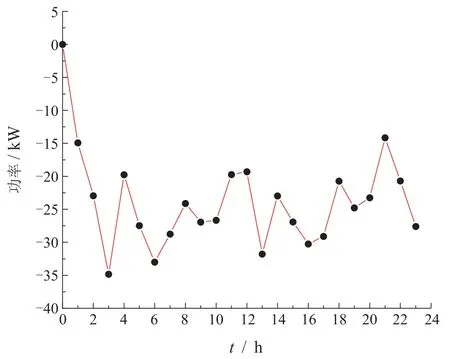
图6 主电网电力交换功率Fig.6 Exchange power between the main grid and mcirogrid

如第2.2小节所述,储能单元的荷电状态是衡量学习效果的重要指标.在各智能体行为策略执行过程中,储能单元的荷电状态,充放电状态均受智能体影响.由于智能体在学习过程中,加入了储能单元的各状态参数,因此智能体负责协作优化储能单元的荷电状态.图7-8 显示了储能单元荷电状态变化情况,训练初期各智能体无法选择有效的动作,导致储能单元荷电状态出现超出上下限的情况.由于在目标函数中加入了最优荷电状态这一优化目标,所以随着训练的进行,各智能体通过相互交互的方法,使储能单元荷电状态逐步逼近最优值.当模型训练基本完成时,单个周期内荷电状态始终在50%上下波动,符合保持在最优荷电状态这一设计要求.

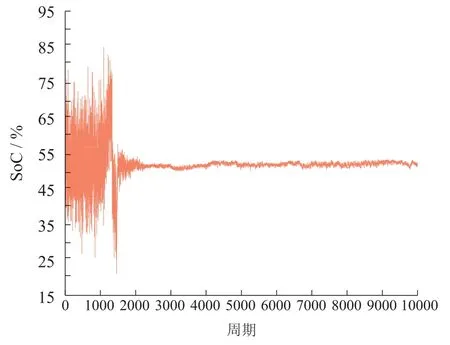
图7 10000周期SoC均值曲线Fig.7 SoC mean curve during 10000 cycles

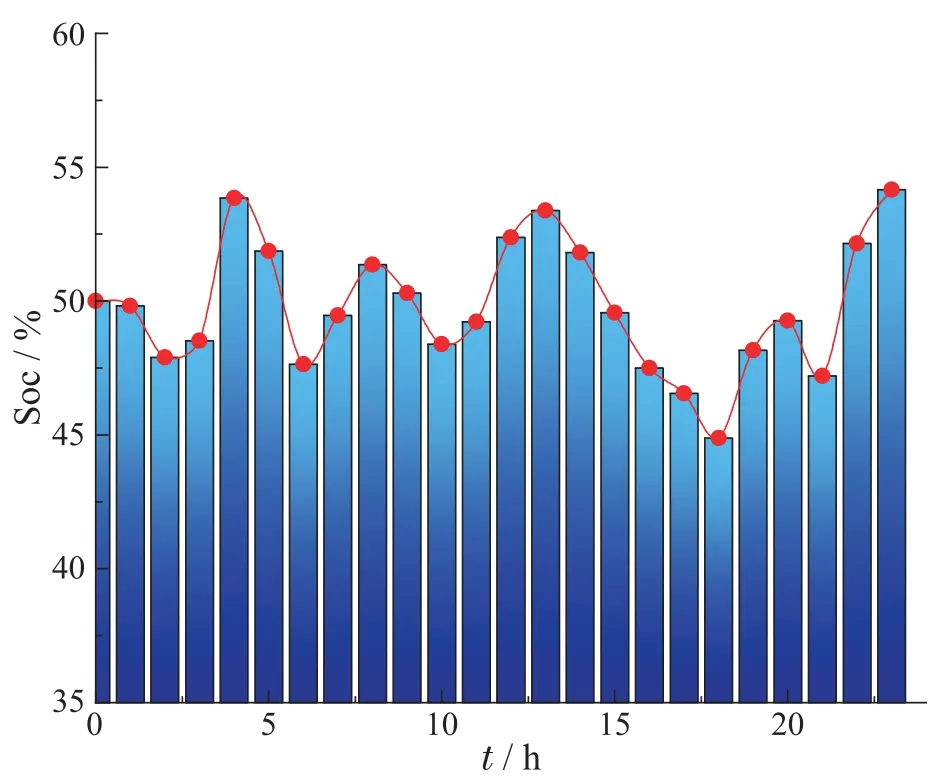
图8 储能单元SoC变化Fig.8 Variation of energy storage unit SoC

5 总结

本文针对微电网优化调度问题存在不确定性强、实时性要求高和参数空间大的问题,提出了一种基于分布式深度强化学习的实时优化调度方法,管理各发电单元、储能单元以及主电网的能源生产与调用.首先利用动作网络与本地环境进行交互,获取相应的动作策略,再根据环境参数与所选动作判断是否满足约束条件,计算奖励值;随后采用价值网络学习本地与其他智能体的神经网络参数;最后根据所学模型,对动作网络选择的动作进行反馈,使动作网络寻求更高的奖励值.本文所提出的方法在训练完成后可以快速给出优化策略,合理分配各发电单元出力,实现了微电网系统实时优化调度,有效地提高了系统响应速度,优化了系统运行成本.

在后续的研究中,将考虑结合区块链中的数据保密机制,提高分布式通信环境下数据安全性,形成更安全的优化调度方法,以期在实际的微电网系统进行应用.