基于ITD-MOMEDA联合降噪的滚动轴承故障诊断研究*

朱紫悦,张金萍

(沈阳化工大学 机械与动力工程学院,辽宁 沈阳 110142)

0 引 言

滚动轴承是机械系统中关键零部件之一,一旦出现严重故障可能会导致机器停机,造成经济损失。在实际工作过程中,轴承故障振动信号微弱,容易被强干扰信号覆盖[1]。因此,如何从振动信号中提取微弱故障特征对轴承早期故障进行精确诊断和识别,是轴承故障诊断的难题之一[2]。

在轴承故障诊断中,由于早期故障信号常被噪声所淹没,因此从信号中去噪,并增强弱故障特征至关重要[3]。而提取微弱故障特征的前提是对信号进行降噪,剔除干扰信号,增强信号的故障信息。传统的信号降噪方法有:小波变换[4](wavelet transform,WT)、经验模态分解[5](empirical mode decomposition,EMD)、局部均值分解[6](local mean decomposition,LMD)、局部特征尺度分解[7](local characteristic scale decomposition,LCD)等。

但是在信号预处理阶段,单一的方法难以有效地剔除信号的背景噪声,且信号降噪方法自身也存在模态混叠、端点效应、欠包络、计算量大等问题。

固有时间尺度分析(intrinsic time-scale decomposition,ITD)是FREI M G等人[8]在2006年提出的一种具有实时性的用于处理非平稳、非线性信号的新型时频分析方法。ITD方法克服了以上传统方法在对非线性、非平稳信号处理局限性,具有良好的时频聚集性。根据其特点,肖洁等人[9]研究了ITD降噪算法,表明ITD能够克服EMD等存在的模态混叠等问题,具有良好的自适应性;但是用单一的ITD降噪方法处理信号还是存在不少噪声。同样地,范玉刚等人[10]研究了利用ITD算法消减信号噪声干扰,但是若没有自回归模型(auto regressive,AR)的加入,难以及时捕捉早期微弱故障信号。刘丰等人[11]将ITD算法与改进的峭度解卷积(maximum correlation kurtosis deconvolution,MCKD)算法相结合,成功地去除了无关成分的干扰,并保留了敏感故障冲击成分,确保了降噪效果的准确性,表明了ITD与其他降噪方法相结合更具优越性。

最大相关峭度解卷积(MCKD)由GEOFF L M等人[12]在2012年提出。但该方法降噪效果的好坏与否受限于周期和滤波器的长度。基于此,MCDONALD G L等人[13]在2017年提出了一种新的解卷积算法,即多点最优调整的最小熵解卷积(MOMEDA)。该算法是在MCKD方法基础上发展而来,它通过简单的迭代求得最优解的滤波器,以此来增强信号的周期性冲击成分,并被成功地运用到了齿轮箱的故障诊断中。

根据以上分析,为了有效剔除微弱故障信号的背景噪声,准确清晰地提取出轴承的故障特征频率,笔者提出一种基于ITD与MOMEDA相结合的联合降噪方法,并将其应用到滚动轴承的故障诊断中。

1 基本理论

1.1 固有时间尺度分析理论

ITD法可以将非线性、非平稳信号分解为一系列的固有旋转分量(PRC)和剩余趋势分量(R)之和。

其具体的分解过程,即采样信号的一次分解过程为:

(1)

式中:Xt—采样信号;Lt—基线分量;Ht—一个PR分量;L—分段线性提取因子;P—迭代次数。

1.2 MOMEDA理论

假定原始振动信号x表达式为:

x=h*y+e

(2)

式中:y—轴承损伤点的碰撞信号;h—系统卷积函数;e—随机干扰噪声。

MOMEDA的主要目标是找到最优滤波器f,以准确地提取故障信号特征。其解卷积过程如下:

(3)

式中:L—滤波器长度。

其中:k=1,2,…,N-L。

MOMEDA引入多点D-范数,以提取故障信号的特征。多点D-范数表达如下:

(4)

(5)

式中:t—目标向量;f—滤波器向量组;y—振动信号向量。

当t与y达到一致时,其解卷积滤波效果达到最好状态,此刻fMDN(y,t)为最大值,亦fMOMEDA值最大,即MOMEDA完成了其主要目标。

由式(4)可得:

(6)

其中:f=f1,f2,…,fL;t=t1,t2,…,tN-L。

联立式(3～5)可得:

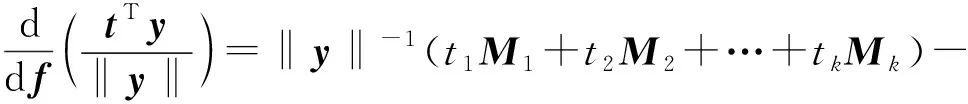
(7)

其中:X0=[M1,M2,…,Mk]。

则式(7)可以记为:

‖y‖-1X0t-‖y‖-3tTyX0y=0

(8)

经整理后可得:

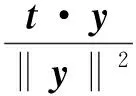
(9)

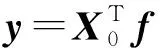
(10)

取一特解作为最优滤波器f,记为:

(11)

2 诊断流程

基于ITD-MOMEDA的滚动轴承故障诊断流程图如图1所示。

图1 基于ITD-MOMEDA的滚动轴承故障诊断流程图

具体的诊断流程如下:

(1)对轴承故障振动信号进行ITD分解,得到了多个固有旋转分量和剩余趋势分量;

(2)根据相关系数值和峭度值,对PRC分量进行了筛选;

(3)对筛选出的信号分量进行了重组;

(4)使用MOMEDA方法去除噪声,增强重构故障信息;

(5)做Hilbert包络解调分析;

(6)提取故障特征频率,完成了轴承的故障诊断。

3 仿真信号分析

3.1 基于ITD和LMD仿真信号对比

为了证明ITD方法优于传统预处理方法,笔者构造了仿真信号,通过ITD和LMD方法来对比分析说明前者方法的优越性。

信号表达式如下:

(12)

式中:x(t)—原始信号;s(t)—周期性冲击信号;n(t)—白噪声信号。

笔者提取1 000点做分析处理。

信号s(t)的时域图和频谱图如图2所示。

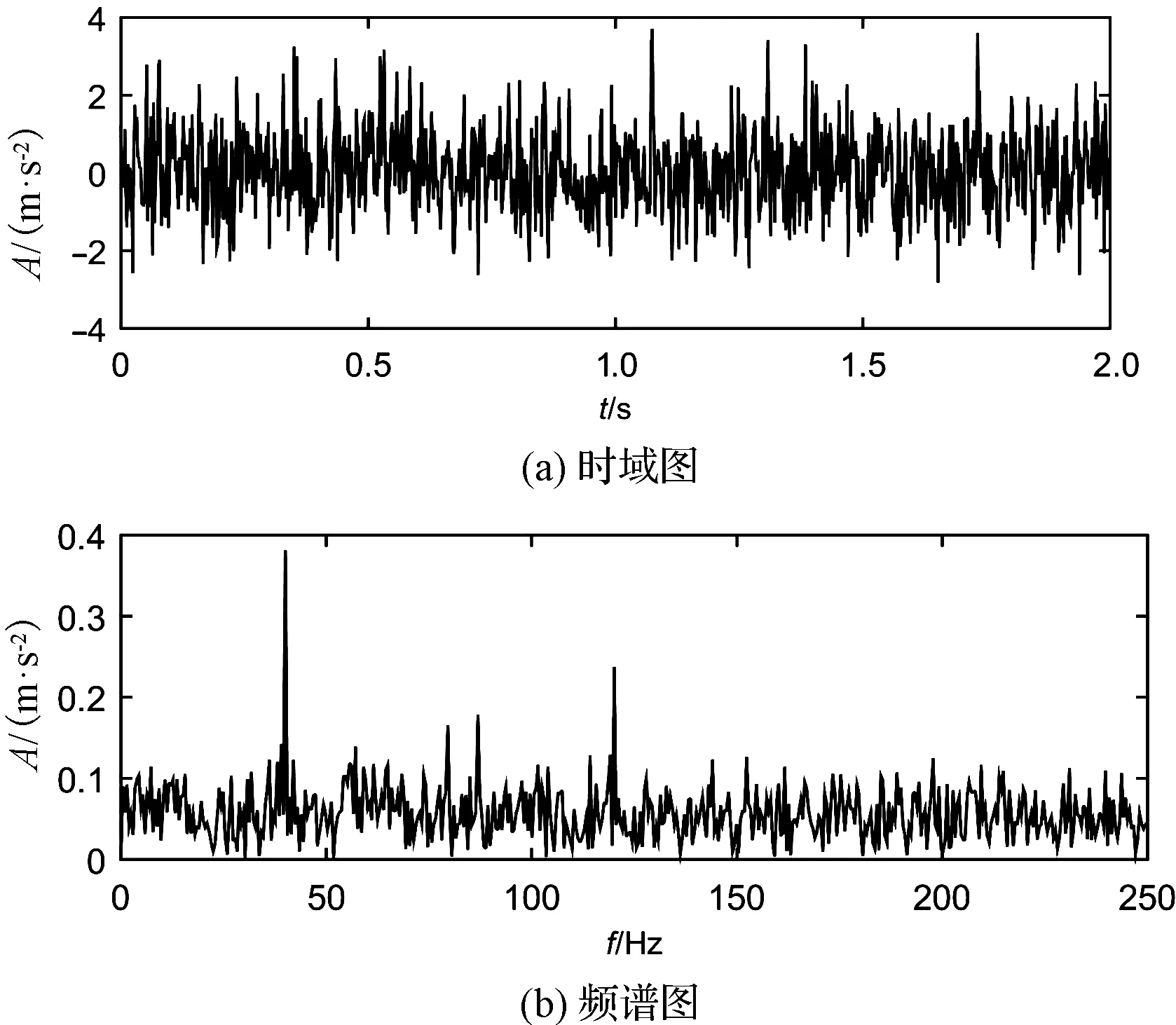
图2 信号x(t)的时域图和频谱图

由图2可知:(1)由基频为40 Hz、调频频率为15 Hz的调频调幅信号、频率为140 Hz的余弦信号构成的周期性冲击信号被白噪声完全淹没,无规律可循;(2)频谱图无明显的故障特征频率。

为了去除噪声,笔者分别引入ITD和LMD算法,进行预处理对比分析。

仿真信号经ITD和LMD分解对比图如图3所示。

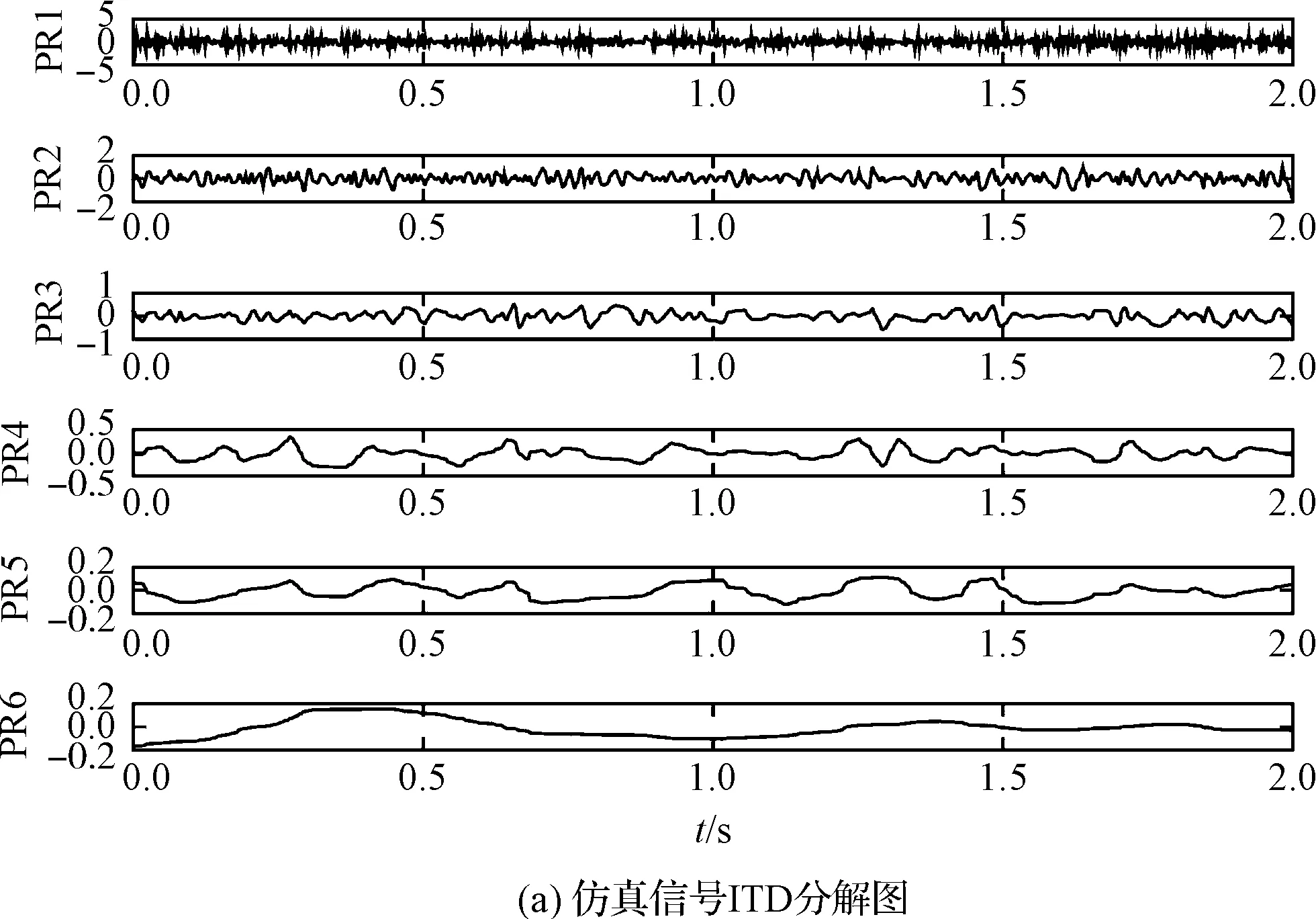
图3 仿真信号经ITD和LMD分解对比图

由图3可知:含噪信号经LMD分解后的PF2和PF3处有明显的模态混叠现象,而经ITD分解的信号则无,说明ITD比LMD方法有优势。

3.2 MOMEDA和MCKD对比分析

笔者选择由ITD分解的分量进行重构,再对重构信号分别进行MOMEDA和MCKD降噪处理。

MOMEDA和MCKD分析对比图如图4所示。

图4 MOMEDA和MCKD分析对比图

由图4可知:由于受到有限脉冲滤波器长度和背景噪声的影响,采用MCKD的降噪效果要劣于采用MOMEDA的效果。

4 实例分析

4.1 外圈故障分析

笔者选取美国辛辛那提智能维护中心的滚动轴承全寿命实验数据进行分析[14]。

该试验台由一个AC电动机(转速为2 000 r/min)、4个轴承(Rexnord ZA-2115双列轴承)、振动传感器(X轴和Y轴)组成;轴承由交流电动机通过皮带牵引,转速为2 000 r/min,同时给转轴和轴承施加约26 671 N的径向载荷,每个轴承的支座上在水平和垂直方向上安装加速度传感器,上端还装有热电偶,用来检测轴承的实时温度。

在早期的故障信号选择上,根据文献[15]的实测信号分析,笔者选用实验的第2次测试数据的5 310 min时的轴承振动数据作为实验分析对象,取10 000个数据点(此刻的转速实际为1 948 r/min);该实验结束后,外圈出现磨损,轴承1出现外圈磨损失效;根据轴承工况和结构参数计算出轴承外圈故障频率为230 Hz。

滚动轴承参数如表1所示。

表1 滚动轴承参数

笔者选取的轴承故障信号的外圈时域图和包络图如图5所示。

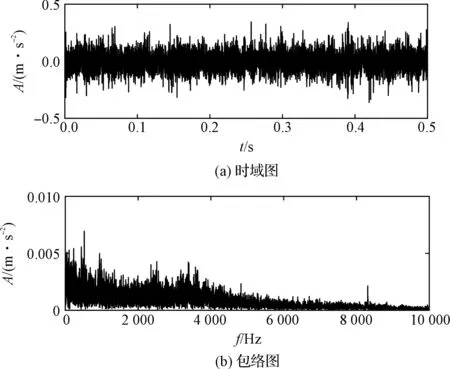
图5 外圈时域图和包络图

由图5中可知：故障特征信号被淹没在背景噪声中,无法直接进行故障判别。因此,笔者在此对外圈原始振动信号进行ITD处理。

4.2 外圈信号的ITD分解

外圈故障信号ITD分解分量如图6所示。

图6 外圈故障信号ITD分解分量图

由图6可知：各阶分量按频率高低依次排列。其与原信号的相关系数和峭度值结果,如表2所示。

表2 相关系数和峭度值

从表2中可知:PRC1至PRC3与原信号相关系数较大,分别为0.854 3、0.565 2和0.348 4;又PRC3和PRC5峭度值较大,分别为3.306 6和3.175 5均大于3,但其相关系数较小,究其原因应是噪声振动引起。又因为PRC2峭度值为2.735 7,所以笔者选择PRC1和PRC3作为重构信号的重构分量。

4.3 外圈重构信号的MOMEDA处理

笔者使用MOMEDA对重构信号进行降噪处理,周期设为86.96。

经MOMEDA降噪后的时域图和包络图如图7所示。

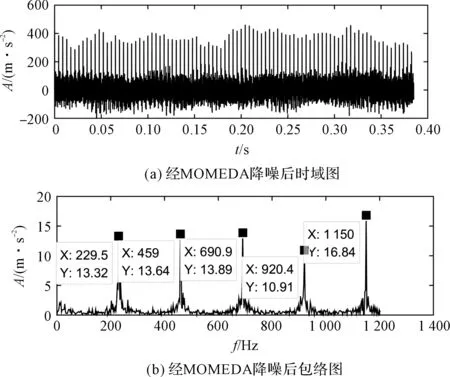
图7 重构信号MOMEDA降噪后时域和包络图

由图7可知:时域图特征频率峰值突出,噪音明显减少;在包络图中可以清晰地看出与外圈故障特征频率230 Hz较接近的229.5 Hz,和其2倍频459 Hz,直到5倍频1 150 Hz等。

该结果证明,采用此法能够提取被噪声淹没的轴承故障特征。

4.4 外圈重构信号的MCKD处理

为与MOMEDA方法进行比较,笔者用MCKD方法对重构信号进行降噪处理。

经MCKD降噪后的时域和包络图如图8所示。

图8 经MCKD降噪后时域和包络图

由图8可知:在包络图中,外圈故障特征冲击频率不能被精确地提取,准确率较笔者提出的方法低4.3%;且其周期性较弱,干扰频率毛刺较多。

5 泛化研究

5.1 内圈故障分析

笔者以美国西储大学滚动轴承数据中心的实验数据[16]为例来分析轴承振动信号,即取在12 000 Hz采样频率下采集的驱动端SKF6205轴承内圈含有的故障信号数据进行分析。

其中,实验时轴承的转速是1 750 r/min。实验滚动轴承节径是39.04 mm,滚动体个数是9个,滚动体直径是7.94 mm,内圈直径25 mm,外圈直径52 mm,接触角是0°。通过参数计算可得,该轴承内圈故障频率为158 Hz。

内圈故障信号的时域图及包络图如图9所示。

图9 内圈故障信号时域图及包络图

由图9可知:故障特征信号被淹没在背景噪声中,无法直接进行故障判别,需进行降噪处理。

5.2 内圈信号的ITD分解

接下来,笔者对轴承内圈的原始振动信号进行ITD处理。

内圈故障信号ITD分解分量如图10所示。

图10 内圈故障信号ITD分解分量

由图10可知：各阶分量按频率高低依次排列。其与原信号的相关系数和峭度值结果如表3所示。

表3 相关系数和峭度值

从表3中可以看出:PRC1和PRC2的相关系数较大分别为0.955 9、0.482 3;又PRC1至PRC5峭度值均大于3,但PRC3和PRC4相关系数较小,应是噪声振动所引起的。

根据以上结果,所以笔者选择PRC1和PRC2作为重构信号的重构分量。

5.3 内圈重构信号的MOMEDA处理

笔者使用MOMEDA对重构信号进行降噪处理,周期设为76。

经MOMEDA降噪后,重构信号的时域图和包络图如图11所示。

图11 重构信号经MOMEDA降噪后时域图和包络图

由图11可知:时域图特征频率峰值突出,故障信息丰富,且有规律可循;在显示的包络图中,可以清晰地提取到内圈故障特征频率的倍频,成功诊断出轴承故障位置发生在内圈。

5.4 内圈重构信号的MCKD处理

为与MOMEDA方法进行比较,笔者用MCKD方法对重构信号进行降噪处理。

经MCKD降噪后,重构信号的时域和包络图如图12所示。

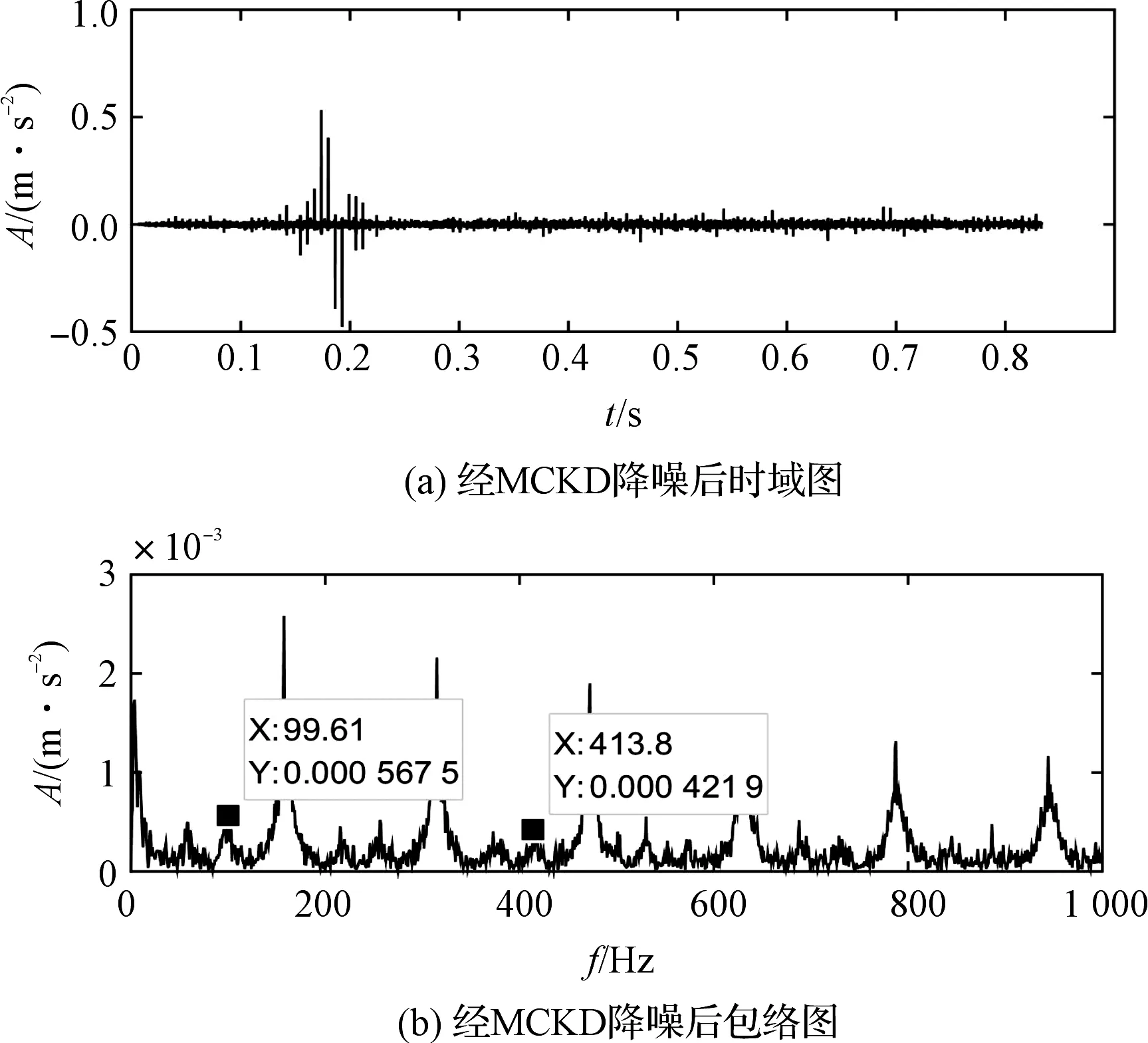
图12 重构信号经MCKD降噪后时域和包络图

由图12可知:在包络图中,内圈故障特征冲击频率不能被精确地提取;虽有冲击特征,但频率幅值低,且干扰频率较多,不能进行故障特征频率的有效提取。

6 结束语

为了更好地提取和识别出轴承的故障信号,笔者提出了一种基于固有时间尺度分析(ITD)和多点最优调整的最小熵解卷积(MOMEDA)相结合的联合降噪方法,并将其应用于滚动轴承的故障诊断中;首先，将ITD算法作为MOMEDA前置滤波降噪技术手段,对滚动轴承故障信号进行了分解,挑选出故障特征丰富的有用信号分量,并对其进行了重构;然后，用MOMEDA方法对重构信号进行了再次降噪,用包络解调技术解调出了故障特征频率。

研究结果表明:

(1)通过ITD和LMD对仿真信号分析,前者在分解结果上能避免模态混叠等问题,准确分解出原始信号故障信息;

(2)经对轴承外圈故障实例的分析可知,在降噪滤波方面,由于受滤波器长度和周期的影响,与MOMEDA相比,MCKD的降噪效果要明显劣于MOMEDA;与ITD-MCKD法相比,ITD-MOMEDA法的准确率提高了4.3%,且得出的时域图和包络图规律明显,峰值突出,能有效地增强信号的冲击特征,准确识别故障特征。

由于此处的实例均为单点故障,MOMEDA算法对其有良好的自适应性。若将其用于诊断复合故障,由于MOMEDA在滤波时,信号长度(与原始信号相比)缩短了;同时,该方法无法自动识别故障的脉冲周期。因此,在进行故障诊断时,需每次分别设置故障周期,致使分析的效率低下,且计算量大。

因此,在后续的研究中,笔者将对此进行深入研究,并提出相应的改进方法,以更好地适应复合故障的诊断。