BEAVRS堆芯k eff的敏感性与不确定性分析

秦凯文 杨 波,2 刘义保,2 张洁茹 郝鹏飞 刘豪杰

1（东华理工大学核科学与工程学院 南昌 330013）

2（东华理工大学核资源与环境国家重点实验室 南昌 330013）

核数据作为反应堆堆芯物理计算的重要输入参数，其不确定性会进行传递，影响堆芯物理计算结果（如有效增殖系数keff）的精度，堆芯物理计算结果的偏差会影响反应堆安全性。近年来，国内外对核数据敏感性与不确定性开展了大量的研究工作，杨群等［1］基于熔盐冷却球床堆计算出k∞不确定性主要来源于7Li（n，γ）反应截面。Ziani等［2］为了评价核数据对反应堆安全的影响，计算出摩洛哥TRIGA Mark II研究堆keff的不确定性主要来源于235U的平均裂变中子数。郝琛等［3−4］研究了不同堆芯中235U、238U和239Pu物质含量不同导致不同核素反应的不确定性差别很大。万承辉等［5］基于抽样理论研究了用于反应堆物理计算的不确定度分析方法，开发了反应堆物理计算不确定度分析程序UNICORN。丘意书等［6］基于反复裂变几率法，在连续能量蒙特卡罗程序RMC基础上开发了敏感性分析功能，计算结果与SCALE6.1［7］中TSUNAMI-3D［8］的 计 算 结 果 相 符。现阶段主要研究工作集中于计算软件的研发、计算方法的改进，较少考虑反应堆运行时燃料富集度变化、堆芯温度变化情况下核数据对keff的敏感性与不确定性的影响。本文基于美国橡树岭国家实验室开发的SCALE6.1程序［7］中KENO［7］、TSUNAMI-3D模块［8］，以麻省理工学院发布的反应堆模拟评估和验证 基 准BEAVRS［9］（Benchmark for Evaluation and Validation of Reactor Simulations）第一循环热态零功率为物理模型，开展了keff的敏感性与不确定性计算，分析了反应堆燃料富集度下降、堆芯温度上升情况下keff敏感性与不确定性，并明确了对堆芯keff敏感性与不确定性影响最大的核反应截面。

1 敏感性与不确定性理论方法

敏感性和不确定性分析的方法通常可分为随机抽样法与确定论法。随机抽样法是根据方差及协方差的大小采用蒙特卡罗方法对输入参数进行抽样，产生巨量输入参数进行输运计算，可得keff的不确定性，再计算敏感性系数［5］。该方法原理简单，但计算量大、计算时间长。确定论法首先分析出keff对核数据敏感性系数，然后根据核数据的协方差矩阵计算出keff的不确定性［10］。这类方法计算效率高，是目前核数据对keff敏感性与不确定性分析的主流方法。

设反应堆物理计算特征响应参数R为核数据的函数，根据一阶不确定性传递关系，确定论方法中不确定性的理论计算公式——Sandwich Rule［11］如下：

式中：COV(R)为特性响应参数R的相对方差；S为相对敏感性系数矩阵；ST为S向量的转置；C为核数据相对协方差矩阵。

C一般可以从评价核数据库中得到，因此不确定性计算的关键是求出敏感性系数。在反应堆物理计算过程中，特征响应参数R对输入参数α的相对敏感性定义为：特征响应参数R(α)的变化量与导致其变化的输入参数α(ξ)的相对变化量之比，即：

式中：α(ξ)为核数据（核反应截面、中子通量密度、原子核密度、能量角分布等）；ξ为相空间变量(r，Ω，E)。

核数据对中子注量率、功率分布、keff、反应性系数等物理量均会产生不确定性，本文以keff为研究对象，根据一阶微扰理论，keff对核数据的相对敏感性Skeff，α为：

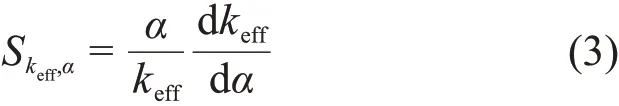
反应堆物理计算主要包括共振计算和输运计算。如果只考虑参数扰动在输运方程中的作用，这种直接影响称为显式敏感性；如果考虑参数在共振计算过程中对共振截面的作用，继而间接影响到输运方程的求解结果，则称为隐式敏感性［12］。总的敏感性系数为显式敏感性系数和隐式敏感性系数之和［13］：

2 BEAVRS简介及建模

BEAVRS压水堆模型的几何结构径向包括堆芯网络组件、堆芯围板、堆芯桶状隔板、中子屏蔽板和反应堆压力容器，轴向包括支撑板、插孔板、铬镍合金隔板和锆合金隔板等［14］。堆芯含有193个燃料组件，组件按17×17方形排布，含有264根燃料棒、24根导向管和1根中子测量管。其中燃料棒按照富集度不同，可划分为1.6%、2.4%和3.1%，高富集度燃料分布在堆芯外侧，中低富集度燃料交叉分布在堆芯内侧。导向管中可插入可燃毒物棒以及控制棒。

基 于SCALE6.1程 序 包 中KENO模 块［7］对BEAVRS进行堆芯物理建模（图1），以第一循环热态零功率为研究对象，计算了5种典型硼浓度下的keff。SCALE6.1反应截面库采用ENDF/B-VII.0库［15］，每代投入100 000个粒子，共计算了500代，舍弃前250代以减小误差。keff计算结果如表1所示，计算结果与模型基准值（keff=1.0）最大偏差不超过90×10−5（相对误差为95%置信区间）。

图1 SCALE6.1输出BEAVRS堆芯几何图 (a)径向剖面图，(b)轴向剖面图Fig.1 Geometriesof BEAVRScoreby SCALE6.1 (a)Radial geometry,(b)Axial geometry

表1 有效增值系数k eff计算结果Table 1 The calculation results of effective increment coefficient k eff

3 敏感性与不确定性分析

3.1 不同核数据敏感性系数

TSUNAMI-3D模块专门用于敏感性与不确定性分析，利用SCALE6.1程序自带的ENDF/B-VII.0多群截面数据库，执行并群和共振自屏计算，可计算隐式敏感性系数，以分析共振自屏对反应截面的影响。其通过分别执行一次前向输运计算和伴随输运计算来获得通量和伴随通量的信息［16］。选取BEAVRS热态（565 K）零功率工况，分别计算了反应堆堆芯各核素、各反应截面导致keff的敏感性与不确定性。表2给出了对keff不确定性影响最大的几种反应截面的敏感性系数。

从表2可知，235U、238U、10B、1H是keff敏感性的主要来源，235U和1H的总截面敏感性系数为正值，238U和10B的总截面敏感性系数为负值。原因在于235U作为反应堆主要裂变核素，可产生中子，1H作为轻元素，有着最大的平均对数能降，均与keff为正相关。238U与10B的吸收截面对keff影响最大，均与keff为负相关，其中238U对中子的吸收以（n，γ）反应为主，10B对中子的吸收主要以（n，α）反应形式存在。

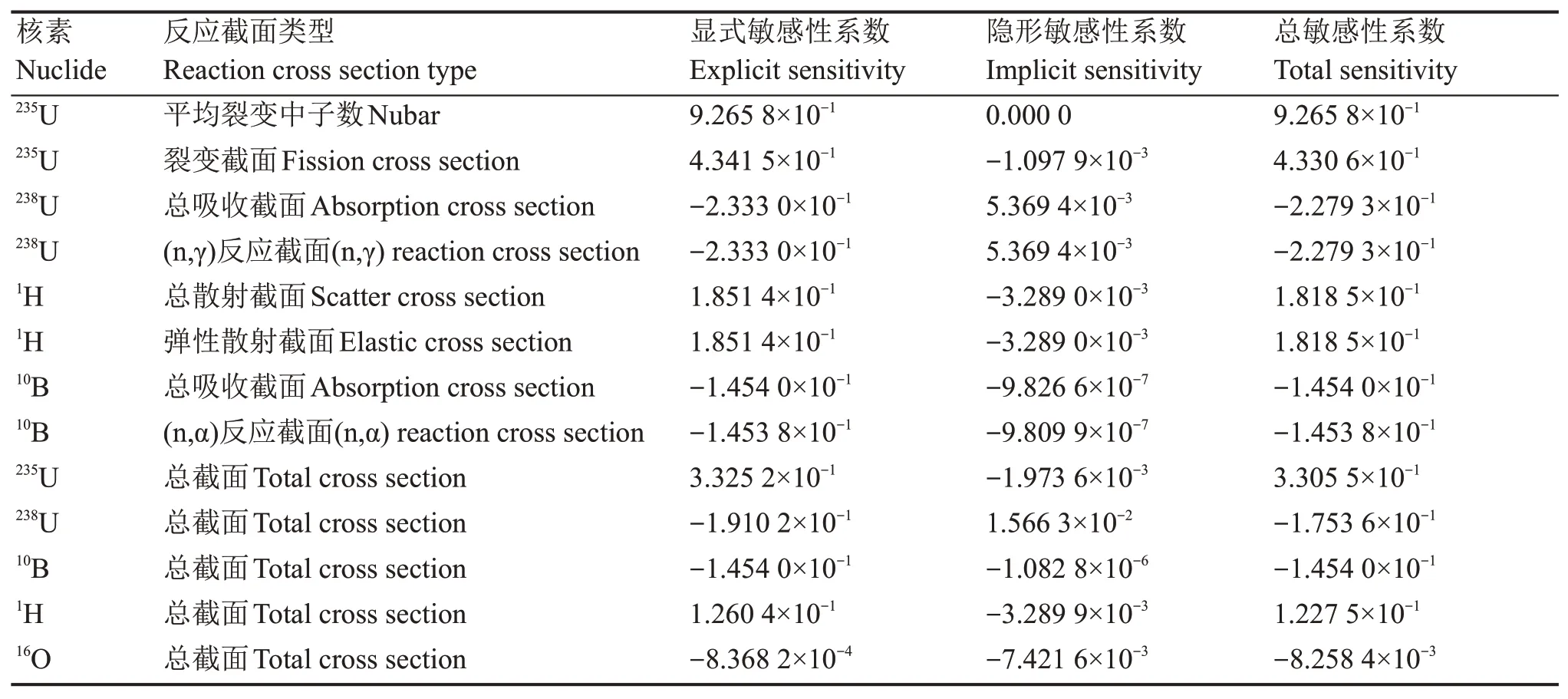
表2 不同核数据敏感性系数Table 2 Sensitivity coefficients of different nuclear data

通过敏感性计算，得出了235U、238U的总截面、平均裂变中子数、裂变截面和（n，γ）反应截面的敏感性系数随能量变化的趋势（图2、图3）。从图2可知，keff对235U平均裂变中子数和裂变截面的敏感性系数在低能区出现了峰值，是因为在该能量区间内235U容易发生裂变导致的，而（n，γ）反应截面在该区域出现了谷值，表明在热能区235U有着较大的吸收截面。从图3可知，keff对238U的裂变截面敏感性系数在高能区出现了峰值，这是由于快中子可引发238U裂变，而（n，γ）反应截面在低能区出现谷值，并且在中能区出现了强烈的波动，表明了共振吸收对keff的影响。

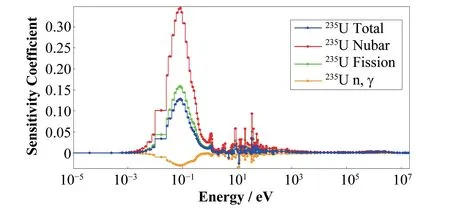
图2 235U不同核反应截面敏感性系数曲线Fig.2 Sensitivity coefficient curves of 235U at different nuclear reaction cross sections

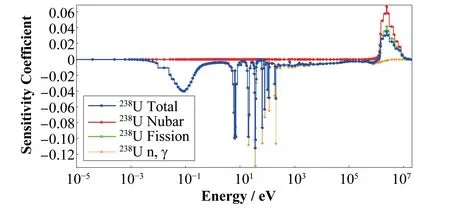
图3 238U不同核反应截面敏感性系数曲线Fig.3 Sensitivity coefficient curves of 238U at different nuclear reaction cross sections

3.2 不确定性计算

为保证与敏感性计算时使用的多群截面核数据库一致，本文选取ENDF/B-VII.0评价核数据库制作了多群协方差数据，代入式（1）即可计算出keff的不确定性。表3给出了对keff不确定性影响最大的几种核素截面。

表3 不同核数据对k eff的不确定性Table 3 Uncertainty of k eff from different nuclear data

核数据对BEAVRS模型keff总的不确定性为0.501 6%，其中238U（n，γ）反应截面导致的不确定性最大，为0.298 14%，其会导致堆芯物理计算结果keff出现较大误差，从而影响反应堆的运行安全，在实际应用中需重点关注。238U（n，γ）反应截面的敏感性系数小于235U平均裂变中子数的敏感性系数，但是238U（n，γ）反应截面对keff的不确定性却是大于235U平均裂变中子数的，所以下文对235U平均裂变中子数和238U（n，γ）反应截面对keff的不确定性影响展开进一步分析。

4 不确定性影响因素

4.1 燃料富集度的影响

随着反应堆运行时间的增加，堆内裂变材料的消耗，燃料富集度将逐渐减小。为了研究燃料富集度对keff敏感性与不确定性的影响，计算了不同富集度下燃料组件中235U平均裂变中子数和238U（n，γ）反应截面对keff的敏感性系数和不确定性，结果如表4所示。

表4 不同富集度对k eff的敏感性与不确定性Table 4 Sensitivity and uncertainty of different enrichment degrees to k eff

随着燃料富集度的降低，235U平均裂变中子数的敏感性系数减小，238U（n，γ）反应截面的敏感性系数增大。其原因为当燃料富集度下降时，235U相对含量降低，238U相对含量增加，导致中子能谱硬化。238U（n，γ）反应截面由于能谱变硬而增强，从而对keff不确定性超过235U平均裂变中子数。

4.2 温度变化的影响

堆芯由冷态到热态，温度变化200~300 K，从而引起238U的共振吸收峰多普勒展宽，吸收中子能力增强。为研究堆芯温度变化对keff敏感性与不确定性的影响，计算了不同温度下235U平均裂变中子数和238U（n，γ）反应截面对keff的敏感性系数和不确定性，结果如表5所示。

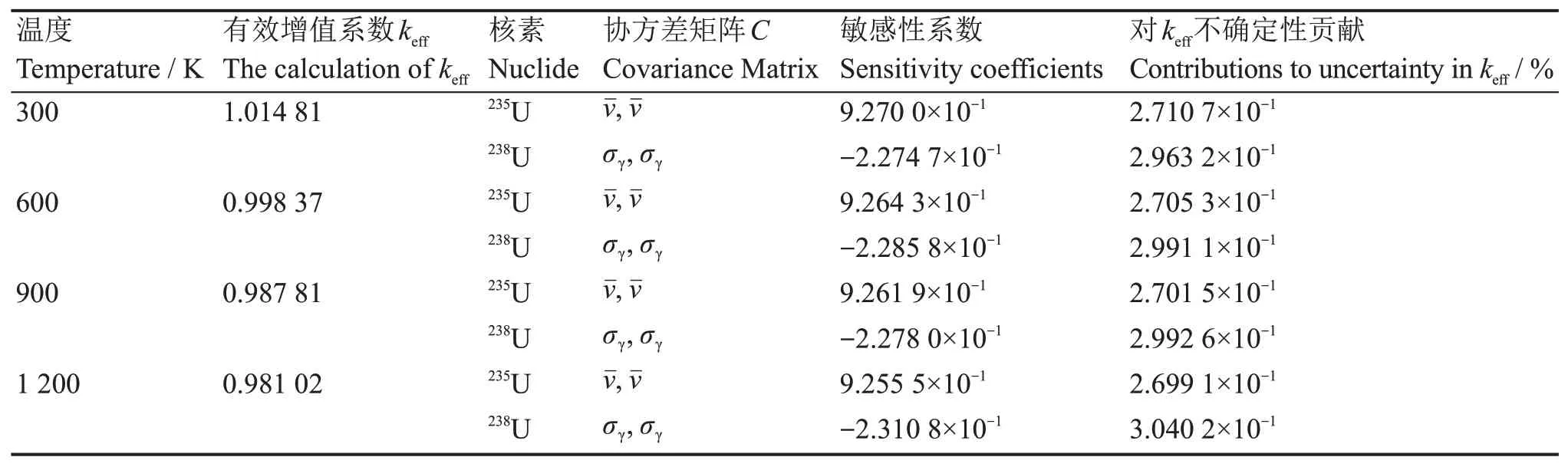
表5 不同温度对k eff的敏感性与不确定性Table5 Sensitivity and uncertainty of different temperatureto k eff

由表5可知，随着反应堆温度上升，235U平均裂变中子数对keff的不确定性减小，238U（n，γ）反应截面对keff不确定性增大。其原因为当堆芯温度上升时，多普勒效应［17］展宽了238U共振吸收峰，引起了238U低能部分（n，γ）反应截面增加；同时慢化剂密度减小，中子慢化能力下降，中子能谱变硬，导致keff减小，使得238U（n，γ）反应截面对keff不确定性不断增大，从而超过235U平均裂变中子数。

5 结语

本文以压水堆BEAVRS堆芯热态零功率为研究对象，利用SCALE6.1程序包中KENO模块建立堆芯物理模型，采用TSUNAMI-3D模块对反应堆堆芯燃料材料、结构材料及冷却剂材料等70多种核素的反应截面开展keff的敏感性与不确定性分析，分析了不同燃料富集度、不同温度对keff敏感性与不确定性的影响。计算结果表明：核数据不确定性导致BEAVRS模型keff总的不确定性为0.501 6%，235U平均裂变中子数的敏感性导致keff的敏感性系数最大（0.926 58），238U（n，γ）反应截面对keff不确定性贡献最大（0.298 14%）。反应堆燃料富集度下降、堆芯温度上升时，虽然235U平均裂变中子数不确定性导致keff不确定性减小，但是238U（n，γ）反应截面不确定性导致keff不确定性增大。因此在开展反应堆堆芯物理计算时，应重点关注238U（n，γ）反应截面的数据信息，同时核反应截面的敏感性和不确定性分析结果也为核数据库完善提供参考。

作者贡献声明秦凯文负责建立模型、实施研究、分析数据并起草文章初稿；杨波负责提供理论支撑，文章修改；刘义保主负责设计具体研究内容和方向，提出合理化研究方案；张洁茹负责收集文献资料；郝鹏飞负责数据处理，提供技术支持；刘豪杰负责文章校对，分析总结。