基于有效驱替通量的油藏物性综合时变数值模拟技术及应用

赵平起, 沈泽阳, 蔡明俊, 张家良, 姜瑞忠,赵 明, 芦风明, 李晓良, 何书梅, 李佩敬

(1.中国石油大港油田公司,天津 300280; 2.中海石油(中国)有限公司天津分公司,天津 300451;3.中国石油大学(华东)石油工程学院,山东青岛 266580)

国内油田大多进行注水开发,常年水驱造成储层物性不断变化[1]。尤其油田进入高含水、高采出程度时期后,其储层物性特征相对于原始状态已发生明显改变。储层物性改变必然会造成驱替特征的改变,进而影响剩余油分布规律和油田整体开发效果[2]。为精确模拟剩余油分布,有必要明确储层空间和流体的时变规律,完善储层时变数值模拟技术,国内外不少学者对此进行了研究。盖英杰等[3-5]建立多个阶段的动态模型,利用重启动的方法实现了时变数值模拟,但模拟是间断的、不连续的,存在一定局限性[6];姜瑞忠等[7]利用含水饱和度定量表征储层物性变化,并实现连续时变数值模拟,但其受开发制度的影响会产生跳跃现象;鞠斌山等[8-10]实现了基于含水率的时变数值模拟技术,但初始条件存在可动水时会干扰时变计算;李晓燕等[11-13]利用冲刷倍数表征物性时变,但模拟结果易受网格划分的影响;姜瑞忠等[14-15]、Sun等[16]利用面通量表征水驱强度,解决了其他参数表征存在的问题,但对于相同尺寸不同孔隙度的岩心无法区分水驱强度的差异,有待进一步完善。笔者在前人研究基础上,提出有效驱替通量这一指标用以表征水驱强度,并利用其实现储层空间和流体时变规律的表征,实现基于驱替通量的综合时变数值模拟技术,为高含水期剩余油精确预测奠定基础。

1 综合时变表征

时变规律的表征方法有很多,可划分为定量表征法、多因素法、单因素法3类。考虑到定量表征法更为客观,且表征连续,易与数值模拟有效结合,故选用定量表征法描述储层物性的时变规律,并将表征结果运用于油藏数值模拟。

1.1 时变表征参数选取

综合考虑各种参数的优缺点,创新提出有效驱替通量的概念,用以表征水驱强度。有效驱替通量是指单位孔隙截面积下累积流过水的体积,其表达式为

F=Qw/(Aφ).

(1)

式中,F为有效驱替通量,简称驱替通量,m3/m2;Qw为岩心截面累积流过的水量,m3;A为岩心横截面积,m2;φ为岩心的孔隙度。

将驱替通量和面通量进行对比。相同注入量Q,对于相同尺寸孔隙度分别为φ1和φ2的两块岩心,面通量均为Q/A,即水驱强度相同,与事实不符。孔隙度较小的岩心,其孔道相对较小,相同水量下孔道受到水的冲刷程度更高,但面通量无法有效反映。驱替通量则考虑了孔隙度的影响,解决了面通量的缺陷,可准确反映二者水驱强度差异,其值分别为Q/(Aφ1)和Q/(Aφ2),与事实吻合,可见采用驱替通量表征水驱强度更为准确。

在数值模拟任意三维网格内,水会沿着x、y、z方向流动,每个截面均会有水流入或流出。因此每个网格的总驱替通量就是各个方向上的驱替通量之和。

总驱替通量定义为

Ft=∑Fd=Fx+Fy+Fz.

(2)

x、y、z各个方向的驱替通量的定义为

(3)

式中,Ft为总驱替通量,m;Fd为x、y、z方向的驱替通量,m;Qxw、Qyw和Qzw分别为网格x、y、z方向上水流入或流出的累积体积,m3;Ax、Ay和Az分别为网格x、y、z方向的横截面积,m2。

1.2 渗透率时变规律表征

利用B油田11口井的试井资料解释出各井区在不同时间点的渗透率,再结合数值模拟软件计算出对应时间点下各井区的平均驱替通量,并对二者进行拟合,结果如图1所示。随着驱替通量增加,储层渗透率变大,整体呈指数关系。

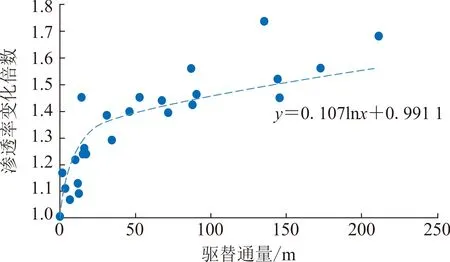
图1 B油田渗透率与驱替通量的关系Fig.1 Relationship between permeability and displacement flux in B Oilfield

1.3 原油黏度时变规律表征

将不同时间点测得的油藏温度下地面脱气原油黏度与模拟计算出的各井区的平均驱替通量进行对比分析(图2)。由图2可以看出,随驱替通量增加,原油黏度增大,二者同样呈指数关系。这是因为油中的轻质组分更易被水冲刷带出,储层原油中重质组分占比增加,黏度增大[17]。

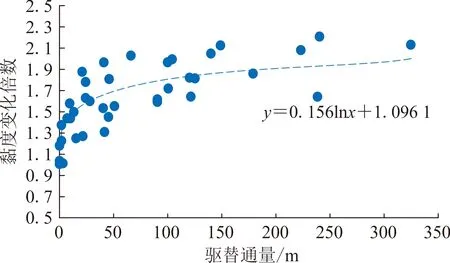
图2 原油黏度和驱替通量的关系Fig.2 Relationship between viscosity of crude oil and displacement flux

1.4 相渗曲线时变规律表征

相渗曲线可采用幂函数经验公式定量计算,即

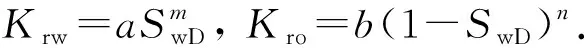
(4)

其中

式中,Kro和Krw分别为油相和水相相对渗透率;Swc为束缚水饱和度;Sor为残余油饱和度;Sw为含水饱和度;m和n为受岩石孔隙结构影响的指数。

相对渗透率曲线形态可由Swc、Sor、Krw(Sor)、拟合指数m和n表征。根据相似油田某试验不同驱替通量下得出的相渗曲线,将相渗时变规律细化为这5个参数随驱替通量的变化(图3)。

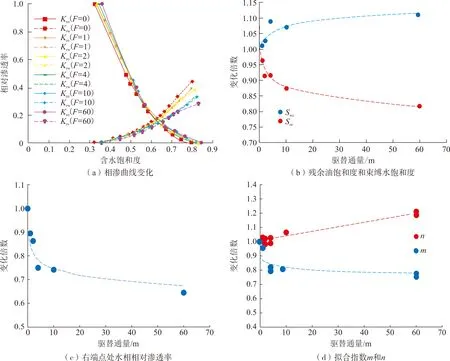
图3 相渗曲线和特征参数与驱替通量的关系Fig.3 Relationship between relative permeability and displacement flux

根据图3,随着驱替通量增加,束缚水饱和度变大,残余油饱和度变小,油相相对渗透率曲线整体有所抬升但趋于下凹,水相相对渗透率整体会逐渐下移但趋于上凸。拟合得出的相渗曲线5个特征参数与驱替通量的函数关系为

Swcc=0.023lnF+1.021 1,

(5)

Sorc=-0.034lnF+0.954 3,

(6)

Krwc=-0.041lnF+0.842 2,

(7)

mc=-0.022lnF+0.864 8,

(8)

nc=0.003 3F+1.005 9.

(9)

式中,Swcc为束缚水饱和度变化倍数;Sorc为残余油饱和度变化倍数;Krwc为残余油饱和度下水相相对渗透率变化倍数;mc为水相相对渗透率曲线拟合参数m的变化倍数;nc为油相相对渗透率曲线拟合参数n的变化倍数。

利用式(5)～(9)可以根据实际驱替通量修正不同时刻下的相渗曲线,实现相渗曲线的时变表征。

2 综合时变数值模拟

2.1 数学模型

考虑原油黏度、储层渗透率和相对渗透率曲线的时变规律,建立基于驱替通量表征的油藏时变模型。

油相:

(10)

水相:

(11)

气相:

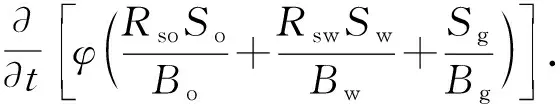
(12)

式中,qvo、qvg和qvw分别为在单位体积和时间条件下流入或流出的油、气、水各相流体的体积,m3/s;po、pg和pw分别为油、气、水三相的压力,Pa;Rsw为溶解气水比;Rso为溶解气油比。

其他辅助方程、初始条件和边界条件与常规黑油模型一致,微分方程中的原油黏度、渗透率和相对渗透率不再是常数,变成与驱替通量相关的函数。

2.2 模型求解

根据上述时变数学模型,开发时变数值模拟软件。该软件模型的求解与黑油模型的求解相似。首先,利用有限差分方法对微分方程进行离散,采用全隐式算法求解压力和饱和度。

油相微分方程为

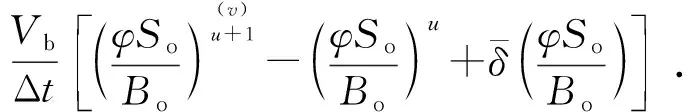
(13)

水相微分方程为

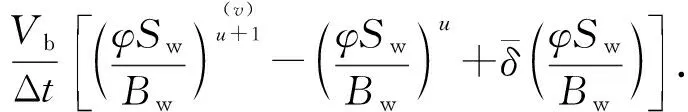
(14)

气相微分方程为

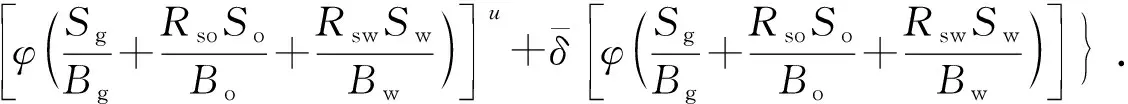
(15)

其中

Qvo=Vbqvo,Qvw=Vbqvw,Qvg=Vbqvg,

式中,u为时间步;v为迭代步;l为流体类型,油相为o、气相为g、水相为w;Tl为l相流体的流动系数;Φl为l相流体的势;A为网格截面积,m3;Bl为l相流体的体积系数;μl为l相流体的黏度,mPa·s;L为网格长度,m;D为深度,m。

在每个时间步结束时,将计算每个网格的方向驱替通量和总驱替通量。然后,根据试验或矿产资料分析获得的物性时变规律,重新计算每个网格驱替后的原油黏度、渗透率和相渗曲线,进而修正各网格的传导率。

3 不同时变参数对开发效果的影响

为进一步分析各时变参数对开发效果的影响,建立五点井网概念模型进行数值模拟,网格划分为55×55×15,平面步长10 m,纵向步长1 m。油藏顶部深度为1 200 m,有效厚度为12 m,孔隙度为30%,x、y、z方向渗透率分别为1 240×10-3、1 240×10-3、124×10-3μm2。初始含油饱和度为0.685,水的密度为1 g/cm3,油的密度为0.906 g/cm3,水的压缩系数为4.67×10-4MPa-1,水的体积系数为1.013。设计不考虑时变、相渗时变、黏度时变、渗透率时变、综合时变5种模拟方案。

通过时变软件模拟得到各方案的累积产油曲线和含水率曲线(图4)。同时,进一步对各模型的驱替特征、平面与纵向剩余油分布进行分析。由于束缚水饱和度的变化,相渗时变和综合时变的见水时间会明显后移,无水采油期增长。各类时变模型含水率由高到底依次为黏度时变、渗透率时变、不时变、综合时变和相渗时变,采出程度则正好与之相反。

图4 不同时变参数开发曲线比较Fig.4 Comparison of development with different time-varying parameters

3.1 黏度时变下剩余油分布特征

图5为黏度时变与不时变的剩余油分布对比。从整体剩余油饱和度分布角度来看,各典型井网下考虑黏度时变的模型剩余油都高于不考虑时变的模型。黏度时变会造成优势通道黏性指进现象的加剧,使注入水迅速向生产井窜进,可能提高波及速度和范围,但易造成驱替前缘不均匀,降低洗油效率,从而导致开发效果变差,近井附近和储层底部剩余油相对较高。

图5 黏度时变与不时变剩余油分布Fig.5 Residual oil distribution of time-varying viscosity and not considering time-varying

3.2 渗透率时变下剩余油分布特征

图6为渗透率时变条件下五点井网的含油饱和度场。从图6中可以发现,对于底部强水淹的优势通道,注入水冲刷强度大,驱替通量快速增加,渗透率变大,加剧了储层非均质性,进而造成底部强冲刷区域渗流优势逐渐增强,使注入水优先沿着底部优势通道向生产井窜进,含水率迅速提高,造成注入水无效循环,波及和洗油能力相对变差,剩余油饱和度略高。

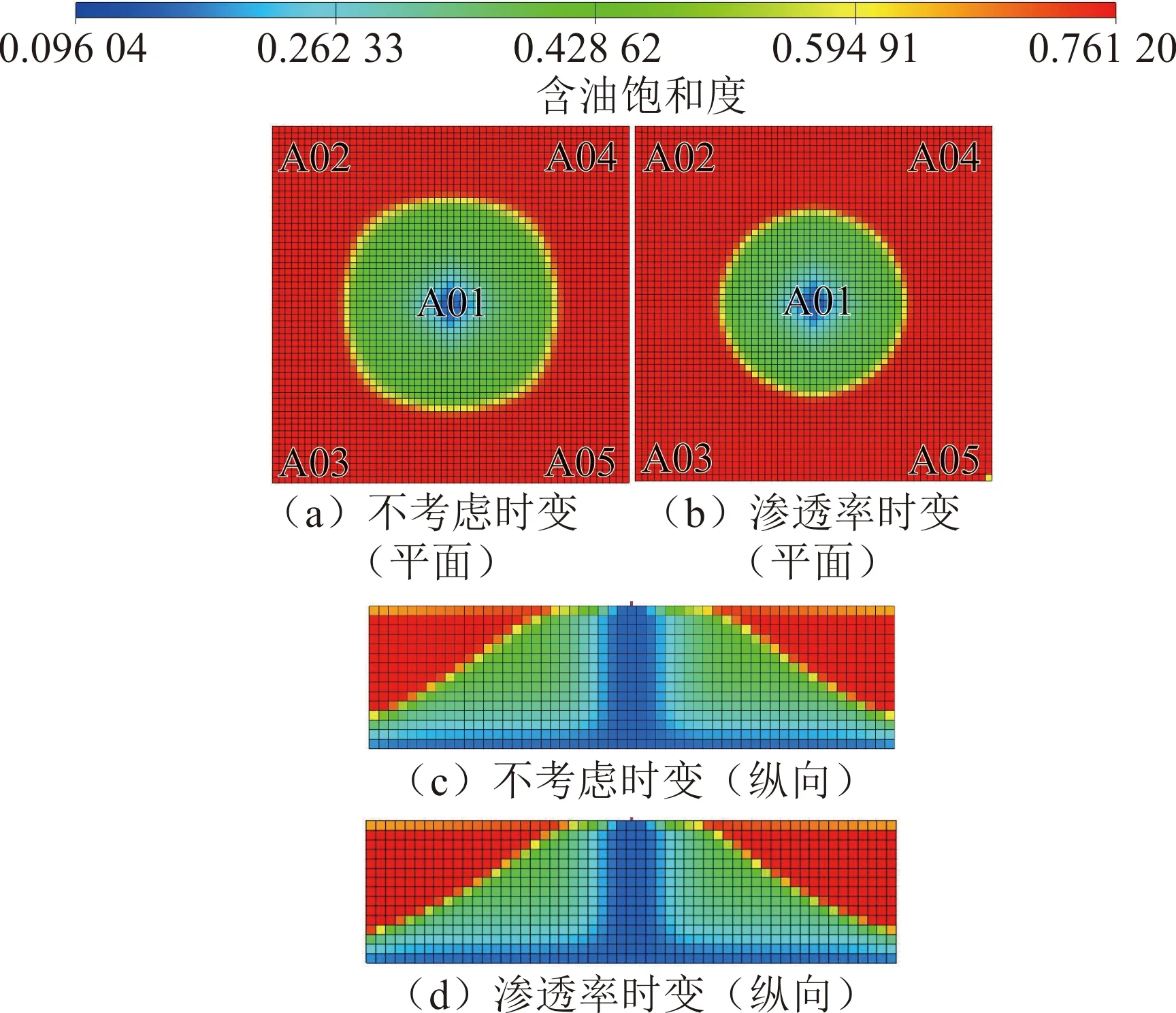
图6 渗透率时变与不时变剩余油分布Fig.6 Residual oil distribution of time-varying permeability and not considering time-varying

3.3 相渗曲线时变下剩余油分布特征

图7为相渗时变与不时变的剩余油对比。随着注水的不断冲刷,相渗曲线整体向右偏移,油相和水相相对渗透率曲线分别抬高和降低,水油流度比降低,油更容易被驱出。由于近井地带和底部优势水淹层受注水冲刷强度较大,剩余油相应较少。同时,残余油饱和度降低表明洗油效率增强,采出程度相应提高。总的来说,考虑相渗曲线时变更有利于驱油,开发效果会得到明显改善。

图8为综合时变与不时变的剩余油分布对比。综合时变下的驱替效果是渗透率、原油黏度与相渗曲线时变共同作用的结果。在多种时变综合影响下,目标区块整体开发效果转好,但变化不明显。考虑综合时变模型的波及范围与洗油能力略强,近井周围波及范围较广且剩余油饱和度较低,但底部优势水淹层洗油能力略差,剩余油饱和度略高。

4 矿场应用

4.1 油田简介

B油田为断块圈闭构造的岩性构造油气藏,存在一定的边底水能量,但天然能量有限。该油田属于中高孔渗储层,沉积类型为三角洲沉积。目标油田储层埋深较浅,油层厚度约为23 m,流体性质较好,属于中质常规油,地饱压差较小。该油田采用定向井结合水平井的面积井网,为保持地层压力水平以注水开发为主。全油田采油速度约为2%,采收率35%,目前已处于高含水期。

4.2 不考虑时变的拟合效果

目标区块B油田存在一定的边水能量但能量大小无法准确描述,现场实际模型采用定油生产,再拟合含水率和累积产液量。

图9为ECLIPSE的含水率与累积产液量拟合结果,根据实际拟合效果,拟合精度仅为84.69%,且全区含水率整体偏高,在油田开发后期尤为明显,这是因为注入水的长期冲刷,储层物性较初期已有很大改变。长期注水改变了岩石的润湿性,降低了残余油饱和度,增加束缚水饱和度,进而造成油相流动能力增强,水相流动能力降低。此外,累积产液量后期也明显偏高,该现象是因为含水率较高,且生产井定油生产,造成产水量偏高,累积产液量越到后期与实际差距越大。拟合误差将严重影响生产指标预测,同时干扰剩余油分布的准确模拟。

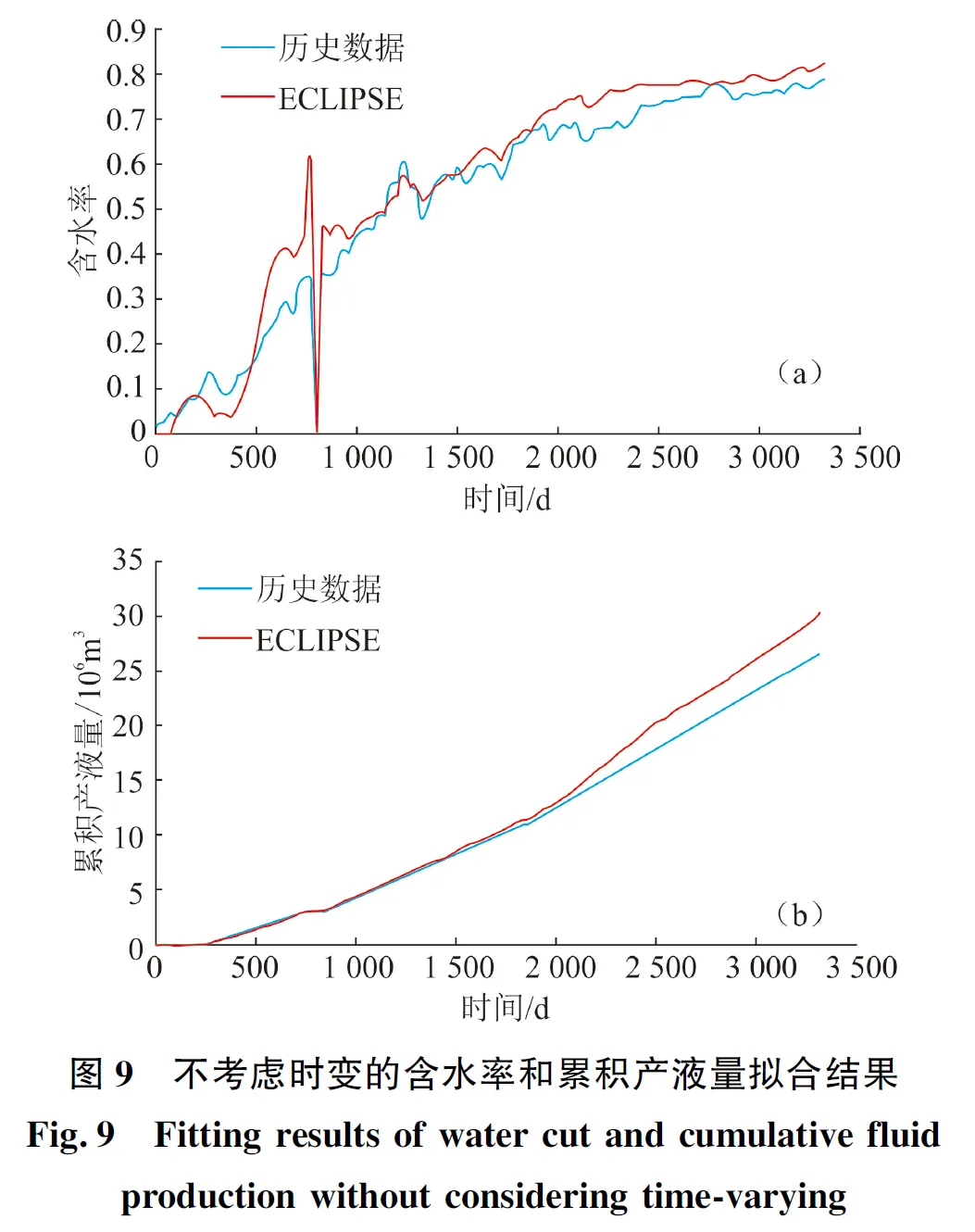
4.3 考虑时变的拟合效果

为进一步提高拟合精度和剩余油分布预测的准确性,在模拟过程中考虑储层物性时变的影响。由于矿场情况复杂,不同驱替通量下各时变参数的变化倍数以实际试验数据和前文总结得出的规律为基础,再进行人为调校。

通过对各时变参数进行多次调整,不断改善B油田实际模型拟合效果,最终各时变参数变化倍数与驱替通量间的关系如表1所示,目标油田全区含水率和累积产液量拟合结果如图10所示。含水率和累积产液量曲线的拟合效果显著提高,曲线整体基本重合,拟合精度高达91.53%,模拟结果更加可靠,剩余油模拟结果也更准确,为后期剩余油的表征评价和深度挖潜奠定基础。

表1 时变参数变化倍数与驱替通量之间的关系

5 结 论

(1)针对油田注水开发高含水期的客观规律,提出有效驱替通量的概念用以刻画水驱强度,克服了当前表征方法的缺陷,并结合矿产资料和试验数据拟合得出渗透率、黏度、相渗曲线特征参数变化倍数和有效驱替通量之间的函数式。

(2)考虑渗透率时变会使渗透率随注入水的冲刷变大,注水沿底部优势水淹层窜进,开发效果变差;原油黏度时变使水油流度比降低,造成水的黏性指进,波及系数和洗油效率降低,开发效果也变差;考虑相渗曲线时变后随着驱替通量的改变相渗曲线向右偏移,水相渗流能力降低,油相渗流能力升高,有利于驱油;综合时变是各时变参数共同作用的结果,其开发效果整体趋好。

(3)将时变数值模拟技术应用于B油田,其含水率和累积产液量的拟合效果较不考虑时变时有明显改善,预测剩余油分布更加准确。