形状的全尺度可视化表示与识别

闵睿朋，李一凡，黄瑶，杨剑宇*，钟宝江

1.苏州大学轨道交通学院, 苏州 215100； 2.苏州大学计算机科学与技术学院, 苏州 215100

0 引 言

视觉目标的形状是分析和理解该目标的重要依据，在目标识别、目标跟踪、图像检索和医学影响分析等领域具有广泛应用价值(周瑜 等，2012；毕威 等，2017)。因此形状特征的提取与表达一直是视觉领域的重要问题。例如在安检系统中，对伪彩色X光照片大多仅通过形状来判断是否含危险品；在医学影像中大多以形状作为诊断依据。虽然由于深度传感器等硬件设备的进步，物体的3维信息更容易获取，但是传统相机仍然是使用最广泛的视觉采集设备，对2维形状的分析和识别仍然具有重要价值。形状特征的提取与表达的结果对后续的识别分类非常重要，尤其是特征对不同类形状的区分度，以及对各种变换和噪声的鲁棒性。随着大数据的获取与应用日益广泛，深度学习模型体现出强大的学习能力。探索适合深度网络的高效特征表达方法，能够有效利用深度学习模型的学习能力，提高识别效果。

现有方法大多基于形状轮廓的位置关系和几何特征。经典的形状上下文(Belongie等，2002；Bai等，2010)方法及其改进方法IDSC(inner-distance shape context)(Ling和Jacobs，2007)利用轮廓点之间的位置关系。CCS(class segment sets)(Sun和Super，2005)等方法利用曲线几何特征，如曲率等。近年来，基于不同的形状上下文特征出现了一系列的形状表达和匹配方法(刘望舒 等，2017；Zhu等，2021)。Height function(Wang等，2012)利用轮廓点之间的距离关系取得了不错的效果。基于轮廓层次特征的方法从不同尺度获得轮廓特征(徐浩然 等，2017)。贾棋等人(2018)基于曲率分级对形状编码，获得不错的识别效果。但是这些方法获取的形状特征多为一系列离散轮廓点各自的独立特征数据，形成一组特征序列，从而轮廓起点的选取对特征表达的影响较大。尤其是有些方法需要在采样点对齐的前提下才能实现较好的特征匹配(Belongie等，2002；Ling和Jacobs，2007)，这在实际应用中较难实现。在识别阶段也多为使用动态规划等序列匹配方法(Müller，2007)，在训练数据量大的情况下运算效率较低。目前常用的深度学习模型如卷积神经网络(convolutional neural network，CNN)等方法的学习效率较高，而且适用于大数据应用，但以上这些形状特征表征方式不适用于深度学习网络模型。实验表明，直接将形状图像输入CNN模型进行分类的效果并不理想(Lee等，2017；Yang等，2017)。因此，亟待提出一种能够适用于深度学习模型的高效的形状特征表达方法以及相应的形状分类和检索方法，以适应在日益广泛的视觉大数据中的应用。

形状轮廓在二值化图像中仅是一条曲线，具有的信息量有限，对CNN网络来说，不足以获取足够的形状特征。因此直接使用二值化图像训练CNN模型进行分类无法获得较高的精度。为了能够充分利用CNN模型的学习能力，最关键的问题是如何充分提取形状特征并以图像的形式充分表达出来，从而供CNN模型进行特征学习以更好地完成分类任务。

本文提出一种新的形状特征提取和表示方法，通过充分提取形状轮廓的全部尺度的特征，并紧凑地将全部特征表示在单幅彩色图像上，形成一种全尺度单彩图形状表示方法，适用于深度卷积模型来完成分类任务。流程如图1所示。首先使用自适应离散轮廓演化(adaptive discrete contour evolution，ADCE)算法提取形状轮廓的显著特征点，接着使用多尺度不变量(Yang 等，2016)提取形状特征，然后将该描述扩展到整个尺度空间，获得全部离散尺度的特征表达，再将3种不同描述结果分别用RGB图像的3个通道进行色彩表达，获得一幅RGB图像，并以形状原图作为参考图像，一起输入本文设计的双流CNN网络进行训练，以达到形状识别的目的。

本文提出的单图表示方法可将形状特征进行彩色可视化，从图像上直观反映形状的相似性和不变性。从形状轮廓提取的全尺度特征能够充分获取形状的各方面特征信息。本文方法不需要将形状轮廓起点对齐，可以使用任意起点，从而简化步骤，提高精度，并扩大应用范围，具有较高的鲁棒性，可适应形状的多种几何变换与不同程度的噪声干扰。

1 全尺度形状描述子

1.1 多尺度形状描述子

在2D形状检索和分类任务中，原始的形状数据是由形状轮廓上一系列采样点组成的闭合曲线S，定义为S={p(i)|i∈[1,N]}，其中N为轮廓采样点的总个数,p(i)为第i个采样点。在形状匹配任务中，一种常用的方法是设计形状描述子来提取采样点处的形状特征信息。其中多尺度形状描述子(Yang等，2016)能够提取较为丰富的形状特征，且不同特征之间具有互补作用。该描述子使用归一化面积s、归一化弧长l和归一化重心距c等特征，并分别在半径逐次减半的多个离散尺度q∈[1,Q]上提取形状特征，其中Q为总尺度个数。因此获取的多尺度描述为

M={sq(i),lq(i),cq(i)|i∈[1,N],q∈[1,Q]}

(1)

式中，sq，lq和cq的定义为

(2)

(3)

(4)

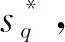
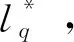
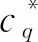
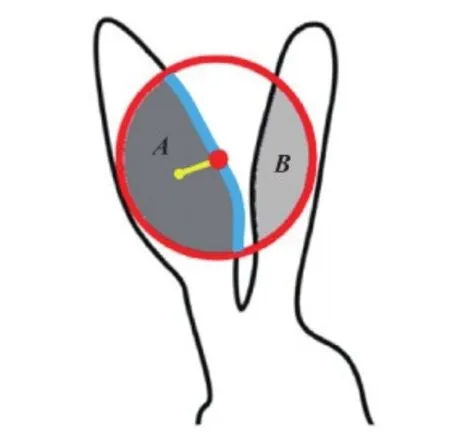
图2 形状描述子计算区域示意图Fig.2 Calculation area of shape descriptor

在特定的尺度q下，特征圆Cq(i)的半径rq定义为

(5)

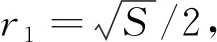
虽然该方法中3个多尺度描述子可以分别从0维、1维和2维3个方面提取从全局到局部的形状特征，但是存在以下几个问题：

1)使用多尺度描述子计算出的特征函数集较大，每个形状需要3×Q个函数曲线来抽象地表达，如图3(b)所示，对形状特征不易可视化。

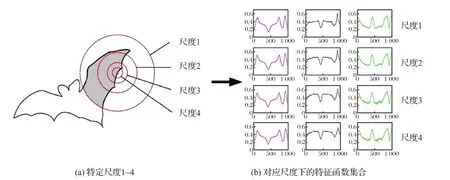
图3 多尺度形状描述子的形状特征表达Fig.3 Shape representation with multi-scale shape descriptors ((a) certain scale 1 4；(b) the feature functions at the corresponding scale)

2)特征圆半径rq以2的指数倍变化，忽略了大尺度特征的变化情况，默认特征细节随着尺度增大而减少，而且只能提取特定离散尺度下的部分信息，丢失了尺度空间中的大部分特征信息。

3)提取的描述子中，每个轮廓点的特征是独立的，没有表达出轮廓点之间以及不同尺度之间的特征关系。由于使用动态规划等点匹配算法，轮廓点之间和不同尺度之间的特征关系也未能用于识别和检索。

4)使用动态规划算法进行抽样点对应匹配计算量较大，不适合大数据量的分类和检索任务。

本文提出的形状表示方法旨在克服上述缺点，提高形状特征的提取和表达能力，以适应深度学习模型，利用其学习能力更好地完成检索和识别任务。

1.2 全尺度空间形状描述子

为了提取形状特征在所有尺度上的特征信息，本文方法在整个尺度空间对描述子进行连续采样。因为描述子的尺度变量是特征圆半径rq，将其取值设为rq∈(0,R)，即从0到半全局半径R之间的全部数值。由于数字图像是离散采样，以像素为最小单位，故选择rq取(0,R)区间内的全部整数值。r1=1为第1个尺度，因此，尺度q下的特征圆Cq(i)的半径rq为

rq=q,q∈[1,R),q∈N

(6)

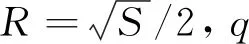
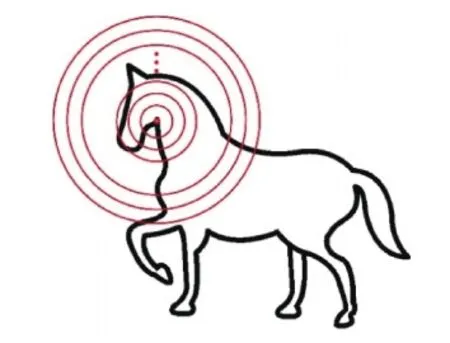
图4 全尺度表达的特征圆Fig.4 Feature circles of all the scales

1.3 显著特征点的提取

在计算全尺度空间形状描述子时，若形状轮廓的所有点都参与计算，会使得许多没有显著特征的冗余点与显著特征点有相同的权重。这会削弱描述子的表达能力，而且冗余点的存在会大幅增加计算成本。因此，有必要去掉形状轮廓中的冗余点。

为了提取轮廓的显著特征点，Latecki等人(2000)提出了离散轮廓演化(discrete contour evolution，DCE)算法。但是这一方法不能自适应地演化至收敛。因此，本文使用自适应离散轮廓演化(adaptive discrete contour evolution，ADCE)算法(Yang 等，2016)，该算法引入了一个基于区域的自适应结束函数，当该函数值超过设定阈值后，轮廓显著特征点提取结束。需要注意的是，ADCE步骤只是用来找到具有代表性的特征点，计算全尺度空间形状描述子还是通过原始形状轮廓进行计算。这样做的目的是保留显著特征点的原始形状特征。

2 形状的图像表示

如前所述，使用多尺度描述子计算出的特征函数集较大，形状特征不易可视化，且轮廓点之间和不同尺度下的形状特征关系未能利用。因此，本文提出一种紧凑的彩色图像表示方法，用一幅彩色图像表示整个形状在所有尺度下的不变量特征。

2.1 单尺度形状描述子的图像表示

在单一尺度q下，对所有轮廓采样点{p(i)}计算不变量描述子，获取对应的3种形状不变量特征{sq(i),lq(i),cq(i)|i∈[1,N]}。3种特征可以分别表示为特征函数，如图5(b)所示，其中横轴为轮廓点序列，纵轴为描述子数值。将这3个特征函数的取值记入3个大小为1×n的特征矩阵，并进行灰度归一化显示，如图5(c)所示，3个大小为1×n的灰度图分别表达对应的特征函数包含的形状信息。将这3个灰度图分别取色R、G和B，即可表示为3幅单色图像。

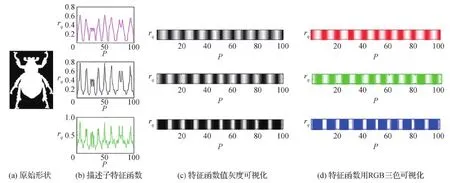
图5 特征函数的彩色表达Fig.5 Color representation of feature functions ((a) original shape image; (b) feature functions of descriptor; (c) visualization of the feature functions with gray degrees; (d) visualization of the feature functions with RGB)

2.2 全尺度形状描述子的图像表示

由上一小节可知，在单一尺度下，特征图像能够取代特征函数曲线表示该尺度下的形状特征信息。以此类推，对于全尺度空间下所有尺度q∈[1,Q]，其不变量描述函数可以表示为Q个大小为1×n的特征矩阵。将这Q个特征矩阵按照尺度连续变化的顺序合并，即构成3个尺寸为Q×n的特征图。如图6所示，这3个单色特征图能够紧凑地表示出描述子在所有尺度下提取出的全部形状特征信息。

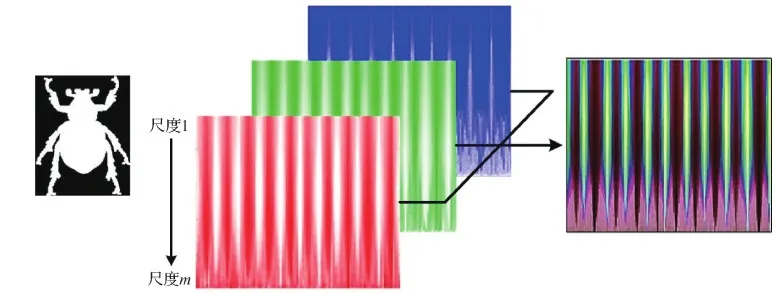
图6 形状的彩色表达图Fig.6 Color representation of shape

2.3 全尺度形状描述子的彩图表示

将上述3个单色特征图作为R、G、B这3个通道合成一幅彩色特征表达图像I，即可更加紧凑地用一幅图像表示形状的全部特征。如图6所示，示例形状的RGB表示图不仅同时包含了全尺度空间描述子提取的所有形状特征，而且直观地实现了原始形状的特征可视化。在该彩色图像表示中，不同尺度和相邻轮廓点的形状特征之间的关系，在图像中皆以邻接像素(x轴为相邻轮廓点，y轴为相邻尺度)体现。卷积神经网络能够有效学习相邻像素之间的关系，即可以学习到相邻轮廓点之间的形状特征关系、相邻尺度之间的特征变化关系以及3类形状特征描述子之间的互补关系，从而可以利用深度卷积模型来学习形状特征，并完成分类和检索等任务。

3 形状分类与检索

本文方法将形状表示成一幅RGB图像，该图像能够同时包含原始形状在全尺度空间下的多个不变量形状特征信息，因此可将其作为形状分类的依据。此外，由于本文方法将轮廓形状转换为张量表达，尤其适合利用卷积神经网络(CNN)强大的图像特征抓取和表达能力，从而提高识别和检索精度，所以本文选择构造CNN框架来实现分类任务。首先微调VGG16(Visual Geometry Group 16-layer net)网络结构对特征表达图像I进行分类。在其连续卷积的计算过程中，既能够提取各显著点在全尺度空间中的特征，又能够同时抓取相邻显著点之间的特征关系。相比以往方法将对应轮廓点的形状特征序列进行匹配计算形状间的特征距离，本文方法能够更加全面地分析形状所包含的信息。

虽然该彩色图像表示具有丰富的多层次信息，但其表示的形状特征信息是原始形状特征投影到不变量空间和尺度空间的结果的可视化，这在图像层面较为抽象。再经过多层卷积神经网络进行特征提取后，得到的特征为该投影图像的深度特征，与原始形状轮廓图像的直观几何特征之间差距很大，并有可能在训练过程中造成梯度消失等问题，对形状分析和识别任务增加难度。受ResNet启发，本文在将彩色特征图I输入CNN模型的同时，将形状轮廓的原始图像S作为辅助信息直接输入VGG16网络，以获取更加直接的形状几何特征，从而形成两路CNN结构。然后将两个CNN模块的输出特征一起输入全连接层进行识别。

在检索任务中，本文使用从CNN模块输入全连接层的特征矢量作为检索特征，计算不同形状的检索特征矢量之间的欧氏距离作为形状之间的差异大小，并依据Bull-eye(Latecki等，2000)标准计算检索结果。

4 实验结果

实验从3方面验证本文方法。首先验证本文提出的形状表示方法对刚体变化具有不变性，包括旋转和缩放变换。然后验证本文形状表示方法对类内变化、铰接变换、部分遮挡和噪声干扰的鲁棒性。此外，在几个重要的形状数据集上进行形状分类和检索，包括MPEG-7(Latecki等，2000)数据集、Animal(Bai等，2009)数据集和铰接(Ling和Jacobs，2007)数据集等，并将本文方法的实验结果在相同条件下与对比方法(Zheng等，2019；Shen等，2018)进行比较。

4.1 形状表示的不变性

实验首先验证本文提出的形状表示方法对形状图像旋转和缩放变换得到的表示结果的不变性。本文将原始形状图像分别进行这两种变换，然后分别计算得到彩色特征表示图，并与原始形状图像的彩色特征表示图进行对比，如图7所示。图7(a)(b)分别为形状图像及进行旋转和缩放对应的特征表示图。从特征表示图可见，原始形状和对应的旋转或缩放后的形状特征图相同，验证了本文的表示方法对旋转和缩放这两种刚体变换具有不变性。

4.2 形状表示的鲁棒性

同类物体的形状往往具有较大的类内变化，使得提取的形状特征往往具有较大差异，给形状识别和检索带来困难。如图8所示，各列为同类的形状。从对应的特征图可以看出，同类的形状虽然具有较大差异，但是仍然具有相似的特征图(马匹的特征图也是对称的)，从而降低了类内差异对形状识别和检索任务的影响。

铰接变换是一种典型的类内差异，如图9所示，图9(a)两个鹿的形状分别为站立和奔跑姿势，两者的腿部之间具有显著的铰接变换关系。类似的情况还有人的手指、物品中的剪刀等，都会对形状识别任务造成困难。为此，Ling和Jacobs(2007)提出一个铰接数据集专门用来测试铰接变换下的形状识别精度。从图9(a)鹿形状的特征图可以看出，红色框内的铰接部分形状对应的特征具有很高的相似度，说明本文的表示方法在铰接变换下具有鲁棒性。

除了类内差异，在形状分析的实际应用中，还会遇到部分目标遮挡的情况。如图9(b)所示，第2行马匹形状的头部被遮挡，将会对识别分析造成影响。从对应的特征图可以看出，除了红色框内部与马匹头部对应的形状特征图外，其他部分完全一致，验证了本文特征表示方法对形状部分遮挡情况的鲁棒性。

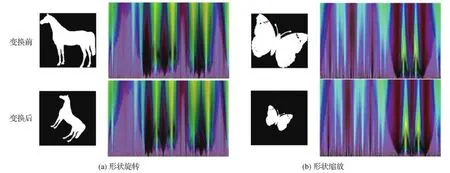
图7 形状的旋转和缩放变换前后的特征图表示Fig.7 Feature map of shapes before and after rotation and scaling((a)rotation;(b)scaling)

图8 类内差异形状的特征图表示Fig.8 Feature map of shapes with intra-class variations((a)bat;(b)beetle;(c)horse)

图9 铰接变换、部分遮挡和噪声干扰下的特征图表示Fig.9 Feature map of shapes with articulation, partial occlusion and noise ((a)articulated variation;(b)partial occlusion;(c)noisy disturbance)

因此在实际应用中，仍然可以利用未遮挡部分的形状信息进行识别。

噪声干扰对图像识别同样具有影响，如图9(c)所示，第2行的形状为第1行形状加入噪声后的形状。从两个形状对应的两幅特征图可见，其特征图像相似度很高，几乎不受到噪声的影响，从而验证了该表示方法对噪声的鲁棒性。

4.3 形状分类与检索

使用MPEG-7(Latecki 等，2000)数据集、Animal(Bai 等，2009)数据集、铰接(Ling和Jacobs，2007)数据集和PLD(projective landmarks database)(Bryner等，2014)射影变换数据集对本文方法的分类和检索精度分别进行测试，并与其他模型方法进行比较，以验证本文方法的效果。

4.3.1 实验设置

对于形状数据，在轮廓上统一采样100个轮廓点，并设置尺度空间总尺度数为100，从而得到100×100像素的特征表达图像。同时，将原始轮廓形状尺寸归一化为100×100像素。将原始形状及其对应特征表达图像二者同时输入双路卷积神经网络结构模型中进行训练。实验网络选择SGD(stochastic gradient descent)优化器，学习率设置为0.001，延迟率设置为1E-6，损失函数选用交叉熵，双流特征权重设为1 ∶1，分类器选择softmax。实验中将模型训练100个epoch，每个epoch中batch size大小选择为128。

在训练过程中引入VGG16模型在ImageNet数据集中训练所得参数作为预训练，解锁VGG16模型中最后3个全连接层进行训练并根据收敛速率进行参数微调。在形状分类和检索时，在MPEG-7和Animal数据集上分别使用一半训练一半测试及留一法两种测试方法。一半训练一半测试即将目标数据集中每一类形状随机平分为两个子集，一半用于训练，另一半用来测试，执行10次后计算准确率的平均值；留一法即将数据集中每一个形状分别作为一次测试集，其余形状全部作为训练集。

4.3.2 MPEG-7数据集

MPEG-7(Latecki等，2000)数据集是最为广泛用来进行形状匹配与形状检索任务的公开数据集，共1 400个不同的形状样本，分为70个形状类别，每个类别包含20个形状样本。部分形状样本如图10所示，包含每个类别的2个代表形状。

图10 MPEG-7数据集形状示例Fig.10 Example shapes of MPEG-7 dataset

本文方法在MPEG-7数据集中的分类准确率与其他典型方法的对比结果如表1中第2列所示。该分类结果为采用一半训练一半测试方式的分类精度，本文方法取得了99.09%的分类准确率，超过了目前最新方法的分类精度，达到目前最高准确率。

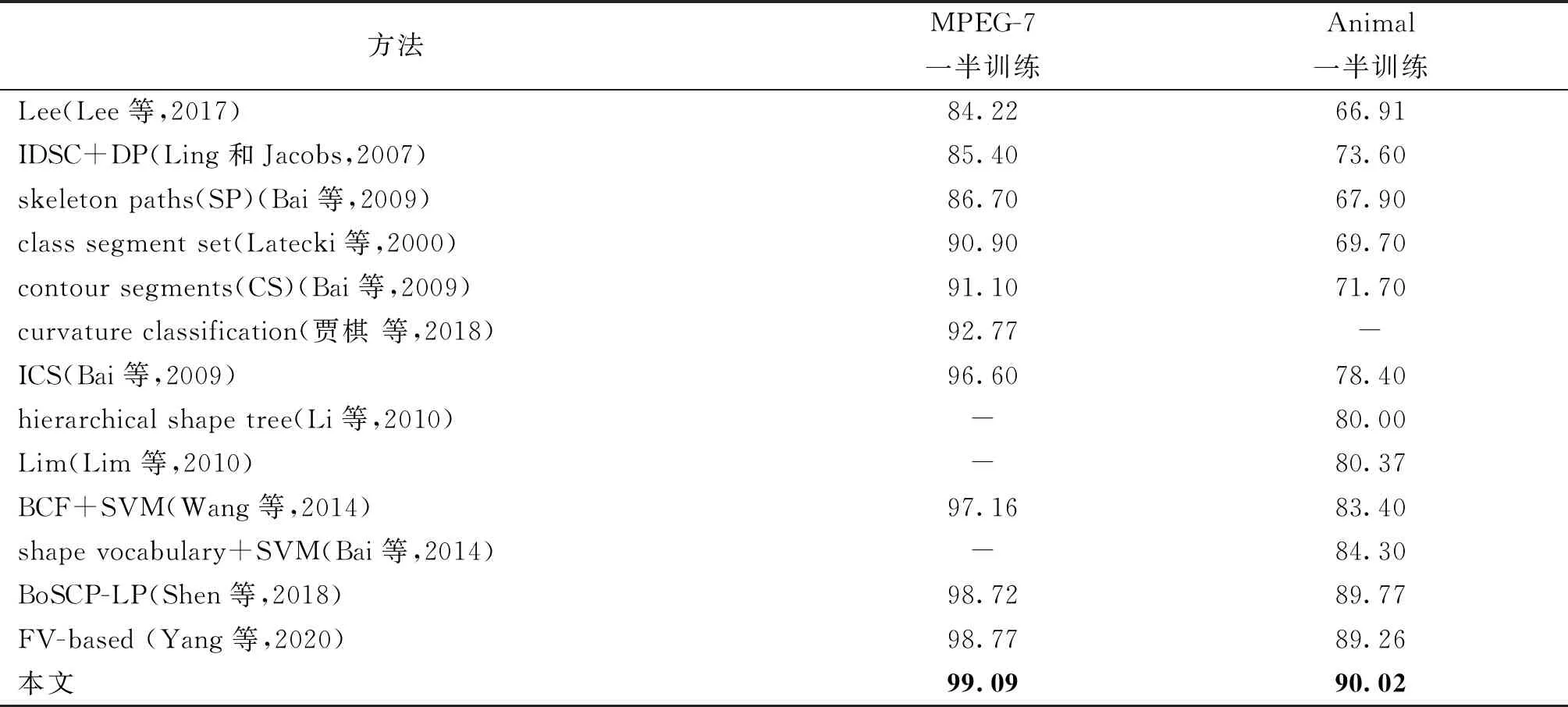
表1 不同方法在MPEG-7和Animal数据集的分类准确率对比Table 1 Comparison of classification accuracy on MPEG-7 and Animal datasets among different methods /%

在形状检索实验中，采用Bull-eye准则计算检索准确率。本文方法在MPEG-7数据集中的检索准确率与对比方法结果如表2的第2、3列所示，分别为一半训练一半测试方式和留一法的结果。可以看出，本文方法在两种测试方式中分别获得了99.14%和99.57%的检索精度，超过了所有其他方法。

由此可见，本文方法与传统形状描述子相比，在尺度空间下更全面地提取了形状轮廓的特征信息，而且特征图表示法利用了卷积神经网络对图像特征的学习能力，充分学习了数据集中的形状特征，从而获得了出色的形状分类和检索精度。

4.3.3 Animal数据集

Animal(Bai等，2009)数据集由2 000个不同的动物轮廓作为形状样本构成，包含20个不同的动物种类，每个动物种类有100个动物形状样本。在每一类动物中，100个形状样本具有显著的形状变化，对分类和检索任务增加了较大难度。图11展示了每个动物类别中的6个代表形状，从中不难发现同类动物的轮廓形状之间具有很大差异，这一类内变化对于分类和检索任务来说具有更高难度。本文方法和对比方法在该数据集中测试得到的分类结果如表1第3列所示，本文方法获得了90.02%的分类正确率。相比于其他方法，本文方法取得了最高分类准确率。

表2第4列列出了在Animal数据集中进行形状检索的准确率，该结果同样使用Bull-eye准则。从表中结果可见，其他方法在Animal数据集上的检索准确率都不高，说明该数据集对于检索任务具有较高难度。而本文方法获得了90.75%的检索准确率，超过其他方法最好结果24%，说明本文方法对于各种类内变化具有较好的鲁棒性，对于类内变化较大的数据集仍具有很强的检索能力。

4.3.4 铰接形状数据集

铰接变换是一种常见的类内变化，对形状分类和检索等任务造成困难。为了测试形状识别和检索方法针对形状发生铰接变换时的鲁棒性，Ling等人(2007)采集了一个铰接形状数据集，共40个样本，分别属于8个不同物体，每个物体采集5种不同的铰接变换姿态，数据集的形状都是剪刀、折叠刀等具在该数据集上进行检索实验，并与其他方法进行对比，结果如表3所示。可以看出，本文算法进行形状检索的准确率为100%，超过其他方法10%以上。由此可见，本文方法对形状的铰接变换具有很好的鲁棒性。

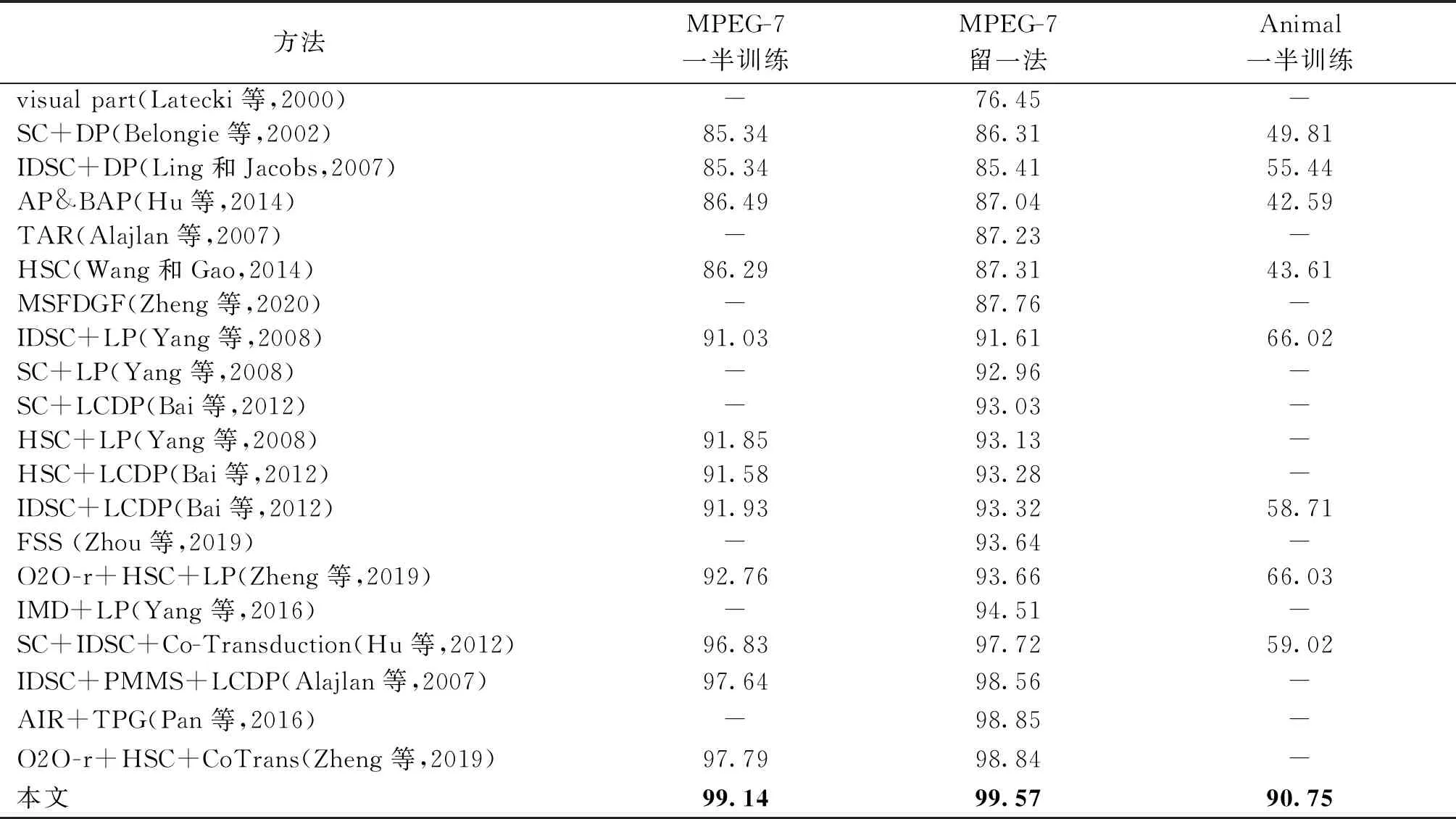
表2 不同方法在MPEG-7和Animal数据集的检索准确率对比Table 2 Comparison of retrieval accuracy on MPEG-7 and Animal datasets among different methods /%

图11 Animal数据集形状示例Fig.11 Example shapes of Animal dataset

有较大幅度的铰接变换的物体形状，对算法的鲁棒性要求很高，如图12所示。

图12 铰接形状数据集样本图Fig.12 Shapes of articulated dataset

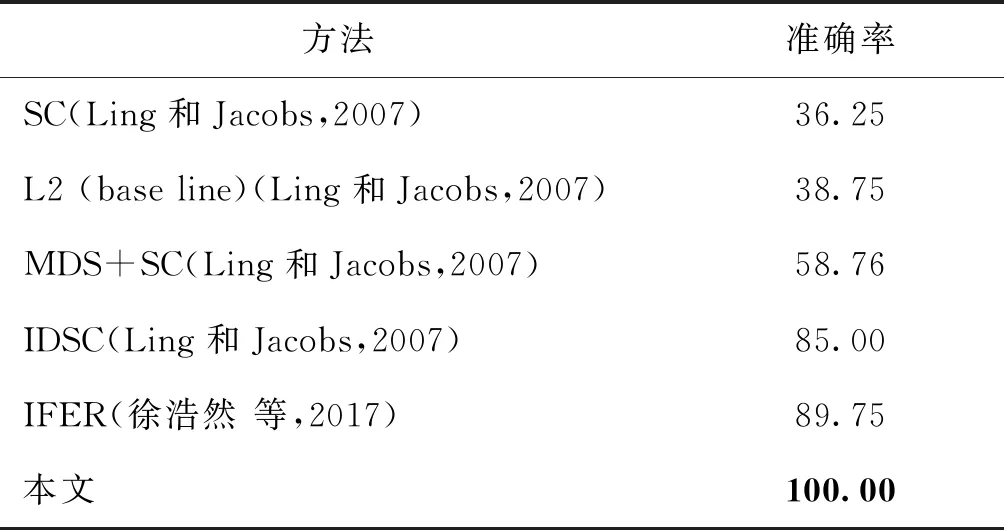
表3 铰接形状数据集检索准确率Table 3 Retrieval results on articulated dataset /%

4.3.5 PLD数据集

在实际的图像采集中，常常因为拍摄的视角问题，在图像中呈现目标的不同角度的投影，从而造成同一目标得到不同的形状轮廓。不同轮廓之间的变化称为形状的射影变换。较为显著的射影变换会使形状分类和检索精度受到影响。PLD数据集中的样本具有显著的射影变换，专门用来测试形状分类和检索方法在射影变换下的鲁棒性，如图13所示。该数据集由100个形状组成，包含MPEG-7数据集中的10类不同形状，有9种不同的射影变换，样本与原始样本之间具有明显的射影形变。

图13 射影变换形状数据集样本图Fig.13 Shapes of projective dataset

本文方法使用PLD数据集进行形状分类时取得了100%的准确率，与其他方法的对比结果如表4所示。表4第2、3列分别为一半训练一半测试方式和留一法训练的分类结果。本文方法在两种训练方式中都将全部形状正确分类，说明在射影变换中具有很好的鲁棒性，可以适应实际应用中的复杂投影情况。

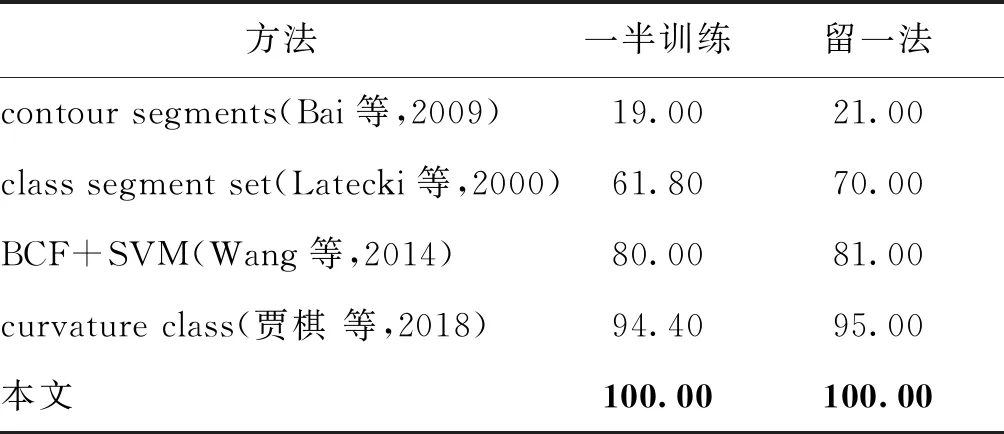
表4 PLD数据集分类准确率Table 4 Classification results on PLD dataset /%

5 结 论

本文提出一种单幅彩色图像的全尺度形状表示方法，以及相应的基于深度学习的形状分类和检索方法。该方法在整个尺度空间全面提取目标轮廓的形状特征，并紧凑地进行图像可视化特征表达，适合深度学习模型，并适用于大数据环境，同时对各种图像干扰具有鲁棒性，在干扰情况下仍能获得较高的识别和检索精度。但在Animal数据集上的实验精度存在一定的错误率，主要是因为动物身体多为软体而非刚体，因此形变较大且无规律，使得在部分样本中能够捕捉的特征有限。

本文方法主要针对2维形状的轮廓特征进行分析，未开展面向3维形状的特征分析与识别。随着3维图像采集系统的广泛使用，3维目标的形状信息获取变得更加容易。相对于2维的目标轮廓，目标的3维形状包含更加丰富的信息。因此，今后将分析本文方法在面向3维形状特征时遇到的问题，进一步研究3维形状的特征表示与识别方法，提高表示、分类和检索能力。