单目相机轨迹的真实尺度恢复

刘思博，房立金

1.东北大学信息科学与工程学院， 沈阳 110819； 2.东北大学机器人科学与工程学院， 沈阳 110169

0 引 言

相机的运动轨迹恢复也称为视觉里程计(visual odometry，VO)，主要是将单目或双目相机拍摄的图像还原出整个相机的运动过程轨迹，从而进行精准定位与建图。然而相机轨迹的恢复一直伴随着尺度问题，因为单目相机先天性缺乏尺度信息，只能获得像素点之间的远近关系。为了得到准确的相机运动轨迹，需要获得图像中每个像素点对应在3维空间中的深度值，主要采用直接使用带有深度的传感器和使用神经网络学习后进行估计两种方法。

3D LIDAR(light detection and ranging)传感器是最精准的测距传感器设备，大部分数据集的真实深度信息都是LIDAR采集得到，但其造价昂贵且获得的是稀疏深度，不容易普及。以RGB-D相机为主的利用time-of-light的深度传感器，虽然能够直接对深度进行测量，但容易受噪声和物体结构影响，特别是在透明、强反射或者表面较暗的地方，一般只在室内使用。使用立体图像对(双目相机)同样可以计算深度，原理是测量同一像素在一对图像间的视差，再依据立体几何关系对深度进行计算，但计算量大且光心之间的基线变化会严重影响测量范围，不方便迁移应用。

基于神经网络对单幅图像进行相对深度估计的方法已逐渐成熟，根据是否直接使用数据集进行训练分为监督学习和自监督学习。监督学习通过直接寻找图像信息与真实深度值的关系进行端到端训练来获得最合适的模型(Eigen等，2014)，虽然误差明显降低，但最大缺点是训练所需的真实数据标签难以获得且成本较高。

自监督学习是对2维图像像素点之间的内在约束关系(如这些点在3维空间中的几何关系)进行学习。使用标定过的双目立体图像对训练的方法(Garg等，2016)利用网络学习图像对之间的视差值还原另一侧图像后，将其与真实图像的光度差作为监督信号进行训练，但双目相机由于基线距离的变化会导致深度值尺度不一致，不同相机间不能迁移使用。融合自运动估计网络的方法(Zhou等，2017)通过对单目视频序列间的相机运动进行估计，并利用位姿变换合成出的图像与真实图像的光度差作为损失进行训练。虽然利用得到的位姿成功约束了像素点对应的空间几何关系，但提出的PoseNet对于位姿的估计误差较大，精度不足以进行实际应用。DDVO(differentiable direct visual odometry)(Wang,2018)方法认为Zhou等人(2017)方法没有充分利用摄像机姿态和深度预测之间的关系，于是引入一个直接视觉测距(DVO)位姿预测器，并在此基础上进行可微处理得到DDVO模块，将姿态估计结果传回深度估计模块实现端到端处理，但其对动态环境和开阔场景效果不好。基于运动模型的方法(Casser等，2019)通过分析3维几何结构，在动态场景中分割出运动物体，与预定义物体进行匹配，根据给定高度恢复尺度。但场景中不存在预训练模型中的物体时无法进行应用，且由于物体尺寸不统一，计算的尺度结果也不稳定。目前效果最稳定的深度估计方法(Godard等，2019)采用编码—解码结构，在提取图像特征后对深度和位姿同时求解，利用连续帧间的变换关系进行最小重投影误差计算，解决了遮挡和低纹理区造成的偏差，并设计自运动掩膜检测出同速移动的运动物体，深度和位姿的精度都得到提高，但仍然仅估计了相对深度而没有计算尺度信息。

在比较单目和双目等方法后发现，对于深度的计算，引入额外的传感器虽然精度得到提高但相对需要添加校正和初始化过程，增加了实验的复杂性，并且很难进行普及应用。使用单目的方法则能够快速、稳定地计算深度信息，并且单目设备的获取与初始化过程更简单。本文提出引入先验条件的方法，使用深度网络和光流网络计算连续图像的相对深度图及相邻图像间的高匹配特征点，利用场景几何约束恢复真实尺度，从而得到绝对深度值和真实相机运动轨迹。

1 尺度恢复算法

单目深度估计以及相机运动轨迹由于仅使用单个相机采集的数据进行计算，无法获得准确的尺度信息。目前的高精度深度估计算法，如最小化重投影差(Godard等，2019)、尺度一致性约束(Bian等，2019)、同时学习深度光流与相机运动(Ranjan等，2019)、利用结构与语义学习深度和自运动(Casser等，2019)、分层结构求取绝对深度(Xue等，2020)等，在相对深度图中能够明确分割物体轮廓与深度细节，得到的深度图也更加平滑。但仅知道像素点间的远近关系不能进行实际应用，为此引入先验条件利用像素点间的结构关系进行真实尺度计算，在相对深度图转换为绝对深度的同时，对相机运动轨迹中的偏移量尺度进行恢复。

本文同样采用单目视频序列作为输入，步骤如下：

1)对连续帧图像经过深度估计网络进行相对深度计算。

2)利用估计出的相对深度值将图像中的2维像素点投影到3维空间，对整个3维点云进行表面法向量计算。

3)经过阈值筛选得到法向量垂直的地面点群，对所有地面点进行相机高度计算后，与相机先验高度求比作为初始尺度SGround。

4)为减小图像噪声造成的尺度误差，引入检测网络在检测到目标物体时计算补偿尺度SCar对初始尺度SGround进行补偿后作为最终尺度S，进而得到绝对深度图。

5)相机运动轨迹通过对连续帧图像进行光流估计，利用前后向光流一致性找出匹配度最高的有效点，并使用传统方法求解本质矩阵E，通过对E进行分解得到相机位姿中的平移量t和旋转量R。

6)当相机有明显运动情况时，直接利用对极几何求解位姿后进行尺度恢复。如果运动过小，利用前一帧带有相对深度的3维特征点与后一帧匹配到的2维像素点进行求解再进行尺度恢复，完成对深度和相对位姿的尺度恢复，如图1所示。

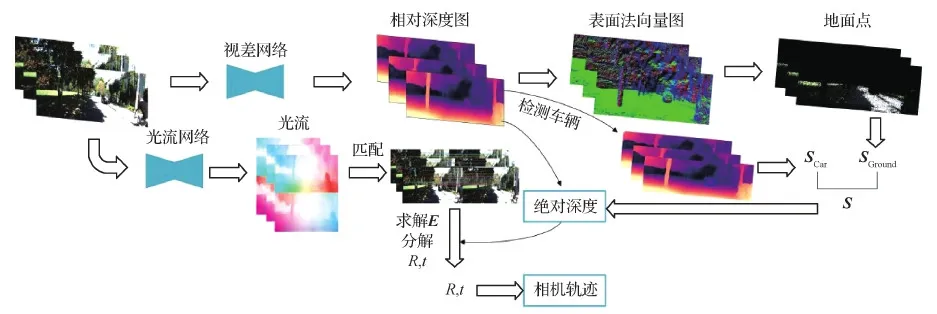
图1 算法流程图Fig.1 Algorithm flowchart

本文算法相比于之前的方法有3个优点：1)添加3维空间点云之间的重投影误差，对位姿与相对深度添加尺度约束；2)利用光流匹配特征点后，使用传统方法代替不稳定的位姿网络求解位姿；3)使用地面点群作为检测对象，防止算法因没有识别对象而失效。

2 计算真实尺度的相机位姿

相机位姿的真实尺度需要先进行相对深度值计算，利用深度关系找到像素点的空间结构进行尺度计算，再利用光流找到匹配点，使用传统方法求解位姿并进行尺度恢复。

2.1 利用图像信息获得深度

由于尺度的不确定性，使得同一像素点能够投影为多个深度，因此必须施加额外的约束条件训练网络，在找到像素点间相对深度关系的同时计算出准确的尺度信息。自监督训练利用图像间像素点的对应关系(空间立体几何)估计相机自身的位姿变换，并对相邻图像进行重投影操作，将减小合成图像与真实图像之间的光度差作为目标进行训练，整个过程没有使用真实深度值作为训练标签。

本文提出的深度估计模块与Godard等人(2019)方法相似，网络输入为单目视频序列，每次训练输入3帧连续图像以及标定过的相机内参。深度网络的目标是得到一个端到端的深度估计函数，在没有任何真实深度标签作为监督信号时，需要使用额外的6维位姿信息(tx,ty,tz,rx,ry,rz)(包括 3个位移项和3个旋转项)对相邻图像在空间进行重投影。首先通过内参和相对深度将图像投影到3维空间，具体为

Dij·K-1·[u,v,1]T=[x,y,z]

(1)

式中，[u,v,1]T为3维空间坐标[x,y,z]T对应的2维像素点，Dij为像素坐标(i,j)对应的深度值，K为相机内参。再利用外参T将3维点[x,y,z]T投影到相邻帧图像空间后，使用式(1)的逆变换重投影到新的像素平面。

[u′,v′,1]T∝K·T·[x,y,z]T

(2)

式中，[u′,v′,1]T为[u,v,1]T投影到相邻帧图像空间的像素坐标，如图2所示。

图2 重投影效果图Fig.2 Re-projection renderings((a)raw image;(b)previous frame;(c)next frame)

在获得重投影的像素坐标后，对原始图像进行双线性采样，使得图像局部可微，并将合成后的新图像I′a与真实图像Ia进行光度差计算，得到重投影损失PE，具体为

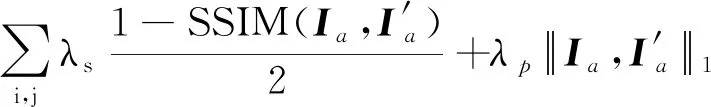
(3)

式中，采用L1范数防止数据的过拟合(Zhao等，2015)，而SSIM函数则有效对比两帧图像间的结构相似性(structural similarity index，SSIM)，且忽略光照变化的影响(Wang等，2004)，其中参数λp= 0.15，λs= 0.85。

但几何约束关系的成立有一个强约束条件，即场景中不存在任何移动物体，也就是整个背景是静止的。而对于现实世界的复杂场景来说，除了运动物体，还存在各种遮挡情况，这些都会使网络不能学习到真正有效的信息而影响效果。

对于输入为连续3帧图像的网络，当全部3帧图像稳定匹配时，连续图像的重投影误差均较小，不会影响训练目标函数。当仅有两帧图像正确匹配时，对于由于遮挡或动态因素造成的连续图像误匹配计算出的重投影误差会明显过大，而实际目标均为连续图像，与构造的损失函数的学习目标相差过大，错误的重投影误差很可能会导致训练最终无法达到网络效果。因此使用最小重投影差代替原先的平均重投影损失能够有效避免由误匹配造成网络对错误信息的学习。即

Lp=min[PE(It,Im)]

(4)

式中，Im由前后帧图像经过投影变换后的结果(It-1→t,It+1→t)以及前后帧原始图像(It-1,It+1)共4帧图像组成，Lp表示当前时刻It与Im之间的光度差的最小值。

此外，对于光度差的计算，直接进行叠加会使不准确的网络估计结果以及中间处理过程的偏差加入到后续训练过程，造成网络的学习效果不好，特别是在多尺度深度处理过程，由于低分辨率的结果在后续的上采样过程会重复叠加使用，误差也会累积放大，因此随着分辨率的增大，损失权重ωi呈指数形式增加，其中低分辨率的权重最小，具体为

(5)

式中，It,s,Im,s分别为在t和m时刻尺度因子为s的图像，s取值范围为1 4，对原图像长宽同时进行尺度缩放。

大多数方法都假设估计出的位姿以及深度之间的尺度是一致的(Zhou等，2017)，这样很容易造成视觉里程计的尺度偏移现象。为了加强位姿与深度之间的约束，通过将任意连续两帧图像的相对深度投影到对应3D空间，得到两个点云(Pa,Pb)，并计算空间变换后(Pa→b)两者的距离差，进行相对深度和位姿之间的尺度约束，具体为

(6)

式中，Ea→b为连续图像(Ia,Ib)之间的位姿变换(外参)。然而，对所有点直接进行几何损失训练出的深度估计结果在运动区域效果较差，且会影响周围的估计效果，这是由于在自动驾驶领域常常会出现人、车辆等运动物体，并且会在其对应变化区域产生遮挡现象而产生较大的重投影误差，这些区域对于学习来说大部分都为无效信息。因此，实际计算中以图像间重投影误差作为训练权重，当所在区域由于误匹配或遮挡造成较大误差时，视为无效信息而降低训练权重，反之亦然。

这种采用视图合成方法对连续图像进行重投影计算遮挡区域的方法同样被SC-SfM(scale consistent-structure from motion)(Bian 等,2019)方法所采用，其网络进行位姿估计，并将重投影差作为权重进行训练得到准确结果。GeoNet(deep geodesic networks)(Yin 和 Shi,2018)同样使用图像合成学习刚性流和物体运动来区分三维场景中的动态物体，但使用的是光流前后方向一致性过滤遮挡部分。与前面不同的是，SGDepth(semantically-guided depth estimation)(Klingner 等,2020)提出一种新的语义引导深度估计方法来处理动态运动问题。采用有监督的语义分割和自监督的深度估计进行互利跨域训练，对运动物体影响的光度损失进行语义遮蔽，并对刚体进行检测。

此外，由于光度差损失在重复纹理或均匀区域进行约束的影响效果不大，通过计算估计深度的边缘平滑度损失，使得学习出的深度结果纹理更加明显、平滑。具体为

(7)

2.2 光流求解位姿

真实相机运动轨迹的精确程度离不开准确的位姿估计。基于网络对连续图像直接进行位姿估计，虽然计算速度快、效果好(Zhou等，2018; Dharmasiri等，2018)，但在存在运动物体或跨度较大的情况下不能得到稳定结果，因此本文在光流匹配得到特征点后，使用传统方法进行位姿求解。

光流估计网络选用经过训练的LiteFlowNet(Hui等，2018)，这是一个能够同时进行特征提取和光流计算的级联网络，且比传统方法能够在更大的感兴趣区域进行信息匹配。使用光流网络对连续图像进行稠密光流估计，由于网络估计出的结果不完全是正确的匹配，利用之前估计的前后向光流，在给定一定的误差允许范围内计算出前后光流一致部分(Zhan等，2020)，找到匹配度最高的一组点，如图3所示。

图3 光流匹配效果图Fig.3 Optical flow matching effect diagram

当获得2帧连续图像的匹配点后，将这组点送入RANSAC(random sample consensus)循环中不断寻找同分布的内部点(Fischler和Bolles，1981)，再使用8点法代入对极约束中求解本质矩阵E(Hartley，1997)，即

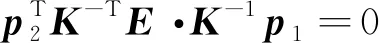
(8)

式中，p1和p2为同一3维点映射到对应两帧图像中的两个2维像素点，K为相机内参，t,R分别为对应位姿变换的平移与旋转矩阵。

应用奇异值分解(singular value decomposition，SVD)从本质矩阵分解相机的相对位姿[R,t](Kalman，1996)，求解结果有4种组合，其中空间3D点在两个相机坐标系中深度都为正值时为真正的结果。但其存在以下缺点：1)由于输入仅为两帧2维平面图像，不能获得位姿变换的偏移量t的具体尺度信息；2)当相机只进行旋转不进行偏移，本质矩阵为0，无法进行分解；3)如果相机运动过小(图像变化不明显)，会造成结果误差过大。因此，当对极约束不能求解时，即相机运动过小(平均光流<5个像素点)，使用PnP(perspective-n-point)，利用3D—2D关系进行位姿求解，其中3维坐标使用已经求得的相对深度图。在已知内参K的情况下，通过式(1)(2)根据最小化重投影误差求解出位姿。这种结果虽然不知道具体尺度，但得到的偏移量与相对深度的尺度相同，在进行尺度确定后还原出真实尺度的相机运动轨迹。

同样使用光流网络匹配有效点的方法还有以下两种方法，其中TBG(towards better generalization)方法(Zhao等,2020)为了解决长序列造成偏差累积过大的问题，没有使用位姿估计网络，而是利用光流网络匹配后的结果计算基础矩阵，并将深度估计与稀疏三角化的深度相对齐来监督深度和位姿网络。而EPC++(every pixel counts++)(Luo等,2020)同时运用深度、位姿、光流网络对图像中每个像素点的深度以及运动趋势进行估计，并且能够判断像素点是否为固定点或遮挡点，但其没有对深度图进行细致处理。

2.3 尺度恢复

本文主要应用于自动驾驶领域，并选择稳定识别且尺度不变的地面作为标志物进行初始尺度计算。为防止由于图像噪声引起的尺度偏差，额外引入车辆检测模块进行最终尺度补偿。

使用深度网络估计单帧图像的相对深度图，在获得相对深度值后，将每个像素点坐标[u,v,1]T按式(2)投影到3D空间内，3D坐标为[X,Y,Z]T。然后，依照8点法(Yang等，2017)，以每个像素周围的8个紧邻点进行表面法向量计算，这8个点分为4组，周围的8点每隔1个点为1组，使得每2个点与中间像素的向量垂直，因此这3个点构成的平面在3维空间依旧垂直，如图4所示。表面法向量计算为

(9)

(10)

式中，s表示不同的平面，范围在1 4，P1,s和P2,s为平面内除中心像素点(Ci,j)的另外两点。通过对两点到中心点的像素的向量求得叉积，得到垂直于平面的表面法向量ns。最后经过归一化和平均处理后得到中心点的表面法向量N(Pi,j)。

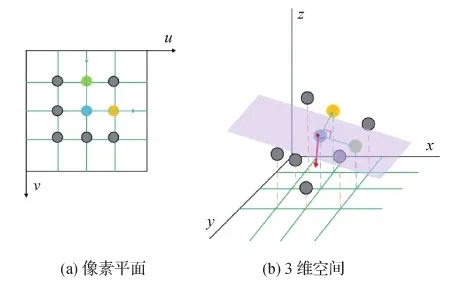
图4 8点法计算表面法向量Fig.4 Calculate the surface normal with eight-point method((a)pixel plane;(b)3D space)

图5 平面法向量计算地面点Fig.5 Calculate the ground points with the surface normal

该角度阈值为

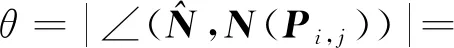
(11)

水平高度差H(Pi,j)由相机光心O到所有地面点Pi,j的向量OPi,j向对应点的表面法向量N(Pi,j)方向进行投影获得，也就是估计相机到地面的垂直高度。考虑到地面不是完全水平的，会由于图像中存在与车辆所处平面不同的地面即异平面而对实验结果造成误差。当异平面与车辆所在平面角度相差较多时，由异平面计算出的表面法向量会严重偏离垂直向量而被剔除出有效地面点。反之，当异平面与所在地平面角度接近时，在对所有有效地面点进行相机高度计算后，根据高度值分布情况选择概率最高的值作为最终相机高度估计值Hpred，从而排除周围环境带来的误差，且由于异平面角度相差不大，即使在出现异平面点占据多数的情况，使用后续的尺度补偿方法加权求和后也可以降低偏差对尺度的影响。具体为

(12)

式中，G表示地面点的集合。尺度计算引入相机先验高度H作为已知条件，用先验高度H与估计深度Hpred的商作为初始尺度。实验发现，在计算最终法向量时，由于深度网络估计的深度尺度会由光照突变、移动物体等因素造成部分不准确，仅依靠单个约束计算出的尺度具有不确定性，引入额外的车辆检测模块在能够检测到车辆信息时，应用小孔成像原理进行高度估计，并作为约束条件与初始尺度相互约束，降低初始尺度可能产生的偏差权重。即

(13)

式中，H为相机先验高度，h为图像中检测到的车辆高度所占像素点个数，f为相机的焦距，由于求得的结果是以像素点为单位，最终需要根据每个像素点所占实际物理距离进行转换，与初始尺度进行单位统一。最终尺度通过对初始尺度进行补偿得到，补偿方式由两个方法得到的尺度进行加权求和得到。具体为

(14)

式中，SGround和SCar分别表示地面点与车辆检测模块计算的尺度，参数λ1和λ2则表示两种尺度对应的分配权重，当SCar存在时，参数d为检测目标所在图像块平均相对深度，当SCar不存在时，直接取λ2为0，经过尺度恢复后的深度值如图6所示。

图6 补偿尺度的部分绝对深度Fig.6 Partial absolute depth with the compensation scale

3 实验结果与分析

实验环境为Intel(R)Xeon(R)E5-2620 2.10 GHz CPU，显卡为12 GB显存的TITAN X，系统为Ubuntu16.04。实验数据集选用KITTI(Karlsruhe Institute of Technology and Toyota Technological Institute at Chicago)2015数据集(Geiger等，2012)和KITTI odometry 数据集(Geiger等，2013)，前者用于深度估计网络训练，后者用于验证位姿准确性。数据集由4个彩色相机、1个64线3D激光雷达和1个GPS导航系统采集。

整个实验对深度估计结果和相机运动轨迹两方面进行测试。在深度估计方面，对本文方法与其他高精度算法在相同指标下进行评估，并对比不同功能模块对深度结果的影响。在相机运动轨迹方面，引入几何方法以及不同的网络估计方法的结果进行轨迹比较。

3.1 网络结构

本文的深度估计网络采用编码—解码形式的U-Net结构作为主干网络。为进行快速读取数据，首先将源图像格式由png格式转换为内存占用更小的jpg格式，并将原图截取至832×256像素大小后利用编码器网络提取特征，在获得特征图后利用Dispnet作为解码器将特征转换为逆深度图(视差图)，利用U-Net网络的跳跃连接结构将不同尺度的卷积结果与源图像和从低尺度特征上采样的结果相结合，避免了由上采样过程造成的局部信息丢失。深度值由视差图经过D=1/(d+b)转换而来，d表示视差，b一般为一个接近0的小数，防止分母为0，整个深度图约束在80 m范围内。

光流网络采用轻量准确的LiteFlowNet估计光流(Hui等，2018)，LiteFlowNet能够同时进行特征提取和光流处理，并且使用合成数据进行训练的结果，在真实数据上也得到了稠密、准确的结果。

检测网络整体基于ResNet结构，通过加入跳跃连接结构保存更多的局部信息，能够在多尺度下检测到目标。此外，为防止目标的重复检测添加了Softmax函数进行结果筛选。

3.2 效果评价

3.2.1 深度评价

本文在KITTI 2015数据集中采用Eigen分配方法测试，其中包含697幅测试图像，真实深度由3D点云数据利用内参投影后的2D深度图，测试时使用真实深度与估计值的比值进行还原后，再进行指标计算。评价标准为

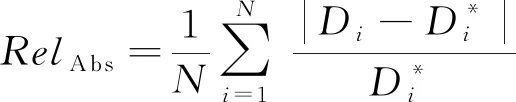
本文方法与其他优秀算法的对比结果如图7所示，详细误差数据如表1所示。

如图7所示，本文方法在轮廓和细节方面都明显优于其他对比算法，其中第1组告示牌下方的空白部分为天空，但大多数算法由于使用双线性差值且没有充分学习轮廓特征而无法显示细节部分，本文使用多尺度学习更好地保留了轮廓信息。第2组在出现多个原图难以辨别的路灯的情况下，深度估计仍然轮廓清晰，而深度结果接近的SC(scale consistent)算法，出现了深度不连续且运动车辆深度消失的现象。

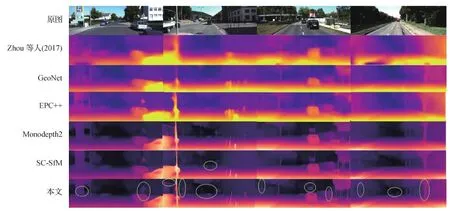
图7 不同方法的深度图对比结果Fig.7 Depth map comparison results of different methods

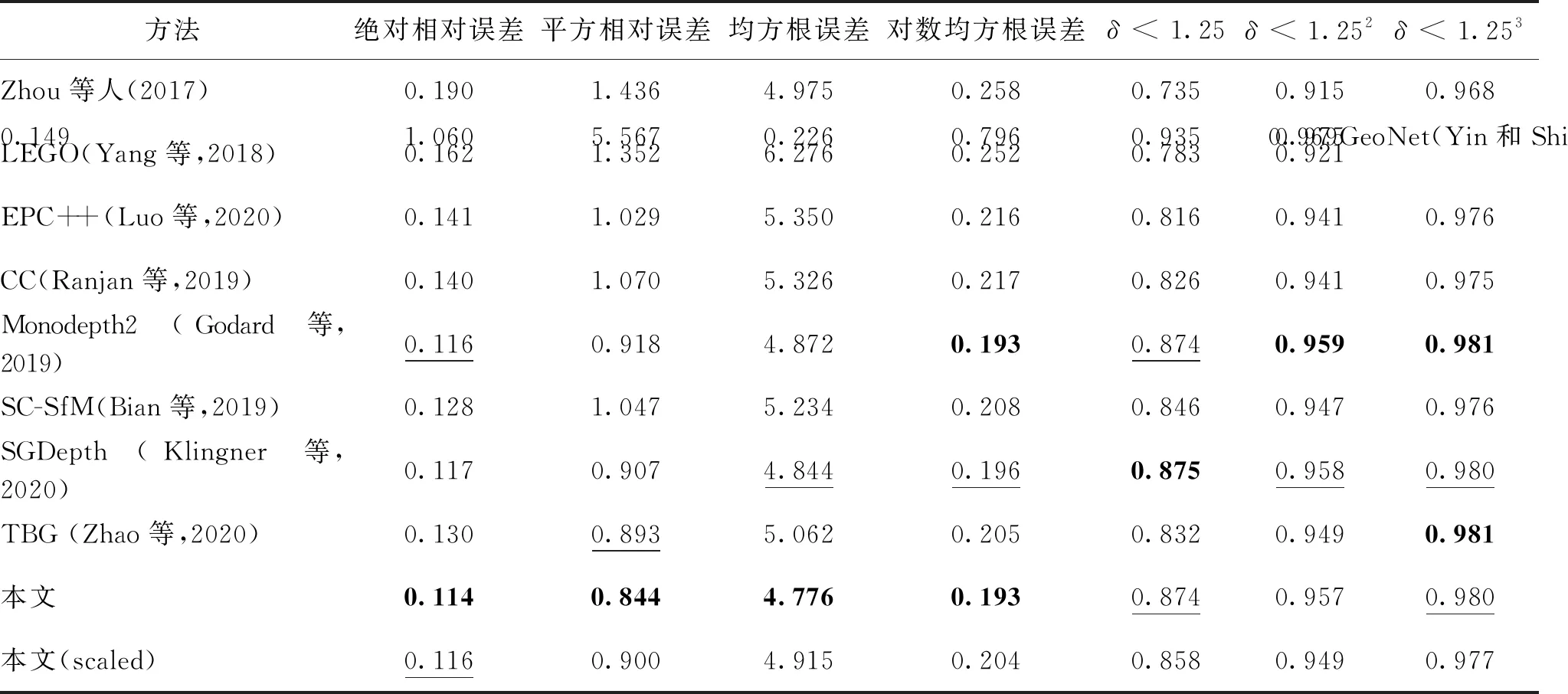
表1 深度估计算法误差比较Table 1 Error comparison among different depth estimation algorithms

3.2.2 轨迹评价

测试时引入基于深度学习的位姿估计(Bian等，2019)和基于几何的方法ORB(oriented FAST and rotated BRIEF)-SLAM(simultaneous localization and mapping)2(Mur-Artal等，2015)，对比结果如图8所示。

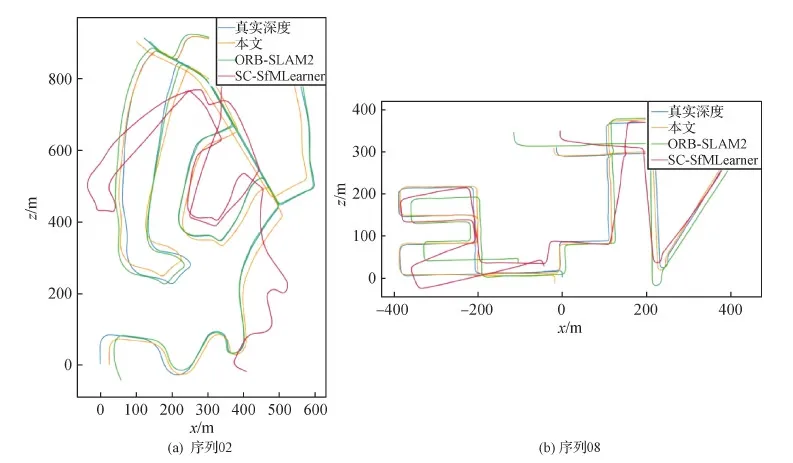
图8 相机运动轨迹对比结果Fig.8 Camera motion trajectory comparison results((a)sequence 02;(b)sequence 08)

对位姿结果的评价不是对所有位姿的误差计算，而是在子序列中估计为100 800 m距离处，每100 m进行一次位姿误差计算，误差包括平均偏移误差terr(%)和平均旋转误差rerr(°/100 m)。其中，绝对轨迹误差(absolute trajectory error，ATE) 测量真实值与估计值之间的[x,y,z]坐标的均方根误差。相对位姿误差(relative pose error，RPE)测量的是帧到帧图像间的相对位姿误差。

3.3 对比实验

为了证明尺度计算的有效性，对比两种不同的误差计算方式。1)直接利用真实深度均值(ground truth，GT)与深度网络估计的相对深度均值之间的比例进行整体放大；2)使用计算的最终尺度(scale)对相对深度进行尺度恢复。对比结果如表2所示。本文提出的尺度恢复结果在精度上不及使用GT值恢复的结果，但超过了其他对比方法的相对深度结果。更重要的是，在大部分样本中没有真实深度值进行监督条件时，本文方法在稍微降低精度的情况下，将没有实际作用的相对深度转变为含有尺度的真实深度值。

本文方法采用PyTorch 1.1框架进行训练，深度模型训练20周期，批处理大小为6个，平均训练时间8 h左右，而CC算法使用7天进行训练，SC算法使用32 h，Godard方法使用15 h。本文优化函数采用Adam优化器，学习率初始设置为10-4，并在后5个周期降为10-5进行细致学习，对单帧图像的深度图估计速度为0.2 s/幅。

表2 使用真实值与尺度计算的误差对比结果Table 2 Comparison result of the errors by using ground truth and scale

误差是估计结果与以单目序列作为数据集训练的其他算法模型的对比结果，相对误差结果均优于对比方法，整体准确度与Godard方法持平并领先其他方法，这是由于多尺度结构在增强局部细节信息的同时，会将不准确区域的误差累加，而使准确度略微降低。

本文使用尺度恢复的结果虽然在各项指标上不是最优结果，但与最优算法相差无几。更重要的是，其他算法均不含尺度信息，通过单帧图像生成的深度图仅能够表示相对信息，应用极其有限。本文使用两种不同约束条件相互约束以减小彼此间误差带来的影响，但纯视觉算法由于图像噪声等原因不可避免会产生偏差，且事实证明包含微小偏差对模型整体性能影响不大，且能够在保证高准确度的情况下得到真实尺度信息。

为证明损失函数的有效性，对不同的损失函数进行消融实验，结果如表3所示。其中Mask代表前后向光流一致度，S为经过补偿后的最终尺度。SSIM对于比较图像间的结构性关系特别有效，在光照变化明显情况下也能够稳定训练，而只依靠光度差和光流的方法则会严重依赖光照条件而影响学习效果。Mask将光流估计一致部分用做训练，使网络只学习有效信息，虽然不能很好地适应光度明显变化部分和透明区域，但能够有效解决遮挡和运动物体造成的影响，如图9所示，如果训练时没有考虑同向运动情况，连续图像中与车同速运动的自行车区域由于光度差过小，深度估计将此处更倾向于估计为无穷远处，从而产生黑洞现象。

表3 不同约束对深度误差的影响Table 3 The influence of different constraints on the errors of the depth estimation

图9 不同约束对深度结果的影响Fig.9 The influence of different constraints on depth estimation

检测模块利用空间关系计算补偿尺度SCar，在初始尺度SGround上进行加权加和的结果如表4所示，不难发现，准确度和误差是一个平衡的关系，当更多地重视检测模块时，检测部分区域的深度值因为受到监督而整体提升准确度。反之，依赖于地面点进行计算的结果在降低总体误差的同时，会导致估计深度逐渐偏离真实值，因此需要根据不同应用背景选择不同的侧重方向。

表4 不同补偿程度对深度结果的影响Table 4 Influence of different compensation levels on depth estimation

实验中，相机运动轨迹在序列05、07、08、09和10这5个较为复杂的路线中进行对比验证，结果如表5所示。可以看出，使用位姿网络估计的位姿结果在相对位姿估计的偏移量和角度误差上低于ORB-SLAM2，但由于缺乏尺度信息在绝对误差上有明显不足，本文方法使用经过光流筛选后的高匹配度特征点进行传统方法求解，并在求得的真实尺度后进行真实轨迹恢复，在相对误差和绝对误差上，都明显低于基于几何和网络估计的方法。

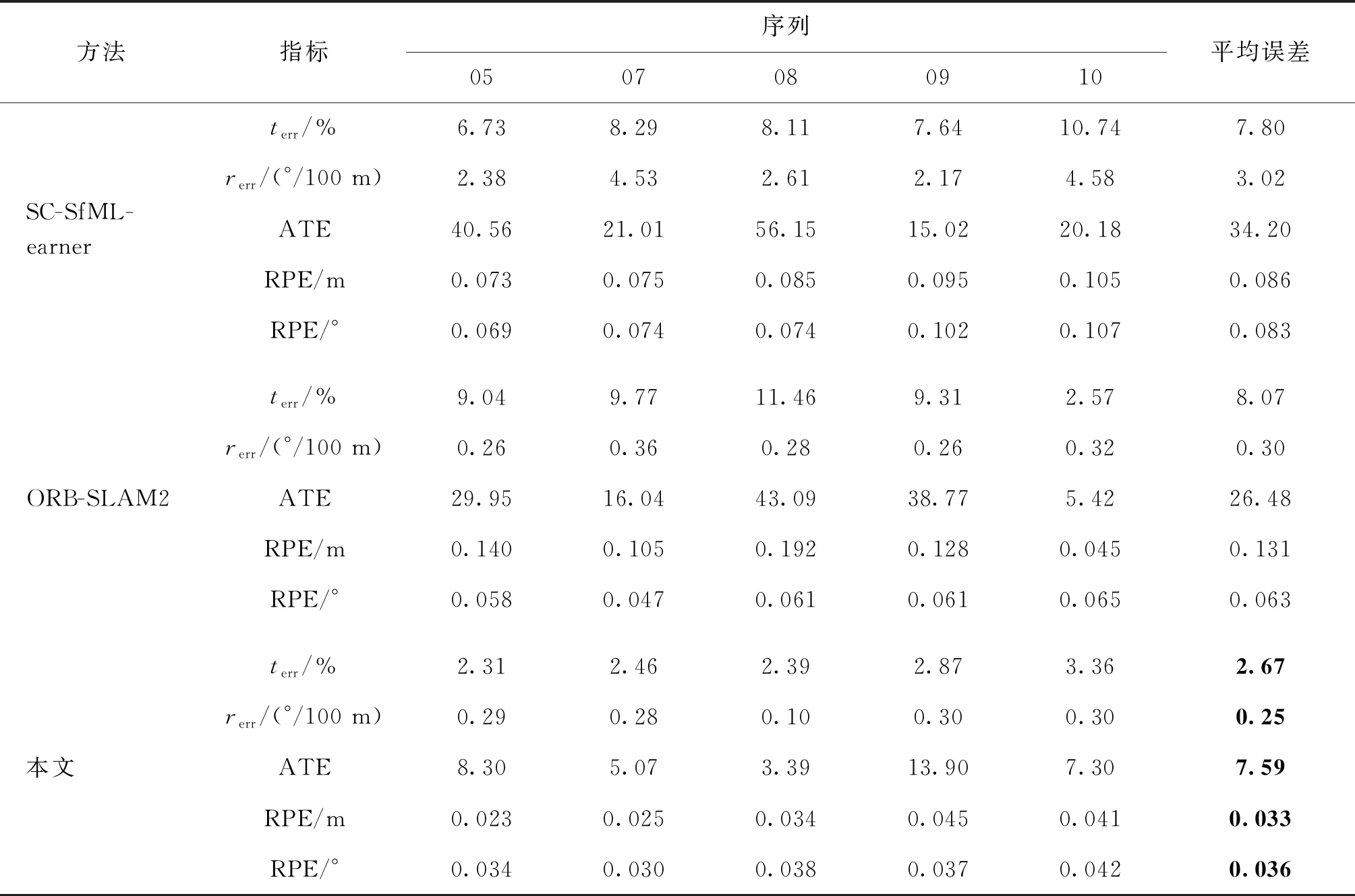
表5 基于几何和网络学习方法的相机轨迹误差结果Table 5 Camera trajectory error results based on geometry and learning-based methods

4 结 论

本文提出了一个利用场景几何关系进行真实尺度定位的单目系统，系统输入仅为单目视频序列且不需要真实深度标签作为监督，解决了单目视频序列生成轨迹容易造成的漂移现象，并计算真实尺度生成准确轨迹。经过尺度还原后的相对深度误差低于其他网络估计结果且包含尺度信息，计算出的相机运动轨迹与真实轨迹更加接近，在绝对误差和相对误差上都优于基于几何的ORB-SLAM和网络学习的方法，减小了由误匹配造成的漂移现象。然而，计算出的真实尺度仍有望进一步提高，这需要融入更多的先验条件对尺度进行补偿，即为检测模块的识别种类添加更多尺度不变的物体来增强约束。此外，为了能够将单目设备扩展使用至其他领域，在不能准确找到检测目标的情况下，最好的方法是引入融合惯导系统的单目设备，利用惯导生成的准确位置信息对生成轨迹进行校正，并有望在将来进一步将系统扩展至手机进行应用。