基于ANSYS普通圆柱蜗杆的模态分析

赵润发 黄娜 李琦 崔洪波

摘要： 本文主要研究普通蜗杆齿形和材料对其固有振动频率和模态振型的影响的大小。使用Creo8.0三维造型软件对蜗杆进行三维模型建立，然后利用ANSYS Workbench对蜗杆模型进行模态计算，得到蜗杆前10阶固有振型数据，并对数据进行对比分析得出结果。为蜗杆结构的设计与优化提供了理论依据。

Abstract： The influence of tooth shape and material on natural vibration frequency and modal shape of worm is studied in this paper. Creo8.0 3d modeling software was used to build the worm 3d model， and then ANSYS Workbench was used to calculate the worm model， and the first 10 order natural vibration mode data of the worm were obtained， and the data were compared and analyzed to get the results. It provides a theoretical basis for the design and optimization of worm structure.

关键词： 普通圆柱蜗杆;齿形;材料;模态分析

Key words： common cylindrical worm;tooth shape;material;modal analysis

中图分类号：TH122.5                                      文献标识码：A                                  文章编号：1674-957X（2022）05-0058-03

0  引言

蜗杆传动是一种通过空间相互交错的两个轴之间相互传递运动和动力的传动机构[1]。其对于传统齿轮传动来说，蜗杆传动比传统齿轮传动更具备工作平稳、冲击小、体积小、振动小、重量轻、噪声低、传动比大、结构紧凑、一些情况下具有自锁性等特点。被广泛应用于矿山、运输、国防、化工、冶金、起重等行业。

蜗杆副在工作时，会在外部激励和内部激励的作用下发生机械振动。所以在蜗杆的选取和设计过程中除了要对蜗杆副的基本参数进行设计外，还需对蜗杆副的固有振动频率和振型进行分析，避免发生共振现象，提高蜗杆副使用寿命，为蜗杆传动系统的动态设计提供参考。

唐熊武应用弹性力学有限元理论，采用有限元分析软件ANSYS对阿基米德蜗杆进行模态分析，得到蜗杆材料对固有振动频率和模态振型的影响。王敏利用HYPERMESH 软件对蜗杆进行模态分析。得到柔性体产生了弹性变形和振动，较好地模拟了蜗轮蜗杆传动动态接触变形特性，为齿轮箱蜗轮蜗杆系统动态设计提供了理论参考。

本论文主要通过利用Creo8.0三维建模软件对4种普通圆柱蜗杆即阿基米德蜗杆（ZA蜗杆）、渐开线蜗杆（ZI蜗杆）、法向直廓蜗杆（ZN蜗杆）和锥面包络蜗杆（ZK蜗杆）分别建模，研究其齿形和材料对其固有振动频率和模态振型的影响。分析对其影响的大小，并尝试通过改变一些小的因素改变其固有振动频率和模态振型避免在实际设计使用中与电机发生共振，加快破坏速度。

1  普通圆柱蜗杆有限元建模

本文使用Creo8.0三维造型软件对4类普通圆柱蜗杆进行实体建模。首先绘制草图，利用对称拉伸特征得到蜗杆主体毛胚模型，然后利用扫描移除工具绘制扫描曲线，输入螺距，绘制刀具齿廓进而进行扫描切除得到蜗杆主体实体模型，最后对蜗杆轴部进行实体生成得到如图1所示模型。

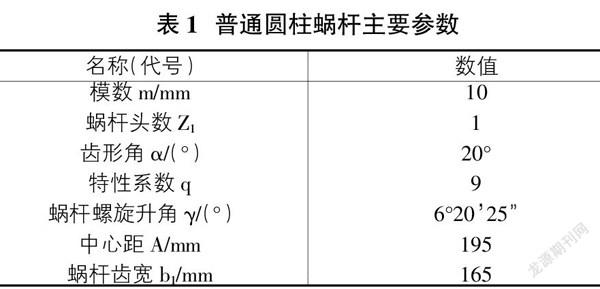
利用上述操作分别对阿基米德蜗杆（ZA蜗杆）、渐开线蜗杆（ZI蜗杆）、法向直廓蜗杆（ZN蜗杆）和锥面包络蜗杆（ZK蜗杆）进行实体建模。普通圆柱蜗杆的主要参数如表1所示。

2  蜗杆有限元分析

2.1 三维模型保存与导入

本文利用ANSYS Workbench 2020 R2對Creo8.0三维建模软件建好的三维模型进行模态仿真[2]。首先把建好的蜗杆三维模型保存*.x_t 格式文件，然后，导入ANSYS Workbench的 Geometry 中。

2.2 定义蜗杆材料与网格划分

本文主要研究的是蜗杆齿形和材料对其固有振动频率和模态振型的影响，分析对其影响的大小。其中为了研究不同材料对蜗杆固有频率的影响，本文使用了5种不同属性的材料对ZI蜗杆进行了模态分析，为了便于结果的比较，所有ZI蜗杆的尺寸大小不变，所选单元的类型、加载方式、求解方法均不改变，仅仅改变材料属性，ZI蜗杆所选的材料及其属性如表2所示。

2.3 网格划分

网格划分在有限元处理中占有重要的地位，是非常关键的一步。一个模型的结果好坏和正确与否，与网格的划分有着密不可分的关系。在有限元分析中模型的网格越密，得出的结果就越精确，同时对设备的存储空间和运算能力要求越高。本文使用自由网格划分方法，其中划分后的ZI蜗杆节点数为94137，单元数53652。如图2所示。

2.4 约束的加载

模态分析中，载荷、加速度、压力等会在模态提取时被忽略。但边界条件的约束施加非常重要。根据蜗杆传动的实际情况，需要在蜗杆两侧的阶梯轴端面安装接地的轴承支撑[3]。同时应该对蜗杆轴的切向运动设置自由转动。

2.5 模态分析理论

模态是机械结构的固有振动特性，其中模态分析又名自由振动分析，是探究结构动力特性的一种方法[4]，同时也是系统辨别方法在工程振动领域中的运用。模态分析的作用主要是确定有限元分析结构的固有频率与振型或者构件结构的固有频率和振型。同时模态分析也是谱分析、瞬态动力学分析和谐响应分析等的基础。每一阶模态都有其自己的固有模态振型、阻尼比和频率。一个拥有N个自由度的线性定长系统，需要将其离散成拥有若干个节点和若干个单多自由度系统，再结合振动力学以及有限元理论，得到其振动方程為[5]：

式中：[M]为系统总质量矩阵、[C]为系统阻尼矩阵、[K]为系统刚度矩阵;{}为振动加速度向量、{}为振动速度向量、{X}为位移向量;F（t）为节点动载荷。

一个系统一旦确定，那么这个系统的模态也就随之确定，也就是分析模态时不需要考虑系统的外部载荷条件，即{F（t）}=0，同时略去阻尼因素，得到无阻尼自由振动方程[6]：

3  模态分析结果

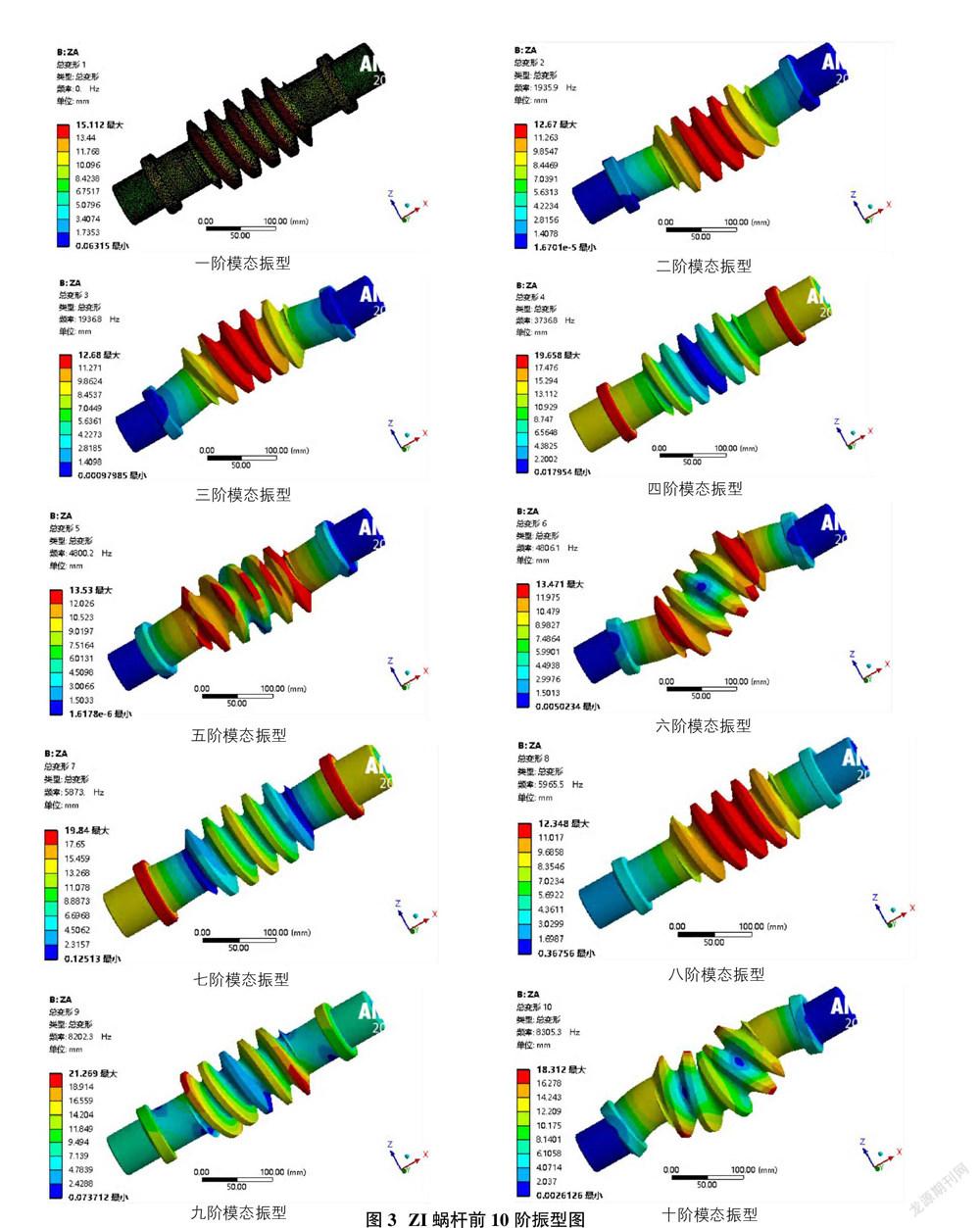
本文利用ANSYS Workbench对蜗杆模型进行模态计算。求出蜗杆的前10阶固有振动频率和模态振型。在模态分析中，阶数越低，影响也就越大，所以一般计算5～10阶的模态，精度就已经足够。其中渐开线蜗杆的前10阶各阶模态振型如图3所示。普通圆柱蜗杆的4种不同齿形前10阶固有频率如图4所示。不同材料的渐开线蜗杆前10阶固有频率如图5所示。

由图3可以看出，渐开线蜗杆前10阶各阶振型的情况，由于网格划分太过密集，为了便于图片更加快速有效的反映信息，所以一阶模型后去掉了网格显示。由图3可知此ZI蜗杆最大变形是在9阶处，此时的频率为8202Hz。其中变形量4阶和7阶次之。

从图4可以看出，蜗杆在其它条件不变的情况下，仅改变齿形前8阶固有频率曲线几乎是重合，9、10两阶固有频率也只是稍微的有点差别。其中前10阶固有频率曲线一直是锥面包络蜗杆固有频率曲线处于4种不同齿形蜗杆的固有频率曲线的最上侧，说明在其他条件相同时锥面包络蜗杆的固有频率是4种普通蜗杆固有频率最高的。而阿基米德蜗杆的固有频率曲线在前10阶中2一直处于4种普通蜗杆的固有频率曲线的最底端。至于渐开线蜗杆和法向直廓蜗杆则在前10阶的固有频率曲线相互交错多次。说明这两种齿形的蜗杆在其他条件相同时，固有频率几乎没有区别。

由图5可以得到不同属性的材料对ZI蜗杆固有频率的影响情况。本文选用了5种不同材料对ZI蜗杆进行了模态分析。由图4看出5种材料的ZI蜗杆的固有频率曲线几乎重合。其中20Cr与45Mn2的属性相近所以出现了图中材料为20Cr和45Mn2的ZI蜗杆固有频率曲线交错的情况。

而20Cr、45Mn2、12CrNi3和结构钢4种材料主要属性中密度几乎相同，只有泊松比和弹性模量不一样。从图中可以看出材料为结构钢的ZI蜗杆固有频率曲线在前10阶中始终低于其他3种材料的ZI蜗杆的固有频率曲线，而结构钢的泊松比比20Cr和45Mn2的大、比12CrNi3的小，只有结构钢的弹性模量是4种材料的最小值。从上面情况可以得出材料属性影响固有频率的主要因素是材料的弹性模量，且在其他条件相同情况下，材料的弹性模量越大其固有频率就越高。

材料为结构钢和1050的ZI蜗杆固有频率曲线也出现了交错的情况。但1050材料的弹性模量比结构钢低的多，其密度也低的多，所以由上述情况可以推断材料的密度也是影响材料固有频率的因素，且密度越低固有频率越大。

4  结论

使用Creo8.0软件建立了4种普通圆柱蜗杆模型，然后使用ANSYS Workbench对蜗杆模型进行模态计算。求出蜗杆的前10阶固有振动频率和模态振型。通过前10阶蜗杆模型模态结果的分析对比得出4种普通圆柱蜗杆在其他条件相同仅齿形不一样时，蜗杆的固有频率只有微小的变化。而其条件相同时，只改变蜗杆的材料得出弹性模量和材料的密度是影响蜗杆固有频率的主要因素。研究结果为蜗杆的结构设计优化和动态响应计算提供了一定的参考依据。

参考文献：

[1]濮良贵.机械设计[M].北京：高等教育出版社，1996：235- 238.

[2]卢利，牛鸣岐.基于ANSYSWORKBENCH的非对偶蜗轮蜗杆的有限元分析[J].现代制造，2011（12）：107-108.

[3]唐熊武，袁建畅，沈丹峰.基于ANSYS的阿基米德蜗杆模态分析[J].机械传动，2010，34（11）：62-65.

[4]崔勇俊，刘元.机械动态设计及模态分析[J].中国机械， 2014（6）：124.

[5]许本文，焦群英.机械振动与模态分析基础[M].机械工业出版社，1998.

[6]刘宜敞，等.蜗杆涡轮有预应力的模态分析[J].工业技术创新，2015，02（01）：3-7.