局部冷壁面多孔介质梯形腔内纳米流体自然对流
2022-02-26马兵善
王 磊,马兵善,王 刚
(兰州理工大学土木工程学院,甘肃 兰州 730050)
多孔介质梯形腔内的自然对流换热广泛存在于物料干燥、化学堆积反应床、热能储存、电子设备冷却和太阳能利用等工程应用领域中,研究其换热特性对我国的能源利用和节能具有很强的理论指导意义。而科研工作者面临的重要挑战是如何提高多孔介质梯形腔内的自然对流换热速率,满足日益增长的传热需求。Varol等[1]对多孔介质倾斜梯形腔体内的自然对流换热特性进行了数值研究,结果表明:总换热量随Ra数的增大而增大,随腔体倾斜角的减小而减小。Khan等[2]研究了多孔介质梯形腔体中自然对流换热,分析了Ra数、Da数、局部热壁面长度对温度场、流场、局部Nu数和平均Nu数的影响。
纳米流体作为一种新型高效的换热工质,能够显著增强换热效果[3-8]。Al-Weheibi等[9]根据Tiwari等[10]的数学模型,模拟了梯形腔体内的Cu-水和Co-水纳米流体的自然对流换热。在不同的Ra数、腔体宽高比、纳米粒子体积分数下,得到了流场、温度场和平均Nu数的结果。结果表明,纳米粒子在基液中体积分数的增加增强了传热速率。Esfe等[11]研究了碳纳米管-EG-水纳米流体在梯形腔体内的自然对流换热。在腔体顶壁冷却、底壁加热和左右侧壁绝热的条件下,讨论了Ra数、腔体宽高比、纳米粒子体积分数对流场、温度场和平均Nu数的影响。
综上所述,许多学者对梯形腔体中填充多孔介质自然对流换热和梯形腔体中以纳米流体为介质的自然对流换热进行了研究,而对以纳米流体为流动介质的多孔介质梯形腔体中自然对流换热的研究相对较少。此外,对于多孔介质梯形腔体中自然对流换热研究的重点主要集中在热壁面条件对自然对流换热的影响,而对局部冷壁面条件下梯形腔体内的自然对流换热的研究较少。因此,在局部热平衡假设的基础上,采用Brinkman扩展Darcy模型来描述多孔介质内纳米流体的流动,并在局部冷壁面条件下,对多孔介质梯形腔体内的Cu-水纳米流体自然对流换热进行数值研究,讨论Ra数、Da数、纳米粒子体积分数φ和局部冷壁面位置对流动换热特性的影响。
1 物理模型和控制方程
1.1 物理模型
所研究的物理模型如图1所示,填充均质、各向同性的饱和多孔介质(玻璃球为固体骨架)于二维梯形腔内,Cu-水纳米流体为腔体内的流体介质。梯形腔的上底长为H,下底长为L,高为L。梯形腔顶壁和底壁绝热,右侧垂直壁保持恒定高温Th,长度为S的左侧倾斜壁面上有一段长度为D且保持恒定低温Tc的冷壁面,剩余部分绝热。局部冷壁面采用3种布置方式:(1)局部冷壁面位于斜壁上部,与顶壁相邻;(2)局部冷壁面位于斜壁中部;(3)局部冷壁面位于斜壁下部,与底壁相邻。
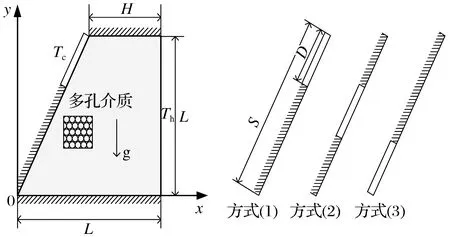
图1 物理模型Fig.1 Physical model
计算中用到的Cu纳米粒子、水和玻璃球的相关物性参数见表1。纳米流体热容(ρcp)nf、动力粘度μnf等物性参数的计算如表2所列[10]。表2各公式中下标f、p和nf分别表示水、纳米颗粒和纳米流体,φ为纳米粒子体积分数。

表1 水、玻璃球以及Cu纳米颗粒的热物性参数

表2 纳米流体热物性参数的计算公式
1.2 控制方程
在数值计算过程中,假设纳米流体为不可压缩、各向同性的牛顿流体;由Boussinesq假设来考虑自然对流效应。腔体中多孔介质固体骨架是均匀分布的玻璃球,满足无滑移边界条件,不考虑粘性耗散。二维多孔介质梯形腔体内Cu-水纳米流体的层流稳态自然对流的无量纲控制方程为
(1)
(2)
(3)
(4)
式(2)及式(3)中:ε为多孔介质孔隙率。上述方程中涉及的无量纲量定义为
(5)
其中:T0=(Th+Tc)/2,而αmnf为充满纳米流体的多孔介质的热扩散系数,计算公式为
(6)
其中:km为充满纯水的多孔介质的导热系数,计算公式为
km=εkf+(1-ε)ks,
(7)
其中:ks为固体骨架(玻璃球)的导热系数。
无量纲边界条件如下:
斜壁面低温部分:U=V=0,θ=-0.5;
斜壁面绝热部分:U=V=0,∂θ/∂n=0;n为倾斜壁面的法向量;
上、下绝热壁面:
(8)
右侧高温壁面:U=V=0,θ=0.5。
腔体高温壁面的平均Nu数计算公式为
(9)
腔体内Cu-水纳米流体的流动强度用无量纲流函数Ψ描述,其定义为
(10)
2 数值计算方法验证
压力与速度场的耦合问题由SIMPLEC算法求解[12]。对流项采用QUICK格式,考虑到存在高Ra数的自然对流,压力插值用PRESTO!格式。通过对文献[13]中多孔介质腔体内的自然对流换热进行数值模拟验证计算程序的可靠性,计算结果见表3。由表3可知,Nu数计算值和文献值的相对误差均在5%以下,这个误差是可以被接受的,证明该程序可以应用于后续的研究。对计算区域进行网格划分,为了获得网格无关解,采用了80×80、100×100、120×120、140×140四套网格进行了网格独立性验证。考虑计算的经济性,采用120×120网格进行计算。

表3 Nu计算值与文献[13]值的比较
3 计算结果与讨论
在数值计算中,梯形腔体倾斜局部冷壁面无量纲长度B=D/S=0.3、宽高比AR=H/L=0.5、多孔介质孔隙率ε=0.6、Pr=3.85,而纳米颗粒体积分数φ、Ra数和Da数的变化范围为:φ=0.02~0.1、Ra=103~107和Da=10-7~10-3。
在不同的腔体局部冷壁面位置时,Da=10-3、Ra=105、ε=0.6时腔体右侧高温壁面平均Nu数随φ的变化趋势如图2所示。由图2可知,平均Nu数随着φ的增加而增大,呈线性增长趋势。说明随着纳米粒子体积分数的增大,纳米流体的换热速率显著增强。随着纳米粒子体积分数的增大,纳米颗粒的随机运动增强,使得纳米颗粒和基液之间的相互作用增强,从而导致纳米流体内部热交换率和能量传递作用增强,因此强化了纳米流体的换热特性。同时发现,局部冷壁面按方式(1)布置时的平均Nu数最大,而方式(3)对应的平均Nu数最小。
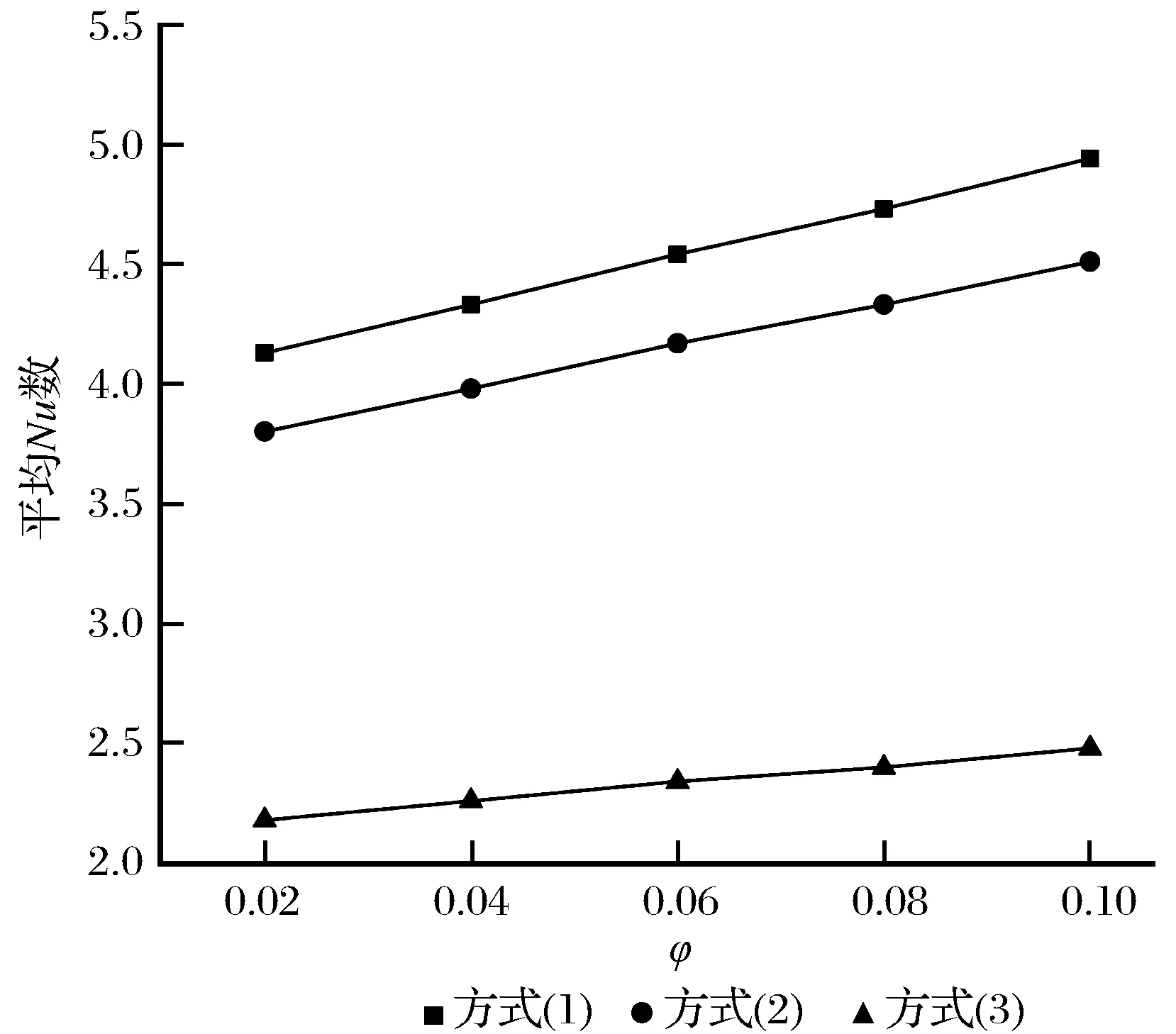
图2 不同的局部冷壁面位置时平均Nu数随φ的变化 Fig.2 Variation of Nu with φ at different positionof partially cooled wall
在不同的腔体局部冷壁面位置条件下,Da=10-3、ε=0.6、φ=0.04时右侧高温壁面平均Nu数随Ra数的变化趋势如图3所示。由图3可知,随着Ra数的增加,平均Nu数增大,呈单调指数上升增长趋势。说明Ra数对梯形腔体内纳米流体自然对流换热有较大的影响,且当Ra数较大时,梯形腔体内Cu-水纳米流体自然对流换热强度明显增加。因为当Ra数较小时,梯形腔体内浮升力相对较小,所以平均Nu数变化不大;当Ra数较大时,梯形腔体内的浮升力较大,梯形腔体内热量传递中对流换热的份额较大,自然对流换热效果进一步增强。从图3中还可以看出,局部冷壁面按方式(1)布置时的平均Nu数最大,而按方式(3)布置时对应的平均Nu数最小。

图3 不同的局部冷壁面位置时平均Nu数随Ra的变化 Fig.3 Variation of Nu with Ra at different positionof partially cooled wall
在不同的腔体局部冷壁面位置条件下,Ra=105、ε=0.6、φ=0.04时右侧高温壁面平均Nu数随Da数的变化趋势如图4所示。由图4可知,当Da数小于10-5时,平均Nu数的变化曲线呈接近水平趋势,说明Da数小于10-5时,梯形腔体内自然对流换热强度受Da数的影响较小。而当Da数大于10-5时,平均Nu数有了较为明显的变化,呈指数型增长。表明当Da数大于10-5时,受Da数的影响,梯形腔体内自然对流换热强度较大。Da数小于10-5时,多孔介质的可渗透度较小,粘性力较大,纳米流体的流动强度减弱,此时梯形腔体内对流换热较弱,热量的主要传递方式为导热。而随着Da数的逐渐增大,自然对流换热的强度基本保持不变。而Da数在10-4到10-3时,平均Nu数的变化几乎呈指数倍的增长,梯形腔体内呈现出旺盛的对流,表现为梯形腔体内纳米流体流动强度迅速增强。说明此时腔体内的换热形式由以导热为主转变为以对流为主,已经发生了根本性改变。从图4中还可以看出,局部冷壁面按方式(1)布置时的平均Nu数最大,而按方式(3)布置时对应的平均Nu数最小。
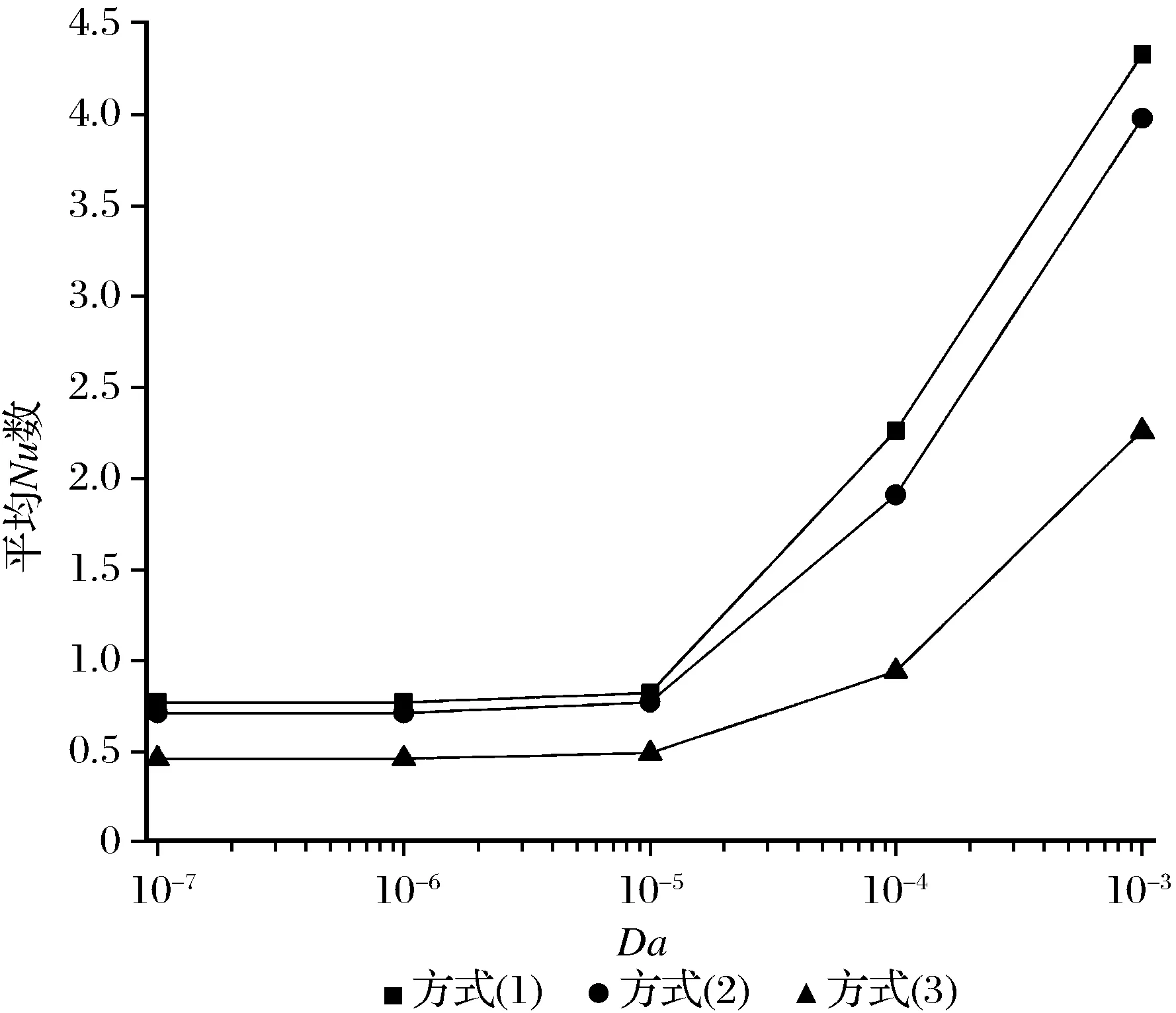
图4 不同的局部冷壁面位置时平均Nu数随Da的变化 Fig.4 Variation of Nu with Da at different positionof partially cooled wall
Ra=104、Da=10-3、ε=0.6、φ=0.04时不同局部冷壁面位置条件下多孔介质梯形腔体中Cu-水纳米流体自然对流换热的流场图和等温线图如图5所示。由图5可知,随着局部冷壁面位置向下移动,流场图中各流线所代表的数值逐渐减小,流体的流动强度越来越小;由于靠近热壁的Cu-水纳米流体被加热,受浮升力的影响,沿右侧壁面向上运动,而靠近冷壁的Cu-水纳米流体由于传热而向下运动,温度降低,从而在整个腔体中形成对流。当局部冷壁面位于腔体斜壁下部,与底壁相邻时,被冷却的流体运动到底壁的路程较短,运动到腔体底部具有更低的动能,从而导致流体流动强度减弱,对流换热强度减小。局部冷壁面位置对温度场也有一定的影响,随着局部冷壁面位置的下移,θ=0.45的温度线逐渐下移,说明随着局部冷壁面位置的下移,腔体上部逐渐被热流体占据,因此θ=0.45的温度线逐渐下移。因此局部冷壁面按方式(1)布置时的平均Nu数最大,而按方式(3)布置时对应的平均Nu数最小。
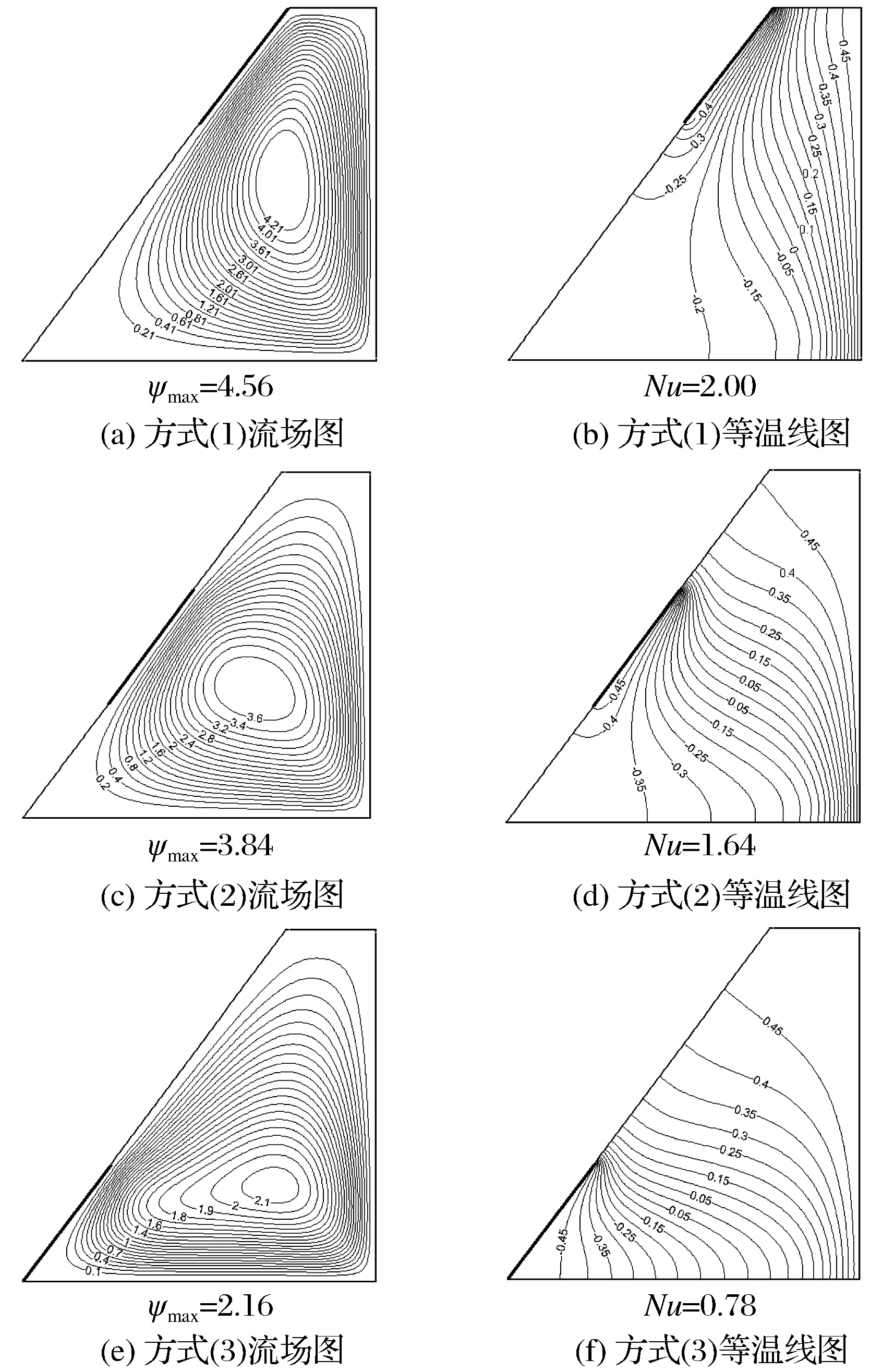
图5 局部冷壁面位置不同时流场图和等温线图Fig.5 Streamlines and isotherms at differentposition of partially cooled wall
4 结论
在局部冷壁面条件下,对Cu-水纳米流体在多孔介质梯形腔内的自然对流换热进行了数值研究,主要讨论了Da数、Ra数、纳米粒子体积分数φ和局部冷壁面位置对自然对流换热的影响。计算结果表明:在水中添加Cu纳米颗粒时可强化腔体内纳米流体自然对流换热,且随着φ的增大,平均Nu数增大;当φ和Da数一定时,随着Ra数增大,平均Nu数增大;当φ和Ra数一定时,随着Da数增大,平均Nu数增大。Ra数和Da数一定时,随着局部冷壁面位置逐渐向下移动,多孔介质梯形腔内Cu-水纳米流体最大流函数逐渐减小,对流换热强度减小。与其他2种局部冷壁面布置方式相比,局部冷壁面位于腔体斜壁上部,与顶壁相邻更有利于自然对流换热。
