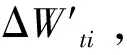煤岩弹性变形能的表征物理模型及实测方法

2022-02-26齐庆新李海涛郑伟钰杜伟升杨冠宇李晓鹏

煤炭科学技术 2022年1期

齐庆新,李海涛, 郑伟钰, 杜伟升, 杨冠宇, 李晓鹏

(1.煤炭科学研究总院深部开采与冲击地压防治研究院, 北京 100013; 2.煤炭科学研究总院煤炭资源高效开采与洁净利用国家重点实验室，北京 100013)

0 引言

煤的冲击倾向性描述的是煤体具有积聚变形能并产生冲击破坏的一种性质[1-4]，从具体力学行为的角度，该性质描述的是煤在受载条件下积聚弹性变形能的能力和失稳破坏时弹性能释放的剧烈程度。与之同样重要的概念是冲击危险性，即真实工程场景下发生冲击地压的危险性或可能性[5-7]。但根据已有的事故案例，煤体具有冲击倾向性并不意味着一定会发生冲击地压，而发生冲击地压的案例中，煤体也不一定具有冲击倾向性，二者高度相关但又互为不充分不必要条件。

煤岩介质的力学行为与应力环境密切相关，而冲击倾向性则是在国家标准要求的统一加载条件下获得的，其中，动态破坏时间(DT)和弹性能指数(WET)为应力加载，速度0.5～1.0 MPa/s，而冲击能量指数(KE)由于需要全应力-应变曲线，需要采取位移加载，速度为0.5×10-5～1.0×10-5mm/s[8]。这种测试方式能够为定性认知相近加载条件下，不同煤样冲击倾向性的相对强弱提供参考。但工程实际中的荷载变化区间更大、应力加载路径更多，而正是标准加载条件与实际加载条件的差异，造成了冲击倾向性测试结果与实际情况互为不充分不必要条件的现状。

狭义而言，标准测试条件下获得的结果才可被称为冲击倾向性，但若仅局限于此，造成上述不充分不必要关系的根源将只是冲击倾向性测试并未充分反映实际加载环境的多样性而已。冲击地压作为工程科学问题，对其研究的根本目的是为了在实际工况下降低或消除冲击危险性，简单地在概念或方法层面进行调整，而不深究其底层物理逻辑，显然满足不了有效防控的根本需求。

煤岩的特殊细观结构是造成其对于力学环境敏感的主要原因[9]，更具针对性地，细观结构与冲击倾向性的高度相关性也已得到验证，如煤的显微硬度、显微脆度、显微组分、原始损伤等细观特征与冲击倾向性呈正相关[10]；不同冲击倾向性煤样的细观结构在空间特征上存在显著差异；通过CT扫描获取单位面积裂隙周长、面积分数等统计性指标可实现对于冲击倾向性的定性评价等[11]。因此，对于冲击倾向性的底层物理逻辑，现有研究事实上已经给出了合理的关注方向。然而，煤岩具体力学行为是在应力、结构以及物性因素的共同作用下产生[12]，尤其对于细观结构的研究，目前还远未达到定量水平，由此带来的复杂度和制约性[13-14]使得尚未有成果能有效地将已获得的物理逻辑认知应用到具体的工程实践中去。

为此，笔者以挖掘冲击倾向性底层物理逻辑的工程指导路径为目标，通过分析现有冲击倾向性指标的设计特点，提出了在功能上能够反映弹性能积聚和释放的弹性损伤模型，并据此指出了冲击倾向性更为准确的物理内涵，依据简单可测的原则，给出了更接近真实情况的能量积聚和释放的监测手段、计算方法，为强化研究成果的工程指导能力做出了有益的探索。

1 现有冲击倾向性描述指标特点分析

冲击倾向性是对标准加载条件下煤样某种特定力学行为的概括描述，但为方便阐述其本质，同时避免新名词造成理解混乱，约定本文所述“冲击倾向性”不局限于标准加载条件。

冲击倾向性既然描述的是某种力学行为，依靠应力-应变曲线进行相关指标的设计是极为自然的，而现有指标也正是按照这一思路开展相关工作，并同时考虑了弹性能积聚和释放的描述。

目前，按照指标所关注的物理内涵不同，鞠文君等[15]将冲击倾向性指标划分为强度指标、时间指标、刚度指标、变形指标和能量指标，并列出了具体指标的计算方法，部分指标见表1。

表1 冲击倾向性代表性描述指标

文献对于冲击倾向性指标的相关研究做了较为详细的统计，由表1可直观地看出，目前常用的冲击倾向性指标设计基本全部依赖于应力-应变曲线，而依据不同加载控制方式所获得的应力-应变曲线则具有不同的描述功能：应力控制加载，可获得动态破坏时间等峰后跌落特性；位移控制加载，用以获得全应力-应变曲线；与前2种方式配合的循环加卸载，用以获得峰前弹性应变等指标。冲击地压的本质是弹性应变能的积聚和释放，循环加卸载和位移控制由于能够更好地支撑应变能计算而较多单独或配合使用。

循环加卸载的优势在于能够通过卸载和回弹，获得弹性段某加载点对应的真实弹性能积聚和耗散，进而评价介质存储弹性能的能力，但卸载点需要预估以保证加载处于试件的弹性阶段，从而在操作层面具有一定难度，同时，计算时通常期望获得峰值点前全部的弹性能积聚与耗散情况，在实际操作不可能的前提下，多假设峰前加载点对应的弹性能与总应变能的比值为常量，用之乘以峰值点前总的应变能，而获得而峰值点处介质存储弹性能的估算值，见表1中剩余能量指数WR。

位移控制可获得全应力-应变曲线，进而提供较为丰富的峰前、峰后力学行为细节，但目前多默认峰前为应变能积聚，而峰后为能量耗散，如冲击能量指数，也有将循环加卸载与位移加载结合，提高峰前弹性能计算的准确性。但客观事实是，应变能的积聚和耗散是伴随整个加载过程的行为，简单将峰前作为积聚或峰后作为耗散进行处理，在提供定性参考方面可能没问题，但由此也会使得一些细节被忽略，进而造成类似于冲击倾向性评价结果与实际危险性不符的情况。

综上，现有冲击倾向性指标的设计基本上全部依赖于应力-应变曲线，而设计的基本原则是期望准确描述加载过程中弹性能积聚和耗散的情况，循环加卸载和全应力-应变曲线是实现上述目标的有效手段，而需要关注的是，目前多将峰前作为应变能积聚阶段、峰后作为应变能耗散阶段处理，该做法能够定性描述介质存储弹性能的能力，但由于与客观事实不符，存在造成一定误导的可能，因此，有必要从还原客观物理行为的角度，明确冲击倾向性的本质，进一步提高冲击倾向性鉴定结果的可靠性。

2 煤岩弹性能量化表征物理模型

应变能多通过应力-应变曲线的线下积分获得，直观上是对曲线形态的一种描述，而现有指标设计多离不开对于峰值点的关注，峰值点作为曲线的拐点，其前后升降的物理内涵，将是揭示冲击倾向性本质的切入点。

首先，需要明确每个加载时刻前后所发生的力学行为，为此，需要构建能够反映介质受载基本行为的物理模型。对于冲击倾向性鉴定，多采用单轴加载，为描述方便，将模型的设计背景限定为位移控制的单轴加载。从能量角度，试件受载过程是试验机对其做功的过程，试件将产生2种主要响应，即能量积聚和耗散，前者来自于试件中完整部分的持续变形，后者来自于裂隙的发育、结构面间的摩擦、细观结构的破断等，其中，以结构破断所释放的能量为主，因此，本物理模型的核心功能侧重于介质的变形和破断。

此外，煤岩结构极为复杂，目前还尚未找到具有较好兼容性的量化描述方法，笔者将其简化为沿圆心均匀分布的理想弹脆性杆件。综上，试件可表征为统计损伤物理模型，其结构如图1所示。

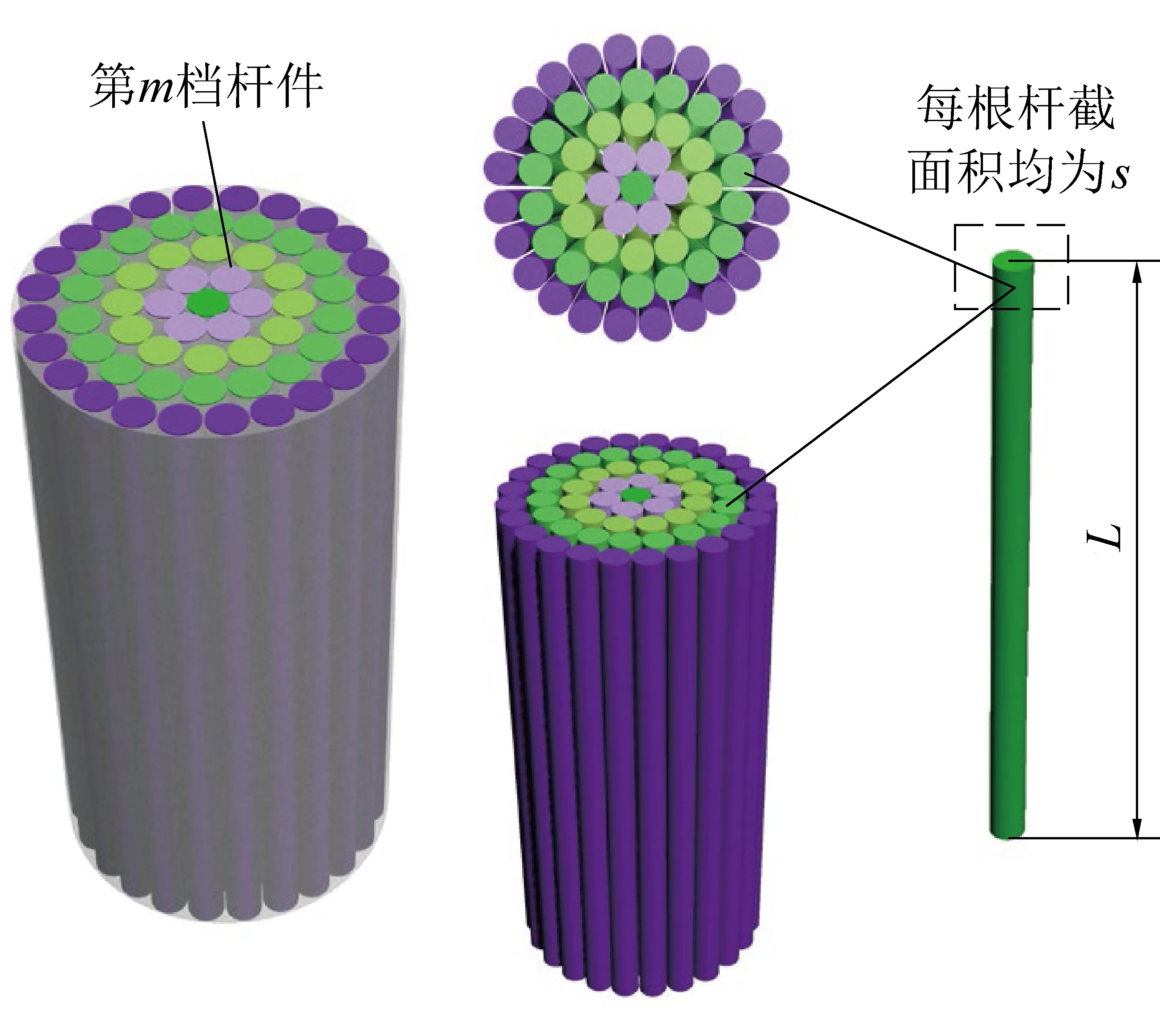
图1 统计损伤物理模型

其假设包括：

1)图中杆件共计N个，且所有杆件长度L和截面积s均相同。

2)按照承载极限最大值σmax和最小值σmin，依次将杆件均匀划分为M档，其中，第一档杆件承载极限σ1=σmin，第M档杆件承载极限σM=σmax，第j档(j∈[1，M])杆件数量为nj根，同档杆件围绕圆心均匀分布。

3)第j档杆件承载极限均为σj，弹性模量均为Ej，由此，每档的临界破断应变为εj=σj/Ej，并规定εa>εb(a,b∈[1，M]且a>b)，以此保证同档杆件同时破坏。

在明确模型基本假设后，将对模型施加位移控制的荷载，加载速率为u，加载时间按照时步计算，第i个时步记为ti。由此，若加载至ti时刻，1～(m-1)档杆件全部破坏，则该时刻试件所承受荷载为

(1)

类似地，ti+1时刻，随加载导致新增Δm档杆件破坏，则对应荷载

(2)

记Δt=ti+1-ti，则该时间段内荷载新增

ΔP=Pti+1-Pti=

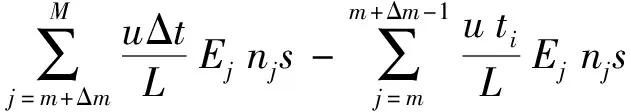
(3)

显然，对应于荷载位移曲线，若ΔP>0，则曲线表现为上升，反之下降，峰值点处该指标为0。新增荷载ΔP由2部分决定，首先是ti～ti+1时步内尚未破坏的第(m+Δm)～M档杆件产生单位时步应变，即uΔt/L，所需新增外部荷载的总和，需要注意的是，每根杆件产生单位时步应变所需的荷载uEsΔt/L为常量；其次是ti～ti+1时步内新增破坏的Δm档杆件，产生累积应变uti/L所需的荷载，由于符号为负，故可将其理解为反力。

若Δt为常量，则有

ti=iΔt

(4)

则式(3)简化为

(5)

进一步考虑能量特征，由于每根杆件的截面s和长度L相同，故每根杆件的体积V为

V=sL

(6)

则ti时刻试件产生uti变形，该时刻模型的变形势能Wti为

(7)

类似的，ti+1时刻模型的变形势能Wti+1为

(8)

则每时步模型能量状态的增量ΔWti+1为

(9)

令仍具承载能力结构新增变形能ΔW′ti+1为

(10)

令该时刻破断的承载结构所释放的变形能ΔW″ti+1为

(11)

则

(12)

从式中可以看出，每一时步内都会出现Δm档杆件破断，同时剩余杆件仍在承载的状况，而弹性能也是在部分杆件继续承载、部分杆件断裂的过程中逐渐累积，这与真实情况相符。

公式整体的物理意义可表述为：在考虑试件中承载结构变形和破断同时发生的前提下，令试件整体产生ΔtΔu位移时外载做所的功，等于该时步试件中仍具有承载能力结构中新增的变形能，与该时步破断承载结构所释放的变形能之差。由此，从理论上给出了外部荷载作用下，相邻时刻模型能量状态变化所对应的物理行为细节。

3 煤岩弹性能的实测方法

ti时刻模型变形能Wti，上述模型通过累加尚处于承载状态的杆件变形能获得，相关参量不可实测。但注意到

(13)

(14)

式中：εi为i时刻的杆件应变；σij为i时刻j档杆件单根应力。

将式(6)、式(13)、式(14)代入式(7)可得

(15)

而j档杆件所承受荷载Pij为

(16)

ti时刻杆件所产生的位移Si为

Si=Lεi

(17)

代入后可得

(18)

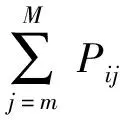
(19)

若不考虑承载结构空间形态的影响，即认为试件承载能力全部由结构的完整性来提供，则实测所得荷载Ps即可以用来表征P，由此，实现了Wti的可测，进而得到ΔWti的数值及演化曲线。

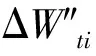
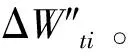
(18)

进而实现了模型由ti时刻向ti+1时刻变形过程中，完整介质中变形势能增量的实测，基于变形势能增量则可进一步计算累计变形势能。

随机选取具有复杂变化趋势的煤样，以验证上述方法的可操作性。该煤样在0.1 mm/min的位移加载条件下被压至破坏，其荷载-时间曲线如图2所示。

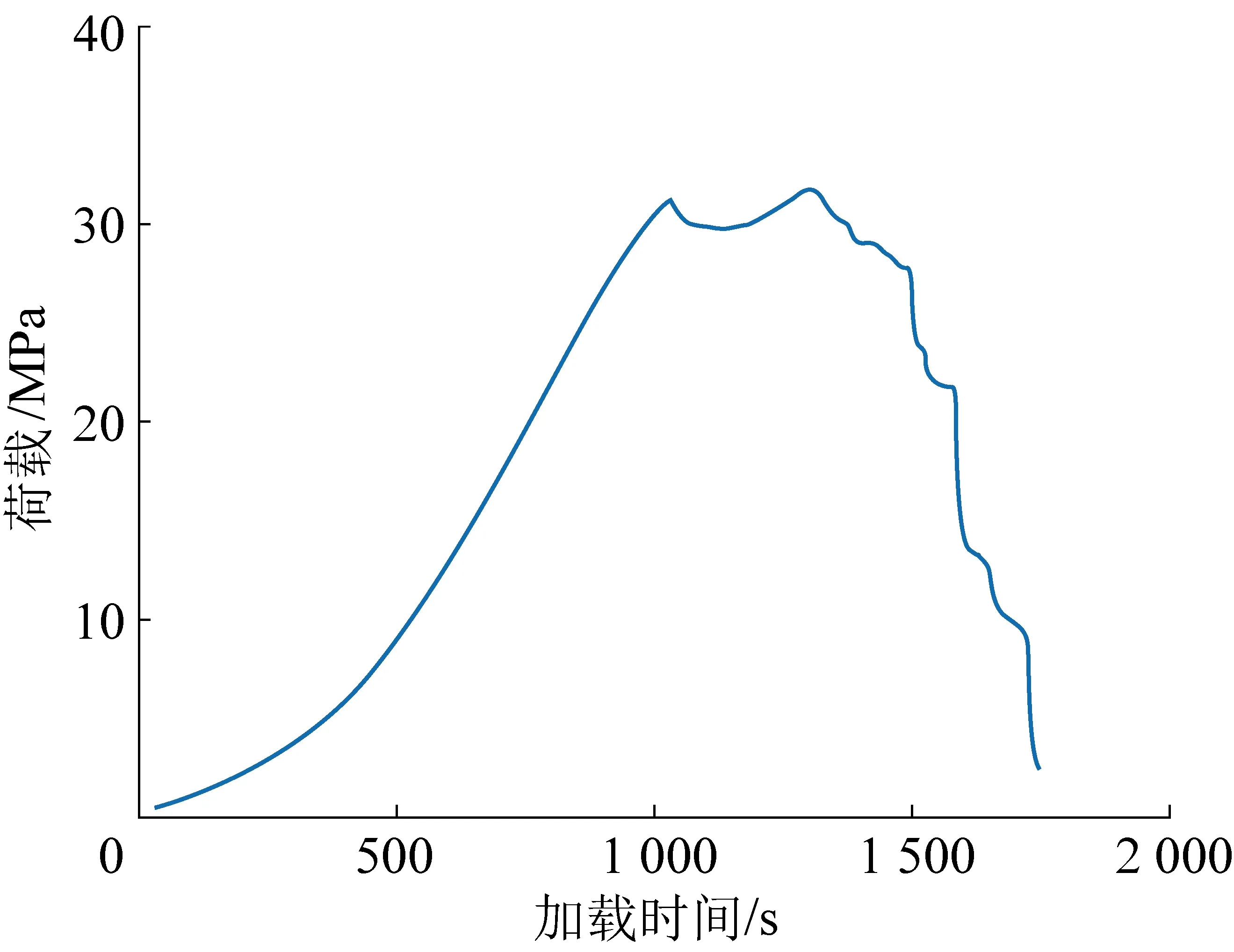
图2 验证试验荷载-时间曲线

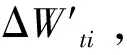
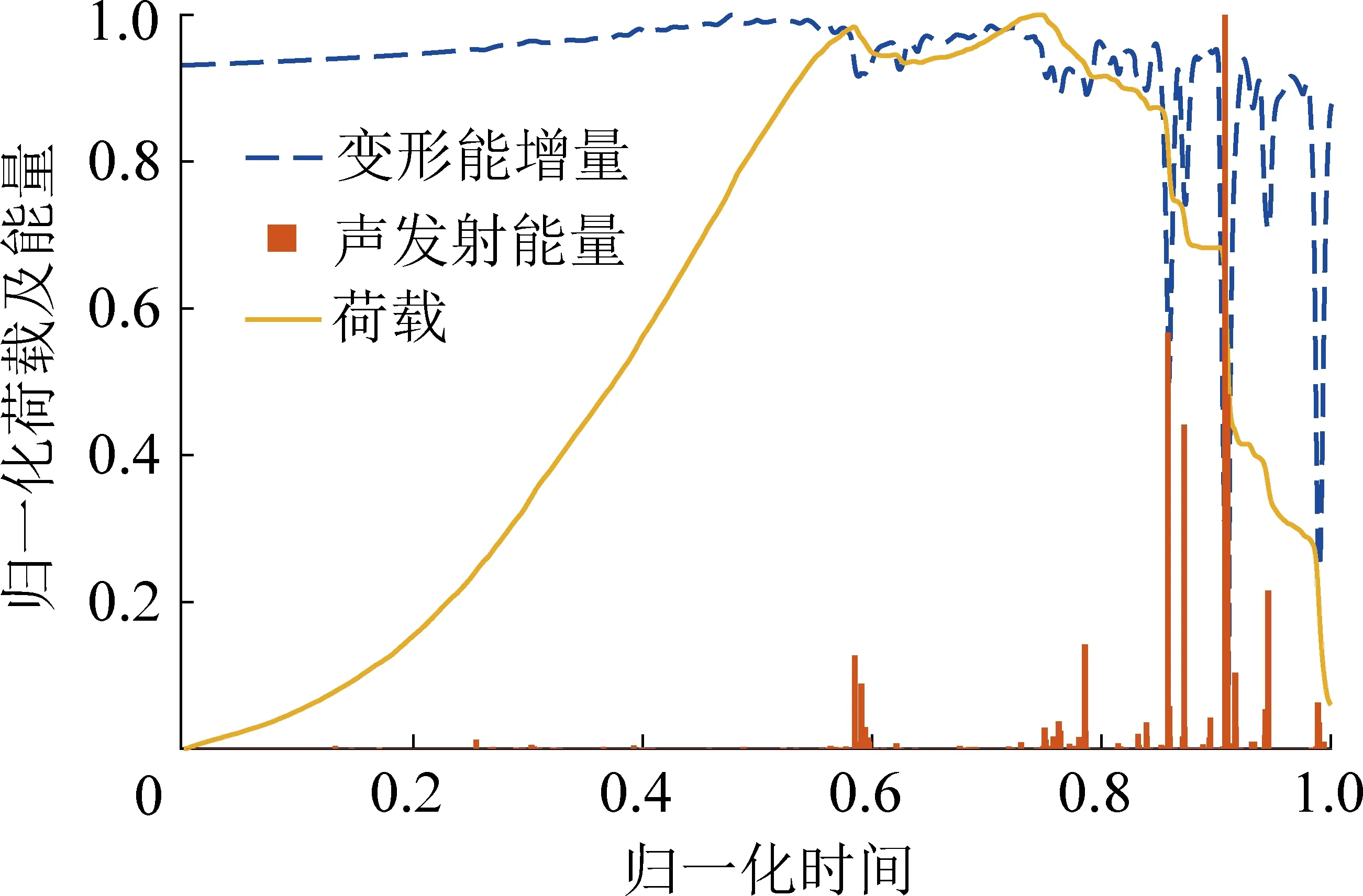
图3 变形能及声发射能量归一化结果

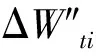
此外，依靠荷载-位移曲线获得的变形能增量，与依靠声发射测量的破裂事件能量，两种独立的测量手段在演化趋势上表现出了较强的对应性，从某种程度上暗示了该方法的潜在价值，但目前声发射监测设备所得的能量多利用门限电压上方的波形包络线计算，其单位是ms×mV(毫秒×毫伏)，并不能与加载所产生的变形势能(量纲为J，焦耳)直接进行融合计算，优化声发射事件能量计算方法，定制开发相关监测设备也是未来的攻关方向。

4 讨论

上述工作将试件受载情况下的物理逻辑反映到了变形能的计算当中，同时引入了声发射信息，在一定程度上逼近了弹性能真实值的实际测量，能够为后续的相关指标设计提供底层原理支撑。但煤岩本身的复杂性，使得该项工作也仅是在变形能测量模式上取得了有限进展。

目前的制约在于，无论是对于细观结构空间特征的描述还是针对其空间特征力学效应的试验，通常都采用了简化的手段以降低研究难度，而煤岩的复杂性体现在其随机多变的裂隙等结构要素上，上述简化操作恰恰忽略了这一关键因素，如裂隙发育对于结构强度的弱化作用，细观结构破断对于周边结构所产生的连带影响等，也正是由于此类的简化导致了室内测试结果对于工程实际参考性较弱的现状。

煤矿开采作为工程问题，通常存在对于准确性要求不高的惯性认知，但需要明确的是，危险状态的可靠判识是基于临界状态的准确描述，状态描述愈接近真实情况，所得结论的可靠性也将愈高，而随着工程条件下地面压裂、超长钻孔等大范围结构干预手段的成熟，将不再具备通过经验进行技术参数试错的空间，因此，煤岩细观结构甚至是冲击危险性的定量描述显然是具有现实意义的。