小波奇异熵改进 SOM 神经网络在道岔故障诊断中的应用

秦小虎

（重庆市轨道交通（集团）有限公司，重庆 401120）

传统的道岔故障根据微机监测系统采集的历史数据信息，由专家根据经验进行故障类型诊断，这种做法在实践过程中会出现人为误判[1]。为减少误判，文献 [2]将专家系统用在了转辙机故障诊断中，但是获取专家知识的过程相对困难；文献[3]将神经网络用于道岔故障诊断的方法需要采集大量样本；文献[4]用遗传算法优化支持向量机的方法原则上只能两两分类；文献[5]将贝叶斯网络引入S700K转辙机的故障诊断缺乏可靠合理的先验概率；文献[6]提出的基于状态参数的转辙机故障预测中参数变化模型难以建立。目前道岔类故障有机械类故障和电气类故障，实际诊断中发现机械类故障占大多数，为此本文选用6组机械故障和2组电气故障，使用小波奇异熵与Kohonen神经网络相结合的方法在故障时刻、故障位置、故障参数发生变化时依然能够识别故障，可以改善上述存在的大样本、模型难建立等问题。

1 小波奇异熵基本理论

1.1 Meyer小波分解

Meyer小波函数和尺度函数都是在频域中进行定义的，是具有紧支撑的正交小波。

式（1）中，a是构造Meyer小波的辅助函数，并且：

小波变换是一种新的变换分析方法，能够提供一个随频率改变的“时间-频率”窗口，能从时域和频域2 个方面反映信号的变化规律，因此小波变换的离散数学算法能用到道岔故障诊断中。

奇异值分解法公式如下：

式（3）中，X是m×m的矩阵；Y是m×n的矩阵；Z T是n×n的矩阵[7]。经过小波分解后的结果能用来表示原系数矩阵的基本特征，能得到：

其中对角线矩阵R的主对角元素ri（i= 1，2，…，l）为小波分解得到的奇异值，如果Dm×n能够反映时频特性，那么主对角元素就能反映基本模态特征[8]。

1.2 小波奇异熵的计算

小波奇异熵公式如下：

其中△Wi是第i阶增量小波奇异熵：

以测量的历史数据作为故障特征，依据小波变换、奇异值分解和泛化信息熵得到小波奇异熵，反映被分析信号的突变性，因为发生故障时小波奇异熵较大，所以故障诊断可以使用小波奇异熵[9]。

2 SOM 神经网络简介

自组织特征映射（Self-Organizing-Feature Map，SOM）神经网络也被称为Kohonen神经网络，它是一种全连接的自组织、无导师、自学习网络，根据不同的输入模式会产生不同的输出反映特性。

2.1 SOM 神经网络结构

SOM神经网络由输入层与竞争层2部分构成，如图1所示。输入层神经元有m个，竞争层是由a*b个神经元组成的二维平面阵列。输入层和竞争层之间实现了网络全连接的特性。

SOM神经网络的阵列一般最大是二维阵列，它们能够根据设计目的有选择性地提取输入向量模式特征，当阵列个数达到多维阵列时，网络模型会完整的包含处理单元的阵列、自我适应过程、比较和选择机制以及局部的互联作用。

2.2 SOM 神经网络的学习算法实现

SOM算法的特点是具备自我找到输入数据之间相似程度大小的能力，并由就近原则把相似的输入进行配置和分类，能够根据数据进行故障诊断，具体步骤如下。

（1）网络初始化设置。取输入权值m和输出权值两者之间的最小值。定义选择j和临近输出神经元组成集合Sj。其中，Sj(0)表示t= 0时临近神经元之间距离的集合，Sj(t)表示t时刻的临近神经元之间距离的集合。实验表明，Sj(t)随着时间的增长而减小。

（2）输入层输入向量。将选取合适的输入向量X=（x1，x2，x3，…，，xm）T添加到输入层中。

（3）统计出竞争层的权值向量与输入向量之间的长度（又被称为“欧式距离”）。竞争层第j个神经元与输入向量之间长度计算公式如下：

式（7）中，Wj是输出层神经元的权向量；xi(t)表示输入层输入值；ωij表示输入层的神经元和竞争层的神经元之间的权值。通过分析和实验可以得到最短长度的神经元（“胜出神经元”），将它记做P。

（4）权值的更新计算。更新胜出神经元P和邻接神经元间的权值：

式（8）中，ηt代表学习速率，其值位于0和1之间，最终慢慢降到0。

（5）输出Ok的计算：

式（9）中，f(*) 激活函数一般是0 ～1线性函数或者其他非线性类的函数。

2.3 SOM 神经网络的结论

通过研究算法本身和结果分析不难得出，网络的运行结果一般有2个明显特点：一是输出的拓扑映射结构是在各个兴奋状态下产生的一个完整结构；二是该网络映射结构具有自我组织的能力。

根据S700K转辙机的运行过程出现的故障原因分析和总结，可以得出常见的8种故障类型，其中包括 6 种机械故障（f1～ f6）和2种电气故障（f7、f8），故障分析如表1所示。

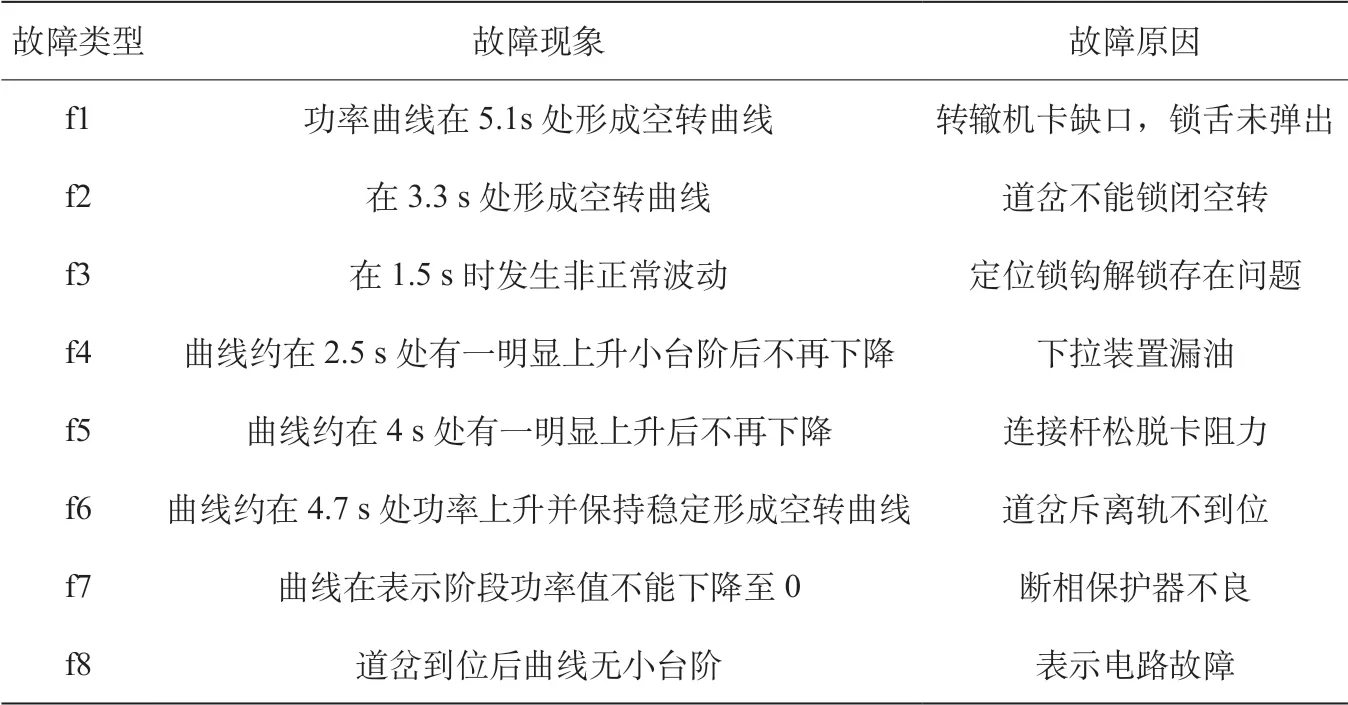
表1 S700K转辙机的典型故障分析

3 基于小波奇异熵和 SOM 神经网络道岔故障诊断模型的建立

基于小波奇异熵和SOM神经网络的道岔故障诊断流程如下（图2）：

（1）选择性的使用微机监测系统收集最近2个月内的200组数据，其中包含了S700K型转辙机工作状态的电流、电压、功率等表征量[10]；

（2）使用Meyer小波分解收集到的数据，得到40 组故障状态的数据信号，同时将剩余的数据信号用作Kohonen神经网络的训练数据；

（3）计算出第2步收集的40组故障类型数据的小波奇异熵，并将其做归一化处理，作为Kohonen神经网络的输入向量[11]；

（4）根据神经网络的输出数据，进行道岔的故障类型判断。

SOM神经网络在不同训练次数下的分类结果如表 2所示，当训练次数为10次时，可以将故障1、3分为一类，故障2、4、6分为一类，故障5、7、8单独为一类。可见，网络已经对样本进行了初步分类[12]。当训练次数达到200次时，每个故障都被划成单独的一类，此时的分类结果更加的精细。当训练次数达到500次或者1 000次时，同样也是划成为一类。可见，此时再去提高训练的次数，结果没有明显的变化[13]。

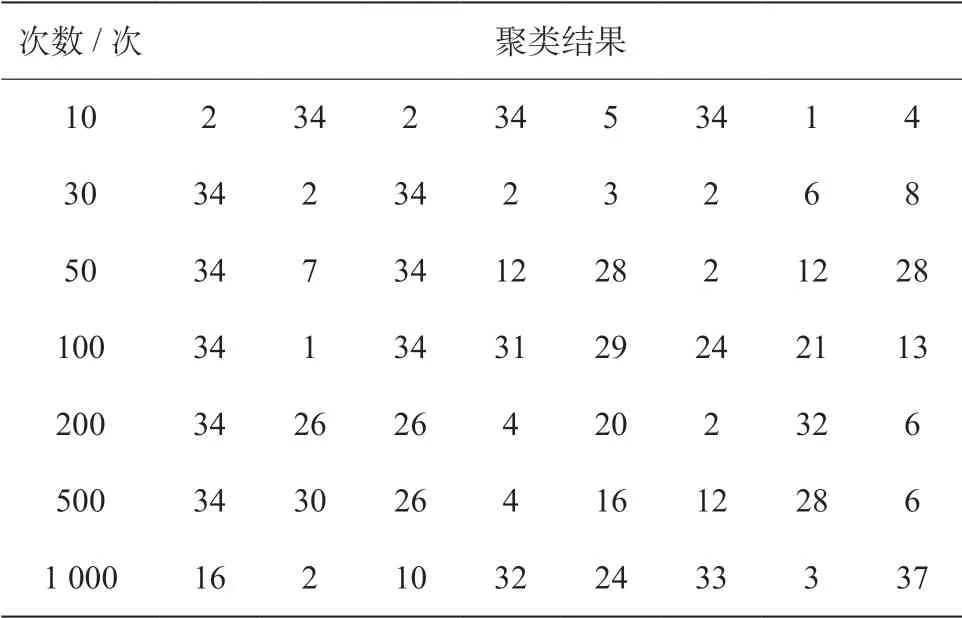
表2 SOM神经网络在不同训练次数下的分类结果

SOM神经网络的网络拓扑学结构如图3所示，竞争层的神经元总共有6×6 = 36个。临近神经元的直接距离如图4所示，其中蓝色表示神经元，红色表示直接连接的神经元，每个菱形的颜色代表神经元之间的距离的大小，黄色距离最小，越变成黑色，表示的距离越长。得到的每个神经元的分类情况如图5所示，蓝色神经元表示竞争胜出的神经元，神经元的输出为Y= [36，33，25，15，12，4，2，1]。经SOM神经网络训练后的权值矢量图如图6所示。

小波奇异熵改进的SOM神经网络与其他算法诊断结果对比如表3所示，由表可知，SOM神经网络相比FCM、K-means等聚类算法，拥有训练次数少、计算速度快、准确性高等优点[12]。

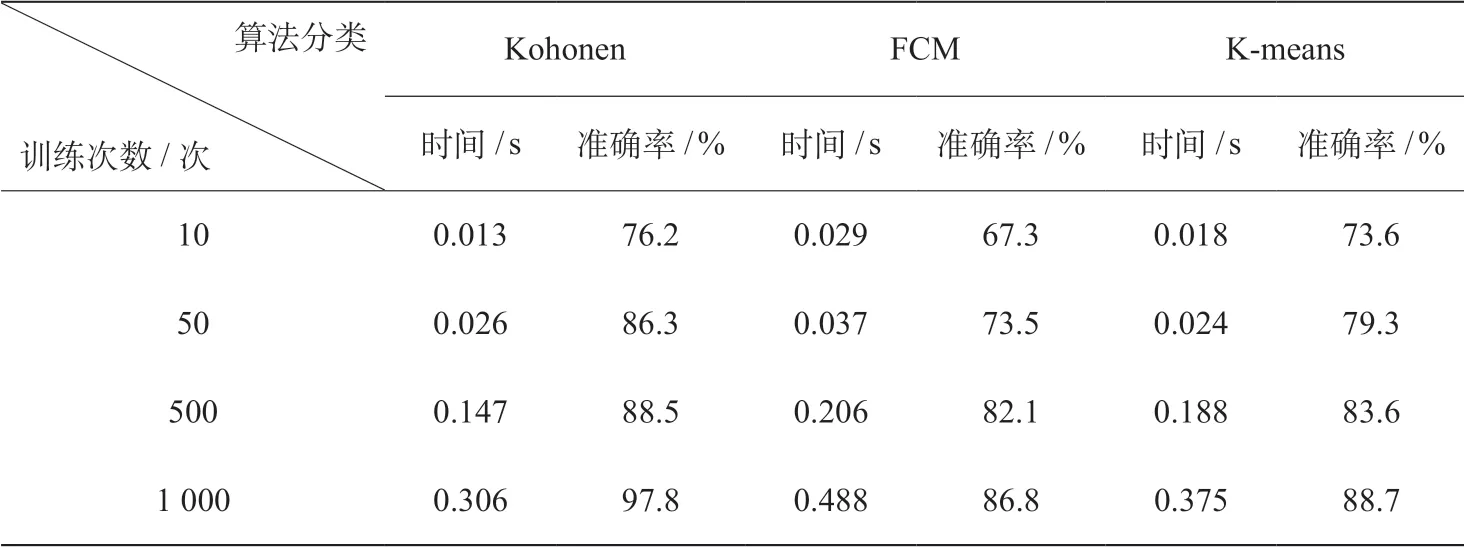
表3 小波奇异熵改进的SOM神经网络与其他算法诊断结果对比

4 结论

本文针对轨道交通道岔故障类型的多样性和表现数据的网络拓扑结构复杂性特点，提出了基于小波奇异熵改进的SOM神经网络的故障诊断方法。首先Meyer小波具有多重分辨率来刻画信号局部特征的特点，可以更好的分解数据，通过计算小波奇异熵作为网络的输入向量，再使用剩余的采集数据做为神经网络的训练集来建立诊断模型，仿真结果表明SOM神经网络准确度达到了97.8%，在仿真时间和训练次数上相比FCM和K-means等算法有着明显的优势，并且当道岔故障时刻、故障位置、故障参数发生变化时，仍能准确诊断。