基于最小二乘和BP神经网络算法的转辙机测力方法探究

(南京理工大学 自动化学院，江苏 南京 210094)

铁路运输向重载和高速方向不断的发展，对铁路系统的可靠性和安全性要求也不断提升。铁路道闸作为铁路网的咽喉和关节，是铁路网中较为薄弱的环节，也是事故频繁发生的地方[1]。转辙机作为道岔中主要的信号设备，对转辙机工况的监测十分重要。转辙机的牵引力能够准确地反映道岔转换是否到位[2]。目前国内转辙机测力的方法主要分两种：① 通过销式应变力传感器测量转辙机拉力，并在传感器内部嵌入微控制器、信号调理等电路。王安等[3]设计了单芯电缆传输的多转辙机拉力测试仪。该方法可同时测量多台转辙机牵引力，提高了测量效率，但传感器直接与转辙机相连接，会影响到转辙机自身工作的稳定性，只能起到临时测试的目的，不能达到实时监测的目的。② 通过采集转辙机的电气参数，计算转辙机的拉力。何迎春等[4]通过隔离采集转辙机电气参数，并基于功率不变、动能不变的原则换算为转辙机牵引力。该方法实现间接测量转辙机拉力，但需要对数据进行隔离采集，不能真实地反映转辙机实际工作下的牵引力。王安等[5-6]通过采集转辙机电气参数并将其转换为转辙机牵引力。该方法实现了实时测量转辙机牵引力，但电缆电阻和环境温度对测量结果影响较大。

最小二乘法作为一种优化技术，通过寻找最小误差的平方和来确定数据的最佳匹配函数。最小二乘法在土壤湿度传感器误差补偿[7]和连杆机构旋转轴定位精度补偿[8]等机械领域得到广泛应用。BP神经网络算法通过不断地进行信号的正向传播和反向调节，使得输出信号的误差达到一定的精度要求。刘影等[9]模拟退火算法改进四层BP神经网络后建立分类预测模型，提高了算法准确度。BP神经网络在测温湿度误差补偿[10]、测距误差补偿[11]、定位[12-13]以及避障[14]等机械领域得到广泛应用。

在前人研究基础上，为了填补转辙机牵引力在线测试的空白，提供一种非接触式实时测量转辙机牵引力的方法，利用激光位移传感器测量转辙机动作杆速度，并通过计算公式得出转辙机牵引力。考虑转辙机测力时既存在线性误差，又存在非线性误差，单一的补偿模型满足不了设备的精度要求，因此采用先通过最小二乘法补偿再通过BP神经网络补偿的双重误差补偿方法提高测量精度。

1 转辙机测力方法

1.1 方法简介

S700K在工作时电机旋转运动经过电机齿轮、小齿轮和大齿轮传递后经滚珠丝杠转换为直线运动，滚珠丝杠与动作杆锁闭连接由保持连接器完成，在保持连接器的作用下动作杆做直线运动。将直线运动系统折算为单轴拖动系统后，转辙机牵引力F与动作杆速度v成反比，与电机功率P成正比[6]。三级齿轮传动可等效为杠杆传动原理。因此，本方法通过激光位移传感器水平照射至转辙机动作杆尾端，通过数采卡将采集信号输送至上位机，测得动作杆“位移—时间”图像，并在上位机中换算为动作杆速度信息。将电机额定功率和动作杆速度信息带入测力公式并通过误差补偿测得转辙机牵引力。系统模型图如图1所示。

图1 系统模型图

1.2 建立转辙机测力模型

S700K转辙机的动力系统主要由电机、电机齿轮、中间齿轮、大齿轮、滚珠丝杠、保持连接器和动作杆组成，具体结构如图2所示。由齿轮传动原理可得三级齿轮组转速与齿轮半径成反比。大齿轮工作时与滚珠丝杠转速相同。转辙机动作杆通过保持连接器与滚珠丝杠连接，保证其速度与滚珠丝杠线速度相同，故动作杆速度等于滚珠丝杠螺距乘以滚珠丝杠转速。再结合“功率—扭矩”关系式、“扭矩—扭力”关系式及齿轮等效杠杆原理得牵引力测试公式如下：

n1∶n2∶n3=z3∶z2∶z1

(1)

v=n3·d

(2)

(3)

T=F1·r1

(4)

F∶F1=r3∶r1

(5)

式中：n1为电机齿轮转速；n3为第3级齿轮转速；z1为电机齿轮齿数；z3为大齿轮齿数；r1为电机轮半径 ；r3为大齿轮半径；v为动作杆线速度；d为滚珠丝杠螺距；P为电机功率；T为电机齿轮扭矩；F1为电机齿轮输出力；F为转辙机牵引力。

图2 S700K转辙机结构图

由式(1)～式(5)可得：

(6)

由于转辙机电机齿轮、中间齿轮和第3级齿轮的齿轮半径和齿数固定，故转辙机牵引力与动作杆件速度的倒数成线性关系，即需找到转辙机动作杆速度的倒数与转辙机拉力合适的对应关系。

2 转辙机牵引力误差分析

试验于转辙机试验台上进行，转辙机试验台通过手动调节压力挡位，使拉力在600～7000 N之间调节，通过激光位移传感器测得速度和拉力原始数据如表1所示。

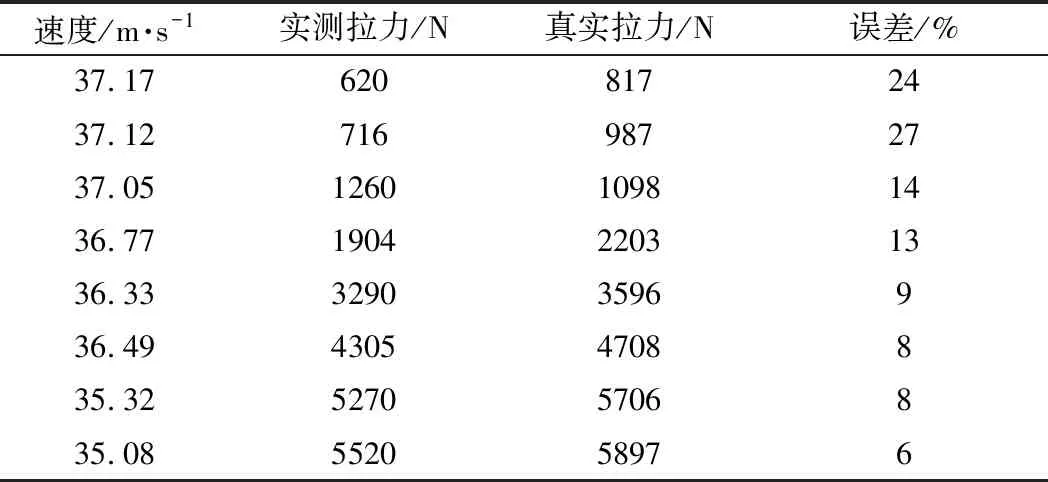
表1 转辙机拉力测量数据

由表1可以看出，拉力小时，转辙机的振动对测试结果影响较大，当拉力逐渐增加时，测试误差呈现减小的趋势。在转辙机测力系统中，转辙机测力误差主要来源于激光传感器安装误差、传感器自身误差和环境干扰误差。下面对误差产生原因进行分析。

① 传感器自身误差。由于激光传感器存一定倾角和表面粗糙度等，在实际测量中会对测量结果造成一定影响，降低测量精度。

② 激光传感器安装误差。激光位移传感器安装时需要保证激光水平照射至动作杆尾部，如果照射存在偏角，导致速度数据测量不准确。在安装激光位移传感器时可能存在安装时的机械误差，从而影响测量精度。

③ 环境干扰误差。外界测量环境如温度、湿度、以及转辙机震动等因素都会影响数据测量的精度。

综上考虑各方面误差影响，为提高转辙机拉力测量精度，采用软件算法补偿误差的方法：通过观测数据特征选取合适的算法补偿数据误差，以达到较高的测量精度。

由于转辙机本身振动和测试环境的干扰等因素，使得测试的误差较大，需要对测量数据进行误差补偿。

3 误差补偿方法

通过手动调节转辙机拉力，记录转辙机在不同拉力情况下动作杆速度的倒数与转辙机牵引力的关系，数据特征图如图3所示。根据数据特征图可知，动作杆速度倒数与转辙机拉力整体呈线性关系。在2000 N下，由于转辙机输出力较小，转辙机自身的震动对测量精度影响较大，所以呈现有规律的散点状分布。因此采用先通过最小二乘法初步补偿数据误差后再使用BP神经网络精细补偿数据误差的方法。

图3 数据特征图

3.1 最小二乘法改进算法模型建立

最小二乘法作为一种优化技术，是通过寻找最小误差的平方和来确定数据的最佳匹配函数。模型建立如下：

设经过m个数据点(xi,yi)(i=1,2,…,m)的线性拟合数据为

y=φ(x)=ax+b

(7)

任一散点(xi,yi)到直线y=φ(x)的最短距离为

(8)

(9)

为求得最佳线性拟合方程，需使ψ(a,b)取最小值即可。

3.2 BP神经网络算法模型建立

神经元作为神经网络的基本处理单元，一般可表示为一种多输入、单输出的非线性模型，其结构如图4所示，而方法中自变量仅为动作杆速度，故输入信号只有一个为动作杆速度。

其模型常用一阶微分方程来描述：

(10)

神经元的输出函数采用如下S型函数：

(11)

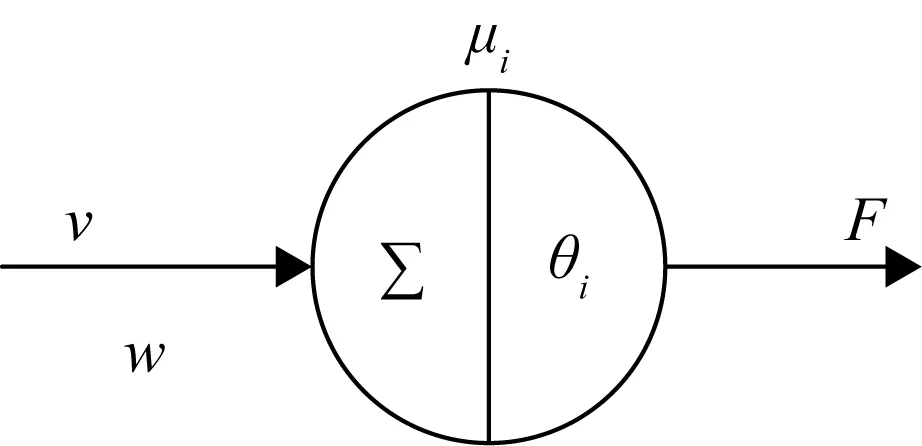
图4 转辙机测力神经元结构图

图4中：v为输入信号速度；w为权值；μi为神经元i中的内部状态；θi为阈值。

3.2.1 学习样本的处理

为了使预测数据更为精确，消除数据本身量纲对预测精度的影响，首先应对输入和输出的数据进行归一化处理，使数据化成[0,1]内的数值，其归一化的公式为

(12)

逆变化为

X=Xmin+Y(Xmax-Xmin)

(13)

式中：Y为归一化后的数据；Xmin为输入数据最小值；X为原始数据；Xmax为输入数据最大值。

3.2.2 隐层神经元数目的确定

根据经验公式：

(14)

式中：m为隐层节点数；n为输入层节点数；l为输出层节点数；a为取1～10之间的常数。

经过试验验证，当a取10时效果最好，隐层神经元数目为11。

4 实验验证

实验于南京电务段练功场内完成，通过手动调节转辙机拉力，试验条件如图5所示。在600～6000 N之间随机采集转辙机动作杆速度信息和真实的转辙机拉力信息在定位和反位运动中的数据，一组作为训练样本，一组作为验证样本。数据处理运用Matlab软件，最小二乘法使用polyfit函数对数据进行补偿，BP神经网络传递函数采用正切函数tansig，训练函数采用函数trainlm，权值阈值学习函数采用函数learngdm，性能函数选用函数mse，训练目标误差设定为10-3，最大训练次数设定为1000次。

所得转辙机拉力数据如表2所示，其中转辙机牵引力为转辙机手动调节转辙机测试台牵引力所得转辙机的实际拉力，计算值为测量后经过双重误差补偿的数据。

转辙机工作牵引力范围为1000～2000 N，1000 N以下数据环境对测量结果影响较大。故参考1000 N以上的测量数据并通过对比表1和表2数据分析可得，经过最小二乘法和BP神经网络双重误差补偿后，计算值与转辙机牵引力真实值基本保持一致，测量数据平均误差为7%。结果表明该方法满足转辙机牵引力测试要求。

图5 现场试验照片

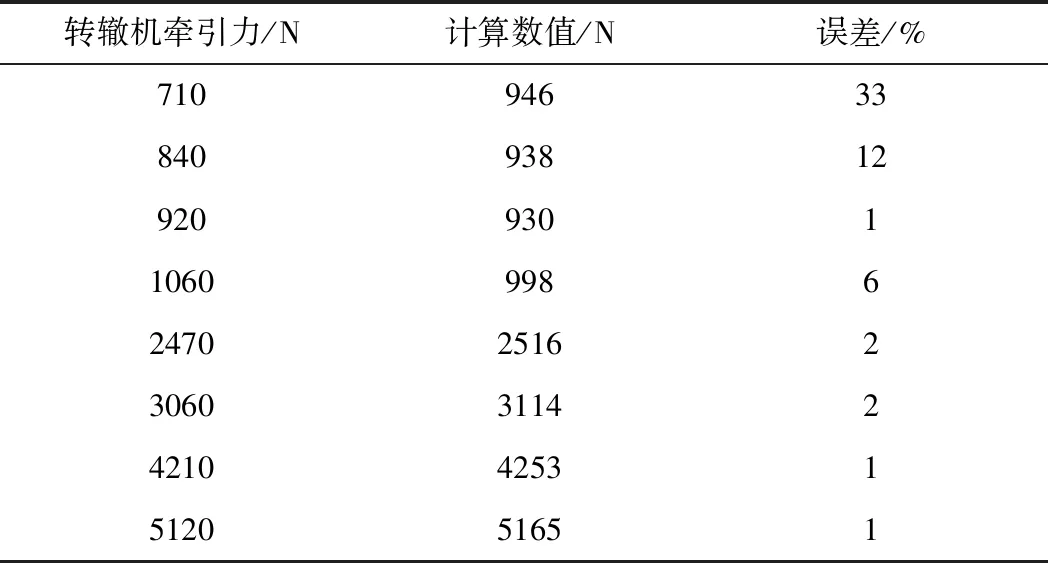
表2 转辙机拉力补偿数据

5 结束语

传统的转辙机非接触测力计是通过对转辙机功率信息或电机转速信息采集后换算为转辙机拉力，以上两种方法反映不了转辙机动作杆件的速度信息，且测量误差偏大。因此针对以上问题提供了一种非接触式检测转辙机牵引力的新方法。通过激光位移传感器获得转辙机动作杆速度信息，运用齿轮等效杆杆法建立转辙机测力数学模型，测量结果经过最小二乘和BP神经网络双重补偿得出转辙机牵引力。实验证明，该方法平均误差为6%，可以高效准确地测量转辙机牵引力。