Nearfield acoustic holography in a moving medium based on particle velocity input using nonsingular propagator

Bi-Chun Dong(董必春), Run-Mei Zhang(张润梅), Bin Yuan(袁彬), and Chuan-Yang Yu(俞传阳)

Department of Mechanical&Electrical Engineering School,Anhui Jianzhu University,Hefei 230601,China

Nearfield acoustic holography in a moving medium is a technique which is typically suitable for sound sources identification in a flow. In the process of sound field reconstruction, sound pressure is usually used as the input, but it may contain considerable background noise due to the interactions between microphones and flow moving at a high velocity. To avoid this problem,particle velocity is an alternative input,which can be obtained by using laser Doppler velocimetry in a non-intrusive way. However,there is a singular problem in the conventional propagator relating the particle velocity to the pressure,and it could lead to significant errors or even false results. In view of this,in this paper,nonsingular propagators are deduced to realize accurate reconstruction in both cases that the hologram is parallel to and perpendicular to the flow direction. The advantages of the proposed method are analyzed,and simulations are conducted to verify the validation. The results show that the method can overcome the singular problem effectively,and the reconstruction errors are at a low level for different flow velocities,frequencies,and signal-to-noise ratios.

Keywords: nearfield acoustic holography,moving medium,particle velocity,nonsingular propagator

1. Introduction

Nearfield acoustic holography (NAH)[1–4]is a powerful acoustic imaging technique firstly introduced by Williams and Maynard in 1980s. It allows sound source identification and sound field visualization by backward or forward projecting sound pressure or particle velocity measured over a surface in the nearfield of sources.

Usually,the NAH technique is applied to the sources located in a static medium. As for the sources located in a flow,such as wind tunnel applications,the conventional implementation of NAH cannot be applied directly because of the flow effects. In order to address this problem,Ruhalaet al.[5,6]proposed a new NAH procedure in a moving medium, including two cases that the hologram is parallel to and perpendicular to the flow direction. Due to the simplifying assumption that the particle velocity perpendicular to the flow direction is not influenced by the moving medium,the method is valid at low Mach numbers (M <0.2) but becomes inaccurate at higher Mach numbers, leading to significant reconstruction errors.In view of this, Kwonet al.[7]further proposed an improved NAH procedure without any simplifying assumptions,making it applicable to flows at arbitrary subsonic velocity. To realize accurate reconstruction with a relatively small hologram aperture, Kimet al.[8]proposed an improved statistically optimal NAH procedure in a moving medium,and Donget al.[9]developed a patch NAH in a moving medium based on sound field extrapolation. Considering the reconstruction of nonstationary sound field, Zhanget al.[10]proposed a NAH procedure in a moving medium using the time-domain equivalent source method, and Donget al.[11]developed a real-time NAH in a moving medium using derived convective impulse responses,including two cases that the hologram plane is parallel to and perpendicular to the flow direction.

In the above-mentioned NAH procedures in a moving medium, sound pressure measured by microphones is taken as the acoustic input. In fact, due to the interaction between the microphones and the flow, the measured signals contain additional noise. For low Mach numbers, the interaction is limited and the noise can be effectively removed by post-processing techniques.[7]However, for higher Mach numbers, the additional noise and disturbances of the flow pattern by an in-flow microphone array could yield significant reconstruction errors. To avoid this problem, Parisot-Dupuiset al.[12,13]proposed a non-intrusive planar NAH procedure in a moving medium with the particle velocity as the input, which can be measured by laser Doppler velocimetry.As pointed out by Parisot-Dupuiset al., due to the singular problem of the wavenumber-domain velocity-to-pressure propagator firstly derived by Kwonet al., real-space convective propagators are used instead to realize pressure reconstruction from particle velocity. Since there is no real-space velocity-to-pressure backward propagator, the reconstruction is realized by two steps, where the particle velocity on the hologram plane is firstly transformed to pressure by using the velocity-to-pressure propagator,and then the pressure is backward reconstructed by using the pressure-to-pressure propagator. In this procedure,the particle velocity gradient in the flow direction has also to be known by finite difference method,thus the measurement interval should be relatively small to ensure accuracy,and further it is difficult to realize reconstruction in the case that the hologram plane is perpendicular to the flow direction. In order to realize sound field reconstruction for sources with complicated geometry,Biet al.[14]proposed an equivalent source method-based NAH in a moving medium.By establishing an analytical relationship between the normal particle velocity on the hologram surface and the equivalent source strength, the NAH procedure can also use the particle velocity as the acoustic input. Due to the restriction that the hologram surface should be parallel to the flow direction,this method cannot realize reconstruction in the case that the hologram surface is perpendicular to the flow direction.

To realize an accurate non-intrusive NAH procedure applicable to both the cases that the hologram plane is parallel and perpendicular to the flow direction, a NAH procedure in a moving medium based on particle velocity input using nonsingular propagator is presented. By virtue of Laplace transform, new complex-frequency wavenumber-domain velocityto-pressure propagator without singular problem can be derived. With the new propagator, the reconstruction procedure can be implemented as the conventional NAH does, without any other information needed, such as the particle velocity gradient. Besides, two propagators corresponding to the parallel case and perpendicular case are obtained, and thus the proposed method can realize the reconstruction with the two cases accordingly.

This paper is organized as follows: The basic theory of the proposed method is described in Section 2.Numerical simulations are conducted to test the performance of the proposed method in Section 3. Finally, conclusions are summarized in Section 4.

2. Theory

In the Cartesian coordinate,the convective wave equation in a uniformly moving medium can be represented as[6]

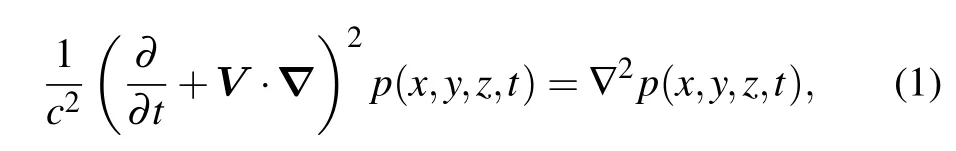
wherec,tandprepresent the sound velocity in a static medium, the emission time and the sound pressure, respectively,Vrepresents the velocity of a moving medium,∇2denotes the Laplace operator defined asand∇is defined ask,in whichi,jandkrepresent the unit vectors inx,yandzdirections,respectively.According to the relationship of relative position between the hologram plane and the flow direction,two cases that the hologram plane is parallel to and perpendicular to the flow direction are analyzed,respectively. In the following,the hologram plane is supposed to be in thex–yplane.

2.1. Parallel case

Assuming that the flow direction is in the positivexdirection,Eq.(1)can be represented as

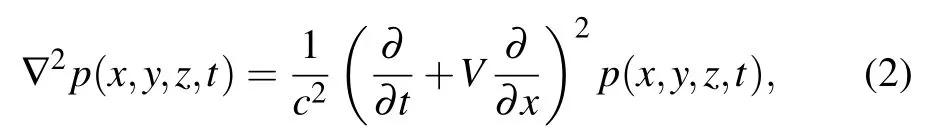
whereVis the amplitude ofV.

By using the Laplace transform

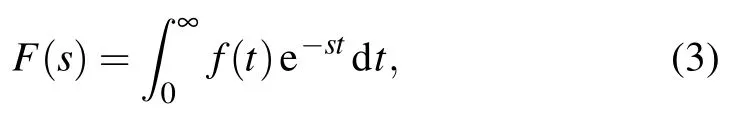
Eq.(2)can be expressed as

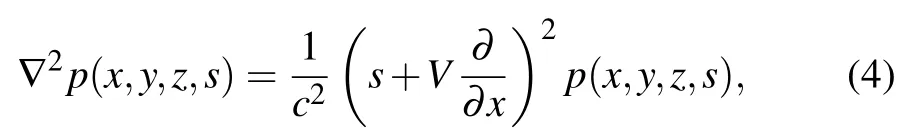
in whichs=σ+iωdenotes the variable in the complex frequency domain,σis the convergence factor andωis the angular frequency.

Then, by applying the three-dimensional Fourier transform

Eq.(4)can be rewritten as

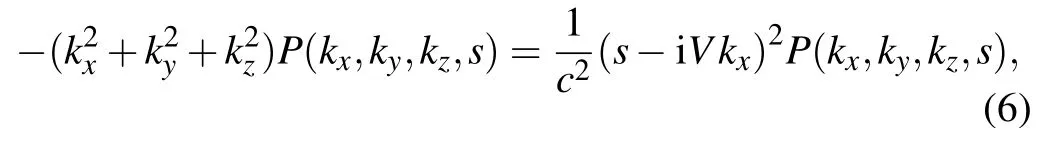
and this equation further yields

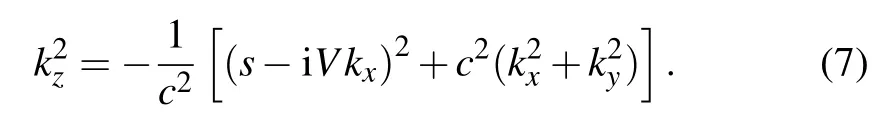
Substitutings=σ+iωinto Eq.(7),it can be obtained as

It is known that,kzdenoting the wavenumber component inzdirection is complex, and it can be generally represented as

wherekRandkIare constant,and denotes the real part and the imaginary part respectively. Consequently,it obtains

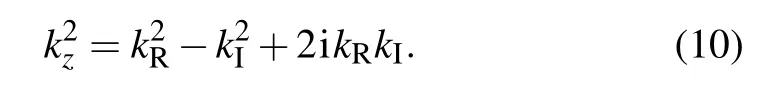
On the basis of the relationship that the real parts and the imaginary parts in Eqs. (8) and (10) should be equal correspondingly,it yields

From Eq. (11), the specific expressions ofkRandkIcan be deduced as

in which

By substituting Eq.(12)into Eq.(19),the specific expression ofkzcan be obtained.

Considering that the flow direction is in the positivexdirection and the hologram plane is in thex–yplane, the relationship between the pressure and the normal particle velocity on thex–yplane can be deduced from the convective Euler’s equation as[13]

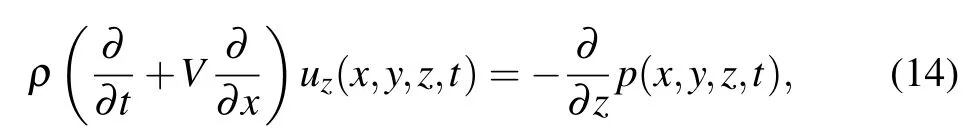
whereρis the density of the fluid medium,anduzrefers to the particle velocity inzdirection.

By applying the Laplace transform and two-dimensional spatial Fourier transform to Eq.(14),it yields

in whichkx,kyandkzrepresent the wavenumber components inx,yandzdirections, respectively, andPandUzare the spectra of the pressure and the particle velocity inzdirection in complex-frequency wavenumber domain,respectively.

Therefore,the spectra of the pressure and the normal particle velocity on thex–yplane can be related as

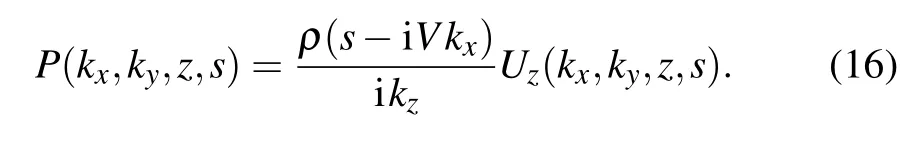
The relationship between the pressure spectrum on the reconstruction planez=zrand that on the hologram planez=zhcan be represented as

By combining Eqs.(16)and(17),the pressure spectrum on the reconstruction plane can be calculated from the particle velocity spectrum on the hologram plane,i.e.,

where

is the convective velocity-to-pressure propagator for the parallel case.

For comparison, the conventional convective velocityto-pressure propagator for the parallel case first derived by Kwonet al.is given as[7]

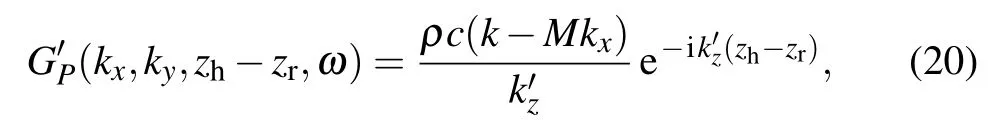
in which,k=ω/cis the wavenumber andM=V/cis the Mach number.

It can be observed from Eq. (20) that, there is a singularity on the radiation ellipse with, and this means aliasing will occur from sampling of the conventional propagator, resulting in reconstruction errors. As for the deduced velocity-to-pressure propagator shown as Eq. (19), the denominator ikzis a complex number that is easily proven to be always non-zero, and thus there is no singularity any more. That is to say, by using the Laplace transform in the time domain instead of Fourier transform as the conventional method does,the deduced propagator is presented in complexfrequency domain rather than frequency domain,and the singular problem can be avoided. The comparisons of the two propagators alongkx= 7.27 andky= 24.47 are shown in Fig. 1. Here, the Mach number is 0.3, the measurement intervals inxandydirections are 0.05 m, the propagating distance is 0.06 m, the sampling frequency is 12.8 kHz and the number of sampling points is 128. As for the convergence factorσ, although Wilcoxet al.[15]suggest an empirical choice that equals to the angular frequency interval Δω, it needs to be selected according to the actual condition,and in this paperσis selected to be 0.1Δω. From Fig. 1,it can be observed that the conventional velocity-to-pressure propagator presents singularity at some wavenumber components, while the deduced propagator in the proposed method is much smoother,which makes it easier to sample accurately in practice. In fact, the singular problem was also noticed for the velocity-to-pressure propagator in the static medium,and an integrated average form of the propagator was proposed to resolve the problem. However, there is no integrated form of the convective propagator,which is pointed out by Parisot-Dupuiset al. Thus, the proposed method provides another effective way to avoid the singular problem analytically.

Fig.1. The comparisons of the two propagators along kx=7.27(a)and ky=24.47(b).

2.2. Perpendicular case

Assume that the flow direction is in the positivezdirection,and Eq.(1)can be written as

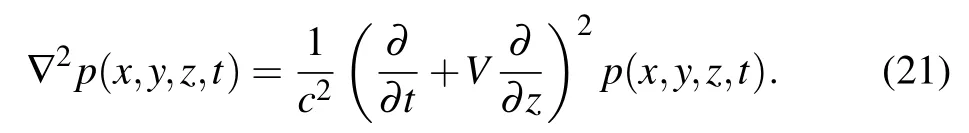
By using the Laplace transform with respect tot,it yields

Then, take the three-dimensional Fourier transform with respect tox,yandz,and Eq.(22)can be represented as

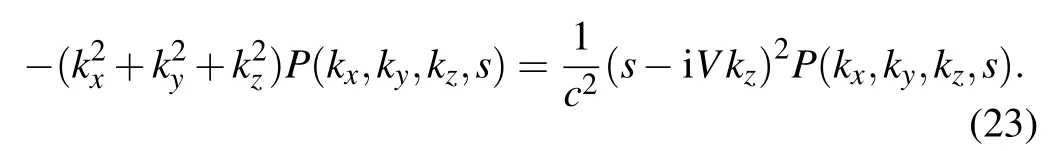
From Eq.(23),the wavenumber component inzdirection for perpendicular case can be obtained as

Substitution ofs=σ+iωinto Eq.(24)yields

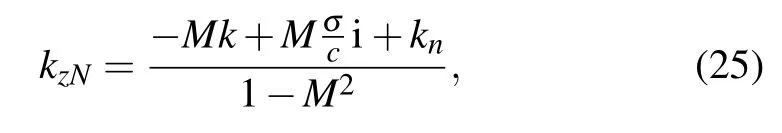
in which

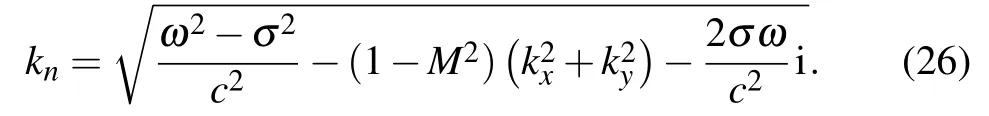
Due to the component in the root symbol is complex,it is necessary to determine the specific expression of the root square.

Considerknis complex,and it has the form

whereknRandknIare the real part and imaginary part ofkn,respectively. Therefore,the square ofkncan be represented as

Combining Eqs.(27)and(28)yields

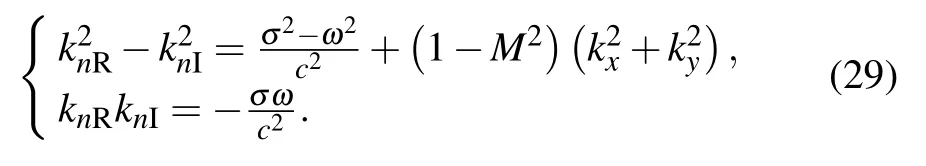
After some mathematical operations and combining the properties of sound wave propagation, the expressions ofknRandknIcan be obtained as

where

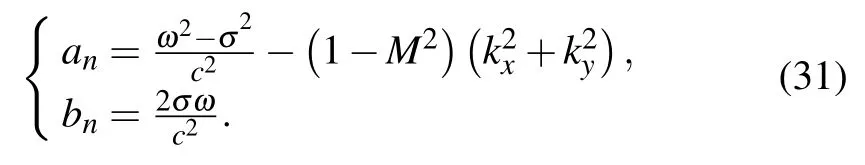
According to Eqs.(25),(27)and(30),the specific expression ofkzNcan be acquired consequently.

For the perpendicular case, the relationship between the pressure and the normal particle velocity on thex–yplane can be represented as

Apply the Laplace transform and two-dimensional spatial Fourier transform,and Eq.(32)can be rewritten as

By combining Eqs. (17)and(33), the pressure spectrum on the reconstruction plane and the normal particle velocity spectrum on the hologram plane can be related as

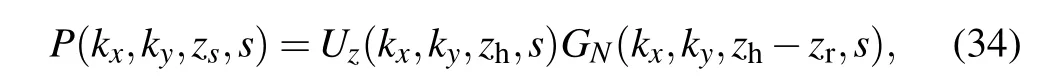
in which

is the convective velocity-to-pressure propagator for the perpendicular case.

To illustrate the advantage of the deduced propagator better,the conventional convective velocity-to-pressure propagator for the perpendicular case is given as[13]

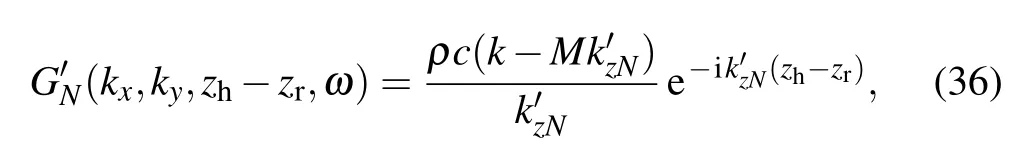
It can be observed that there is a singular problem forwhen,while the problem can be avoided for the deduced propagatorGN(kx,ky,zh−zr,s), due to the denominator ikzNis a non-zero complex number which is easy to be proven. The comparisons between the conventional convective velocity-to-pressure propagator and the deduced one are shown in Fig.2. Here,the simulation parameter settings are the same as those in the parallel case. The results show that the deduced propagator can effectively suppress the singularity at some wavenumber components corresponding to, and the magnitude of the deduced propagator at other wavenumber components are very close to those of the conventional propagator.

With the help of the above deduced propagators,the NAH procedure using the particle velocity as input without singularproblem can be realized, including both cases that the hologram plane is parallel to and perpendicular to the flow direction. The procedure is basically the same as the conventional NAH procedure. It is worthwhile to note that,to obtain the reconstructed pressure,the inverse Laplace transform and the inverse two-dimensional Fourier transform should be applied to the pressure spectrum. Furthermore,to restrain the noise components,the wavenumber-domain convective low-pass filter[7]is used in the reconstruction process.

Fig. 2. The comparisons of the two propagators along kx =15.21 (a) and ky=21.83(b).

3. Numerical simulations

In this section, numerical simulations are carried out to test the performance of the proposed method. The sound source consists of two monopoles located atS1=(0.1 m,0.1 m,0 m) andS2=(−0.1 m,−0.1 m,0 m). The hologram plane and the reconstruction plane are located atzh=0.06 m andzr=0 m,respectively. The dimension of the hologram plane is 0.55 m×0.55 m with 12×12 measurement points, corresponding to a measurement spacing of 0.05 m.By considering the parallel and perpendicular cases, the flow direction is assumed to be in the positivexdirection andzdirection, respectively. At first, the frequency of 1500Hz is analyzed, and the Mach number is set to beM=0.3, roughly corresponding to the velocity of high-speed train. To simulate the practical measurement conditions, Gaussian white noise with the signal-to-noise ratio(SNR)of 30 dB is firstly added to the measured particle velocity. The convective velocity potential atr=(x,y,z) radiated from each monopole source is given as

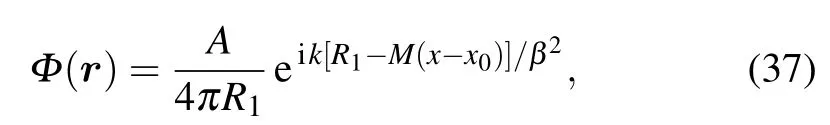
where,β=are the monopole source coordinates, and the constantAis set to beA=10−3. Based on the convective velocity potential,the particle velocity component inzdirection and pressure atr=(x,y,z)can be obtained as[13]

in whichuzrepresents the particle velocity component inzdirection,i.e.,in the direction normal to the hologram plane.The sampling frequency is set to be 12.8 kHz, and the number of sampling points is 128. To reduce the wraparound errors associated with the two-dimensional spatial Fourier transform,the particle velocity on the hologram plane is zero padded,and the size after zero-padding is eight times of the size of the hologram plane.

In order to illustrate the proposed method better,the conventional NAH procedure in a moving medium presented in Ref. [7] are also used to realize the reconstruction, and the comparisons between this method and the proposed method are performed. The reconstructed and theoretical pressures on the reconstruction planezrfor the parallel case are shown in Fig.3, while the results for the perpendicular case are shown in Fig. 4. From Fig. 3, it can be observed that although the two monopoles can be identified by the proposed method and the conventional method, the differences between the reconstructed results by the conventional method and the theoretical ones are apparently larger than those between the results by the proposed method and the theoretical ones. From Fig.4,it can be seen that the pressure reconstructed by the conventional method significantly deviates from the theoretical ones,while the pressures reconstructed by the proposed method are in good agreement with the theoretical ones.For quantitatively describing the reconstruction accuracy, the reconstruction error is defined as

whereNrepresents the number of reconstruction points,is the theoretical pressure, andis the reconstructed pressure.The reconstruction errors by the conventional method and the proposed method are 29.38%and 12.75%for the parallel case,respectively, while the reconstruction errors are 30.52% and 10.46% for the perpendicular case, correspondingly. Therefore, the performance of the conventional method is not as good as that of the proposed method, and this is because the conventional method is affected by the singular problem.Here, the minimum magnitudes of the wavenumber component inzdirection for the conventional propagators and the proposed ones are calculated,which can indicate the singularity. The values are 0.09 and 2.81 for the parallel case,respectively, and the values are 0.16 and 0.75 for the perpendicular case, respectively. Obviously, the values for the conventional propagators are close to zero in both cases,which could result in singular problem, while the values for the proposed propagators are much larger, which can effectively suppress the singularity.

Fig. 3. The pressures on the reconstruction plane for the parallel case at 1500 Hz: the theoretical pressure (a), the reconstructed pressure by the conventional method (b), and the reconstructed pressure by the proposed method(c).

Fig.4. The pressures on the reconstruction plane for the perpendicular case at 1500 Hz: the theoretical pressure (a), the reconstructed pressure by the conventional method (b), and the reconstructed pressure by the proposed method(c).

In the following,to analyze the influences of the flow velocity to the reconstruction results,the reconstruction errors at a variety of Mach numbers are calculated. The effective flow velocity for analysis is related to the analyzed frequency and the measurement spacing. The parameters other than Mach number are the same as above. According to Eq. (30) in Ref. [7], under the current setup, the range of Mach number is determined to be from 0 to 0.5, with an interval of 0.05.The reconstruction errors at different Mach numbers for the parallel case and perpendicular case are shown in Fig.5.

Fig.5. The reconstruction errors at different flow velocities by the proposed method (solid line) and by the conventional method (dashed line) for the parallel case(a)and perpendicular case(b).

For the parallel case,as shown in Fig.5(a),it can be seen that the reconstruction errors by the proposed method are at a low level(within 15.6%)and stable at different Mach numbers. In contrast, although the reconstruction errors by the conventional method are similar to the errors by the proposed method at most Mach numbers, it is unstable and has a sudden increase atM=0.3,where the error is almost two to three times that at other Mach numbers.The reason is that the singularity atM=0.3 is much stronger than the singularity at other Mach numbers, leading to larger reconstruction errors. For the perpendicular case, from Fig. 5(b) it can be found that,the reconstruction errors by the proposed method are satisfactory and stable, less than 12.5% in the range of the analyzed Mach numbers. However, the reconstruction error by the conventional method increases rapidly as the flow velocity increases, which is also caused by the singular problem.The minimum magnitudes of the wavenumber component inzdirection for the conventional propagators and the proposed ones at the analyzed Mach numbers are shown in Fig. 6. It can be found from Fig. 6(a), in the parallel case, the value for the conventional propagator atM=0.3 is much closer to zero than those at other Mach numbers, resulting in singular problems, which is consistent with the results of reconstruction errors. From Fig.6(b),in the perpendicular case,it can be seen that the value for the conventional propagator decreases as the Mach number increases, especially the values at Mach numbers greater than 0.2 are close to zero, leading to larger reconstruction errors. In addition, it can be observed that the reconstruction error by the conventional method in the perpendicular case is seemingly more sensitive to the singularity thanthat in the parallel case.This is presumably due to that in NAH procedure the normal particle velocity on the hologram plane is used as the input, and that the particle velocity in the flow direction is more affected by the flow effects than the particle velocity in directions perpendicular to the flow direction. It is concluded that the reconstruction errors by the conventional method can be amplified at different flow velocities,while the reconstruction errors by the proposed method can keep stable at a low level,whether in the parallel case or the perpendicular case.

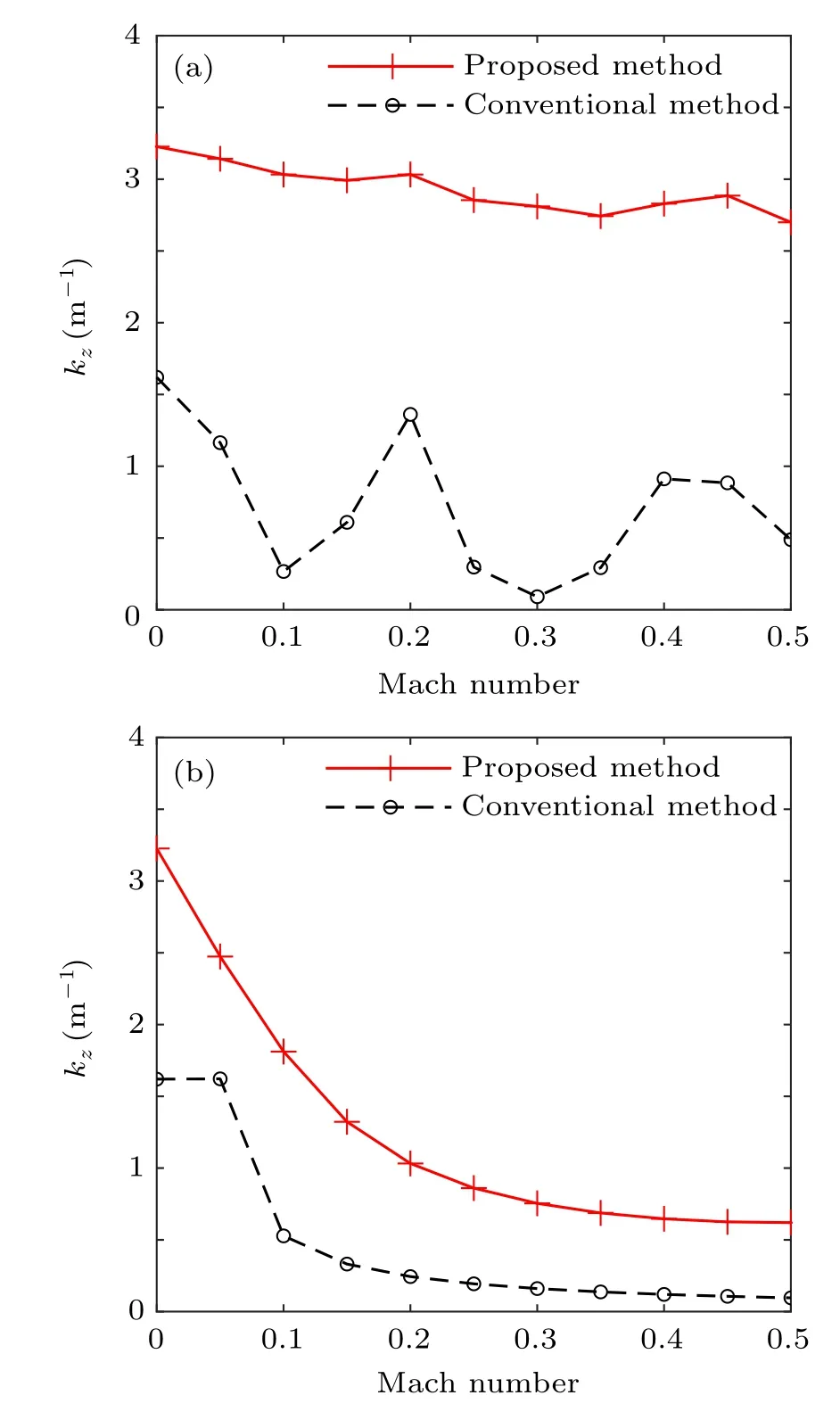
Fig. 6. The minimum magnitudes of the wavenumber component in z direction at different Mach numbers for the proposed method(solid line)and conventional method(dashed line)in the parallel case(a)and perpendicular case(b).

Furthermore, the performance of the proposed method and the conventional method at different frequencies are tested whenM=0.3. The flow effects will change the effective frequency range for NAH. According to Eqs. (45) and (46) in Ref. [6], here the analyzed frequency range is determined to be from 400 Hz to 2500 Hz, with an interval of 100 Hz. The reconstruction errors by the proposed method and the conventional method at different frequencies for the parallel case and perpendicular case are presented in Fig.7.

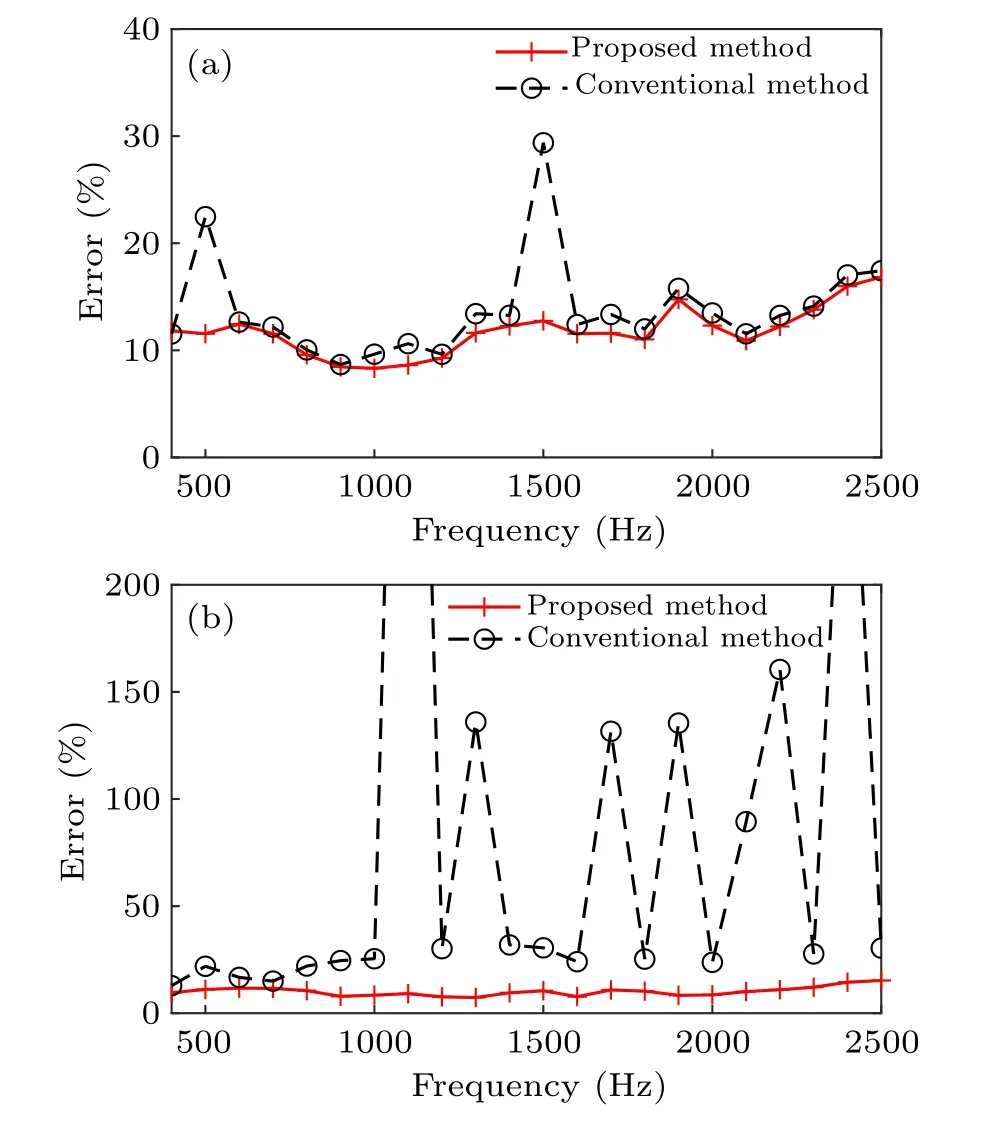
Fig. 7. The reconstruction errors at different frequencies by the proposed method (solid line) and by the conventional method (dashed line) for the parallel case(a)and perpendicular case(b).

As shown in Fig.7(a),for the parallel case,it can be seen that the reconstruction errors by the proposed method are stable and at a low level,within 16.9%in the analyzed frequency range. Comparatively, the reconstruction errors by the conventional method have considerable increases at 500 Hz and 1500 Hz, due to that the singularity at these two frequencies is much stronger than that at other frequencies. For the perpendicular case, from Fig. 7(b), it can be observed that the reconstruction errors by the proposed method keep stable,less than 15.3%at different frequencies. However,the reconstruction errors by the conventional method have severe fluctuations, and the reconstruction errors at some frequencies are close to or exceed 100%, such as 602.56% at 1100 Hz and 332.78%at 2400 Hz. It should be noted that,to make the lines in the figure clearer,the errors are only displayed within 200%.The minimum magnitudes of the wavenumber component inzdirection for the conventional propagators and the proposed ones at the analyzed frequencies are shown in Fig. 8. It can be observed that the values at some frequencies are close to zero in both parallel case and perpendicular case,which indicates that there are greater reconstruction errors at these frequencies due to singular problems. In fact, as for the cases with large errors,the reconstruction results will be completely wrong, which means the conventional method would be invalid at these frequencies. The reconstructed pressures on the reconstruction plane by the proposed method and the conventional method for the perpendicular case at 1300 Hz are shown in Fig.9.

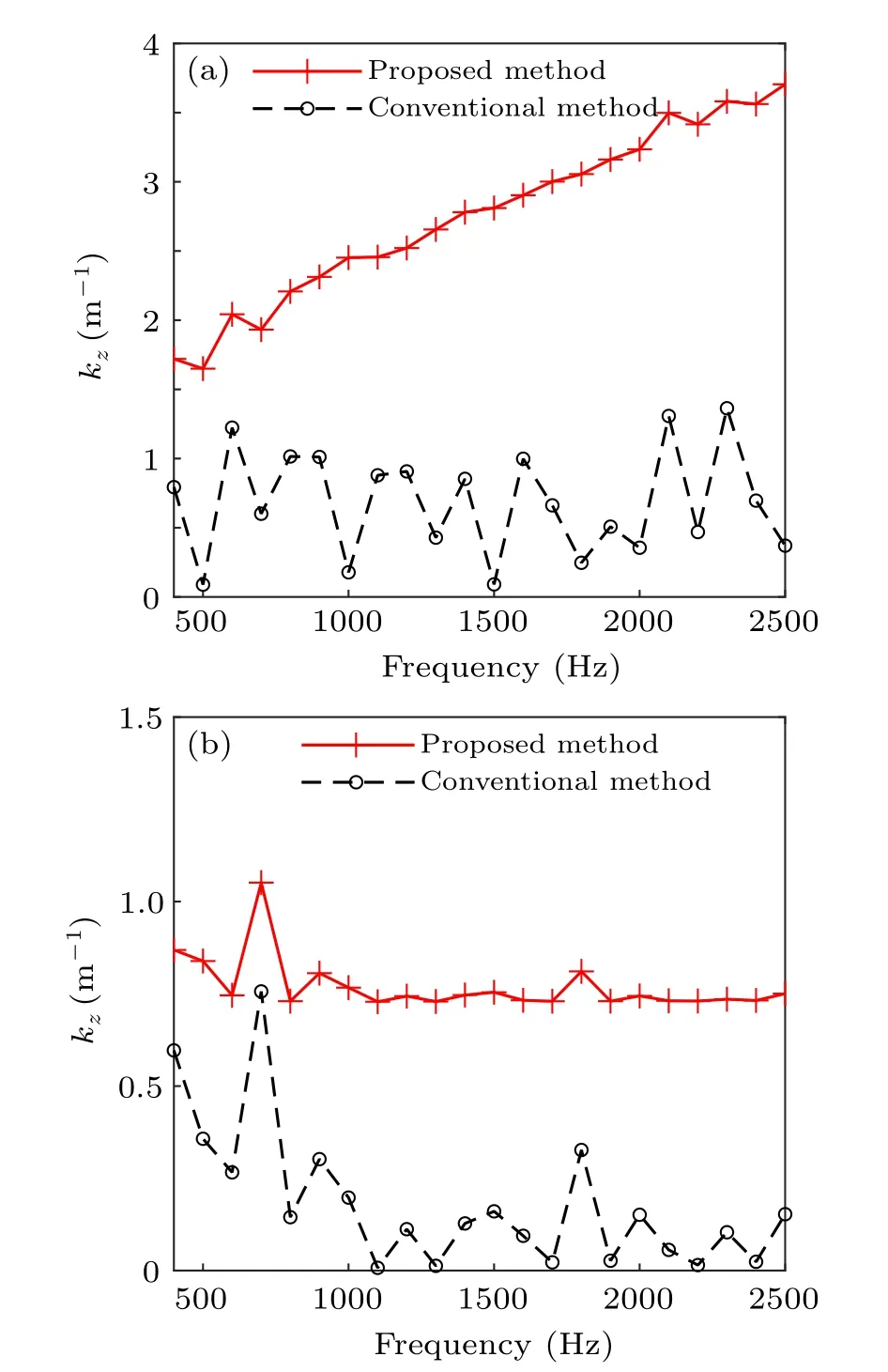
Fig.8. The minimum magnitudes of the wavenumber component in z direction at different frequencies for the proposed method (solid line) and conventional method (dashed line) in the parallel case (a) and perpendicular case(b).

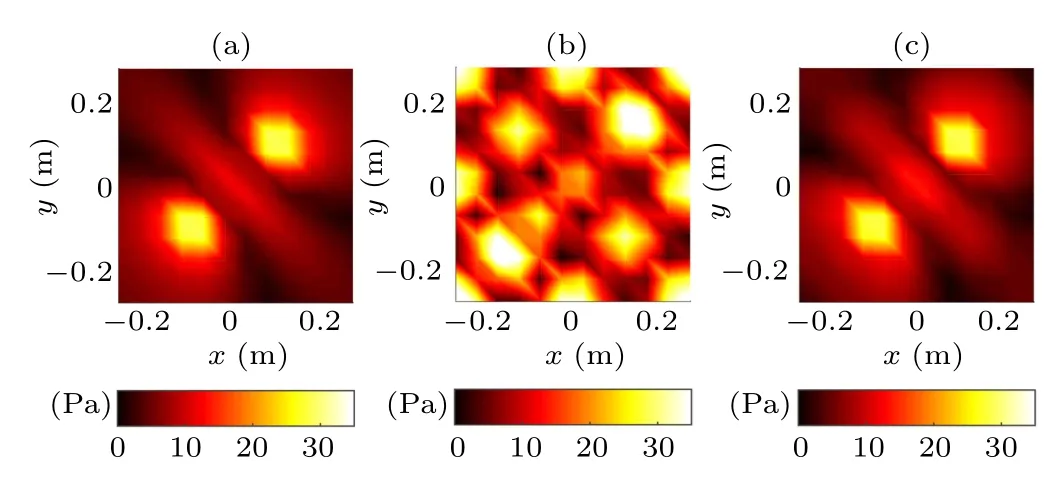
Fig.9. The pressures on the reconstruction plane for the perpendicular case at 1300 Hz: the theoretical pressure (a), the reconstructed pressure by the conventional method (b), and the reconstructed pressure by the proposed method(c).

From Fig.9,it can be seen that the sound field distribution on the reconstruction plane by the conventional method is totally different from the theoretical one,and the two monopoles cannot be recognized any more. In contrast, the pressure reconstructed by the proposed method agrees with the theoretical one very well, including the sound field distribution and the amplitude level. The reconstruction errors by the proposed method and the conventional method are 7.33% and 135.95%,respectively.The reason for this phenomenon is that there is a strong singularity for the conventional method,while the singularity can be effectively suppressed for the proposed method. To illustrate it better, the conventional velocity-topressure propagator and the proposed one alongky=−0.6614 are given in Fig.10. It can be found that there are two singular points for the conventional propagator alongky=−0.6614 ,where the magnitudes are up to 0.77×106, while the magnitudes at the same points are 1.4×104for the proposed propagator. That is to say, the magnitudes at the two points for the proposed method is smaller than that for the conventional method by nearly two orders. Therefore,the proposed method can realize an accurate reconstruction.

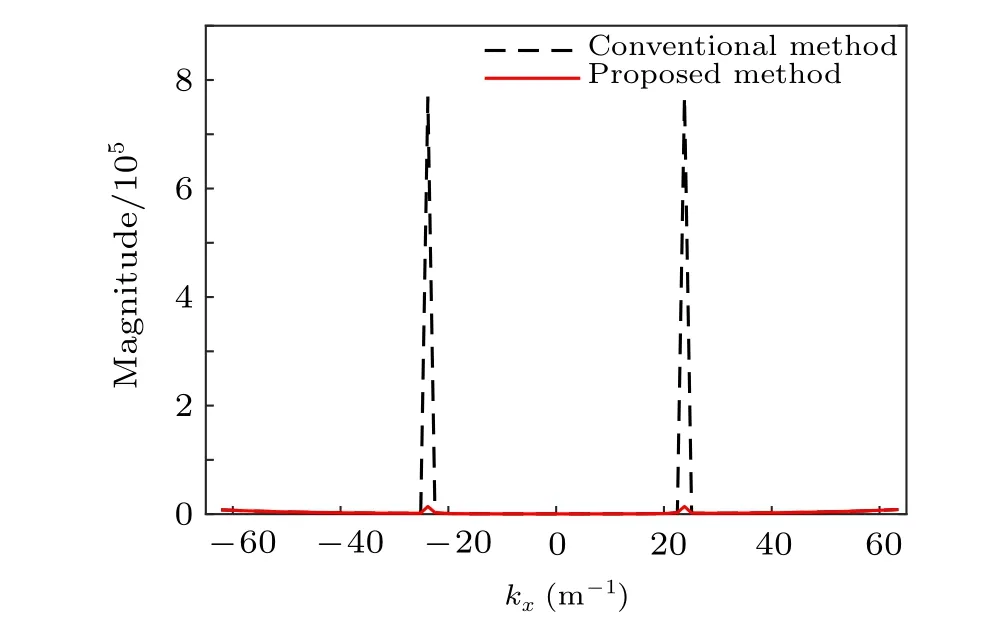
Fig. 10. The conventional and proposed propagators for the perpendicular case at 1300 Hz along ky=−0.6614.

To examine the influence of background noise,the performance of the proposed method and the conventional method under condition of different SNRs are conducted. Here, the SNR spans from 0 dB to 30 dB,with an interval of 5 dB.The Mach number is set to be 0.3, and the frequency is 1500 Hz.The reconstruction errors by the proposed method and conventional method with the analyzed SNRs for parallel case and perpendicular case are given in Fig.11.It can be observed that although the reconstruction errors by the conventional method can keep relatively stable under the condition of SNRs higher than 10 dB, the reconstruction error increases apparently for SNRs lower than 10 dB in both parallel case and perpendicular case. In contrast, the reconstruction errors by the proposed method is insensitive to noise in the range of the analyzed SNRs, and the errors are at a low level (within 14%)for both the parallel case and perpendicular case. The reason is that the background noise is not over-amplified by the proposed method in reconstruction process,since the singular problem associated with extremely high magnitudes of conventional propagators at some wavenumber components are suppressed effectively, and the wavenumber-domain convective low-pass filter is used as well.

Based on the above analysis in this section, it can be found that the singular problem could result in significant reconstruction errors for the conventional method in both parallel case and perpendicular case,although sometimes the reconstruction errors by the conventional method are similar to those by the proposed method when the singularity is weak.The singularity is related to the flow velocity and the frequency, and in practice it is difficult to predict and avoid the singularity for the conventional method. Owing to the deduced nonsingular velocity-to-pressure propagators, the proposed method can realize accurate reconstruction, whether in the parallel case or the perpendicular case.

Fig.11.The reconstruction errors at different SNRs by the proposed method(solid line) and conventional method (dashed line) for the parallel case (a)and perpendicular case(b).

4. Conclusions

NAH in a moving medium based on particle velocity input using nonsingular propagator is presented in this paper, to realize accurate sound field reconstruction in a moving medium,such as wind tunnel applications. Two cases that the hologram plane is parallel to and perpendicular to the flow direction are analyzed. By virtue of the Laplace transform and the spatial Fourier transform,two nonsingular velocity-topressure propagators in complex-frequency wavenumber domain are derived, corresponding to the parallel case and perpendicular case.Due to the deduced propagators are presented in the complex-frequency domain instead of the frequency domain, the denominators of the propagators are always nonzero,and thus the singular problem can be resolved. Numerical simulations are conducted to examine the effectiveness and validity of the proposed method,and the conventional method is also performed for comparison. The reconstruction results show that the singular problem could result in significant errors for the conventional method, especially for the perpendicular case, the reconstruction results could be completely wrong. In contrast, the proposed method can realize accurate reconstruction at different Mach numbers,frequencies and SNRs,whether for the parallel case or the perpendicular case,which shows the proposed method is stable and valid. In addition,the selection criteria of convergence factor for NAH is worthwhile to be studied further, and the relevant researches will be done in the future.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. 11804002), the University Science Research Project of Anhui Province, China (Grant Nos. KJ2019A0792 and KJ2019A0797), and the Anhui Jianzhu University Research Project(Grant No.2018QD06).