Quantum simulation of lattice gauge theories on superconducting circuits: Quantum phase transition and quench dynamics

Zi-Yong Ge(葛自勇), Rui-Zhen Huang(黄瑞珍), Zi-Yang Meng(孟子杨), and Heng Fan(范桁),4,6,‡

1Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100190,China

3Kavli Institute for Theoretical Sciences,University of Chinese Academy of Sciences,Beijing 100190,China

4Songshan Lake Materials Laboratory,Dongguan 523808,China

5Department of Physics and HKU-UCAS Joint Institute of Theoretical and Computational Physics,The University of Hong Kong,Hong Kong SAR,China

6CAS Center for Excellence in Topological Quantum Computation,University of Chinese Academy of Sciences,Beijing 100190,China

Recently,quantum simulation of low-dimensional lattice gauge theories(LGTs)has attracted many interests,which may improve our understanding of strongly correlated quantum many-body systems.Here,we propose an implementation to approximate Z2 LGT on superconducting quantum circuits, where the effective theory is a mixture of a LGT and a gauge-broken term.By using matrix product state based methods, both the ground state properties and quench dynamics are systematically investigated.With an increase of the transverse (electric) field, the system displays a quantum phase transition from a disordered phase to a translational symmetry breaking phase.In the ordered phase,an approximate Gauss law of the Z2 LGT emerges in the ground state.Moreover, to shed light on the experiments, we also study the quench dynamics, where there is a dynamical signature of the spontaneous translational symmetry breaking.The spreading of the single particle of matter degree is diffusive under the weak transverse field,while it is ballistic with small velocity for the strong field.Furthermore,due to the emergent Gauss law under the strong transverse field,the matter degree can also exhibit confinement dynamics which leads to a strong suppression of the nearest-neighbor hopping.Our results pave the way for simulating the LGT on superconducting circuits,including the quantum phase transition and quench dynamics.

Keywords: quantum simulation,superconducting circuits,lattice gauge theories

1.Introduction

In the last two decades, with the rapid development of quantum manipulation technologies, simulating quantum physics on synthetic quantum many-body systems, termed quantum simulation,[1,2]has attracted enormous interests.Quantum simulations are expected to provide an alternative for solving problems in strongly correlated systems, which may be much challenging by the traditional methods.Meanwhile, quantum simulations have also greatly enriched the study of quantum physics, especially the out-of-equilibrium dynamics of quantum many-body systems.[3,4]There are various platforms for performing quantum simulations, such as ultracold atoms, trapped ions, nuclear spins, and superconducting circuits.Among them, superconducting circuits[5,6]are believed to be one of the most competitive candidates for achieving the universal quantum computation,due to the scalability,long coherent time,and high-precision control.Specifically, each superconducting qubit can be precisely and simultaneously addressed under arbitrary bases.Thus, it is believed that the superconducting circuit platform is another good choice to perform quantum simulations of challenging quantum many-body physics,and recently,there are many experiments about simulating the dynamics of quantum manybody systems in superconducting circuits.[7–18]Furthermore,the quantum supremacy[19–21]has been demonstrated on a superconducting processor.

Lattice gauge theories (LGTs) are originally proposed to understand the confinement of quarks.[22]In addition to high energy physics,LGTs also play a significant role in condensed matter physics.[23–27]In low-dimensional condensed matter systems, gauge fields can emerge due to the strong quantum fluctuation.For instance, the emergent gauge fields are closely related to the quantum spin liquid[28]and deconfined quantum critical point.[29]Recently, the real-time dynamics[30,31]and quantum simulations of LGTs have drawn much attention from both theoretical and experimental physicists.The corresponding schemes have been proposed in terms of ultracold atoms,[32–34]trapped ions,[35]specific superconducting circuits,[36,37]and other digital/analogue quantum circuits.[38,39]Some of these schemes have been realized in ultracold atoms experimentally.[40–42]Nevertheless, it is still a challenge to study LGT on superconducting circuits experimentally,and the key problem is how to design a feasible scheme for realizing a LGT Hamiltonian.

In this work, we focus on the one-dimensional (1D) superconducting quantum circuits.[5,6]Applying stagger longitudinal(z-directional)and transverse(x-directional)fields,we obtain an effective Hamiltonian containing a Z2LGT and a gauge-broken term.The transverse field can induce a quantum phase transition(QPT)from a gapless disorder phase to a translation-symmetry breaking the dimer phase.Despite lacking Z2gauge structure for the whole Hamiltonian,an approximate Gauss law can still emerge in the ground state of dimer phase.Furthermore,inspired by the experiment,we also study the real-time dynamics,during which there is a dynamical signature of translational symmetry breaking.We find that the particle of matter degree can diffuse to the whole system under weak transverse fields after a quantum quench.However,in the case of strong transverse fields, it displays a ballistic propagation.Moreover, the nearest-neighbor (NN) hopping almost disappears, which is a strong dynamical signature of confinement induced by the emergent approximate Gauss law.

2.The model

Here we consider a superconducting quantum processor containing 2Lqubits arranged into a chain, see Fig.1(a),where the Hamiltonian of this system is the 1D Bose–Hubbard model.[11,14,16]The on-site interaction of this Bose–Hubbard model originates from anharmonicity of each qubit, which is much larger than the NN coupling strength,[11,14,16]so the Fock space of each qubit can be truncated to 2.Thus,the system can be described by an isotropic 1DXYmodel,of which the Hamiltonian reads[11,14,16]

To implement Z2LGT,we let the local potentials at odd and even qubits be Δ and λ,respectively,and let detuning between two NN qubits much larger than the coupling strength,i.e., |Δ −λ|≫J.In addition, the transverse field is only applied on the even qubits with equal strengthh, see Fig.1(b).Therefore,the Hamiltonian(1)can be simplified as

where Δ ≫J,λ,h.

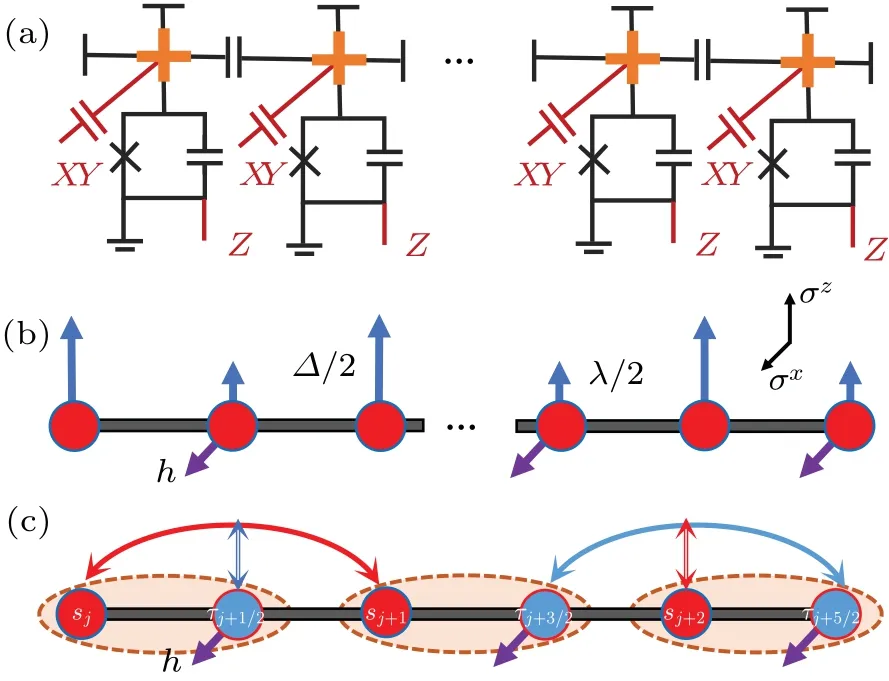
Fig.1.(a)The diagram of 1D superconducting quantum circuits.The nearest-neighbor two qubits are coupled capacitively, and each qubit contains a Z bias line and an XY driven line,which can be used to control the frequency and transverse field,respectively.(b)Lattice diagram of Eq.(2).The strengths of longitudinal fields are Δ/2 and λ/2 for the odd and even sites, respectively.The transverse field is only applied on the even sites with the strength h.(c) Lattice diagram of Hamiltonian(3).The odd and even qubits are labeled by s(red sites)and τ(blue sites),respectively.The arrow represents the three-body coupling,and sj and compose an unit cell(dashed orange circles).

Using Schrieffer–Wolff transformation,[43,44]we can obtain an effective Hamiltonianwritten as

3.Ground-state phase diagram

We use density matrix renormalization group (DMRG)method[46,47]to study the ground-state properties of.Here,we fix the couplingge=1,sethas the driving parameter,and only considerh>0.Open boundary condition is used for the numerical simulation.Furthermore, we set thesspins to be half-filling,i.e.,=0.In the numerical calculation,we choose the max bond dimension up to 600 with truncation error smaller than 10−7.Furthermore, we adopt careful finite truncation error analysis to obtain more accurate results.The details of our numerical method are shown in supplementary materials.

Whenh=0,describes the free gapless fermions after the Jordan–Wigner transformation.We expect the system belongs to Luttinger liquid at smallh.The transverse field term serves as a relevant perturbation and may induce a gap.Indeed, from the numerical simulation, we find that there is a QPT and the translational symmetry is spontaneously broken at largeh.Here, to probe translational symmetry broken, we calculate the local energy densityEj:=,where

and〈·〉represents taking expectation value towards the ground state.As shown in Fig.2(a), the local energy density in the bulk retains translational invariance for smallh, while it becomes dimerized in the largehregion.It can also be reflected by the polarization of, see Fig.2(b).This reveals that the condensation ofinduces a π momentum,which breaks the translational invariance.

Next, we use finite-size scaling to determine the critical properties.From Fig.2(c), we can find that+H.c.is the other term breaking the translation invariance.Thus,we choose the order parameter as the expectation value difference of the operatorbetween odd and even bonds.To avoid the boundary effect,we only consider the central two bonds,i.e.,the order parameter εd:=.At the critical pointh=hc, εdsatisfies a power law with respect to the system sizeL, i.e., εd|h=hc～L−Δε.According to Fig.2(d), we determine the critical point to behc=1.245 and Δε≈0.23.To double check the accuracy of our calculation,we construct the dimensionless quantity εdLΔεand find it indeed crosses athcfor different sizes as shown in Fig.2(e).Then from the data collapse of the order parameter we obtain the exponent 1/ν ≈0.62,see Fig.2(f).We also study the correlationGΨ(j−i)=(has the same dimension as).As shown in Figs.2(g)and 2(h),GΨ(r)exhibits a power-law decay athcwith the exponent η ≈0.46 which is consistent with η=2Δε.In supplementary materials,we present the additional numerical results of the correlation function away from the critical point.

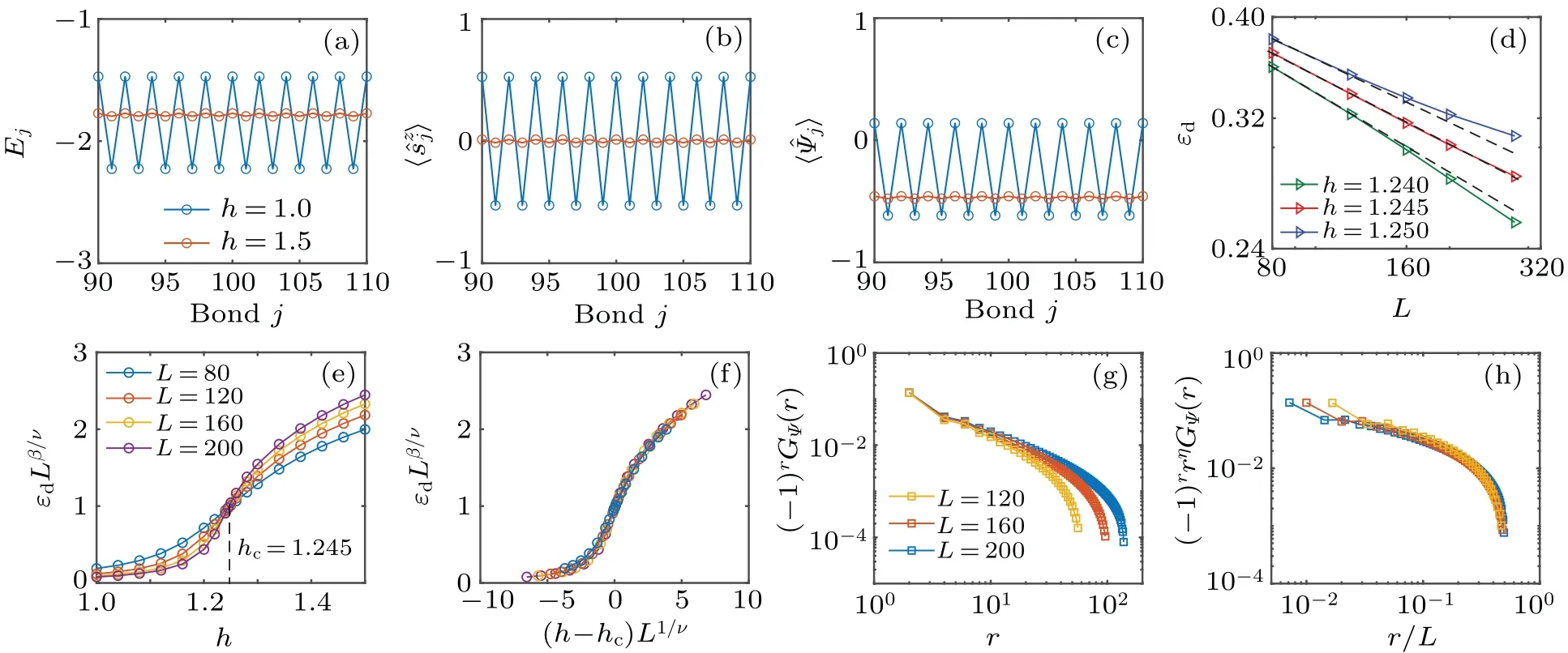
Fig.2.The distribution of(a)Ej,(b),and(c) in the ground state with L=200.(d)The function between εd and system size L.At the critical point h=hc=1.245,εd ～L−Δε ～L−0.23.The dashed black lines are the linear fittings.(e)Rescaled εdLΔε as the function of h for different system sizes.The curves are across at the critical point.(f)The data collapse of(e)with 1/ν ≈0.62.(g)The correlation functions GΨ(L/2−r,L/2)for different system sizes at the critical point.(h)The data collapse of(g)with η ≈0.46.

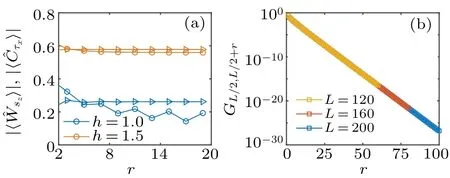
Fig.3.(a) The expectation values of (circle) and (triangle) in the ground state with L=80 for h=1 and h=1.5, respectively.To avoid the boundary effect,we calculate these two objects at the cell interval[L/2 −r/2+1,L/2+r/2].(b)The gauge invariant correlation function GL/2,L/2+r.

4.Quench dynamics

In quantum-simulation experiments, preparing the ground state ofis much challenging.Instead, it is more convenient to study the quench dynamics.Therefore, we expect that the above ground-state properties can be probed by the dynamical behaviors, which may be realized in future experiments.Here, we use time evolving block decimation(TEBD) method[46–48]under the open boundary condition to study the real-time dynamics of.Here, we choose the second-order Suzuki–Trotter decomposition and the max bond dimension up to 400.Furthermore, we also enlarge the maximum bond dimension and decrease time of single step till the final results converge.The details of our TEBD methods are presented in supplementary materials.We consider the dynamics in thessector during the quench process and set the totalscharge to=1.The initial state is chosen as |ψ0〉 = |s〉⊗|τ〉, where |s〉 = |···↓↓↑↓↓···〉 and|τ〉=|···←←←···〉.That is,for thessector,only the central cell is spin-up,and all τ sites are at the ground state of ˆτx,i.e.,).We calculate the time evolution of the density distributions of matter field ρj(t):=,where|ψ(t)〉=.

We firstly study the case of small transverse fields.We find that thescharge can spread to the whole system after a quantum quench as shown in Fig.4(a).To pursue how thescharge spreads, we calculateR(t)=,[49]which is the average distance to the initial position for thescharge.As demonstrated in Fig.4(b), one can find thatin the intermediate-time regime, wheret0is a time shift resulted from the relaxation at the beginning.Thus,the spreading of thescharge is diffusive after a quick relaxation under the weak transverse field.In fact,the initial state,in this case, is far away from the ground state, which makes the system thermalize.Therefore,the τ sector can be considered as a random scatting potential of thessector after the relaxation leading to a diffusive spreading ofscharge.

For the large transverse field, the propagation of thescharge is very different.Whenh=2, as shown in Fig.4(c),one can find that thescharge exhibits a light-cone-like spreading at long time rather than diffusion.In the case of a strong transverse field,the system locates a low-energy regime during the quench dynamics, so that the system fails to thermalization.Therefore, thescharge cannot exhibit a diffusive transport.The detailed phenomenological discussion about these two distinct spreading types between small and large transverse fields can be found in supplementary materials.In addition, we can also find that the corresponding propagation velocity is much smaller than that for theh=0 case (in this case, the effective Hamiltonian isXYmodel, so the velocity is about 2ge[14]).Meanwhile, the hopping of thesspin between NN cells is strongly suppressed, although there only exist NN hopping terms ofsspins in the effective Hamiltonian.Instead,thesspin almost exhibits a next-nearest-neighbor(NNN)hopping.In the following discussion,we will demonstrate that this suppression of NN propagationsspin is closely related to the confinement induced by emergent gauge invariance.Furthermore,we also present the curves ofR(t)for differenthin Fig.4(d).One can find there is a clear transition from diffusive to ballistic spreading aroundh=1.3 which is close tohc.Therefore,the spreading ofsprovides a dynamical signature of the spontaneous translational symmetry breaking.

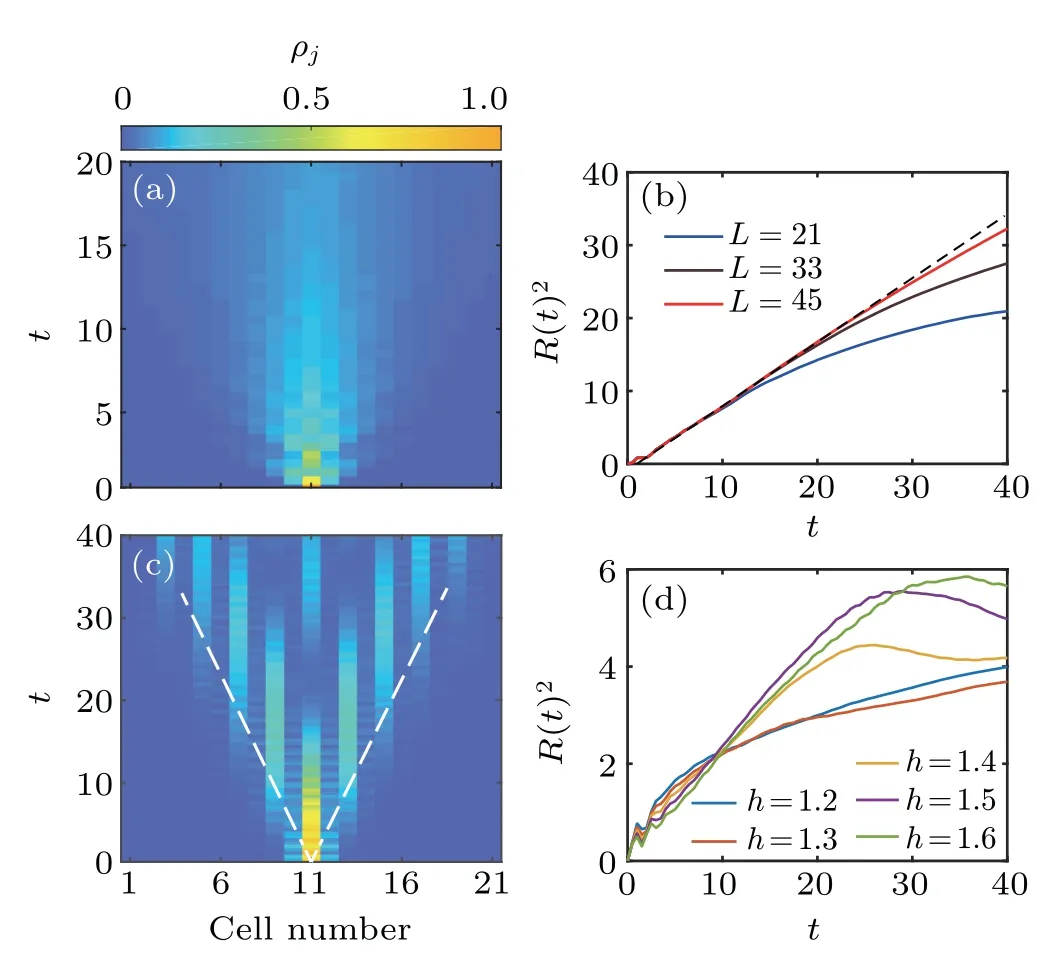
Fig.4.(a)The time evolution of ρ j for h=1 and L=21.(b)The curves of R(t)2 for h=1 with different system sizes.The black dashed line is a linear fitting.(c)The time evolution of ρj for h=2 and L=21.(d)The curves of R(t) for different transverse field strength with L=21.There is a sharp transition around h=1.3.

We further pursue the relation between the emergent approximate Gauss law and the anomalous spreading ofscharge after a quantum quench.Clearly, without the gauge breaking term ˆH2, the hopping ofscharge is accompanied by the flip of τ spin between|→〉and|←〉,leading to the energy change of 2h, see the first and second steps in Fig.5(a).Thus, thescharge is confined and localized under non-zero transverse fields,[40,45]as shown in Fig.5(b).

However, what is the fate of this confinement when adding a gauge-violation term? Here,contains the gauge violation term.This term can flip two NN τ spins between |→〉 and |←〉.Thus, as shown in Fig.5(a), under the role of,the system can firstly have two imaginary processes to make asspin hop to the NNN cell by flipping two τ spins.Then,these two τ spins can flip back through the term.Here,this whole process does not violate the energy conservation and thus is a real process.This is the phenomenological mechanism why thescharge can only emerge NNN hopping for largeh,and the compression of NN hopping of thescharge can be considered as the effect of confinement induced by emergent Gauss law.From Figs.4(c)and 5(b),we can find that, in the early time scalet≤6, the dynamics ofHfis almost the same as the pure gauge-invariant model.At a much larger time scalet>10, the higher-order process which violates the emergent gauge invariance contributes,and the NNN spreading dynamics recovers.

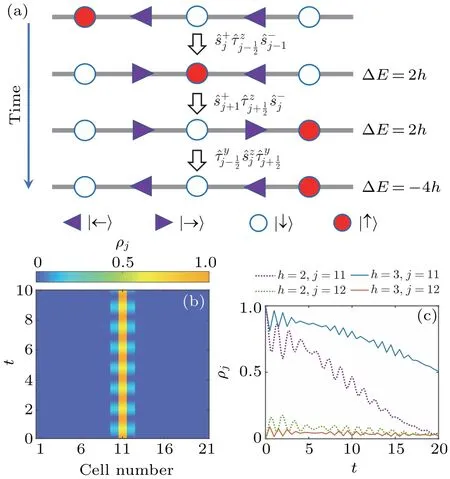
Fig.5.(a)Schematic diagram of the propagating of s spin.(b)The time evolution of ρj for ˆH1 with h=2,which is consistent with the result in Ref.[40].(c)The curves of ρj(t)for ˆHf dynamics with h=2 and h=3.The initial state is the same as the one in Fig.4.

To further support the analysis, we also present the density distribution near the center unit cell for a largerhin Fig.5(c).Indeed the spreading becomes much weaker for a largerh,in which the confinement effect is stronger.Note that in the experiments,the initial time stage is the most accessible,therefore,one can observe strong signals for the confined(localized) dynamics.These results demonstrate that the emergent approximate Gauss law and confinement can indeed be witnessed by the quench dynamics.

5.Summary

We have constructed an effective model on the superconducting circuits, which is the mixture of a Z2LGT and a gauge-broken term,and systematically studied the QPT and quench dynamics.We found that this system can exhibit a QPT from a disorder phase to a dimer phase with the increase of the transverse field.Moreover, an approximate Gauss law can emerge for the largehregime,and the dimer state can be regarded as a confinement phase as an analogy to the LGT.This QPT can also be probed by the spreading of the matter particle during the quench dynamics.It displays a transition from diffusive to ballistic spreading with an increase of the transverse field.Remarkably,the quench dynamics for the largehcan be explained from the confinement viewpoint.Our work may inspire the future study of LGTs from the dynamical viewpoint.Meanwhile,our results lay the foundation for the further quantum simulation of 2D LGTs related problems on superconducting circuits.

In Refs.[36,37], two schemes of implementing 1D and 2D quantum link models on the specific superconducting circuits were proposed, respectively.Comparing with these two works,our scheme is based on the conventional 1D superconducting circuits and manipulation technologies and is more accessible in experiments based on the state-of-the-art experimental technologies.[7–18]On the other hand, the realization of the effective model in this work is distinct from that in cold atoms,of which gauge fields are realized by the densitydependent tunneling matrix.While in our proposal,the matter field(τ)and gauge field(s)are directly realized by the odd and even qubits, respectively.Finally, there still exist many other open questions.For instance, the microscopic mechanism of the emergent gauge invariance is still not clear,and it deserves further study via careful bosonization like techniques.The thermalization of this system is also believed to be an interesting topic, and another meaningful issue is whether we can realize a truly gauge-invariant Hamiltonian on superconducting circuits.

Acknowledgements

The DMRG and TEBD calculations are carried out with TeNPy Library.[50]R.Z.H is supported by China Postdoctoral Science Foundation (Grant No.2020T130643), the Fundamental Research Funds for the Central Universities,and the National Natural Science Foundation of China(Grant No.12047554).Z.Y.M acknowledges support from the National Key Research and Development Program of China (Grant No.2016YFA0300502) and the Research Grants Council of Hong Kong SAR China (Grant No.17303019).H.F acknowledges support from the National Key R&D Program of China (Grant Nos.2016YFA0302104 and 2016YFA0300600),the National Natural Science Foundation of China(Grant Nos.11774406 and 11934018),Strategic Priority Research Program of Chinese Academy of Sciences(Grant No.XDB28000000), and Beijing Academy of Quantum Information Science(Grant No.Y18G07).