Channel parameters-independent multi-hop nondestructive teleportation

Hua-Yang Li(李华阳), Yu-Zhen Wei(魏玉震), Yi Ding(丁祎), and Min Jiang(姜敏),3,†

1School of Electronics&Information Engineering,Soochow University,Suzhou 215006,China

2School of Information Engineering,Huzhou University,Huzhou 313000,China

3Key Laboratory of System Control and Information Processing,Ministry of Education,Shanghai 200240,China

A multi-hop nondestructive teleportation scheme independent of channel parameters based on Bell pairs is presented,where the coefficients of the quantum channel are unknown to all the communication nodes.With Bell measurement and channel matching technology the unknown channel parameters can be eliminated probabilistically with the help of the intermediate nodes.Then the source node Alice can teleport an unknown state to the remote destination node Bob.In our scheme the teleportation is generalized first to the scenario independent of channel parameters, which makes the requirement of quantum channel reduced.Our scheme still preserves the initial unknown state even if this teleportation fails.Moreover,performance analysis shows that our scheme has a higher communication efficiency.

Keywords: multi-hop quantum communication,entanglement swapping,teleportation

1.Introduction

Quantum teleportation(QT)is an important and interesting task which has recently attracted much attention because of its promising applications in the field of secure quantum communication and quantum computing.In a teleportation protocol,an unknown quantum state can be recreated at a distant location by exploiting shared entanglement and classical communication between the sender and the receiver.In 1993, Bennettet al.[1]first proposed the standard quantum teleportation to teleport an arbitrary single-qubit state based on the maximally entangled Bell state, which was verified experimentally by Bouwmeesteret al.[2]After that, lots of QT schemes were presented with different quantum technologies.For example, the QT schemes based on EPR pairs,[3–5]GHZ states,[6,7]W states,[8–10]cluster states,[11–13]mixed states,[14,15]and continuous-variable states[16]have been proposed.Nevertheless, in the actual quantum communication,it is difficult to establish the direct entanglement between the sender and the remote receiver on account of inevitable losses on the quantum channel.

Recently,quantum teleportation network based on entanglement swapping,[17–19]which aims to establish the entanglement between two distant nodes via intermediate nodes,has become a research hotspot.In a multi-hop chain, there are available entangled channels between adjacent nodes.It is possible that quantum channels could be built to transmit the unknown state between the source and the destination node.In 2013, Yuet al.proposed a routing protocol for a wireless ad hoc quantum communication network.[20]In 2014,Wanget al.devised a quantum wireless multi-hop teleportation scheme based on arbitrary Bell pairs.[21]In 2015,Shiet al.proposed a quantum wireless multi-hop network in which an arbitrary single qubit could be teleported hop by hop based on shared Werner states.[22]In 2016, Xionget al.proposed a multi-hop teleportation protocol of partially entangled GHZ state, with the help of auxiliary particles.[23]In 2017, Zouet al.presented a multi-hop teleportation scheme of two-qubit state via the composite GHZ-Bell channel.[24]Unfortunately,owing to the inevitable couplings between the quantum states and their surroundings,the maximally entangled channel readily evolved into the non-maximally entangled channel,[25,26]which brings the risk of data loss.[27]In order to avoid possibly destructing the unknown state to be teleported, some improved schemes were reported by establishing the faithful channel beforehand.[28–31]

However, in the above QT schemes, the partially entangled state is used most widely as the quantum channel.In these schemes,the sender or the receiver needs to know the parameter information of the entangled channel completely.Then he introduces an auxiliary particle and adopts a joint unitary transformation which is related to the channel parameters to reconstruct the initial state.Considering the fact that the quantum teleportation may occur in the situation where the channel parameters cannot be known to all communication participants, we firstly propose a multi-hop nondestructive teleportation scheme independent of the channel parameters based on Bell pairs, where the coefficients of quantum channel are unknown to all communication participants to reduce the requirements for quantum channel.With the Bell measurement performed by the intermediate nodes, the unknown parameters of the Bell pairs can be eliminated probabilistically.Then the source node and the destination node can establish a maximally entangled Bell channel.The unknown state can be recovered by the destination node Bob or preserved by source node Alice.Besides the performance analysis shows that our scheme has a higher communication efficiency.

The rest of this paper is organized as follows.In Section 2 a basic two-hop nondestructive teleportation scheme is described based on two Bell pairs where the coefficients of quantum channel are unknown to all communication participants.Then the construction rule of the direct Bell channel shared by two communication nodes in a multi-hop chain composed of Bell pairs is introduced.In Section 3 a multi-hop nondestructive teleportation scheme independent of channel parameters based on channel matching is presented.In Section 4, the performance of our scheme is analyzed.Finally,some conclusions are drawn in Section 5.

2.Preliminaries

In this section, a basic two-hop nondestructive teleportation scheme is first introduced based on the two Bell pairs where the coefficients of quantum channel are unknown to all communication participants,which is described in Subsection 2.1.Then the construction rule of the direct Bell channel finally shared by two communication nodes in a chain composed of Bell pairs is discussed in Subsection 2.2.

2.1.Two-hop nondestructive teleportation scheme

Without loss of generality, the source node Alice is assumed to want to teleport an unknown arbitrary single-qubit|γ〉tto the destination node Bob who does not share direct entanglement with Alice and|γ〉tcan be written as

wherea1anda2are complex and satisfy the normalization condition|a1|2+|a2|2=1.

The intermediate node Cindy shares one Bell pairwith Alice and another onewith Bob, which can be expressed as

whereb1andb2are the channel parameters that satisfy the normalization condition|b1|2+|b2|2=1, and they are unknown to all communication participants.

As shown in Fig.1,Alice owns particlestandA1.Cindy owns particlesB1andA2,and Bob owns particleB2.The initial quantum state of the whole system reads

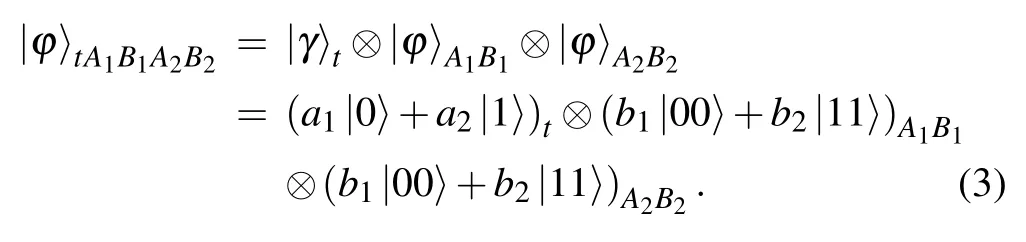
Fig.1.Qubit distribution of two-hop nondestructive teleportation.

To teleport|γ〉tfrom Alice to Bob,three participants will perform a series of operations in three steps, as shown in Fig.2.

Step 1Alice performs one CNOT gate on her own particlestandA1,and then performs oneHgate on her particlet.The CNOT gate can be expressed as

TheHgate can be described as

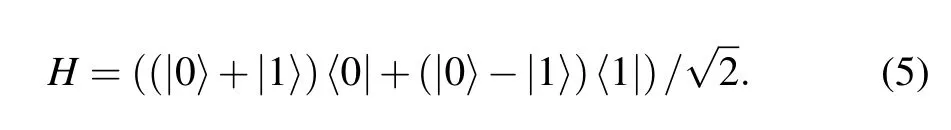
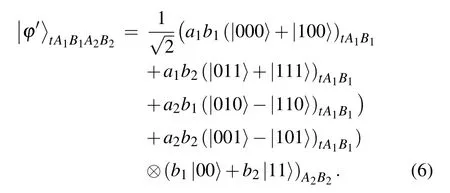
Step 2The statein Eq.(6)can be written as

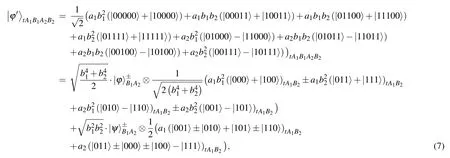
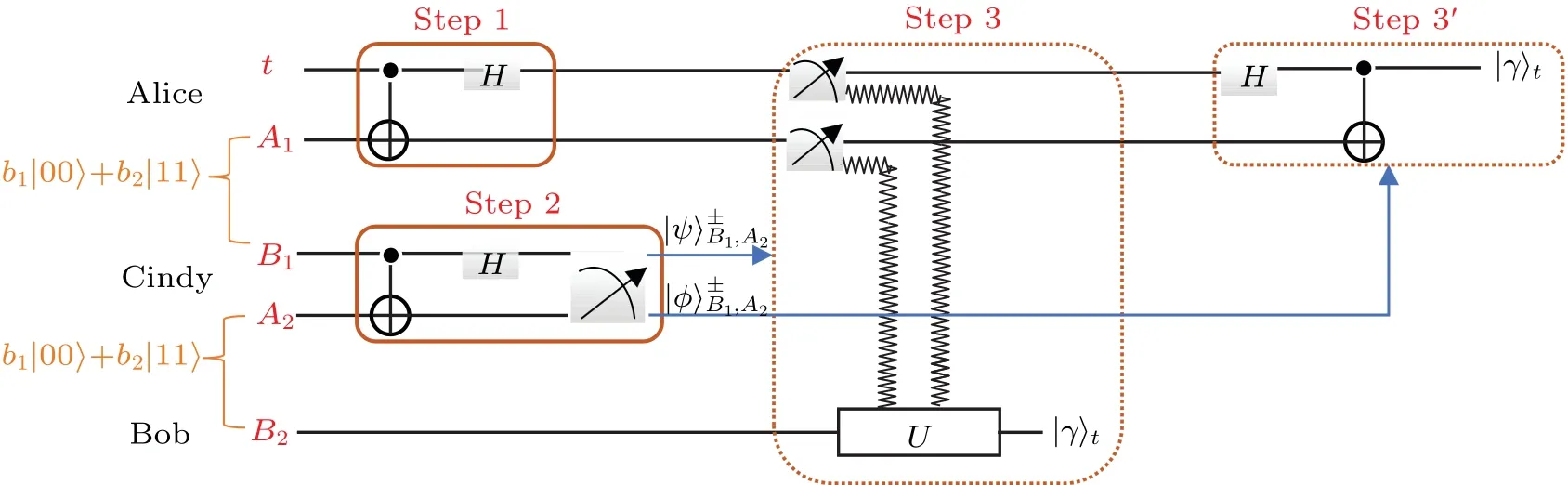
Fig.2.Quantum circuit for two-hop nondestructive teleportation with two Bell channels.

It is obvious that no unknown channel parametersb1andb2exist in Eq.(8).Next, Alice performs one projection measurement on her two particlestandA1with the basis{|00〉,|01〉,|10〉,|11〉}.According to the measurement result sent by Alice, Bob can perform the corresponding unitary operation(one of four Pauli matrices:I=|0〉〈0|+|1〉〈1|,Z=|0〉〈0|−|1〉〈1|,X=|0〉〈1|+|1〉〈0|,XZ=|0〉〈1|−|1〉〈0|)on particleB2to recover the original unknown state.For example, when the measurement result of Cindy isand the measurement result of Alice is,the state of particleB2will turn intoa1|1〉−a2|0〉 Bob can recover the original unknown state by performingXZunitary operation on particleB2.

In this case, the unknown channel parameters cannot be eliminated and Bob cannot recover the original qubit state|γ〉t.Then Alice performs oneHgate operation on particletand one CNOT gate operation on particlestandA1.The state ofwill transform into

Although the teleportation fails in this case,according to Eq.(10),we can know that the unknown state|γ〉tis still preserved in qubitt.Hence, the integrity of the unknown state|γ〉tcan be maintained.In this way,the next teleportation can restart.

In this subsection, we present a basic two-hop nondestructive teleportation scheme based on two Bell pairs where the coefficients of quantum channel are unknown to all communication participants.In this scheme,with some simple and feasible operations, the unknown channel parameters can be eliminated probabilistically.Then the teleportation can succeed in being independent of the parameters of the Bell pairs.Even if this teleportation fails, the unknown state can still be preserved by the sender Alice, which could be retransmitted in the next teleportation.Therefore, our scheme ensures the security of communication.

2.2.Construction of direct Bell channel in chain composed of Bell pairs

Considering that the above scheme may be generalized to multi-hop nondestructive teleportation based on Bell pairs where the coefficients of quantum channel are unknown to all the communication nodes.In a multi-hop quantum chain,n(n≥2) Bell pairs are shared among the source node Alice,n−1 intermediate nodes Cindy1,Cindy2,...,Cindyn−1, and the destination node Bob.

As shown in Fig.3, Alice possesses particlestandA1.Bob owns particleBn.Cindyihas particlesBiandAi+1,i=1,2,...,n−1.The whole quantum channel can be given by

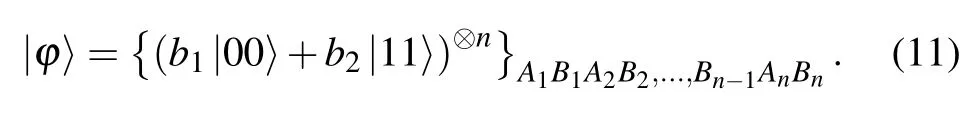
Like the above two-hop nondestructive teleportation,each intermediate node Cindyiperforms Bell one measurement on their own two particlesBiandAi+1and informs Bob of the measurement outcome(i=1,2,...,n−1).After all the Bell measurements are performed, Alice and Bob will share one direct Bell channel.

Fig.3.Qubit distribution in a quantum chain composed of Bell pairs,with dotted line denoting Bell pair.

We first consider that the relation between the measurement results of all the intermediate nodes and the Bell channel.Now we label the measurement outcome of Cindyiaspi(pi= 0 denotes the outcome=1 represents the result,i= 1,2,...,n−1).The relationship between Bell measurement results ofn−1 intermediate nodes and the direct Bell channelwhich is finally shared by Alice and Bob can be expressed as follows.[32]

If the number ofpi=0 among all the intermediate nodes is odd,then

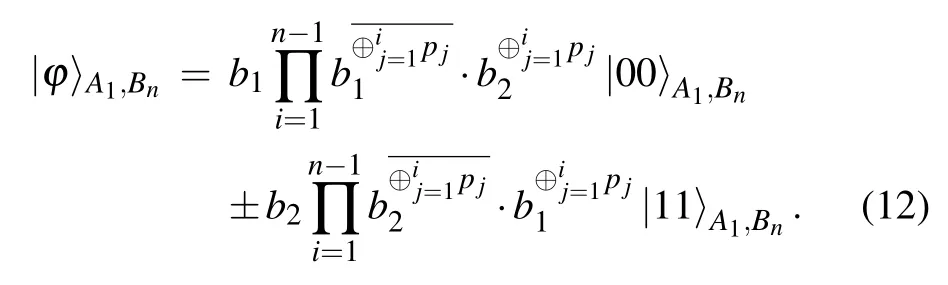
If the number ofpi=0 among all the intermediate nodes is even,then

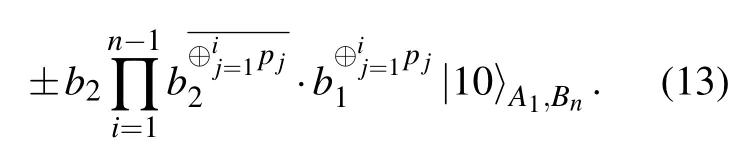
Here the normalization condition of amplitude is ignored,anddenotes the modulo 2 addition ofp1,p2,...,pi.

According to Eqs.(12), (13) and the Bell measurement results from all the intermediate nodes, Bob can obtain the direct Bell channel.Ifis the maximally entangled state, Alice can teleport an unknown state to Bob similar to two-hop nondestructive teleportation.Otherwise, Alice cannot teleport the unknown state.

3.The multi-hop nondestructive teleportation scheme

In this section, the source node Alice wishes to teleport the unknown single-qubit state |γ〉tto the destination node Bob through 2n−1 (n≥2) intermediate nodes Cindy1,Cindy2,...,Cindy2n−1as shown in Fig.4.Each intermediate node shares the Bell pairb1|00〉+b2|11〉with his neighboring nodes where the coefficientsb1andb2are unknown to all communication participants.

Fig.4.Qubit distribution of multi-hop nondestructive teleportation based on channel matching,with dotted line denoting Bell pair.

The initial quantum state of the whole system can be written as

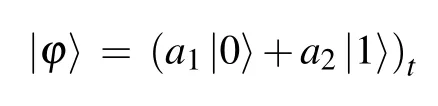
Here Alice possesses particlestandA1.Bob owns particleB2n.Cindyiowns particlesBiandAi+1,i=1,2,...,2n−1.Cindyndivides the whole quantum channel{(b1|00〉+b2|11〉)⊗2n}A1B1A2B2,...,A2nB2ninto one upstream channel{(b1|00〉+b2|11〉)⊗n}A1B1...AnBnand one downstream channel.

Our scheme can be completed in the following four steps as shown in Fig.5.

Step 1Intermediate nodes Cindy1,Cindy2,...,Cindyn−1in upstream channel, and Cindyn+1,Cindy2,...,Cindy2n−1in downstream channel respectively perform one Bell measurement on their own two particles simultaneously and send the measurement result to the node Cindyn.Then according to Eq.(12),Eq.(13),and 2n−2 measurement results from intermediate nodes,Cindyncan obtain one upstream direct channel asand one downstream direct channel as.Here |φ〉A1Bnis shared by Alice and Cindyn.is shared by Cindynand Bob.

Step 2Now the channel matching is ready to begin according to the stateand the state.For simplicity, the amplitude parameters of the stateare assumed to be ±c1and ±c2, and the amplitude parameters of the stateare assumed to be ±dand ±d2(where|c1|2+|c2|2=1 and|d1|2+|d2|2=1).

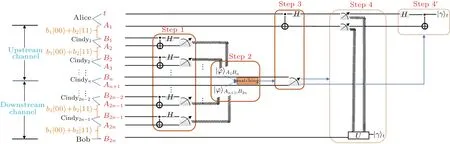
Fig.5.Quantum circuit for multi-hop nondestructive teleportation scheme based on channel matching.

If the amplitude parameters of both statesandsatisfy |c1|=|d1| or |c1|=|d2|, then the channel matching between the upstream channel and the downstream channel succeeds.For convenience, we take for example the state=c1|00〉+c2|11〉 and the state=c2|01〉+c1|10〉 to explain the matching principle.Now the entire system will become

According to Eqs.(15) and (6), we can know that the multi-hop nondestructive teleportation turns into two-hop nondestructive teleportation among Alice, Cindyn, and Bob now.In this case,Alice can teleport the unknown state to Bob.And the channel matching between upstream channel and downstream channel succeeds.Our scheme will come to Step 3.

However, when the amplitude parameters of both statesandsatisfy |c1|/=|d1| and |c1|/=|d2|, the channel matching between upstream channel and downstream channel fails.For instance,if the stateisand the stateis,then the entire system will become

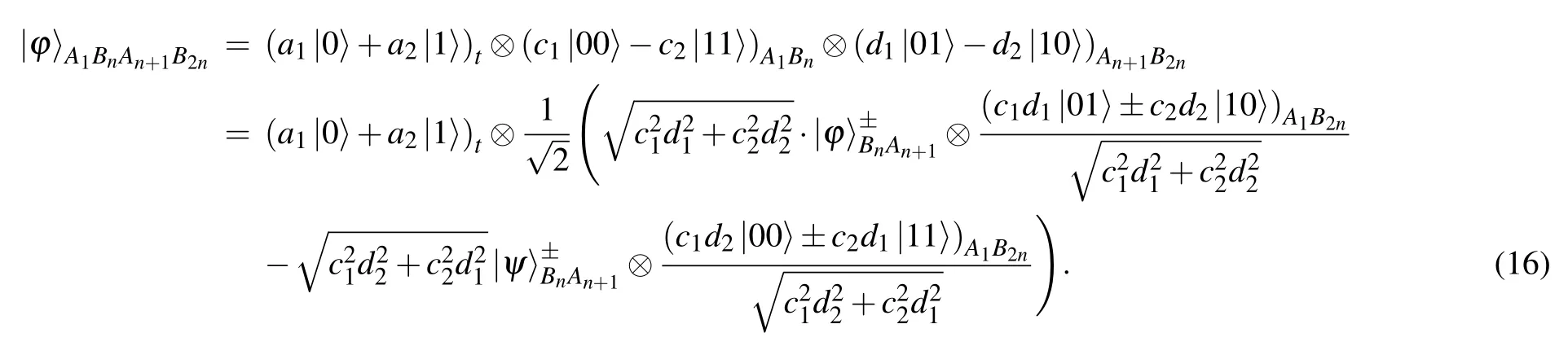
Now Cindynperforms one Bell measurement on her two particlesBiandAi+1.From Eq.(16),it is obvious that no matter what the Bell measurement result of Cindynis, Alice and Bob finally cannot share a maximally entangled state.Then this multi-hop teleportation fails.Fortunately, the unknown state is still preserved by the sender Alice.It can be teleported in the next teleportation.

Step 3The scheme to be adopted below is similar to the above two-hop nondestructive teleportation scheme.Alice performs one CNOT gate on her own particlestandA1,and then performs oneHgate on her particlet.The state|φ〉tA1BnAn+1B2nin Eq.(15)will become

Then Cindynperforms one Bell measurement on her two particlesBiandAi+1with the basis {|φ〉±=, and informs Alice and Bob of her measurement result.

Next, when the measurement outcome of Cindynis,the scheme will come to Step 4.Otherwise,it will come to Step 4′.

Step 4According to Eq.(18),if the Bell measurement result of Cindynis,the state of the remaining particlest,A1,andB2nwill become

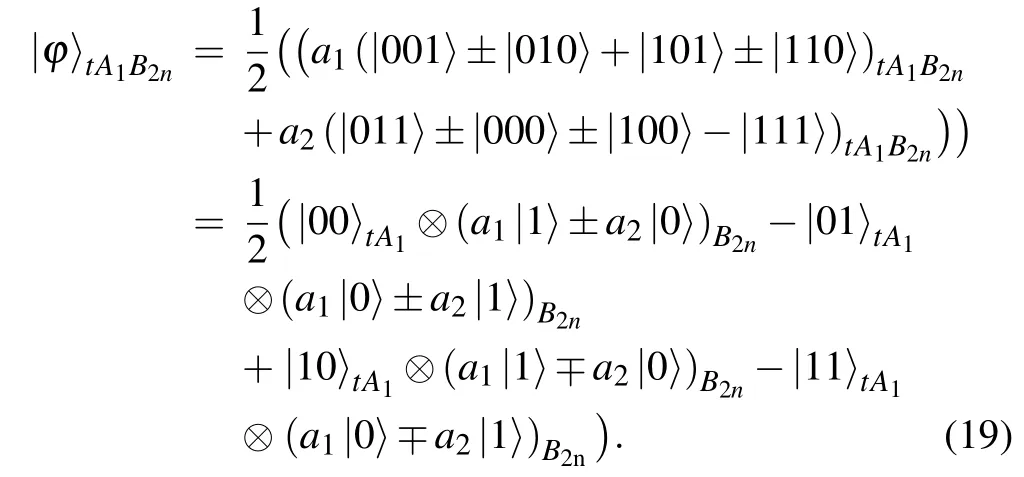
The next operations are similar to the operations in above two-hop nondestructive teleportation scheme.Alice performs one projection measurement on her two particlestandA1with the basis{|00〉,|01〉,|10〉,|11〉}and informs Bob of her measurement result.

Finally, according to Alice’s measurement result, Bob performs corresponding local unitary operation on his particleB2nto recover the unknown single-qubit state|γ〉t.

Step 4′A scheme to be used below is similar to the above two-hop nondestructive teleportation scheme as indicated in Subsection 2.1, Alice performs one extraHgate operation on her particletand then performs one CNOT gate operation on her two particlestandA1.Then the unknown qubit state|γ〉tcan be preserved on particlet.

In this section, we present a multi-hop nondestructive teleportation independent of channel parameters based on 2nBell pairs, where the coefficients of quantum channel are unknown to all the communication nodes.By using the Bell measurement, a series of local unitary operations, and channel matching technology,the source node Alice can efficiently teleport an unknown qubit state to the destination node Bob with the help of 2n−1 intermediate nodes.Even if this teleportation fails, our scheme can preserve the initial unknown state|γ〉t.It can continue to be retransmitted in the next teleportation.

4.Performance analysis

In this section,we discuss the performance of our scheme in terms of classical communication cost and quantum communication delay.Besides,we compare our scheme with some previous teleportation schemes.

4.1.Classical communication cost

The quantity of classical data that need to be transmitted can be defined as the classical communication cost in the scheme.[17]In our scheme,the classical data which need to be transmitted,are the Bell measurement data from intermediate nodes, and two-qubit projection measurement data from the source node.Both Bell measurement and two-qubit projection measurement has four possible results, which can be denoted by 2-bit classical information 00, 01, 10, 11.Then the total communication cost is the product of the bit number of each measurement result and the node number that need to transmit measurement result in the protocol.[17]Therefore,the classical communication cost in our scheme is

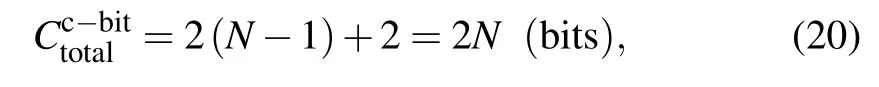
whereNis the number of hop counts in the multi-hop nondestructive teleportation scheme.

4.2.Quantum communication delay

In the quantum network, the delay introduced by measurements, unitary operations and the transmission of measurement results via classical channels is inevitable.It should be kept as low as possible due to the limited decoherence time in quantum memory and quality of service.It is assumed that each intermediate node takesDBMseconds to complete the Bell measurement and takesDtrans1seconds to transmit measurement outcome results.The source node Alice takesDPMseconds to finish the two-qubit projection measurement and takesDtrans2seconds to transmit measurement result.The unitary operations of our scheme consist of CNOT gate,Hgate,and Pauli operators(includingI,Z,X,XZoperators).The corresponding unitary operation delays can be given byDCN,DH,andDPaurespectively.

The delay of the channel matching is negligible.Thus,our scheme can be divided into three parts.The first part delayD1,includingDBM,Dtrans1,can be expressed as

The second part is that after the channel matching between upstream channel and downstream channel succeeds,Alice performs one CNOT gate on her own particlestandA1,and then performs oneHgate on her particlet.Meanwhile,Cindynneeds to perform Bell measurement on her two particlesBiandAi+1.Thus,the second part delayD2can be written as

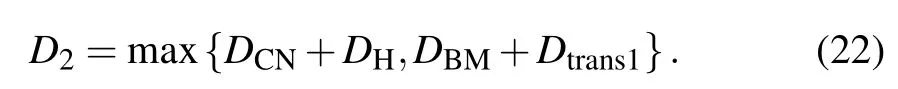
The third part is that according to the measurement outcome of Cindyn, Alice will perform projection measurement on her two particlestandA1.Next, Bob will perform corresponding local unitary operation on his particleB2nto recover the unknown single-qubit state according to Alice’s measurement result.Thus,the third part delayD3can be given by

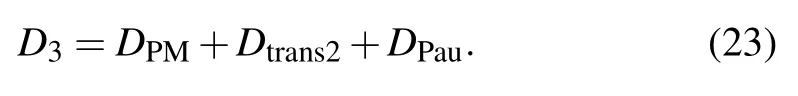
Therefore, the total delay of successful teleportation of our scheme is

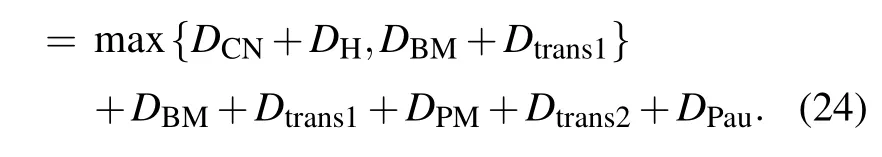
Besides,with the channel matching technology,the intermediate node Cindyncan probabilistically eliminate the unknown channel parameters according to the Bell measurement results from upstream channel and downstream channel.Then Alice and Bob can share one maximally entangled Bell channel.The teleportation can succeed in being independent of the parameters of the Bell pairs.Once this teleportation fails,the unknown state can still be preserved by Alice.The integrity of the information can be preserved.Hence,our scheme ensures the security of communication.

5.Comparison

In previous nondestructive teleportation schemes,[29,31]it is necessary to use the known quantum channels, introduce auxiliary particles and perform two-qubit unitary operations.However,in our protocol,the teleportation can succeed in being independent of the channel parameters without extra auxiliary particles or two-qubit unitary operations.Therefore, it reduces the requirements for the quantum channel itself and makes the experiment implemented more conveniently.

In addition,we also compare the efficiency of our protocol with those of previous multi-hop teleportation schemes in two aspects: communication cost and communication delay,as demonstrated in Table 1.Owing to the channel matching technology and extra one Bell measurement performed by the intermediate node,the communication delay of our scheme is higher than those of the protocols in Refs.[10,21].However,with the simultaneous entanglement swapping technology in both the upstream channel and downstream channel, the total communication delay of our scheme is lower than those in Refs.[10,24].

Table 1.Comparisons of efficiency among previous QT protocols. N is the number of hop counts in the quantum network.

6.Conclusions

In this paper,we present a multi-hop nondestructive teleportation scheme based on the Bell pairs, where the coefficients of quantum channel are unknown to all the communication nodes.With basic Bell measurement,single-qubit unitary operations and channel matching technology,it is possible for the sender and the receiver to share one maximally entangled Bell channel.Then the teleportation can succeed in being independent of the parameters of the Bell pairs.Our scheme preserves the initial unknown state even if the teleportation fails.Thus,it ensures the security of communication.Besides,our scheme firstly generalizes the teleportation to the scenario independent of channel parameters and auxiliary particles and multi-qubit unitary operations are avoided,which reduces the quantum channel requirement and enhances the flexibility of implementation.

Acknowledgements

Project supported by the Tang Scholar Project of Soochow University, the National Natural Science Foundation of China(Grant No.61873162),and the Funds from the Jiangsu Engineering Research Center of Novel Optical Fiber Technology and Communication Network and Suzhou Key Laboratory of Advanced Optical Communication Network Technology.