岔管引水系统对低频振荡的影响

郭 庆

（山东泰山抽水蓄能电站有限责任公司，山东 泰安 271000）

1 引言

水力发电系统是一个集水机电于一体的耦合系统，水力发电机组的稳定运行直接关系着电网的安全可靠运行[1]。压力引水式水电站多采用一管多机水力系统布局，其水力耦合的影响已有研究，但水力模型为刚性水击模型，在研究小干扰稳定问题时缺乏精确表达。党杰 等[2]基于单机无穷大系统，利用阻尼转矩分析法和特征值分析法研究了储能装置抑制系统低频振荡的作用机理。高慧敏 等[3]基于模态级数法研究水电站二阶振荡模式及非线性指标，考虑了水力耦合和非线性特性相互作用对系统振荡模式的影响。YANG 等[4]对水电站水力阻尼进行定量研究，分析了其对电力系统低频振荡的影响。粟欢[5]采用特征值分析方法对电网小干扰稳定性进行了分析，有效抑制了低频振荡的发生，但没有研究水力参数对低频振荡的影响。此外，尾水管压力脉动对低频振荡影响也很大[6]。

低频振荡问题是严重危害水电机组安全稳定运行的重要问题之一，国内水电机组都曾多次出现此事故，专家们针对性分析机组发生低频振荡的原因，提供相应建议措施，从而抑制低频振荡的发生[7-9]。但与研究水力机组小干扰稳定相比，更多学者则是偏重机组的稳定暂态问题[10]，甚至有学者通过复杂水力系统的解耦进行稳定性分析和控制策略的研究[11]。另外，对于多机组电站，为减少主变压器台数，通常采用扩大单元接线方式，增加的电气联系加强了机组间的耦合问题，文献[12]详细地研究了扩大单元接线对低频振荡的影响。

文中以简单的一管双机扩大单元接线机组为研究对象，水力系统采用适合于小干扰稳定分析的二阶弹性水击模型，建立水机电整体数学模型。采用特征分析法[13]及灵敏度方法[14，15]，对是否考虑水力耦合和不同引水系统布局下机电振荡模式阻尼及相应参数灵敏度进行了分析研究，明确了岔管引水系统在低频振荡中的作用，为分析复杂水力系统对低频振荡的影响提供了理论依据。

2 数学模型

2.1 水轮机及调速器数学模型

小波动时，混流式水轮机数学模型[16]为：

式中：mt、q、y、x和h分别为力矩、流量、导叶开度、转速和水头偏差的相对值（均取标幺值）；ey、ex和eh分别为水轮机力矩对导叶开度、转速和水头的传递系数；eqy、eqx和eqh分别为水轮机流量对导叶开度、转速和水头的传递系数。

采用具有测频微分缓冲型PID调速系统结构，小干扰时忽略调速器限幅作用及接力器死区，其框图如图1所示。

图1 调速系统框图

图1 中：Kn为测频微分回路增益；Tn为测频微分回路时间常数（s）；Ty1为中间接力器时间常数（s）；Ty为主接力器时间常数（s）；Td为微分时间常数（s）；bt为暂态转差系数；bp为永态转差系数。

2.2 水力系统数学模型

图2为具有公共引水管道的双机水力系统示意图，已知各管道水流惯性时间常数Tw和水击相长Tr，且管路特性系数hw=Tw/Tr。

图2 一管双机水力系统示意图

不考虑水力摩阻损失，并计及机组间的水力耦合，岔管引水系统的弹性水击模型如图3所示。其中，hwi和Tri分别为与相应管道对应的管路特性系数和水击相长，下标0、1T、2T、1B、2B的含义同图2。Qt1（s）、Ht1（s）、Qt2（s）、Ht2（s）分别表示1号机和2号机流量和水头的拉氏变换。将方框中的传递函数进行泰勒级数展开，并且分子取一项、分母取两项，对每个框图中传递函数分别进行状态方程的转换并消去多余状态变量，便得到系统的状态空间描述方程。

2.3 扩大单元接线数学模型

图4所示为双机扩大单元接线，经变压器和输电线路连接到无穷大母线系统的等值电路图。忽略机组间连接阻抗，Ut为机端电压，U0为无穷大母线电压（参考电压），Z为变压器和输电线等效阻抗。

图3 岔管引水系统弹性水击模型

图4 机网接口示意图

采用多机Heffron-Philips模型[17]，该模型由常规Heffron-Philips模型拓展得到，并可处理发电机间不经阻抗直接相联的情况。在分析小干扰稳定问题时，模型得到了广泛的应用。扩大单元接线的发电机模型如图5所示。其中，K2~K6为发电机模型系数矩阵；采用快速励磁系统，KA为励磁系统增益，TE为励磁系统时间常数（s），T′d0为发电机时间常数（s），D为发电机阻尼系数，以上均为对角矩阵。

图5 发电机Heffron-Philips模型

2.4 一管双机系统水机电整体状态方程

综合上述各部分数学模型，采用状态方程-特征根分析法得到系统的整体状态方程：

其中，X为系统状态变量，A为系数矩阵。

3 水力耦合对低频振荡阻尼的影响

考虑两台机组均在额定工况下运行，建立系统的状态方程，基于特征分析法得到系统的所有振荡模式，采用参与矩阵和灵敏度方法进行分析，通过划分系统的振荡模式，得到相应的振荡模式阻尼及其对参数变化的灵敏度。图6和图7分别为是否考虑水力耦合时机电振荡模式阻尼随公共管道参数和变化的散点图。

图6 机电振荡模式阻尼随Tr变化的散点图

图7 机电振荡模式阻尼随hw变化的散点图

这里，由于两台机组各参数及运行工况相同，计算得到的两个机电振荡模式与两台机组的Δω、Δδ强相关性也相同。图6和图7表明：水力耦合对机电振荡模式阻尼的影响较小，主要体现在对机电振荡模式2的影响上，且考虑水力耦合时总的机电振荡模式阻尼略小，因此当计算小干扰稳定性时，不宜将岔管引水系统简化为不考虑水力耦合的单机单管系统进行分析；参数Tr和hw对机电振荡模式阻尼的影响同样很小，无论是否考虑水力耦合，机电振荡模式的阻尼变化都比较小；但是随着Tr的增加，总的阻尼也会增加，说明增加管道的长度有利于抑制低频振荡，此时水力耦合对机电振荡模式阻尼的影响在减小；而随着hw的增加，总的阻尼会减小，此时水力耦合对机电振荡模式阻尼的影响略有增加。

对同时考虑扩大单元接线的机组，一台发电机增加阻尼会对另一台发电机的机电振荡模式产生影响，但水力耦合对这种影响的作用尚未详细研究过。对于文献[12]提出的考虑扩大单元接线时，双机增加较小阻尼和单机增加较大阻尼对低频振荡的抑制效果相同，文中计算过程中已做验证。因此，本文将主要研究低频振荡模式对其中一台发电机阻尼的灵敏度（以1号机阻尼D1为例），并对水力耦合的影响进行分析。

图8和图9分别为机电振荡模式阻尼对D1的灵敏度（实部）随公共引水管道参数Tr和hw变化的散点图。如图8、图9所示，由于机组阻尼的分配，每台机组出现了对应的强相关机电振荡模式。图示曲线表明：考虑水力耦合，2号机强相关机电振荡模式对参数D1的灵敏度明显变小，说明水力耦合会减弱1号机增加阻尼抑制2号机低频振荡的作用，但由于灵敏度变化的数量级很小，因而水力耦合的影响是很小的；与参数Tr和hw对机电振荡模式阻尼的影响情况类似，当Tr较小或者hw较大时，水力耦合对上述灵敏度的影响略大。

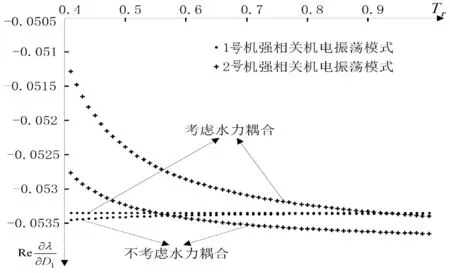
图8 机电振荡模式阻尼对D1的灵敏度（实部）随Tr变化的散点图

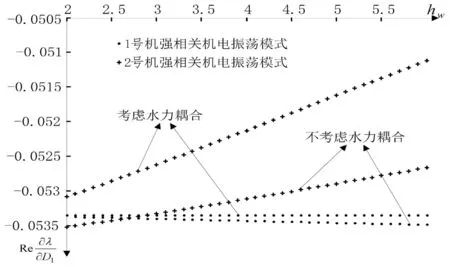
图9 机电振荡模式阻尼对D1的灵敏度（实部）随hw变化的散点图

综上可知，水力耦合对低频振荡的影响很小，但当研究小干扰稳定问题时，是不能为了简化水力系统而忽略水力耦合影响的；当Tr较小或者hw较大时，水力耦合对低频振荡的影响略大，反之则越小。

4 岔管与单机单管对低频振荡影响的比较

对于多机组具有压力引水管道的水电站，采用分岔管道水力系统布局和单管单机水力系统布局对低频振荡的影响还没有详细研究过。单管单机的水力系统平面图如图10所示，采用传统的二阶弹性水击模型，模型的处理与前述相同。为作比较，除公共引水管道发生变化外，其余参数及机网接口均与一管双机系统相同。

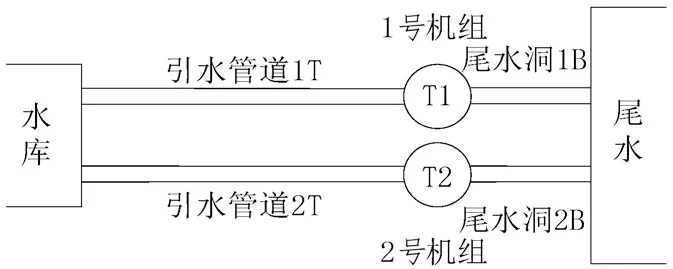
图10 单机单管水力系统平面图

图11 为岔管引水系统和单机单管引水系统下的机电振荡模式阻尼随压力引水管道参数Tr变化的散点图。可见，对岔管引水系统，随着Tr的增加，系统的机电振荡模式阻尼略有增加，但增加幅度很小，而单机单管引水系统下的机电振荡模式阻尼却受Tr影响很大，在一定范围内，随着Tr的增加机电振荡模式总的阻尼先增加后减小，而Tr主要由管道长度决定，这也说明当其他参数固定时，引水管道较短时单管单机引水系统布局有利于低频振荡模式阻尼，管道较长时岔管引水系统布局对低频振荡模式更为有利，并且通过变化的趋势可以看出，当管道较长时，单机单管引水系统反而容易造成低频振荡。

图11 机电振荡模式随Tr变化的散点图

图12 为单机单管引水系统压力管道特性系数变化时系统机电振荡模式阻尼的散点图。此时，相当于两机组仅有电气联系而没有任何水力联系，与忽略水力耦合的情况相比，该水力系统管道特性系数hw也发生了变化，因此对于参数hw不再具有可比性。其他参数不变时，随着hw的增加，一种机电振荡模式阻尼略有减小，另一种机电振荡模式阻尼却明显增加，并且由负阻尼转变为正阻尼，但当到达一定值后开始减小，因而总的阻尼会在某个值达到最大，这说明：对应于尾水管道的某个hw值，压力引水管道总有较为合适的hw值与之对应。

图12 机电振荡模式随hw变化的散点图

图13 为分别采用岔管引水系统和单管单机引水系统时机电振荡模式阻尼对D1的灵敏度（实部）随参数Tr变化的散点图。图13表明，采用岔管引水系统时，1号机强相关机电振荡模式的阻尼与2号机强相关机电振荡模式的阻尼对D1的灵敏度基本一样，结合图8可知，随着Tr的增加，1号机强相关机电振荡模式的阻尼对D1的灵敏度先高于2号机后略低于2号机；采用单机单管引水系统时，1号机强相关机电振荡模式的阻尼与2号机强相关机电振荡模式的阻尼对D1的灵敏度明显不同，并且随着Tr的增加，2号机强相关机电振荡模式的阻尼对D1的灵敏度高于1号机并逐渐增加到一个最大值，然后开始减小直至低于1号机。

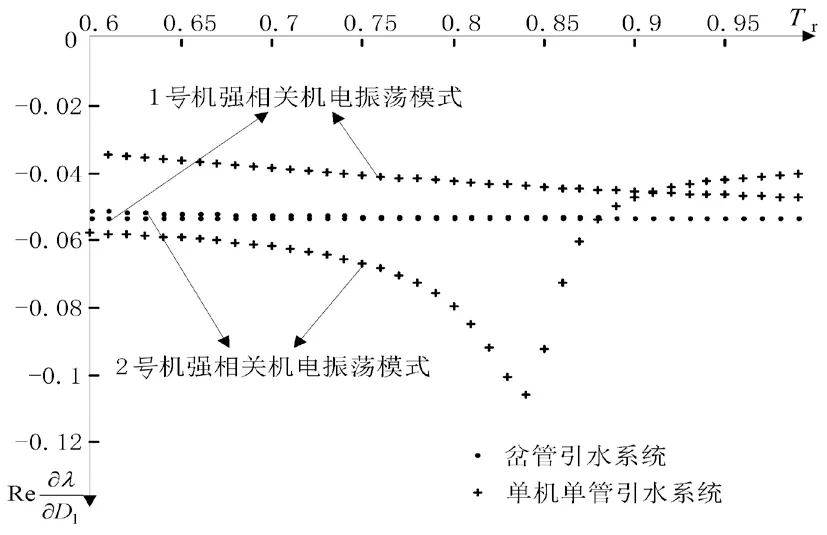
图13 机电振荡模式阻尼对D1的灵敏度（实部）随Tr变化的散点图

图14 为采用单管单机引水系统时机电振荡模式阻尼对D1的灵敏度（实部）随hw变化的散点图。可见，当hw较小时，1号机强相关机电振荡模式的阻尼对D1的灵敏度高于2号机，但随着hw的增加，2号机强相关机电振荡模式的阻尼对D1的灵敏度开始增加并达到一个最大值，然后随着hw的继续增加开始减小，直至低于1号机，与图12相比可知，机电振荡模式总阻尼最大时的hw值与2号机强相关机电振荡模式的阻尼对D1最大灵敏度的hw值相同，这也说明，选择合适的压力引水管道hw值不仅有利于机组低频振荡阻尼，而且对机组增加阻尼抑制低频振荡的效果也最佳。

图14 机电振荡模式阻尼对D1的灵敏度（实部）随hw变化的散点图

5 结论

文中水力系统采用二阶弹性水击模型，考虑具有电气联系的机组扩大单元接线，建立了一管双机水机电整体小干扰稳定分析模型。通过对水击相长Tr和管道特性系数hw变化时系统机电振荡模式阻尼及相应灵敏度分析，明确了岔管引水系统对低频振荡的影响：

（1）岔管引水系统水力耦合对低频振荡的影响很小，但不考虑水力耦合时系统总的机电振荡模式阻尼会略大，因而当机电振荡模式阻尼较小时不宜将水力模型简化分析，以免造成理论与实际的偏差。此外，在一定范围内，当Tr较小或者hw较大时，水力耦合对低频振荡的影响略大，反之则略小。

（2）对采用压力引水管道的多机组水电站，不同的引水系统布局对低频振荡的影响很大。岔管引水系统无论是从对自身机电振荡模式阻尼方面还是对增加发电机阻尼抑制低频振荡方面受Tr和hw的影响都较小，而单机单管水力系统的低频振荡模式则受Tr和hw的影响很大。采用岔管引水系统时，增加一台机组的发电机阻尼对抑制两台机组低频振荡的效果基本相同，并且对自身的效果略好，而采用单机单管引水系统时，这种现象受参数Tr和hw的影响较大，一定范围内，增加一台机组发电机阻尼反而对抑制另一台机组低频振荡的效果明显更好。总的来看，当Tr较小时，采用单机单管引水系统对机组的小干扰稳定更为有利，反之，采用岔管引水系统更好。