基于粒子群算法的强迫风冷散热器多目标优化

王 玲 李 俐 朱翔鸥 王守冬 孙 创

基于粒子群算法的强迫风冷散热器多目标优化

王 玲1李 俐2朱翔鸥1王守冬1孙 创1

（1. 温州大学电气与电子工程学院，浙江 温州 325035； 2. 浙江正泰电器股份有限公司，浙江 温州 325603）

电力电子系统对强迫风冷散热器提出了低热阻、小型化和轻量化的要求，本文在考虑现有散热器设计方法的不足之后，通过散热器结构及其等效热阻网络构建热阻、压降和质量最小的多目标优化模型。针对当前粒子群算法求解多目标模型时存在的局限性，本文采用多种改进策略提高算法的性能。计算和仿真结果显示，优化后的强迫风冷散热器的热阻、压降、质量均有减小，功率器件表面温度明显降低，验证了多目标优化模型及算法的有效性。

强迫风冷散热器；多目标优化；粒子群算法（PSO）；改进策略

0 引言

电力电子装置向高精度、高功率密度、高可靠性方向发展的同时，功率器件的热失效和热退化现象也更为突出，更有效的散热技术成为了研究的重点。强迫风冷散热器有散热效果好、结构简单、工作稳定、成本较低等优点，因而能够广泛应用在大功率电力电子装置的热设计中，电力电子装置也对强迫风冷散热系统提出了低热阻、小型化、轻量化的要求[1]。

传统的强迫风冷散热器设计一般采用控制变量法或者试验法。文献[2]利用控制变量法分别分析了基板厚度、翅片数目及翅片厚度对散热器热阻的影响，但并未给出散热器结构参数的优化方法。文献[3]提出一种强迫风冷散热系统体积最优的设计方法，虽然结果显示散热系统的体积较传统设计降低了约30%，但散热系统的热阻和压降并未得到优化。文献[4]采用正交试验法分别探究了翅片间距、翅片高度和翅片厚度对芯片结温和散热器质量的影响，但实验法研发周期较长、成本较高。文献[5]将散热器的散热性能、体积、压降作为优化目标，通过线性加权的方法建立了优化模型，但加权方法的缺点是各个优化目标的权重值不易确定。综上所述，在以散热器散热效果为设计目标的同时，还应将散热器的压降、质量和体积等指标纳入综合设计范畴。影响散热器各指标的变量很多，如散热器的基本尺寸、翅片数量、翅片高度、翅片厚度、风速等，因此散热器的优化属于多变量多目标优化[6]。

本文在上述研究的基础上建立强迫风冷散热器的多目标优化模型，采用改进的多目标粒子群算法（particle swarm optimization, PSO）完成对散热器的结构参数在解空间内的全局寻优，获得包含提升散热性能、降低系统压降、减小系统质量在内的三目标综合优化最优解。最后，以优化后的散热器结构参数为算例来验证本文所提模型和优化方法的有效性和实用性。

1 强迫风冷散热器多目标优化模型

1.1 强迫风冷散热器热阻计算方法

图1为常见的强迫风冷散热器结构示意图。功率器件产生的热量主要通过两个传输途径散发至周围环境，一部分热量通过散热器的基板、翅片散发，另一部分热量通过芯片外壳散发。一般来说，通过芯片外壳散发的热量可忽略不计。

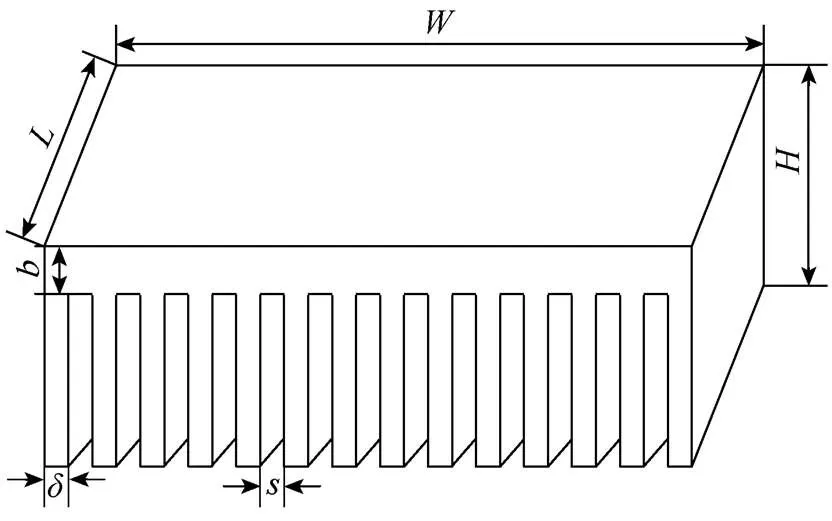
图1 强迫风冷散热器结构示意图

根据强迫风冷散热系统中热流传递路径可知，散热系统总热阻主要包括器件的结-壳热阻、壳与散热器之间的热阻及散热器与环境之间的热阻。图2为强迫风冷散热器的等效热阻网络示意图[7-9]。

图2 强迫风冷散热器等效热阻网络示意图

强迫风冷散热系统的热传递遵循热路欧姆定律，即

散热器基板传导热阻、翅片传导热阻和翅片对流热阻可以表示为

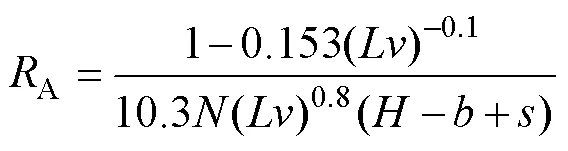
1.2 压降计算方法

传统方法通过增大散热器的外表面积来减小散热器热阻，但散热器的压降（压力损失）和质量同时也会增大。压降增大则会降低散热器的表面传热系数，使散热器性能降低，同时也需要系统更换更大风压的风扇，从而导致系统整体质量变大。因此，在保证强迫风冷散热系统热阻减小的情况下，应尽量降低或保持系统的压降。散热系统压降计算公式为[11]

1.3 强迫风冷散热系统优化模型

由式（6）可得散热器压降优化模型为

由图1可得散热器质量优化模型为

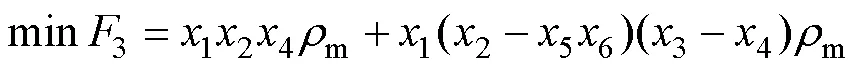
1.4 约束条件

为了保证优化后的散热器能够顺利安装在原有安装柜上，要求优化后的散热器尺寸不超过原有设计尺寸，即以优化前散热器的长度、宽度、高度为设计上限。对于功率较大的强迫风冷散热器，要求平均冷却风速不低于3m/s。散热器翅片间距不能小于1mm，否则将影响冷却空气的正常流动。为了防止散热器翅片变形，翅片厚度不能小于1mm。综上所述，散热器的参数约束条件为

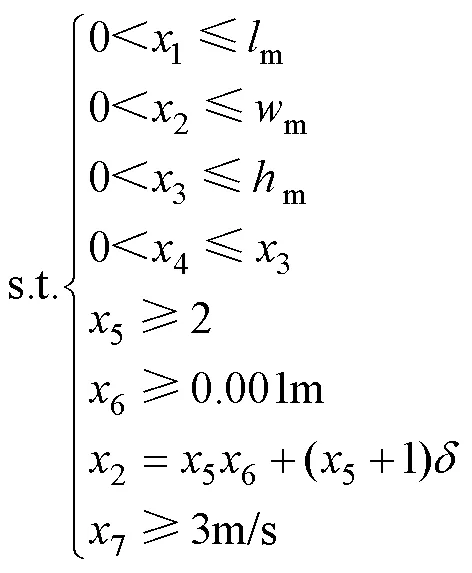
2 改进多目标粒子群算法

2.1 多目标粒子群算法

1995年Kennedy和Eberhart在一次国际学术会议上正式提出了粒子群优化算法（PSO），其基本思想是设计一种无质量的粒子来模拟鸟群，通过鸟群个体之间的协作和信息共享来寻找最优解，每个粒子可视为待优化问题的一个候选解[12]。粒子的两个属性分别是速度和位置，速度反映粒子运动的快慢，位置代表粒子运动的方向。粒子通过追踪迭代过程中的自身历史最优位置和全局最优位置进行搜索，粒子根据式（11）和式（12）更新自身的速度和位置。

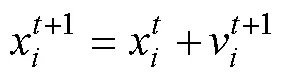
鉴于PSO简单通用、鲁棒性强、效率高、收敛快的优点，研究者尝试将PSO应用至多目标优化领域，并产生了经典的多目标粒子群优化算法（multi- objective particle swarm optimization, MOPSO）[13]。但经典多目标粒子群算法在求解散热器模型时仍存在以下问题：

1）最优解的更新和维护策略不够完善，以致最优解的多样性和分布性较差。

2）参数的取值不够灵活，算法搜索速度较慢，搜索结果过于集中。

3）对于边界的粒子处理不够灵活，以致算法局部寻优能力较差。

基于以上原因，本文使用改进后的粒子群算法对散热器多目标优化模型进行求解。

2.2 基于拥挤距离的外部档案更新策略

多目标粒子群算法会将搜索过程中获取的全局最优解存于外部档案中，从而引导算法的进化和收敛。外部档案容量的大小NP是事先确定的，当外部档案内的最优解数量达到容量限值NP时，必须对外部档案进行维护，在保证最优解多样性的基础上去除多余粒子。本文采用基于改进拥挤距离排序的外部档案更新策略[14]，具体方法如下：

1）将外部档案中所有粒子分别代入不同的目标函数中，根据不同目标函数值大小对所有粒子进行排序。

2）根据排序获取粒子在每一个目标函数空间上函数值最近的两个粒子。

3）根据式（13）计算每个粒子的拥挤距离，并根据拥挤距离大小对粒子排序。

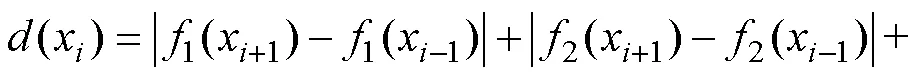
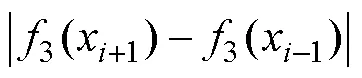
4）根据排序去除拥挤距离最小的粒子，当粒子有两个或多个时，随机选择一个去除。

5）对剩余粒子按照步骤1）～步骤4）重新计算拥挤距离，直至外部档案中最优解数量等于外部档案预设容量。

2.3 动态参数更新策略

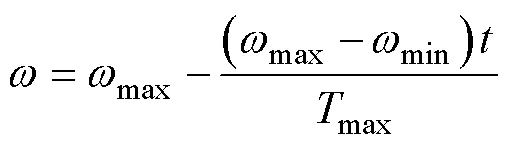
2.4 改进的边界处理方法

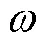
2.5 算法流程

基于改进粒子群算法的强迫风冷散热器结构参数多目标优化流程如下：

1）初始化粒子群的速度和位置，设置参数。

2）设置初始粒子种群中粒子的当前位置为粒子个体最优位置。

3）计算粒子种群中每个粒子的目标函数值，将粒子群中的非支配解更新到外部档案。

4）更新粒子自身最优位置，根据拥挤距离选取粒子种群的全局最优位置。

5）更新粒子的位置和速度。

6）计算更新后粒子目标函数值，将粒子群中的非支配解更新到外部档案。

7）判断算法是否达到最大迭代次数，若判断结果为是，从外部档案集中随机选取一个解作为散热器优化设计方案；若判断结果为否，则返回步骤4）。

3 算例与结果分析

3.1 算例分析

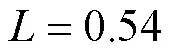
表1 改进多目标粒子群算法参数约束条件

从多目标粒子群算法优化后的最优集中随机选取3个最优解，根据式（7）～式（9）计算出散热器原方案及优化方案的热阻、压降和质量，具体结果见表2。

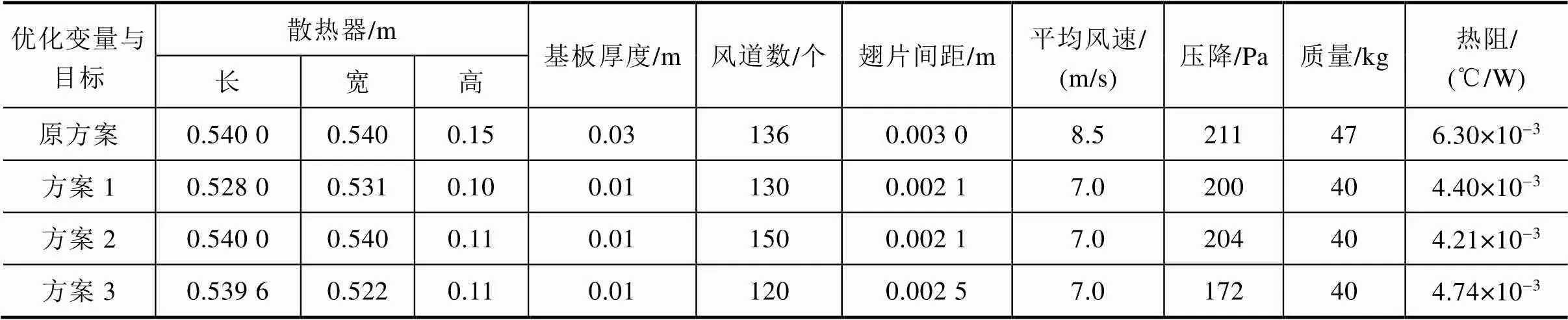
表2 散热器多目标优化前后性能对比

由表2可知，经改进多目标粒子群优化后的散热器，其热阻、压降和质量相对原方案均有减小。以方案3为例，优化后的散热器热阻相对原方案减小约24.76%、压降减少约18.48%、质量减少约14.89%，体积和质量的减少意味着使用更少的散热器制造材料，进一步节省了成本。以上结果表明，采用多目标粒子群算法对散热器进行优化设计是有效且可行的。

3.2 仿真分析

为进一步验证本文所提散热器优化方法的合理性和准确性，使用Icepak软件对优化前后的散热器进行热仿真分析。采用表2优化方案3所示参数进行散热器温度仿真，对散热系统施加相同功耗的IGBT模块（IGBT模块功率损耗为1 000W，最高允许结温为125℃）作为热源，环境温度设为40℃，IGBT模块在散热器优化前、后表面温度分布分别如图3、图4所示。由图3、图4可知，优化前IGBT模块热仿真最高温度为71.85℃，优化后IGBT模块热仿真最高温度为65.49℃，两种方案均满足系统要求，但散热系统优化后的IGBT模块最高温度相比优化前最高温度降低了6.36℃，表明了本文所提散热器优化模型和优化方法的有效性和实用性。

图3 散热器优化前IGBT模块的温度仿真

图4 散热器优化后IGBT模块的温度仿真

4 结论

本文根据散热器等效热阻网络，推导建立了热阻、压降和质量最小的多目标优化模型，拟定了合理的优化变量，并设计了相应的约束条件。针对经典多目标粒子群算法的缺陷，本文引入了多种改进策略提高了算法的搜索能力，首先算法采用改进拥挤距离的外部档案更新策略，保证了最优解集的多样性，同时也使用了动态的参数调整策略、改进的边界处理方法，使算法拥有了较强的全局搜索和局部搜索能力。通过改进的多目标粒子群算法求解散热器优化模型最优解集，采用优化后的散热器结构参数进行热仿真分析，仿真结果验证了本文所提散热器优化方法的有效性和实用性。

[1] 李广义, 张俊洪, 高键鑫. 大功率电力电子器件散热研究综述[J]. 兵器装备工程学报, 2020, 41(11): 8-14.

[2] 赵红璐, 朱永元, 张银. 大功率逆变器散热设计[J]. 电气技术, 2018, 19(8): 149-156.

[3] 林弘毅, 伍梁, 郭潇, 等. 高功率密度SiC静止无功补偿器强迫风冷散热综合建模及优化设计方法[J]. 电工技术学报, 2021, 36(16): 3446-3456.

[4] 张建新, 牛萍娟, 武志刚, 等. 大功率LED散热器性能的双目标优化[J]. 电工技术学报, 2014, 29(4): 136-141, 165.

[5] 李劲松, 杨庆新, 牛萍娟, 等. 基于遗传算法及MATLAB仿真的大功率LED散热器优化设计与分析(英文)[J]. 电工技术学报, 2013, 28(增刊2): 213-220.

[6] 施渺, 杜江伟, 余小玲, 等. 平直翅片热管散热器的正交数值模拟优化[J]. 电子机械工程, 2020, 36(2): 14-18.

[7] 张健. 电力电子器件及其装置的散热结构优化研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.

[8] 姜鑫, 应展烽, 万萌, 等. 计及环境对流随机性的功率器件结-环境热网络模型[J]. 电工技术学报, 2021, 36(14): 3090-3100.

[9] 任磊, 沈茜, 龚春英. 电力电子电路中功率晶体管结温在线测量技术研究现状[J]. 电工技术学报, 2018, 33(8): 1750-1761.

[10] 周涛, 陆晓东, 李媛. 功率半导体器件风冷散热器热阻计算[J]. 渤海大学学报(自然科学版), 2011, 32(3): 228-235.

[11] 梁帅奇, 张华润, 姜辉, 等. 某型强制风冷直流变压器机柜风道设计与优化[J]. 电力电子技术, 2021, 55(2): 50-53.

[12] EBERHART R, KENNEDY J. A new optimizer using particle swarm theory[C]//MHS95 Sixth International Symposium on Micro Machine & Human Science, Nagoya, Japan, 2002.

[13] COELLO C, PULIDO G T, LECHUGAM S. Handling multiple objectives with particle swarm optimi- zation[J]. IEEE Transactions on Evolutionary Com- putation, 2004, 8(3): 256-279.

[14] 廖宗毅, 万文略. 基于改进多目标差分进化算法的安全约束动态环境经济调度[J]. 电气技术, 2020, 21(8): 22-27.

[15] 田峰, 林荣文, 武迪. 基于改进粒子群算法的伺服系统多参数整定研究[J]. 电气技术, 2019, 20(9): 26-30.

[16] 王东风, 孟丽, 赵文杰. 基于自适应搜索中心的骨干粒子群算法[J]. 计算机学报, 2016, 39(12): 2652-2667.

Multi-objective optimization of forced air-cooled heatsink based on particle swarm optimization algorithm

WANG Ling1LI Li2ZHU Xiang’ou1WANG Shoudong1SUN Chuang1

(1. School of Electrical and Electronic Engineering, Wenzhou University, Wenzhou, Zhejiang 325035; 2. Zhejiang Chint Electrics Co., Ltd, Wenzhou, Zhejiang 325603)

The power electronic system requires forced air-cooled heatsink which has low thermal resistance, miniaturization and lightweight. In this paper, a multi-objective optimization model with minimum thermal resistance, pressure drop and mass is established based on the radiator structure and its equivalent thermal resistance network after considering the shortcomings of existing radiator design methods. In view of the limitations of the current particle swarm algorithm when solving multi-objective models, this paper adopts a variety of improved strategies to improve the performance of the algorithm. The calculation and simulation results show that the thermal resistance, pressure drop, and mass of the optimized forced air-cooled radiator are all reduced, and the surface temperature of the power device is significantly reduced, which verifies the effectiveness of the multi-objective optimization model and algorithm.

forced air-cooled heatsink; multi-objective optimization; particle swarm optimization (PSO); improved strategy

2021-09-01

2021-09-14

王 玲（1995—），男，重庆巫山县人，硕士研究生，研究方向为电机与电器。