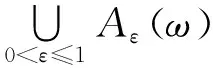加法噪声驱动的随机Lorenz系统吸引子及其上半连续性
2022-02-24刘桂芬赵文强
刘桂芬, 赵文强
(重庆工商大学 数学与统计学院,重庆 400067)
0 引 言
Lorenz系统是由两无限平板间热对流模型推导出的大气流体动力学模型[1],其被广泛研究[2-3]。Lorenz吸引子是确定性混沌的一个例子,Stewart[4]首次通过严密的推论证明了非随机情形吸引子的存在,在此之前只能通过计算机数值模拟近似产生,随后全局吸引子的存在性由Robinson[5]和Temam[6]获得。Robinson通过建立中心在z轴上足够大的球体证明了非随机情形的全局吸引子的存在性,较Temam对系统参数加以限制的证明更巧妙。然而,实际大气流体受不确定性因素影响,比如海啸、地震等,非随机情形的Lorenz系统无法完全描述这些偶然因素对大气运动规律性的影响。
关于随机Lorenz系统的研究由文献[7-8]提出,文献[7]介绍了在解指数稳定的条件下,随机Lorenz Stenflo系统的全局吸引集的估计与离散分岔行为。最近,SchmallfuB[8]研究了乘法噪声下Lorenz系统吸引子的存在性和维数估计。乘法噪声仅仅增加了乘积因子,没有改变方程的结构,而在加法扰动下,方程的形式显著变化,产生了更多的扰动项,方程的结构更复杂。到目前为止,带加法白噪声的随机Lorenz系统吸引子的存在性和上半连续性问题仍然未知。
考虑如下Lorenz系统在加法噪声下的随机动力行为:
(1)
初始条件:x(0)=x0,y(0)=y0,z(0)=z0。在式(1)中,3个变量x,y,z分别表示温度、湿度和压力;σ,b,r都为正的实参数,σ表示普朗特数,r为瑞利数;dW1,dW2,dW3代表白噪声;W(t,ω)=(W1(t,ω),W2(t,ω),W3(t,ω),)为概率空间(Ω,F,P)上的双边实值Wiener过程,具体形式在后面给出;ε≥0为噪声强度。本文拟利用文献[9]定理3.1关于上半连续的结果去研究随机扰动情况下的Lorenz系统随机吸引子的存在性及上半连续性等。在对解的估计过程中,Ornstein-Uhlenbeck的遍历性具有重要作用,所得结果没有对系统的参数给以其他限制[6]。关于随机吸引子的相关理论,读者可参加文献[10-11]等。
文章的结构如下:第一部分通过变量代换把随机Lorenz方程组转换成含随机参数的确定性方程组;第二部分证明了随机Lorenz方程组吸引子的存在性;第三部分先验证了方程组解的积分具有有界性,接着通过不等式估计和Gronwall引理等,研究了当ε→0时,随机Lorenz方程组的解收敛到确定的方程的解,最后验证了随机吸引子的上半连续性。
1 随机动力系统
本文涉及的概率空间为三维Wiener概率空间(Ω,F,P),也就是说
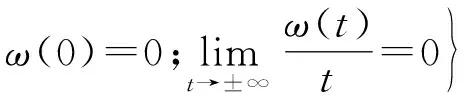
F是由Ω生成的Borelσ-代数,P是(Ω,F,P)上的Wiener测度,把三维的Wiener过程W(t,ω)和Ω中的连续函数ω(t)=(ω1(t),ω2(t),ω3(t))等同,并定义时间平移θtω(s)=ω(s+t)-ω(t),ω∈Ω,s,t∈R,可以验证(Ω,F,P,(θt)t∈R)为距离动力系统。
现在为了将连续随机动力系统与随机Lorenz方程组联系起来,需要将带有随机附加项的方程组变换转化为带有随机参数的确定性方程组。为此考虑O-U随机微分方程:
dηj+λjηjdt=dωj(t),λj>0,j=1,2,3
(2)
可以很容易得到式(2)的解为
ηj(t)=ηj(θtωj)=
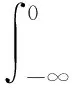
需要满足一定的条件:
用O-U过程先对Lorenz方程组式(1)作变量代换,令
x=X+εη1(θtω1)
y=Y+εη2(θtω2)
z=Z+εη3(θtω3)
则原方程组改写为
(3)
具有初始值:
X(0,0,ω,X0)=x0-εη1(ω1),Y(0,0,ω,Y0)=
y0-εη2(ω2),Z(0,0,ω,Z0)=z0-εη3(ω3)
定义集合族Δ为R3空间中满足如下指数收敛条件的随机集的全体:
(4)
其中,c0=min{σ,b,1}。
2 随机吸引子的存在性
本节讨论Lorenz系统随机吸引子的存在性。首先通过恰当的估计获得了以(0,0,r+σ)为球心的吸收集的存在性,其中r>0,σ>0没有其他限制[4]。
引理1 设集合族Δ由式(4)所定义,0<ε≤1,B={B(ω)}ω∈Ω∈Δ,则对P-a.e.ω∈Ω,{x0(θ-tω),y0(θ-tω),z0(θ-tω)}∈B(θ-tω),存在T(B,ω)>0,使得对所有的t≥T(B,ω),有x2(t,0,θ-tω,x0(θ-tω))+y2(t,0,θ-tω,y0(θ-tω))+z2(t,0,θ-tω,z0(θ-tω))≤r(ω),其中:
(b(r+σ)2+c1εM2(θsω))ds+2(r+σ)2
为有限的随机变量,这里c0,c1为确定的正常数。

证明根据方程组式(3),可得

(5)
下面对上述不等式右端的每一项给出恰当的估计。注意到假设σ,r,b>0,则运用Young不等式,式(5)中右边各项分别估计为
(6)
(7)
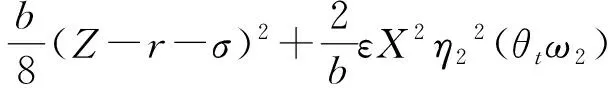
(8)
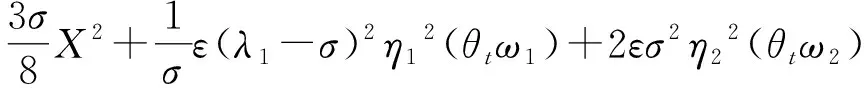
(9)
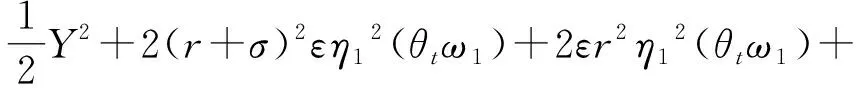
(10)
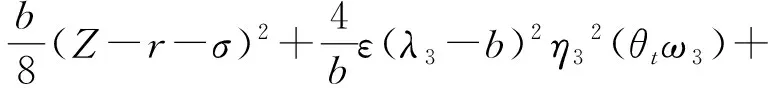
(11)
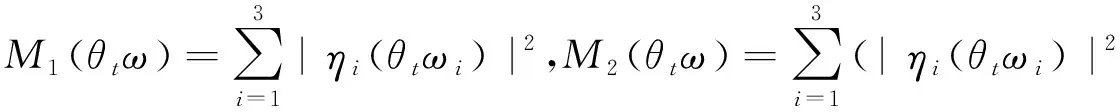
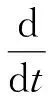
(12)
其中,c1为依赖于σ,b,r的确定的正常数。在式(12)中,运用Gronwall引理,并令s-t=s′,r-t=r′,有
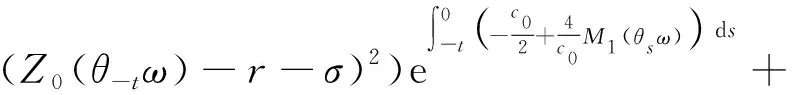
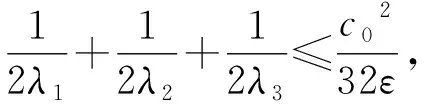
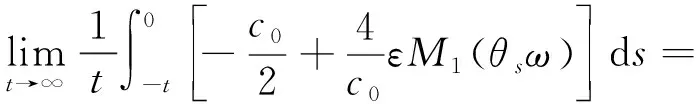
则存在充分大的T0,当t>T0时成立,有
故当t>T0时,有
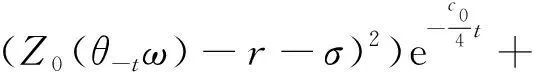
(13)
容易验证式(13)右端第二项中的积分是有限的。由变量代换x=X+εη1(θtω1),y=Y+εη2(θtω2),z=Z+εη3(θtω3),即有
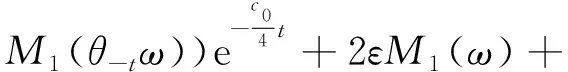
因为{x0(θ-tω),y0(θ-tω),z0(θ-tω)}∈B(θ-tω)和M1(θ-tω)关于t最多二次多项式增长,因此存在T1>T0,当所有的t>T1时,有
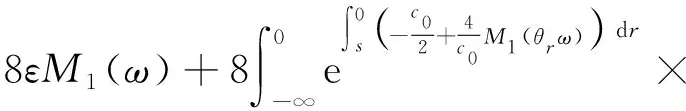
从而引理1得证。
根据方程组式(1)的解算子{x(t,0,ω,x0),y(t,0,ω,y0),z(t,0,ω,z0)}定义随机动力系统φ:φ(t,ω,(x0,y0,z0))=(x(t,0,ω,x0),y(t,0,ω,y0),z(t,0,ω,z0))。令K(ω)={(x,y,z):x2+y2+z2≤r(ω),ω∈Ω},半径r(ω)由引理1确定,则有如下存在性结果。
定理1 对任意的ε∈(0,1],由Lorenz方程组式(1)确定的随机动力系统φ存在唯一的Δ-随机吸引子{A(ω)}ω∈Ω,其中
证明由引理1, 对ω∈Ω及任意的x∈R3,有

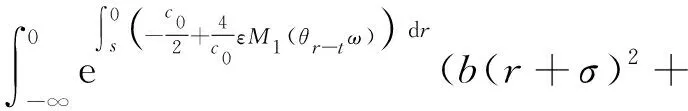
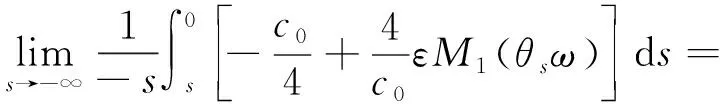
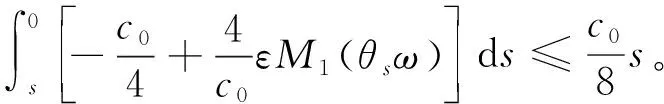
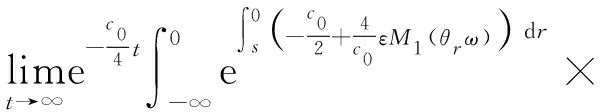
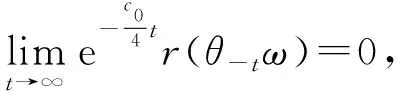
3 随机吸引子的上半连续性
为了获得随机吸引子的上半连续,需要证明随机Lorenz方程组的解关于参数ε的收敛结果,为此预先证明解的积分有限。
引理2 设ε∈(0,1],ω∈Ω,T>0,(Xε,Yε,Zε)是方程组式(3)当初值为(Xε(0),Yε(0),Zε(0))时的解,则存在常数c1(T,ω)和c2(T,ω),使得对∀t∈(0,T],有
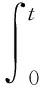
其中,xε(0)=Xε(0)+εη1(ω1),yε(0)=Yε(0)+εη2(ω2),zε(0)=Zε(0)+εη3(ω3)。
证明由O-U过程的连续性可知,对∀T>0,∃N(T,ω)>0,使得对∀t∈(0,T],成立:
(14)
由式(13)得到:
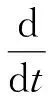
(15)
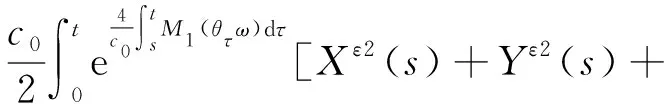
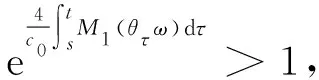
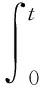
(16)
注意到Zε2(s)≤2(Zε(s)-r-σ)2+2(r+σ)2,故存在正常数c1(T,ω)和c2(T,ω),成立:
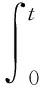
结果得证。
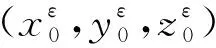
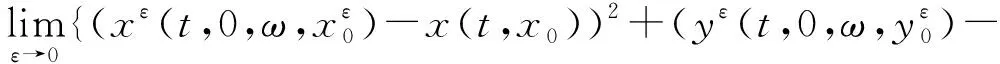
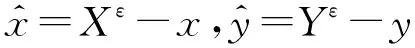
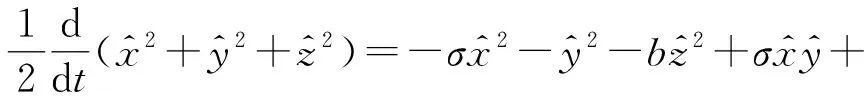
(17)
运用Young不等式,对式(17)右端各项分别估计,下面记c为通用常数,有
(18)
(19)
于是结合式(17)—式(19),令k0=max{2r2,2σ},则有
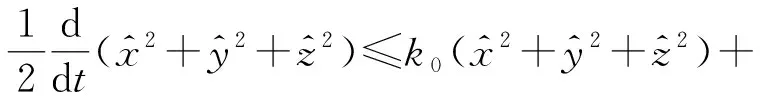
由此运用Gronwall引理得,有
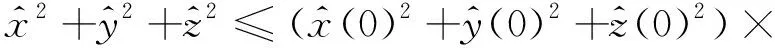
再次利用O-U过程的连续性,∃N1(T,ω),使得对t∈(0,T],M1(θtω)≤N1(T,ω),M2(θtω)≤N1(T,ω),由引理1的结果,可得:
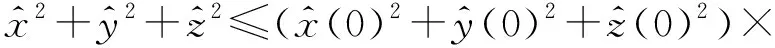
(20)
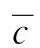
由式(20)可得:
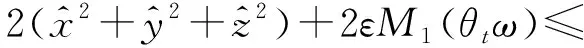
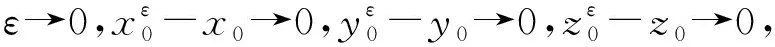
(xε(t)-x(t))2+(yε(t)-y(t))2+(zε(t)-z(t))2→0
从而引理2得证。
定理3 设{Aε(ω)}ω∈Ω是方程式(1)生成的随机动力系统φε的随机吸引子,A0是方程组式(1)当ε=0时所得的确定性动力系统φ0的全局吸引子,则对P-a.e.ω∈Ω成立,有
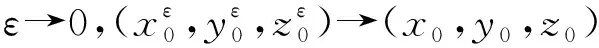
成立,根据引理1,有